Differential equation and solution

aka Pure and Warping Torsion

aka Free and Restrained Warping
ref: Hughes 6.1 (eqn 6.1.18)
the development of warping torsion up to this point was assumed to be "pure" or "free" i.e. it was the
only effect on a beam and it's behavior was unrestrained. this led us to state '' and ''' were constant.
the development of St. Venant's torsion in 13.10 was developed the same way, ' constant. we will now
address the situation where boundary conditions may affect one or both of these effects.
combined torsional resistance determined by:
M
x
= M
x
St_V
+ M
x
w M
x
St_V
is St. Venant's torsion = G K
T
'
M
x
w
is warping torsion = EI

'''
M
x
is internal or external concentrated torque T

M
x
= G K
T
' E I

'''
(1)

uniform (distributed) torque m
x
(torque per unit length) is related to Mx
equilibrium element => m
x
=
d
M
x
=>
dx
differentiating (1) =>
m
x
= E I

''' G K
T
''
(2)

solution of (1) has homogeneous and particular solution. rewriting:

G K
T
M
x let
2
=
G K
T
''' ' =

E I E I

E I

m x
homogeneous =>
'''
2
' = 0
assume solution
H
:= e
x

(
d
d
x
3
3

H

2

d
d
x

H
m
3
exp(mx)
2
mexp(mx)
=> m
3

2
m = m m
2

2
)
= 0
1
notes_16_pure_&_warping_torsion.mcd
I

x

x
I

A
roots
m := 0 m := m :=
0 x x
homogeneous solution =>

H
:= c
1
e + c
2
e + c
2
e
particular solution assume
P
:= A x
'''
G K
T
' =
M
x x

E I E I

d
3
3

P

2

P

2
A
is a solution <=> A :=
M
x
dx
dx

2
EI

2
A
M
x
E I

therefore:
x x
M
x
( ) := c
1
+ c
2
e + c
2
e + x
which can be rewritten as
x

2
EI

(x) := A + Bcosh
(
x
)
+ Csinh
(
x
)
+
M
x
x

2
EI

similarly equation (2) =>
IV

2
'' =
m
x
E I

homogeneous =>

IV

2
'' = 0
assume solution
H
:= e
m2 x
d
4
4

H

2

d
2
2

H
m2
4
exp(m2x)
2
m2
2
exp(m2x)
=> m2
4

2
m2
2
= 0
dx dx
roots
m2 := 0 m2 := 0 m2 := m2 :=
(double root)
0 0 x x
homogeneous solution =>

H
:= c
1
e + c
2
xe + c
3
e + c
4
e
particular solution assume
P
:= A1x
2
+ B x
3
B

d
4
4

P

2

d
2
2

P

2
(2 A1 + 6 Bx)
dx dx

2
(2 A1 + 6 Bx) =
m
x
is a solution <=> B := 0 and A1 :=
m
x

E I

2
2
EI

2
notes_16_pure_&_warping_torsion.mcd
x
I

A
m
x 2

P
:=
2
2
EI

x
d
d
x
4
4

P

2

d
d
x
2
2

m
x
check
E I

therefore:
x x
m
x 2

H
:= c
1
+ c
2
x + c
3
e + c
4
e x
which can be rewritten as
2
2
EI

x ( ) := A + Bx + Ccosh
(
x
)
+ Dsinh
(
x
)

m
x
x
2
2
2
EI

boundary conditions for various situations:
fixed end = 0
no twist
' = 0
no slope
pinned end = 0
no twist
Bi = 0
free warping
free end Bi = 0
free warping
''' = 0
no warping shear
continuous supports = 0
no twist

l'
=
r'
Bi
l
= Bi
r
continuous
transition point

l
=
r

l'
=
r'
Bi
l
= Bi
r
continuous
within span
general '' = 0
free end from bending
for a visual of Bi the bimoment see figure 6.13 in text
3
notes_16_pure_&_warping_torsion.mcd


A
Problem - Torsional response of Cantilever Girder
general solution for end
moment Mx and fixed at x =
0 (cantilever)
Vy=5000 lb
Mx
L
Vy=5000 lb
1/2 in
x
x 0 = ' = 0 =
x L '' := 0 =
from restrained_torsion.mcd
(x) := A + Bcosh
(
x
)
+ Csinh
(
x
)
+
M
x
x
M
x

2
EI

0 ( ) A + B = 0

2
E I

_pr x x ( ) :=
d
( ) _pr(x) Ccosh
(
x
)
+
M
x
dx

2
E I

' = 0
simplify
_pr 0 ( )
collect , C
C +
M
x
C +
M
x
= 0

2
E I

2
EI


or ... substituting
2
=
G K
T
C +
M
x
= 0
E I

G K
T

free end => '' = 0
d
2
_db_pr x x ( ) :=
dx
2
( )
_db_pr(x) Csinh
(
x
)

2
_db_pr(L) Csinh
(
L
)

2
Bcosh
(
L
)

2
+ Csinh
(
L
)

2
= 0
or .....
B + Ctanh
(
L
)
= 0
Given A + B = 0
C +
M
x
= 0 B + Ctanh
(
L
)
= 0
G K
T

|
M
x
tanh
(
L
)
|

G K
T |


M
x
|
Find(A, B , C)

G K
T
tanh
(
L
)
|
|
|

M
x |

G K
T
. \

4
notes_16_pure_&_warping_torsion.mcd
K
T T
C
K
T
K
T

T
T
B
B :=
M
x
tanh
(
L
)
C :=
M
x
K
T
GK
T
A := B
G K
(x) := A + Bcosh
(
x
)
+ Csinh
(
x
)
+
M
x
x

2
EI

x ( )
M
x
tanh
(
L
)
+
M
x
tanh
(
L
)
cosh
(
x
)

M
x
sinh
(
x
)
+
M
x
x
G K
T
G K
T
G K
T

2
E I

substituting for A, B, C, and ^2

x ( ) :=
M
x
tanh
(
L
)

(
cosh
(
x
)
1
)

M
x
sinh
(
x
)
+
M
x
x
GK
T
GK
T
G K
T
x ( ) :=
M
x

tanh
(
L
)

(
cosh
(
x
)
1
)
sinh
(
x
)
+ x
(
GK
T
d
x ( ) collect ,
M
x

(
tanh
(
L
)
sinh
(
x
)
cosh
(
x
)
+ 1
)
dx G K
T
_pr x ( ) :=
M
x

(
tanh
(
L
)
sinh
(
x
)
cosh
(
x
)
+ 1
)
G K
T

2
x
G K
T
d
2
( ) collect ,
M
x

(
tanh
(
L
)
cosh
(
x
)
sinh
(
x
))

dx

_db_pr x ( ) :=
M
x

(
tanh
(
L
)
cosh
(
x
)
sinh
(
x
))
G K K
T
3
x
G K
T
d
3
( ) collect ,
M
x

(
tanh
(
L
)
sinh
(
x
)
cosh
(
x
))

2
dx

_tr_pr x ( ) :=
M
x

(
tanh
(
L
)
sinh
(
x
)
cosh
(
x
))
G K K
T
let's look at these in general

2
=
G K
T

E I

5
notes_16_pure_&_warping_torsion.mcd
( ) , F2 x ( ) 2 < L < 5 F0(x) , F1 x ( ) , F3 x
L := 1 := 5 L = 5 x := 0, 0.1 .. L
above equations factoring out
M
x
F0(x) := tanh
(
L
)

(
cosh
(
x
)
1
)
sinh
(
x
)
+ x
G K
T

, (x) ~ total twist

M
x
F1(x) := tanh
(
L
)
sinh
(
x
)
cosh
(
x
)
+ 1
G K
T
, '(x) ~ St V torsion

M
x

F2(x) := tanh
(
L
)
cosh
(
x
)
sinh
(
x
)
G K
T
, ''(x) ~ axial stress warping torsion

M
x

2
F3(x) := tanh
(
L
)
sinh
(
x
)
cosh
(
x
)
G K
T
, '''(x) ~ shear stress warping torsion

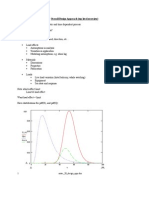
F0 x ( )
F1 x ( )
F2 x ( )
F3 x ( )
respectively
5
4
3
2
1
0
1
0 0.2 0.4 0.6 0.8
x
L
total twist
St. V torsion
axial stress - warping torsion
shear stress - warping torsion
6
notes_16_pure_&_warping_torsion.mcd