Documente Academic
Documente Profesional
Documente Cultură
S 1 Bassw 0 Oo
Încărcat de
jayneil7736Descriere originală:
Titlu original
Drepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
S 1 Bassw 0 Oo
Încărcat de
jayneil7736Drepturi de autor:
Formate disponibile
Statistics 1
MEI, 29/05/07 1/6
The Binomial distribution
Chapter Assessment
1. A fair die is rolled five times. Find:
(i) The probability that there are no sixes, [2]
(ii) The probability that there are exactly two sixes, [3]
(iii) The probability that only the first and last rolls give a six. [2]
2. The discrete random variable X is such that X ~ B(10, 0.34). Calculate
(i) P(X = 3), [3]
(ii) P(X > 1), [3]
(iii) P(4 s X < 7), [4]
(iv) E(X). [1]
3. The probability that Annie hits the target with a shot is 0.28. Find the least
number of shots Annie must fire so that the probability of at least one successful
shot is greater than 0.99. [4]
4. The probability that a newborn baby is a boy is 0.52. What is the probability that
in a family of 6 children there are more girls than boys? [4]
5. A discrete random variable X is such that X ~ B(n, 0.4) and P(X > 1) = 0.8704.
Find n. [4]
6. Over a long period of time it has been found that 5% of the articles made by a
particular manufacturer have been defective.
A batch of 100 articles is checked by a quality control inspector.
(i) What is the expected number of defective articles? [1]
(ii) What is the probability that the inspector will find 3 or more defective
articles in the batch of 100 articles? [4]
A company taking delivery of a large batch of these articles uses the following
procedure in order to decide whether to accept the batch. The batch is accepted
if:
- A random sample of 10 articles from the batch contains fewer than 2
defective articles
OR
- If the sample of 10 articles contains exactly two defective articles, a
second random sample of 10 is found to contain no defective articles.
(iii) What is the probability that the company will reject the delivered batch? [8]
Statistics 1
MEI, 29/05/07 2/6
7. A multiple-choice test consists of 18 questions. For each question there are four
possible answers given, only one of which is correct. John does no revision for
this test so decides to choose the answer to each question randomly.
(i) What is the probability that he gets no questions correct? [2]
(ii) What is the probability that he gets three questions correct? [3]
(iii) If John gets only three questions correct, what is the probability that they are
the first three questions? [3]
(iv) What is the most likely number of questions that he gets right? [3]
(v) Students who get more than half the questions correct pass this test. What is
the probability that John passes? [3]
(vi) After the test John reckoned that, if he had done a little revision, there were
four questions which he would definitely have got correct and that he would
have been able to eliminate one of the wrong answers in each of the other 14
questions, before randomly guessing his answer. Show that with a little
revision his chances of passing would have been increased by a factor of
more than 50. [3]
Total 60 marks
Statistics 1
MEI, 29/05/07 3/6
Solutions to Chapter Assessment
1. Let X be the number of sixes obtained
X ~ B(5,
1
6
)
(i) P(X = 0)
5
5 3125
0.402
6 7776
| |
= = =
|
\ .
(3 s.f.)
(ii) P(X = 2)
2 3
5
2
1 5 5 4 1 125 625
C 0.161
6 6 1 2 36 216 3888
| | | |
= = = =
| |
\ . \ .
(3 s.f.)
(iii) Probability
1 5 5 5 1 125
0.0161
6 6 6 6 6 7776
= = = (3 s.f.)
2. X ~ B(10, 0.34)
(i) P(X = 3) ( ) ( )
( ) ( )
10 3 7
3
3 7
C 0.34 0.66
10 9 8
0.34 0.66
1 2 3
0.257 (3 s.f.)
=
=
=
(ii) P(X > 1)
9 10
1 P( 0) P( 1)
1 (0.66) 10(0.34)(0.66)
0.904 (3 s.f.)
X X = = =
=
=
(iii) P(4 s X < 7)
10 4 6 10 5 5 10 6 4
4 5 6
4 6 5 5
6 4
P( 4) P( 5) P( 6)
C (0.34) (0.66) C (0.34) (0.66) C (0.34) (0.66)
10 9 8 7 10 9 8 7 6
(0.34) (0.66) (0.34) (0.66)
1 2 3 4 1 2 3 4 5
10 9 8 7
(0.34) (0.66)
1 2 3 4
0.437 (3 s.f.)
X X X = = + = + =
= + +
= +
+
=
(iv) E(X) 10 0.34 3.4 np = = =
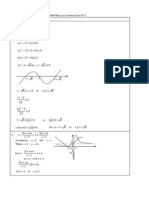
3. Let X be the number of successful shots.
X ~ B(n, 0.28)
Statistics 1
MEI, 29/05/07 4/6
P( 1) 0.99
1 P( 0) 0.99
P( 0) 0.01
(0.72) 0.01
n
X
X
X
> >
= >
= <
<
14 15
0.72 0.0101 and 0.72 0.00724 = =
So the least number of shots is 15.
4. Let X be the number of boys
X ~ B(6, 0.52)
There are more girls than boys if X = 0, 1 or 2.
Probability
6 5 2 4
P( 0) P( 1) P( 2)
6 5
(0.48) 6(0.52)(0.48) (0.52) (0.48)
1 2
0.307 (3 s.f.)
X X X = = + = + =
= + +
=
5. X B(n, 0.4)
( 1) 0.8704
1 P( 0) 0.8704
P( 0) 0.1296
0.6 0.1296
4
n
P X
X
X
n
> =
= =
= =
=
=
6. X ~ B(100, 0.05)
(i) E(X) 100 0.05 5 np = = =
(ii) P(X 3) 1 P( 2)
1 P( 0) P( 1) P( 2)
X
X X X
= s
= = = =
99 98 100 2
100 99
1 (0.95) 100 0.05(0.95) (0.05) (0.95)
1 2
0.882 (3 s.f.)
=
(iii) Let Y be the number of defective articles in a sample of 10
Y ~ B(10, 0.05)
P(Y = 0)
10
0.95 =
P(Y = 1)
9
10 0.05 0.95 =
P(Y = 2)
2 8 2 8
10 9
0.05 0.95 45 0.05 0.95
1 2
= =
Trial and improvement
used, but logs could
be used instead
Trial and improvement
used, but logs could
be used instead
Statistics 1
MEI, 29/05/07 5/6
P(fewer than 2 defective articles)
9 10
0.95 10 0.05 0.95
0.91386
= +
=
P(2 defective articles in 1st sample; no defective articles in second sample)
( )
2 8 10
45 0.05 0.95 0.95
0.04469
=
=
P(rejecting batch) 1 0.91386 0.04469
0.0415 (3 s.f.)
=
=
7. Let X be the number of questions John gets correct.
X ~ B(18, 0.25)
(i) P(X = 0)
18
0.75 0.00564 = =
(ii) P(X = 3)
18 3 15
3
3 15
(0.25) (0.75)
18 17 16
(0.25) (0.75)
1 2 3
0.170 (3 s.f.)
C =
=
=
(iii) Number of ways of choosing three questions from 18
18
3
18 17 16
C 816
1 2 3
= = =
Probability that those chosen are first three
1
0.00123
816
= = (3 s.f.)
(iv) E(X) 18 0.25 4.5 = =
P(X = 4)
4 14
18 17 16 15
(0.25) (0.75) 0.213
1 2 3 4
= =
P(X = 5)
5 13
18 17 16 15 14
(0.25) (0.75) 0.199
1 2 3 4 5
= =
The most likely outcome is that he will get 4 questions right.
(v) P(passing) = P(X > 9)
P(X = 10)
10 8
18 17 16 15 14 13 12 11
(0.25) (0.75)
1 2 3 4 5 6 7 8
=
P(X = 11)
11 7
18 17 16 15 14 13 12
(0.25) (0.75)
1 2 3 4 5 6 7
=
P(X = 12)
12 6
18 17 16 15 14 13
(0.25) (0.75)
1 2 3 4 5 6
=
P(X = 13)
13 5
18 17 16 15 14
(0.25) (0.75)
1 2 3 4 5
=
P(X = 14)
14 4
18 17 16 15
(0.25) (0.75)
1 2 3 4
=
Statistics 1
MEI, 29/05/07 6/6
P(X = 15)
15 3
18 17 16
(0.25) (0.75)
1 2 3
=
P(X = 16)
16 2
18 17
(0.25) (0.75)
1 2
P(X = 17)
17 1
18(0.25) (0.75) =
P(X = 18)
18
(0.25) =
P(passing)= 0.00542 (3 s.f.)
(vi) For the other 14 questions, let Y be the number of right answers.
Y ~ B(14,
1
3
)
To pass, at least 6 of these 14 questions must be correct.
P(Y = 0)
14
2
3
| |
=
|
\ .
P(Y = 1)
13
1 2
14
3 3
| || |
=
| |
\ .\ .
P(Y = 2)
2 12
14 13 1 2
1 2 3 3
| | | |
=
| |
\ . \ .
P(Y = 3)
3 11
14 13 12 1 2
1 2 3 3 3
| | | |
=
| |
\ . \ .
P(Y = 4)
4 10
14 13 12 11 1 2
1 2 3 4 3 3
| | | |
=
| |
\ . \ .
P(Y = 5)
5 9
14 13 12 11 10 1 2
1 2 3 4 5 3 3
| | | |
=
| |
\ . \ .
P(passing) = 1 0.690 = 0.310 (3 s.f.)
0.310
57.2
0.00542
=
so chances of passing have been increased by a factor of more than 50.
Using tables is
much quicker, if
this has been
covered
Again, quicker to
use tables
S-ar putea să vă placă și
- Using The Binomial Distribution - Solutions PDFDocument3 paginiUsing The Binomial Distribution - Solutions PDFwolfretonmathsÎncă nu există evaluări
- BFBFDGHDDocument3 paginiBFBFDGHDGabriel VasquezÎncă nu există evaluări
- IJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document8 paginiIJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongÎncă nu există evaluări
- JJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument9 paginiJJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongÎncă nu există evaluări
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document10 paginiMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongÎncă nu există evaluări
- RVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 paginiRVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongÎncă nu există evaluări
- HCI 2008 Promo W SolutionDocument12 paginiHCI 2008 Promo W SolutionMichael CheeÎncă nu există evaluări
- 2009 NYJC H2 Maths PromoDocument6 pagini2009 NYJC H2 Maths PromoSapphireansÎncă nu există evaluări
- TPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 paginiTPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongÎncă nu există evaluări
- TPJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument13 paginiTPJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongÎncă nu există evaluări
- AJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 paginiAJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongÎncă nu există evaluări
- Nyjc H2 Math P2Document6 paginiNyjc H2 Math P2jimmytanlimlongÎncă nu există evaluări
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document22 paginiMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongÎncă nu există evaluări
- Ajc H2 Math P1Document6 paginiAjc H2 Math P1jimmytanlimlongÎncă nu există evaluări
- VJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 paginiVJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongÎncă nu există evaluări
- 2014 - DHS - Prelim Paper 2Document7 pagini2014 - DHS - Prelim Paper 2Ng Shu QingÎncă nu există evaluări
- ACJC Maths Promos 2005Document3 paginiACJC Maths Promos 2005Suphadetch LeungÎncă nu există evaluări
- CJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument5 paginiCJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongÎncă nu există evaluări
- 2010 AJC Paper 2Document5 pagini2010 AJC Paper 2Fang Wen LimÎncă nu există evaluări
- RVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 paginiRVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongÎncă nu există evaluări
- TPJC Promo 2008Document11 paginiTPJC Promo 2008MathathleteÎncă nu există evaluări
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 paginiNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongÎncă nu există evaluări
- Math 2009 Promos SolutionsDocument8 paginiMath 2009 Promos SolutionsMichael CheeÎncă nu există evaluări
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document11 paginiMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongÎncă nu există evaluări
- TJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument12 paginiTJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongÎncă nu există evaluări
- RI JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 paginiRI JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongÎncă nu există evaluări
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1Document8 paginiMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1jimmytanlimlongÎncă nu există evaluări
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2Document15 paginiSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2jimmytanlimlongÎncă nu există evaluări
- IE101 Problem SetDocument6 paginiIE101 Problem SetGray Fiore FullbusterÎncă nu există evaluări
- PJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document7 paginiPJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlong0% (1)
- AJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document3 paginiAJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongÎncă nu există evaluări
- Maths in Focus Worked Solutions Yr 11 Adv Ch6Document135 paginiMaths in Focus Worked Solutions Yr 11 Adv Ch6LuoÎncă nu există evaluări
- 2006 AJC H2 MY SolnDocument9 pagini2006 AJC H2 MY Solnjunie9201Încă nu există evaluări
- 2012 ACJC Prelim H2 Math SolnDocument15 pagini2012 ACJC Prelim H2 Math Solnckhowh_23284524667% (3)
- JJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 paginiJJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongÎncă nu există evaluări
- VJC 2015 H2 J1 Math Promos Questions Singapore JC VictoriaDocument5 paginiVJC 2015 H2 J1 Math Promos Questions Singapore JC VictoriaAlxÎncă nu există evaluări
- ACJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 paginiACJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongÎncă nu există evaluări
- ACJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument6 paginiACJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongÎncă nu există evaluări
- NJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument10 paginiNJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongÎncă nu există evaluări
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document7 paginiNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongÎncă nu există evaluări
- Maths in Focus Worked Solutions Yr 11 Adv Ch8Document111 paginiMaths in Focus Worked Solutions Yr 11 Adv Ch8LuoÎncă nu există evaluări
- VJC JC1 H2 Maths 2015 Promo QuestionDocument5 paginiVJC JC1 H2 Maths 2015 Promo QuestionGM MonsterEtaÎncă nu există evaluări
- 2008 Promo 1Document15 pagini2008 Promo 1shinkir0Încă nu există evaluări
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document5 paginiNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongÎncă nu există evaluări
- Nyjc h2 Math p2 SolutionDocument11 paginiNyjc h2 Math p2 SolutionjimmytanlimlongÎncă nu există evaluări
- Ri h2 Math p2 SolutionsDocument11 paginiRi h2 Math p2 SolutionsjimmytanlimlongÎncă nu există evaluări
- PJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document10 paginiPJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongÎncă nu există evaluări
- Dhs Jc1 h2 Maths 2012 Promo SolutionsDocument13 paginiDhs Jc1 h2 Maths 2012 Promo SolutionsRyan LeeÎncă nu există evaluări
- 2013 HCI C1 Block Test H2 Mathematics Revision Package SolutionsDocument80 pagini2013 HCI C1 Block Test H2 Mathematics Revision Package SolutionsGabriel Francis ChuaÎncă nu există evaluări
- HW12Key PDFDocument3 paginiHW12Key PDFNursila OmarÎncă nu există evaluări
- TJC h2 Math p1 SolutionDocument12 paginiTJC h2 Math p1 SolutionjimmytanlimlongÎncă nu există evaluări
- Nyjc - 2007 Jc1 h2 Promo p2 - AnswerDocument12 paginiNyjc - 2007 Jc1 h2 Promo p2 - AnswerSudibyo GunawanÎncă nu există evaluări
- 2009 NJC SH2 H2 Mathematics Prelim Paper 2 SolutionsDocument21 pagini2009 NJC SH2 H2 Mathematics Prelim Paper 2 SolutionsNicholas ChoyÎncă nu există evaluări
- GCSE Maths - EquationsDocument50 paginiGCSE Maths - EquationsPrinceShalomÎncă nu există evaluări
- 635 - 2011-Exponential Equations - Explanation PracticeDocument3 pagini635 - 2011-Exponential Equations - Explanation Practiceapi-258903855Încă nu există evaluări
- Encoded Problems (StatsFinals)Document4 paginiEncoded Problems (StatsFinals)HueyÎncă nu există evaluări
- Discrete Probability DistributionDocument9 paginiDiscrete Probability DistributionabdulbasitÎncă nu există evaluări
- 21 Binomial Distribbution 13 14Document7 pagini21 Binomial Distribbution 13 14Ramchandra MurthyÎncă nu există evaluări
- Applied Statistical and Probability For EngineeringDocument45 paginiApplied Statistical and Probability For EngineeringYuling wangÎncă nu există evaluări
- STA 1380 - Fall 15 - Ch. 2 Practice SolutionsDocument10 paginiSTA 1380 - Fall 15 - Ch. 2 Practice SolutionstheapguyÎncă nu există evaluări
- Math 131Document1 paginăMath 131azizaldebasi1Încă nu există evaluări
- 1 Slide IS 310 - Business StatisticsDocument29 pagini1 Slide IS 310 - Business StatisticsSweet EmmeÎncă nu există evaluări
- Chapter 2 Commonly Used Probability DistributionDocument50 paginiChapter 2 Commonly Used Probability DistributionMohd NajibÎncă nu există evaluări
- Probability Models PDFDocument42 paginiProbability Models PDFBhaktaÎncă nu există evaluări
- 1 Solution PDFDocument6 pagini1 Solution PDFTooba MukhtarÎncă nu există evaluări
- UNIT I - Random VariablesDocument12 paginiUNIT I - Random VariablesShubham VishnoiÎncă nu există evaluări
- Ruin TheoryDocument29 paginiRuin TheoryAnonymous M8Bvu4FExÎncă nu există evaluări
- Bivariate Extreme Statistics, Ii: Authors: Miguel de CarvalhoDocument25 paginiBivariate Extreme Statistics, Ii: Authors: Miguel de CarvalhoDamon SÎncă nu există evaluări
- Chapter 4. Part 4: October 4, 2021Document19 paginiChapter 4. Part 4: October 4, 2021Ly Duc Hung (K15 HL)Încă nu există evaluări
- General Insurance 2Document35 paginiGeneral Insurance 2Evelyn PriscillaÎncă nu există evaluări
- Tut Sheet7Document2 paginiTut Sheet7Ekta SharmaÎncă nu există evaluări
- Stat. W2D1Document7 paginiStat. W2D1Sung Shin Woong-ill CiprianoÎncă nu există evaluări
- Exponential PDFDocument5 paginiExponential PDFChai Min HiungÎncă nu există evaluări
- Chapter-6-Random Variables & Probability DistributionsDocument13 paginiChapter-6-Random Variables & Probability DistributionsKebede HaileÎncă nu există evaluări
- C4a - Worksheet 6 - KeyDocument2 paginiC4a - Worksheet 6 - KeyMaria Charity Flores OrañoÎncă nu există evaluări
- Discrete and Continuous Random VariablesDocument8 paginiDiscrete and Continuous Random VariablesNurfajria NauliÎncă nu există evaluări
- Statistics and Probability ReviewerDocument6 paginiStatistics and Probability ReviewerJoseph Cabailo75% (8)
- Risk and UncertainityDocument11 paginiRisk and UncertainityKarthi BharathiÎncă nu există evaluări
- Lind16e PrefaceDocument28 paginiLind16e PrefacehfredianÎncă nu există evaluări
- Assignment CTCT 1Document2 paginiAssignment CTCT 1Smit MajithiaÎncă nu există evaluări
- EEN - 321 Digital Communications: Dr. Omer Mohsin Mubarak Assistant ProfessorDocument32 paginiEEN - 321 Digital Communications: Dr. Omer Mohsin Mubarak Assistant ProfessorMuhammad QasimÎncă nu există evaluări
- Qa Probability WBDocument5 paginiQa Probability WBChirag ChadhaÎncă nu există evaluări
- 2.1 List The Elements of Each of The Following Sample SpacesDocument7 pagini2.1 List The Elements of Each of The Following Sample SpacesSanjay dwi0% (1)
- Statistics: Review Notes Melissa E. Agulto, Ph.D. Professor, Central Luzon State UniversityDocument23 paginiStatistics: Review Notes Melissa E. Agulto, Ph.D. Professor, Central Luzon State UniversityMarjun CaguayÎncă nu există evaluări
- Full Download Essentials of Probability Statistics For Engineers Scientists 1st Edition Walpole Solutions ManualDocument36 paginiFull Download Essentials of Probability Statistics For Engineers Scientists 1st Edition Walpole Solutions Manuallibra.mimejx90w100% (33)
- Imprecise Probability in Risk Analysis (PDFDrive) PDFDocument48 paginiImprecise Probability in Risk Analysis (PDFDrive) PDFBabak Esmailzadeh HakimiÎncă nu există evaluări
- Probability S3Document32 paginiProbability S3anuragÎncă nu există evaluări
- Decision TheoryDocument12 paginiDecision TheoryFarish AhamedÎncă nu există evaluări
- Session 1 Basic Concepts and Principles in Statistics and Probability-Part 2Document31 paginiSession 1 Basic Concepts and Principles in Statistics and Probability-Part 2EDDIE T. PEREZÎncă nu există evaluări
- Bayesian Networks: 6.825 Techniques in Artificial IntelligenceDocument97 paginiBayesian Networks: 6.825 Techniques in Artificial IntelligenceVamsee GoruÎncă nu există evaluări