375

Gamma and Beta

Functions
THE GAMMA FUNCTION
The gamma function may be regarded as a generalization of n! (n-factorial), where n is any positive
integer to x!, where x is any real number. (With limited exceptions, the discussion that follows will be
restricted to positive real numbers.) Such an extension does not seem reasonable, yet, in certain ways,
the gamma function dened by the improper integral
x

1
0
t
x1
e
t
dt 1
meets the challenge. This integral has proved valuable in applications. However, because it cannot be
represented through elementary functions, establishment of its properties take some eort. Some of the
important ones are outlined below.
The gamma function is convergent for x > 0. (See Problem 12.18, Chapter 12.)
The fundamental property
x 1 xx 2
may be obtained by employing the technique of integration by
parts to (1). The process is carried out in Problem 15.1.
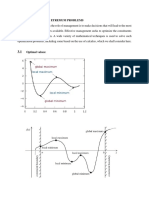
From the form (2) the function x can be evaluated for all
x > 0 when its values in the interval 1 % x < 2 are known.
(Any other interval of unit length will suce.) The table and
graph in Fig. 15-1 illustrates this idea.
TABLES OF VALUES AND GRAPH OF THE GAMMA
FUNCTION
n n
1.00 1.0000
1.10 0.9514
1.20 0.9182
1.30 0.8975
5
4
3
2
1
_
1
_
2
_
3
_
4
_
5
_
5
_
4
_
3
_
2
_
1 1 2 3 4 5
n
(n)
Fig. 15-1
Copyright 2002, 1963 by The McGraw-Hill Companies, Inc. Click Here for Terms of Use.
1.40 0.8873
1.50 0.8862
1.60 0.8935
1.70 0.9086
1.80 0.9314
1.90 0.9618
2.00 1.0000
The equation (2) is a recurrence relationship that leads to the factorial concept. First observe that if
x 1, then (1) can be evaluated, and in particular,
1 1:
From (2)
x 1 xx xx 1x 1 xx 1x 2 x kx k
If x n, where n is a positive integer, then
n 1 nn 1n 2 . . . 1 n! 3
If x is a real number, then x! x 1 is dened by x 1. The value of this identication is in
intuitive guidance.
If the recurrence relation (2) is characterized as a dierential equation, then the denition of x
can be extended to negative real numbers by a process called analytic continuation. The key idea is that
even though x is dened in (1) is not convergent for x < 0, the relation x
1
x
x 1 allows the
meaning to be extended to the interval 1 < x < 0, and from there to 2 < x < 1, and so on. A
general development of this concept is beyond the scope of this presentation; however, some information
is presented in Problem 15.7.
The factorial notion guides us to information about x 1 in more than one way. In the
eighteenth century, Sterling introduced the formula (for positive integer values n)
lim
n!1

2
p
n
n1
e
n
n!
1 4
This is called Sterlings formula and it indicates that n! asymptotically approaches

2
p
n
n1
e
n
for large
values of n. This information has proved useful, since n! is dicult to calculate for large values of n.
There is another consequence of Sterlings formula. It suggests the possibility that for suciently
large values of x,
x! x 1 %

2
p
x
x1
e
x
5a
(An argument supporting this is made in Problem 15.20.)
It is known that x 1 satises the inequality

2
p
x
x1
e
x
< x 1 <

2
p
x
x1
e
x
e
1
12x1
5b
Since the factor e
1
12x1
!0 for large values of x, the suggested value (5a) of x 1 is consistent
with (5b).
An exact representation of x 1 is suggested by the following manipulation of n!. (It depends on
n k! k n!.)
n! lim
k!1
12 . . . nn 1 n 2 . . . n k
n 1n 2 . . . n k
lim
k!1
k! k
n
n 1 . . . n k
lim
k!1
k 1k 2 . . . k n
k
n
:
Since n is xed the second limit is one, therefore, n! lim
k!1
k! k
n
n 1 . . . n k
: (This must be read as an
innite product.)
376 GAMMA AND BETA FUNCTIONS [CHAP. 15
This factorial representation for positive integers suggests the possibility that
x 1 x! lim
k!1
k! k
x
x 1 . . . x k
x 6 1; 2; k 6
Gauss veried this identication back in the nineteenth century.
This innite product is symbolized by x; k, i.e., x; k
k! k
x
x 1 x k
. It is called Gausss
function and through this symbolism,
x 1 lim
k!1
x; k 7
The expression for
1
x
(which has some advantage in developing the derivative of x) results as
follows. Put (6a) in the form
lim
k!1
k
x
1 x1 x=2 . . . 1 x=k
x 6
1
2
;
1
3
; . . . ;
1
k
Next, introduce

k
1
1
2

1
3

1
k
ln k
Then
lim
k!1

k
is Eulers constant. This constant has been calculated to many places, a few of which are
% 0:57721566 . . . .
By letting k
x
e
xln k
e
x
k
11=21=k
, the representation (6) can be further modied so that
x 1 e
x
lim
k!1
e
x
1 x
e
x=2
1 x=2

e
x=k
1 x=k
e
x
Y
1
k1
e
x
e
xln k
= 1
x
k

Y
1
1
k
x
k!k x lim
k!1
1 2 3 k
x 1x 2 x k
x
x
lim
k!1
x; k 8
Since x 1 xx;
1
x
xe
x
lim
k!1
1 x
e
x
1 x=2
e
x=2

1 x=k
e
x=k
xe
x
Y
1
1
1 x=k e
x=k
9
Another result of special interest emanates from a comparison of x1 x with the famous
formula
x
sin x
lim
k!1
1
1 x
2
1
1 x=2
2

1
1 x=k
2
& '

Y
1
1
f1 x=k
2
g 10
(See Dierential and Integral Calculus, by R. Courant (translated by E. J. McShane), Blackie & Son
Limited.)
1 x is obtained from y
1
y
y 1 by letting y x, i.e.,
x
1
x
1 x or 1 x xx
CHAP. 15] GAMMA AND BETA FUNCTIONS 377
Now use (8) to produce
x1 x
x
1
e
x
lim
k!1
Y
1
1
1 x=k
1
e
x=k
( ) !
e
x
lim
k!1
Y
1
1
1 x=k
1
e
x=k
!

1
x
lim
k!1
Y
1
1
1 x=k
2

Thus
x1 x

sin x
; 0 < x < 1 11a
Observe that (11) yields the result

1
2

p
11b
Another exact representation of x 1 is
x 1

2
p
x
x1
e
x
1
1
12x

1
288x
2

139
51840x
3

& '
12
The method of obtaining this result is closely related to Sterlings asymptotic series for the gamma
function. (See Problem 15.20 and Problem 15.74.)
The duplication formula
2
2x1
x x
1
2

p
2x 13a
also is part of the literature. Its proof is given in Problem 15.24.
The duplication formula is a special case m 2 of the following product formula:
x x
1
m

x
2
m

X
m1
m

m
1
2
mx
2
m1
2
mx 13b
It can be shown that the gamma function has continuous derivatives of all orders. They are
obtained by dierentiating (with respect to the parameter) under the integral sign.
It helps to recall that x

1
0
t
x1
e
yt
dt and that if y t
x1
, then ln y ln t
x1
x 1 ln t.
Therefore,
1
y
y
0
ln t.
It follows that

0
x

1
0
t
x1
e
t
ln t dt: 14a
This result can be obtained (after making assumptions about the interchange of dierentiation with
limits) by taking the logarithm of both sides of (9) and then dierentiating.
In particular,

0
1 is Eulers constant.) 14b
It also may be shown that

0
x
x

1
1

1
x

1
2

1
x 1


1
n

1
x n 1

15
(See Problem 15.73 for further information.)
THE BETA FUNCTION
The beta function is a two-parameter composition of gamma functions that has been useful enough in
application to gain its own name. Its denition is
378 GAMMA AND BETA FUNCTIONS [CHAP. 15
CHAP. 15] GAMMA AND BETA FUNCTIONS 379
Bx. y

1
0
t
x1
1 t
y1
dt 16
If x ! 1 and y ! 1, this is a proper integral. If x > 0. y > 0 and either or both x - 1 or y - 1, the
integral is improper but convergent.
It is shown in Problem 15.11 that the beta function can be expressed through gamma functions in the
following way
Bx. y
x y
x y
17
Many integrals can be expressed through beta and gamma functions. Two of special interest are

,2
0
sin
2x1
cos
2y1
d
1
2
Bx. y
1
2
x y
x y
18

1
0
x
p1
1 x
dx p p 1

sin p
0 - p - 1 19
See Problem 15.17. Also see Page 377 where a classical reference is given. Finally, see Chapter 16,
Problem 16.38 where an elegant complex variable resolution of the integral is presented.
DIRICHLET INTEGRALS
If V denotes the closed region in the rst octant bounded by the surface
x
a

p

y
b

q

z
c

r
1 and
the coordinate planes, then if all the constants are positive,

V
x
o1
y
[1
z
,1
dx dy dz
a
o
b
[
c
,
pqr

o
p

[
q

,
r

1
o
p

[
q

,
r
20
Integrals of this type are called Dirichlet integrals and are often useful in evaluating multiple
integrals (see Problem 15.21).
Solved Problems
THE GAMMA FUNCTION
15.1. Prove: (a) x 1 xx. x > 0; b n 1 n!. n 1. 2. 3. . . . .
a v 1

1
0
x
v
e
x
dx lim
M!1

M
0
x
v
e
x
dx
lim
M!1
x
v
e
x
j
M
0

M
0
e
x
vx
v1
dx
& '
lim
M!1
M
v
e
M
v

M
0
x
v1
e
x
dx
& '
vv if v > 0
b 1

1
0
e
x
dx lim
M!1

M
0
e
x
dx lim
M!1
1 e
M
1.
Put n 1. 2. 3. . . . in n 1 nn. Then
2 11 1. 3 22 2 1 2!. 4 33 3 2! 3!
In general, n 1 n! if n is a positive integer.
15.2. Evaluate each of the following.
a
6
23

5!
2 2!

5 4 3 2
2 2
30
b

5
2

1
2

3
2

3
2

1
2

3
2

1
2

1
2

1
2

3
4
c
3 2:5
5:5

2!1:50:5 0:5
4:53:52:51:50:5 0:5

16
315
d
6
8
3

5
2
3

6
5
3

2
3

2
3

5
2
3

4
3
15.3. Evaluate each integral.
a

1
0
x
3
e
x
dx 4 3! 6
b

1
0
x
6
e
2x
dx: Let 2x 7. Then the integral becomes

1
0
y
2

6
e
y
dy
2

1
2
7

1
0
y
6
e
y
dy
7
2
7

6!
2
7

45
8
15.4. Prove that
1
2

p
.

1
2

1
0
x
1=2
e
x
dx. Letting x u
2
this integral becomes
2

1
0
e
u
2
du 2

p
2

p
using Problem 12.31, Chapter 12
This result also is described in equation (11a,b) earlier in the chapter.
15.5. Evaluate each integral.
a

1
0

y
p
e
y
2
dy. Letting y
3
x, the integral becomes

1
0

x
1=3
p
e
x

1
3
x
2=3
dx
1
3

1
0
x
1=2
e
x
dx
1
3

1
2

p
3
b

1
0
3
4x
2
dx

1
0
e
ln3

4x
2

dz

1
0
e
4 ln 3z
2
dz. Let 4 ln 3z
2
x and the integral becomes

1
0
e
x
d
x
1=2

4 ln3
p
!

1
2

4 ln3
p

1
0
x
1=2
e
x
dx
1=2
2

4 ln3
p

p
4

ln 3
p
(c)

1
0
dx

lnx
p : Let ln x u. Then x e
u
. When x 1; u 0; when x 0; u 1. The integral
becomes

1
0
e
u

u
p du

1
0
u
1=2
e
u
du 1=2

p
15.6. Evaluate

1
0
x
m
e
ax
n
dx where m; n; a are positive constants.
380 GAMMA AND BETA FUNCTIONS [CHAP. 15
Letting ax
n
y, the integral becomes
_
1
0
y
a
_ _
1=n
_ _
m
e
y
d
y
a
_ _
1=n
_ _

1
na
m1=n
_
1
0
y
m1=n1
e
y
dy
1
na
m1=n

m1
n
_ _
15.7. Evaluate (a) 1=2; b 5=2.
We use the generalization to negative values dened by x
x 1
x
.
a Letting x
1
2
; 1=2
1=2
1=2
2

p
:
b Letting x 3=2; 3=2
1=2
3=2

2

p
3=2

4

p
3
; using a:
Then 5=2
3=2
5=2

8
15

p
:
15.8. Prove that
_
1
0
x
m
ln x
n
dx
1
n
n!
m1
n1
, where n is a positive integer and m > 1.
Letting x e
y
, the integral becomes 1
n
_
1
0
y
n
e
m1y
dy. If m1y u, this last integral becomes
1
n
_
1
0
u
n
m1
n
e
u
du
m1

1
n
m1
n1
_
1
0
u
n
e
u
du
1
n
m1
n1
n 1
1
n
n!
m1
n1
Compare with Problem 8.50, Chapter 8, page 203.
15.9. A particle is attracted toward a xed point O with a force inversely proportional to its instanta-
neous distance from O. If the particle is released from rest, nd the time for it to reach O.
At time t 0 let the particle be located on the x-axis at x a > 0 and let O be the origin. Then by
Newtons law
m
d
2
x
dt
2

k
x
1
where m is the mass of the particle and k > 0 is a constant of proportionality.
Let
dx
dt
v, the velocity of the particle. Then
d
2
x
dt
2

dv
dt

dv
dx

dx
dt
v
dv
dx
and (1) becomes
mv
dv
dx

k
x
or
mv
2
2
k lnx c 2
upon integrating. Since v 0 at x a, we nd c k lna. Then
mv
2
2
k ln
a
x
or v
dx
dt

2k
m
_

ln
a
x
_
3
where the negative sign is chosen since x is decreasing as t increases. We thus nd that the time T taken for
the particle to go from x a to x 0 is given by
T

m
2k
_
_
a
0
dx

lna=x
_ 4
CHAP. 15] GAMMA AND BETA FUNCTIONS 381
Letting lna=x u or x ae
u
, this becomes
T a

m
2k
r

1
0
u
1=2
e
u
du a

m
2k
r

1
2
a

m
2k
r
THE BETA FUNCTION
15.10. Prove that (a) Bu; v Bv; u; b Bu; v 2

=2
0
sin
2u1
cos
2v1
d.
(a) Using the transformation x 1 y, we have
Bu; v

1
0
x
u1
1 x
v1
dx

1
0
1 y
u1
y
v1
dy

1
0
y
v1
1 y
u1
dy Bv; u
(b) Using the transformation x sin
2
, we have
Bu; v

1
0
x
u1
1 x
v1
dx

=2
0
sin
2

u1
cos
2

v1
2 sin cos d
2

=2
0
sin
2u1
cos
2v1
d
15.11. Prove that Bu; v
u v
u v
u; v > 0.
Letting z
2
x
2
; we have u

1
0
z
u1
e
z
dx 2

1
0
x
2u1
e
x
2
dx:
Similarly, v 2

1
0
y
2v1
e
y
2
dy: Then
u v 4

1
0
x
2u1
e
x
2
dx

1
0
y
2v1
e
y
2
dy

4

1
0

1
0
x
2u1
y
2v1
e
x
2
y
2

dx dy
Transforming to polar coordiantes, x cos ; y sin,
u v 4

=2
0

1
0

2uv1
e

2
cos
2u1
sin
2v1
d d
4

1
0

2uv1
e

2
d

=2
0
cos
2u1
sin
2v1
d

2u v

=2
0
cos
2u1
sin
2v1
d u v Bv; u
u v Bu; v
using the results of Problem 15.10. Hence, the required result follows.
The above argument can be made rigorous by using a limiting procedure as in Problem 12.31,
Chapter 12.
15.12. Evaluate each of the following integrals.
a

1
0
x
4
1 x
3
dx B5; 4
5 4
9

4!3!
8!

1
280
382 GAMMA AND BETA FUNCTIONS [CHAP. 15
b

2
0
x
2
dx

2 x
p : Letting x 2v; the integral becomes
4

2
p

1
0
v
2

1 v
p dv 4

2
p

1
0
v
2
1 v
1=2
dv 4

2
p
B3;
1
2

4

2
p
3 1=2
7=2

64

2
p
15
c

a
0
y
4

a
2
y
2
q
dy: Letting y
2
a
2
x or y

x
p
; the integral becomes
a
6

1
0
x
3=2
1 x
1=2
dx a
6
B5=2; 3=2
a
6
5=2 3=2
4

a
6
16
15.13. Show that

=2
0
sin
2u1
cos
2v1
d
u v
2 u v
u; v > 0.
This follows at once from Problems 15.10 and 15.11.
15.14. Evaluate (a)

=2
0
sin
6
d; b

=2
0
sin
4
cos
5
d; c

0
cos
4
d.
a Let 2u 1 6; 2v 1 0; i.e., u 7=2; v 1=2; in Problem 15.13:
Then the required integral has the value
7=2 1=2
2 4

5
32
:
b Letting 2u 1 4; 2v 1 5; the required integral has the value
5=2 3
2 11=2

8
315
:
c The given integral 2

=2
0
cos
4
d:
Thus letting 2u 1 0; 2v 1 4 in Problem 15.13, the value is
2 1=2 5=2
2 3

3
8
.
15.15. Prove

=2
0
sin
p
d

=2
0
cos
p
d a
1 3 5 p 1
2 4 6 p

2
if p is an even positive integer,
(b)
2 4 6 p 1
1 3 5 p
is p is an odd positive integer.
From Problem 15.13 with 2u 1 p; 2v 1 0, we have

=2
0
sin
p
d

1
2
p 1
1
2

2
1
2
p 2
(a) If p 2r, the integral equals
r
1
2

1
2

2 r 1

r
1
2
r
3
2

1
2

1
2

1
2

2rr 1 1

2r 12r 3 1
2r2r 2 2

2

1 3 5 2r 1
2 4 6 2r

2
(b) If p 2r 1, the integral equals
r 1
1
2

2 r
3
2

rr 1 1

p
2r
1
2
r
1
2

1
2

p
2 4 6 2r
1 3 5 2r 1
In both cases

=2
0
sin
p
d

=2
0
cos
p
d, as seen by letting =2 .
CHAP. 15] GAMMA AND BETA FUNCTIONS 383
15.16. Evaluate (a)

=2
0
cos
6
d; b

=2
0
sin
3
cos
2
d; c

2
0
sin
8
d.
(a) From Problem 15.15 the integral equals
1 3 5
2 4 6

5
32
[compare Problem 15.14(a)].
(b) The integral equals

=2
0
sin
3
1 sin
2
d

=2
0
sin
3
d

=2
0
sin
5
d
2
1 3

2 4
1 3 5

2
15
The method of Problem 15.14(b) can also be used.
c The given integral equals 4

=2
0
sin
8
d 4
1 3 5 7
2 4 6 8

35
64
:
15.17. Given

1
0
x
p1
1 x
dx

sin p
, show that p 1 p

sin p
, where 0 < p < 1.
Letting
x
1 x
y or x
y
1 y
, the given integral becomes

1
0
y
p1
1 y
p
dy B p; 1 p p 1 p
and the result follows.
15.18. Evaluate

1
0
dy
1 y
4
.
Let y
4
x. Then the integral becomes
1
4

1
0
x
3=4
1 x
dx

4 sin=4

2
p
4
by Problem 15.17 with p
1
4
.
The result can also be obtained by letting y
2
tan .
15.19. Show that

2
0
x

8 x
3
3
p
dx
16
9

3
p .
Letting x
3
8y or x 2y
1=3
, the integral comes

1
0
2y
1=3

81 y
3
p

2
3
y
2=3
dy
8
3

1
0
y
1=3
1 y
1=3
dy
8
3
B
2
3
;
4
3

8
3

2
3

4
3

2

8
9

1
3

2
3

8
9

sin =3

16
9

3
p
STIRLINGS FORMULA
15.20. Show that for large positive integers n; n!

2n
p
n
n
e
n
approximately.
By denition z

1
0
t
z1
e
t
dt. Let lfz x 1 then
x 1

1
0
t
x
e
t
dt

1
0
e
tlnt
x
dt

1
0
e
tx lnt
dt 1
For a xed value of x the function x ln t t has a relative maximum for t x (as is demonstrated by
elementary ideas of calculus). The substutition t x y yields
x 1 e
x

1
x
e
xlnxyy
dy x
x
e
x

1
x
e
x ln1
y
x
y
dy 2
384 GAMMA AND BETA FUNCTIONS [CHAP. 15
To this point the analysis has been rigorous. The following formal steps can be made rigorous by
incorporating appropriate limiting procedures; however, because of the diculty of the proofs, they shall be
omitted.
In (2) introduce the logarithmic expansion
ln 1
y
x

y
x

y
2
2x
2

y
3
3x
3
3
and also let
y

x
p
v; dy

x
p
dv
Then
x 1 x
x
e
x

x
p

1
x
e
v
2
=2v
3
=3

x
p

dv 4
For large values of x
x 1 % x
x
e
x

x
p

1
x
e
v
2
=2
dv x
x
e
x

2x
p
When x is replaced by integer values n, then the Stirling relation
n! x 1 %

2x
p
x
x
e
x
5
is obtained.
It is of interest that from (4) we can also obtain the result (12) on Page 378. See Problem 15.72.
DIRICHLET INTEGRALS
15.21. Evaluate I

V
x
1
y
1
z
1
dx dy dz where V is
the region in the rst octant bounded by the sphere
x
2
y
2
z
2
1 and the coordinate planes.
Let x
2
u; y
2
v; z
2
w. Then
I

r
u
1=2
v
1=2
w
1=2
du
2

u
p
dv
2

v
p
dw
2

w
p

1
8

r
u
=21
v
=21
w
=21
du dv dw 1
where r is the region in the uvw space bounded by the plane
u v w 1 and the uv; vw, and uw planes as in Fig. 15-2.
Thus,
I
1
8

1
u0

1u
v0

1uv
w0
u
=21
v
=21
w
=21
du dv dw 2

1
4

1
u0

1u
v0
u
=21
v
=21
1 u v
=2
du dv

1
4

1
u0
u
=21

1u
v0
v
=21
1 u v
=2
dv
& '
du
Letting v 1 ut, we have

1u
v0
v
=21
1 u v
=2
dv 1 u
=2

1
t0
t
=21
1 t
=2
dt
1 u
=2
=2 =2 1
=2 1
CHAP. 15] GAMMA AND BETA FUNCTIONS 385
Fig. 15-2
so that (2) becomes
I
1
4
=2 =2 1
=2 1

1
u0
u
=21
1 u
=2
du 3

1
4
=2 =2 1
=2 1

=2 =2 1
=2 1

=2 =2 =2
8 =2 1
where we have used =2 =2 =2 1.
The integral evaluated here is a special case of the Dirichlet integral (20), Page 379. The general case
can be evaluated similarly.
15.22. Find the mass of the region bounded by x
2
y
2
z
2
a
2
if the density is x
2
y
2
z
2
.
The required mass 8

V
x
2
y
2
z
2
dx dy dz, where V is the region in the rst octant bounded by the
sphere x
2
y
2
z
2
a
2
and the coordinate planes.
In the Dirichlet integral (20), Page 379, let b c a; p q r 2 and 3. Then the
required result is
8
a
3
a
3
a
3
2 2 2
3=2 3=2 3=2
1 3=2 3=2 3=2

4s
9
945
MISCELLANEOUS PROBLEMS
15.23. Show that

1
0

1 x
4
p
dx
f1:4g
2
6

2
p .
Let x
4
y. Then the integral becomes
1
4

1
0
y
3=4
1 y
1=2
dy
1
4
1=4 3=2
7=4

p
6
f1=4g
2
1:4 3=4
From Problem 15.17 with p 1=4; 1=4 3=4

2
p
so that the required result follows.
15.24. Prove the duplication formula 2
2p1
p p
1
2

p
2p.
Let I

=2
0
sin
2p
x dx; J

=2
0
sin
2p
2xdx.
Then I
1
2
B p
1
2
;
1
2

p
1
2

p
2 p 1
Letting 2x u, we nd
J
1
2

0
sin
2p
u du

=2
0
sin
2p
u du I
J

=2
0
2 sinx cos x
2p
dx 2
2p

=2
0
sin
2p
x cos
2p
x dx But
2
2p1
B p
1
2
; p
1
2

2
2p1
f p
1
2
g
2
2p 1
Then since I J,
p
1
2

p
2p p

2
2p1
f p
1
2
g
2
2p 2p
386 GAMMA AND BETA FUNCTIONS [CHAP. 15
and the required result follows. (See Problem 15.74, where the duplication formula is developed for the
simpler case of integers.)
15.25. Show that

=2
0
d

1
1
2
sin
2

q
f1=4g
2
4

p .
Consider
I

=2
0
d

cos
p

=2
0
cos
1=2
d
1
2
B
1
4
;
1
2

1
4

p
2
3
4

f
1
4
g
2
2

2
p
as in Problem 15.23.
But I

=2
0
d

cos
p

=2
0
d

cos
2
=2 sin
2
=2
p

=2
0
d

1 2 sin
2
=2
p :
Letting

2
p
sin=2 sin in this last integral, it becomes

2
p

=2
0
d

1
1
2
sin
2

q , from which the result

follows.
15.26. Prove that

1
0
cos x
x
p
dx

2 p cos p=2
; 0 < p < 1.
We have
1
x
p

1
p

1
0
u
p1
e
xu
du. Then

1
0
cos x
x
p
dx
1
p

1
0

1
0
u
p1
e
xu
cos x du dx

1
p

1
0
u
p
1 u
2
du 1
where we have reversed the order of integration and used Problem 12.22, Chapter 12.
Letting u
2
v in the last integral, we have by Problem 15.17

1
0
u
p
1 u
2
du
1
2

1
0
v
p1=2
1 v
dv

2 sin p 1=2

2 cos p=2
2
Substitution of (2) in (1) yields the required result.
15.27. Evaluate

1
0
cos x
2
dx.
Letting x
2
y, the integral becomes
1
2

1
0
cos y

y
p dy
1
2

2
1
2
cos =4
!

1
2

=2
p
by Problem 15.26.
This integral and the corresponding one for the sine [see Problem 15.68(a)] are called Fresnel integrals.
Supplementary Problems
THE GAMMA FUNCTION
15.28. Evaluate (a)
7
2 4 3
; b
3 3=2
9=2
; c 1=2 3=2 5=2.
Ans. a 30; b 16=105; c
3
8

3=2
CHAP. 15] GAMMA AND BETA FUNCTIONS 387
15.29. Evaluate (a)

1
0
x
4
e
x
dx; b

1
0
x
6
e
3x
dx; c

1
0
x
2
e
2x
2
dx:
Ans. a 24; b
80
243
; c

2
p
16
15.30. Find (a)

1
0
e
x
2
dx; b

1
0

x
4
p
e

x
p
dx; c

1
0
y
3
e
2y
5
dy.
Ans. a
1
3

1
3
; b
3

p
2
; c
4=5
5

16
5
p
15.31. Show that

1
0
e
st

t
p dt

8
r
; s > 0.
15.32. Prove that v

1
0
ln
1
x

v1
dx; v > 0.
15.33. Evaluate (a)

1
0
lnx
4
dx; b

1
0
x lnx
3
dx; c

1
0

ln1=x
3
p
dx.
Ans: a 24; b 3=128; c
1
3

1
3

15.34. Evaluate (a) 7=2; b 1=3. Ans: a 16

p
=105; b 3 2=3
15.35. Prove that lim
x!m
x 1 where m 0; 1; 2; 3; . . .
15.36. Prove that if m is a positive interger, m
1
2

1
m
2
m

p
1 3 5 2m 1
15.37. Prove that
0
1

1
0
e
x
ln xdx is a negative number (it is equal to , where 0:577215 . . . is called
Eulers constant as in Problem 11.49, Page 296).
THE BETA FUNCTION
15.38. Evaluate (a) B3; 5; b B3=2; 2; c B1=3; 2=3: Ans: a 1=105; b 4=15; c 2=

3
p
15.39. Find (a)

1
0
x
2
1 x
3
dx; b

1
0

1 x=x
p
dx; c

2
0
4 x
2

3=2
dx.
Ans: a 1=60; b =2; c 3
15.40. Evaluate (a)

4
0
u
3=2
4 u
5=2
du; b

3
0
dx

3x x
2
p : Ans: a 12; b
15.41. Prove that

a
0
dy

a
4
y
4
p
f1=4g
2
4a

2
p :
15.42. Evaluate (a)

=2
0
sin
4
cos
4
d; b

2
0
cos
6
d: Ans: a 3=256; b 5=8
15.43. Evaluate (a)

0
sin
5
d; b

=2
0
cos
5
sin
2
d: Ans: a 16=15; b 8=105
15.44. Prove that

=2
0

tan
p
d =

2
p
.
388 GAMMA AND BETA FUNCTIONS [CHAP. 15
15.45. Prove that (a)

1
0
xdx
1 x
6


3

3
p ; b

1
0
y
2
dy
1 y
4


2

2
p .
15.46. Prove that

1
1
e
2x
ae
3x
b
dx
2
3

3
p
a
2=3
b
1=3
where a; b > 0.
15.47. Prove that

1
1
e
2x
e
3x
1
dx
2
9

3
p
[Hint: Dierentiate with respect to b in Problem 15.46.]
15.48. Use the method of Problem 12.31, Chapter 12, to justify the procedure used in Problem 15.11.
DIRICHLET INTEGRALS
15.49. Find the mass of the region in the xy plane bounded by x y 1; x 0; y 0 if the density is

xy
p
.
Ans: =24
15.50. Find the mass of the region bounded by the ellipsoid
x
2
a
2

y
2
b
2

z
2
c
2
1 if the density varies as the square of
the distance from its center.
Ans:
abck
30
a
2
b
2
c
2
; k constant of proportionality
15.51. Find the volume of the region bounded by x
2=3
y
2=3
z
2=3
1.
Ans: 4=35
15.52. Find the centroid of the region in the rst octant bounded by x
2=3
y
2=3
z
2=3
1.
Ans: " xx " yy " zz 21=128
15.53. Show that the volume of the region bounded by x
m
y
m
z
m
a
m
, where m > 0, is given by
8f1=mg
3
3m
2
3=m
a
3
.
15.54. Show that the centroid of the region in the rst octant bounded by x
m
y
m
z
m
a
m
, where m > 0, is given
by
" xx " yy " zz
3 2=m 3=m
4 1=m 4=m
a
MISCELLANEOUS PROBLEMS
15.55. Prove that

b
a
x a
p
b x
q
dx b a
pq1
B p 1; q 1 where p > 1; q > 1 and b > a.
[Hint: Let x a b ay:]
15.56. Evaluate (a)

3
1
dx

x 13 x
p ; b

7
3

7 xx 3
4
p
dx.
Ans: a ; b
2 f1=4g
2
3

p
15.57. Show that
f1=3g
2
1=6

p

2
3
p

3
p .
15.58. Prove that Bu; v
1
2

1
0
x
u1
x
v1
1 x
uv
dx where u; v > 0.
[Hint: Let y x=1 x:
CHAP. 15] GAMMA AND BETA FUNCTIONS 389
15.59. If 0 < p < 1 prove that

=2
0
tan
p
d

2
sec
p
2
.
15.60. Prove that

1
0
x
u1
1 x
v1
x r
uv

Bu; v
r
u
1 r
uv
where u; v, and r are positive constants.
[Hint: Let x r 1y=r y.]
15.61. Prove that

=2
0
sin
2u1
cos
2v1
d
a sin
2
b cos
2

uv

Bu; v
2a
v
b
u
where u; v > 0.
[Hint: Let x sin
2
in Problem 15.60 and choose r appropriately.]
15.62. Prove that

1
0
dx
x
x

1
1
1

1
2
2

1
3
3

15.63. Prove that for m 2; 3; 4; . . .
sin

m
sin
2
m
sin
3
m
sin
m1
m

m
2
m1
[Hint: Use the factored form x
m
1 x 1x
1
x
2
x
n1
, divide both sides by x 1, and
consider the limit as x !1.]
15.64. Prove that

=2
0
ln sinx dx =2 ln 2 using Problem 15.63.
[Hint: Take logarithms of the result in Problem 15.63 and write the limit as m !1 as a denite integral.]
15.65. Prove that
1
m

2
m

3
m


m1
m

2
m1=2

m
p :
[Hint: Square the left hand side and use Problem 15.63 and equation (11a), Page 378.]
15.66. Prove that

1
0
ln x dx
1
2
ln2.
[Hint: Take logarithms of the result in Problem 15.65 and let m !1.]
15.67. (a) Prove that

1
0
sinx
x
p
dx

2 p sin p=2
; 0 < p < 1.
(b) Discuss the cases p 0 and p 1.
15.68. Evaluate (a)

1
0
sin x
2
dx; b

1
0
x cos x
3
dx.
Ans: a
1
2

=2
p
; b

3

3
p
1=3
15.69. Prove that

1
0
x
p1
lnx
1 x
dx
2
csc pcot p; 0 < p < 1.
15.70. Show that

1
0
ln x
x
4
1
dx

2

2
p
16
.
15.71. If a > 0; b > 0, and 4ac > b
2
, prove that

1
1

1
1
e
ax
2
bxycy
2

dxdy
2

4ac b
2
p
390 GAMMA AND BETA FUNCTIONS [CHAP. 15
15.72. Obtain (12) on Page 378 from the result (4) of Problem 15.20.
[Hint: Expand e
v
3
=3

n
p

in a power series and replace the lower limit of the integral by 1.]
15.73. Obtain the result (15) on Page 378.
[Hint: Observe that x
1
x
x !, thus ln x lnx 1 lnx, and

0
x
x

0
x 1
x 1

1
x
Furthermore, according to (6) page 377.
x ! lim
k!1
k! k
x
x 1 x k
Now take the logarithm of this expression and then dierentiate. Also recall the denition of the Euler
constant, .
15.74. The duplication formula (13a) Page 378 is proved in Problem 15.24. For further insight, develop it for
positive integers, i.e., show that
2
2n1
n
1
2
n 2n

p
Hint: Recall that
1
2
, then show that
n
1
2

2n 1
2

2n 1 5 3 1
2
n

p
:
Observe that
2n 1
2
n
n 1

2n!
2
n
n!
2n 1 5 3 1
Now substitute and rene.
CHAP. 15] GAMMA AND BETA FUNCTIONS 391