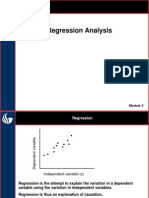
Section 4.1 is the intercept of this line and is the slope.

This equation is the linear

regression model with a single regressor, in which Y is the dependent variable and X is the independent variable or the regressor. is the population regression line or the population regression function. If you knew the value of X, according to this population regression line, you would be able to predict that the value of dependent variable Y is . The intercept line. The slope and the slope are the coefficients of the population

regression line, also known as the parameters of the population regression is the change in Y associated with a unit change in X. The intercept is the value of the population regression line when X=0. Sometimes, this intercept does not provide real-world meaning such as in STR example; it would be the predicted value of test scores when there are no students in the class. ui is the error term which includes every other factors beside X that determine Y for a specific observation, i.

Section 4.2 The OLS estimator chooses the regression coefficients so that the estimated regression line is as close as possible to the observed data, where closeness is measured by the sum of the squared mistakes made in predicting Y given X. As discussed in Section 3.1, the sample average, , is the least squares estimator of the population mean E(Y); that is, minimizes the total squared estimation mistakes minimize that: when m = among all possible estimators m. In order to

=> Solving for the final equation for m shows that .

The OLS estimator extends this idea to the linear regression model from . The sum of the squared prediction mistakes over all n observations is:

Where b0 and b1 are the estimators of

and

, respectively. These and .

estimators are called the ordinary least squares (OLS) estimators of The OLS estimators of the slope and intercept are: The OLS regression line:

The predicted value of Yi given Xi based on OLS regression line: The residual for the ith observation:

Section 4.3 A) Measures of Fit

Explained sum of squares (ESS): Total sum of squares (TSS):

Sum of squared residuals (variance of Yi NOT explained by Xi) (SSR): Regression R2 = (ranges between 0 and 1 and measures the

fraction of the variance of Yi that is explained by Xi) The R2 of the regression of Y on the single regressor X is the square of the correlation coefficient between X and Y. TSS = ESS + SSR If then Xi explains none of the variation of Yi and the predicted value of Yi based on the regression is just the sample average of Yi. In this case, the ESS is 0 and SSR = TSS; thus, the R2 is 0. Conversely, if Xi explains all of the variation of Yi then Yi = i for all every residual and i is 0 so that ESS = TSS and R2 = 1. => R2 near 0 means Xi is not very good at predicting Yi and vice versa. B) The standard error of the regression (SER) SER is an estimator of the standard deviation of the regression error ui. The units of ui and Yi are the same so SER is a measure of the spread of the observations around the regression line, measured in the units of the dependent variable. The SER is computed using OLS residuals:

Also, the sample average of the OLS residuals is 0. The reason to use n-2 is the same as the reason to use n-1, that is, to correct the slight downward bias introduced because two regression coefficients were estimated.

High SER means there is a large spread of scatterplot around the regression line as measured in points of the test. That also means the prediction of test scores using only STR will often be wrong by a large amount. Low R2 (and large SER) does not, by itself, imply that this regression is good or bad but it does tell that there is other important factors influence test scores.