Right triangle definitions

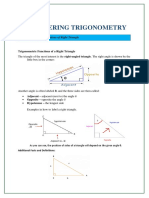
A right triangle always includes a 90 (/2 radians) angle, here labeled C. Angles A and B may vary. Trigonometric functions specify the relationships among side lengths and interior angles of a right triangle.

All of the trigonometric functions of an angle can be constructed geometrically in terms of a unit circle centered at O. In order to define the trigonometric functions for the angle A, start with an arbitrary right triangle that contains the angle A: We use the following names for the sides of the triangle:

The hypotenuse is the side opposite the right angle, or defined as the longest side of a right-angled triangle, in this case h. The opposite side is the side opposite to the angle we are interested in, in this case a. The adjacent side is the side that is in contact with the angle we are interested in and the right angle, hence its name. In this case the adjacent side is b.

All triangles are taken to exist in the Euclidean plane so that the inside angles of each triangle sum to radians (or 180); therefore, for a right triangle the two non-right angles are between zero and /2 radians (or 90). The reader should note that the following

definitions, strictly speaking, only define the trigonometric functions for angles in this range. We extend them to the full set of real arguments by using the unit circle, or by requiring certain symmetries and that they be periodic functions. 1) The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case

. Note that this ratio does not depend on the particular right triangle chosen, as long as it contains the angle A, since all those triangles are similar. The set of zeroes of sine (i.e., the values of x for which sinx = 0) is . 2) The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In our case

. The set of zeros of cosine is

. 3) The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. In our case

. The set of zeroes of tangent is . The same set of the sine function since

. The remaining three functions are best defined using the above three functions. 4) The cosecant csc(A) is the multiplicative inverse of sin(A), i.e. the ratio of the length of the hypotenuse to the length of the opposite side:

. 5) The secant sec(A) is the multiplicative inverse of cos(A), i.e. the ratio of the length of the hypotenuse to the length of the adjacent side:

. 6) The cotangent cot(A) is the multiplicative inverse of tan(A), i.e. the ratio of the length of the adjacent side to the length of the opposite side:

[edit] Mnemonics
There are a number of mnemonics for the above definitions; for example, SOHCAHTOA (sounds like "soak a toe-a" or "sock-a toe-a"). It means: SOH sin = opposite/hypotenuse

CAH cos = adjacent/hypotenuse

TOA tan = opposite/adjacent. This can also be remembered as rhymes such as "Some Old Hippie Caught Another Hippie Trippin' On Acid or; "Some Old Hags Can't Always Hide Their Old Age" with the initials, in triplets, forming the ratios for sine, cosine, and tangent, respectively.

[edit] Slope definitions

Equivalent to the right-triangle definitions, the trigonometric functions can be defined in terms of the rise, run, and slope of a line segment relative to some horizontal line. The slope is commonly taught as "rise over run" or rise/run. The three main trigonometric functions are commonly taught in the order sine, cosine, tangent. With a unit circle, the following correspondense of definitions exists: 1. Sine is first, rise is first. Sine takes an angle and tells the rise. 2. Cosine is second, run is second. Cosine takes an angle and tells the run. 3. Tangent is the slope formula that combines the rise and run. Tangent takes an angle and tells the slope. This shows the main use of tangent and arctangent: converting between the two ways of telling the slant of a line, i.e., angles and slopes. (Note that the arctangent or "inverse tangent" is not to be confused with the cotangent, which is cos divided by sin.) While the radius of the circle makes no difference for the slope (the slope doesn't depend on the length of the slanted line), it does affect rise and run. To adjust and find the actual rise and run, just multiply the sine and cosine by the radius. For instance, if the circle has radius 5, the run at an angle of 1 is 5 cos(1)