Ch04 Kinematics

Available At: mathcity.org Contact At: qadri86@yahoo.
com
M th

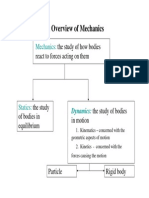
INTRODUCTION
The branch of mechanics which deals with the motion of object is called dynamics. It is
divided into two branches:
(i) Kinematics (ii) Kinetics
Kinematics:
The branch of dynamics which deals with geometry of motion of a body without any
reference of the force acting on the body is called kinematics.
Kinetics:
The branch of dynamics which deals with geometry of motion of a body with reference to the
force causing motion is called kinetics.
Points to be Remember
(i) The position of a particle can be specified by a vector r whose initial point is at the
origin of some fixed coordinate system and the terminal point is at the particle. This
vector is called position vector. If the particle is moving, the vector r changes with
time. i.e. it is a function of time.
(ii) The curve traced by a moving particle is called the trajectory or the path of the
particle.
(iii) The path of the particle can be specified by the vector equation
r r (t) ________ (i)
The path of the particle can also be specified by three scalar equations
x = x(t), y = y(t), z = z(t) __________ (ii)
These equations are obtained by equating the components of vectors on two sides of
the equation (i). Equation gives the coordinates of the points of the path for different
value s of t. We call these as parametric equations of the path.
CHAPTER
4
KINEMATICS

Available At: mathcity.org Contact At: qadri86@yahoo.com
2
Cartesian Components of Velocity & Acceleration

y

B dr
dt
= V

Q

r

r + r
P

r
A
x
O
Let AB be a part of the trajectory of the particle as shown in figure. Let the particle at time t
be at the point P whose position vector is r . After a small time t, let the particle reach the
point Q whose position vector is r + r . The PQ
= r is the displacement of the particle from

the point P in the small time interval t. The quotient
r
t

gives the average rate of change of displacement of the particle in the interval t. If we start
decreasing the time interval t, the displacement r will go on deceasing and the point Q gets
nearer and nearer to P. Thus
lim

r
t

can be considered as the instantaneous rate of change of displacement. This is defined as the
instantaneous velocity or the simply velocity v of the particle at point P.
Thus,
v lim

r
t
dr
dt

Proceeding in similar way we can see that the acceleration a (the instantaneous rate of change
of velocity) at time t is given by
a= lim
t 0
v
t
=
dv
dt
=
d
dt
dr
dt
=
d
2
r
dt
2

In Cartesian coordinates, we can write
r = xi
+ yi

Then
v =
d
dt
xi
+ yi
=
dx
dt
i
+
dy
dt
j

3
a =
d
2
dt
2
xi
+ yi
=
d
2
x
dt
2
i
+
d
2
y
dt
2
j

Thus
v
x
= x- component of velocity =
dx
dt

v
y
= y- component of velocity =
dy
dt

a
x
x- component of acceleration
d
2
x
dt
2

a
y
y- component of acceleration
d
2
y
dt
2

Question 1
A particle is moving in such a way that it position at any time t is specified by
r = t
3
+ t
2
i
+ cost + sin
2
tj
+ e
t
+ logtk

Find the velocity and acceleration.
Solution
If v and a are velocity and acceleration of particle respectively. Then
v
dr
dt
d
dt
t
3
+ t
2
i
+ cost + sin
2
tj
+ e
t
+ logtk

= 3t
2
+ 2ti
+ sint + 2sintcostj
+ e
t
+
1
t
k

= 3t
2
+ 2ti
+ sin2t sintj
+ e
t
+
1
t
k

and a
dv
dt

d
dt
3t
2
+ 2ti
+ sin2t sintj
+ e
t
+
1
t
k

6t + 2i
+ 2cos2t costj
+ e
t
1
t
2
k

Question 2
A particle P start from O at t = 0. Find tits velocity and acceleration of particle at any time t
if its position at that time is given by
r = at
2
i
+ 4atj

Solution
If v and a are velocity and acceleration of particle respectively. Then

4
v
dr
dt
d
dt
at
2
i
+ 4atj
= 2ati
+ 4aj

and a
dv
dt

d
dt
2ati
+ 4aj
2ai

Question 3
At any time t, the position of a particle moving in a plane can be specified by
(acoswt, asinwt) where a and w are constants. Find the component of its velocity and
acceleration along the coordinates axis.
Solution
Let r = acoswt i
+ asinwt j

Differentiate w.r.t t, we get
v = awsinwt i
+ awcoswt j

Differentiate again w.r.t t, we get
a = aw
2
coswt i
aw
2
sinwt j

Thus the component of velocity and acceleration are
v
x
= awsinwt , v
y
= awcoswt
a
x
= aw
2
coswt , a
y
= aw
2
sinwt
Question 4
The position of particle moving along an ellipse is given by r = acost i
+ bsint j
If a > b,
find the position of the particle where velocity has maximum and minimum magnitude.
Solution
As r = acost i
+ bsint j

v = asint i
+ bcost j

v = asint
2
+ bcost
2

=
a
2
sin
2
t + b
2
cos
2
t
= a
2
sin
2
t + b
2
1 sin
2
t
=
a
2
sin
2
t + b
2
b
2
sin
2
t
= sin
2
ta
2
b
2
+ b
2

5
v is maximum when sin
2
t is maximum. i.e. sin
2
t = 1 sint = 1 t = 90, 270
For t = 90
r = acos90 i
+ bsin90 j
= bj

For t = 270
r = acos270 i
+ bsin270 j
= bj

So the position of the particle when velocity has maximum magnitude is bj
.
v is minimum when sin
2
t is minimum. i.e. sin
2
t = 0 sint = 0 t = 0, 180
For t = 0
r = acos0 i
+ bsin0 j
= ai

For t = 180
r = acos180 i
+ bsin180 j
= ai

So the position of the particle when velocity has minimum magnitude is ai
.
Radial & Transverse Components of Velocity & Acceleration

In polar coordinates, the position of a particle is specified by a radius vector r and the polar
angle which are related to x and y through the relations
x = rcos
y = rsin

provided the two coordinates frames have the same origin and the xaxis and the initial line
coincide. The direction of radius vector is known as radial direction and that perpendicular
to it in the direction of increasing is called transverse direction.

y

s

P

r
90
0
+

x
O

6
Let r and s be units vectors in the radial and transverse direction respectively as shown in
figure. Then
r = cosi
+ sinj
______________ (i)
s = cos(90
0
+ )i
+ sin(90
0
+ )j
= sini
+ cosj
______________ (ii)
Differentiating (i) w.r.t t
dr
dt
d
dt
cosi
+ sinj

sin i
d
dt
+ cosj
d
dt

d
dt
sin i
+ cosj

d
dt
s By (ii) ______________ (iii)
Differentiating (ii) w.r.t t
ds
dt
d
dt
sini
+ cosj

cos i
d
dt
sinj
d
dt

d
dt
sin i
+ cosj

d
dt
r By (i) ______________ (iv)
We know that
r =
r
r
r = r r
Now v =
dr
dt

d
dt
rr
dr
dt
. r + r
dr
dt

dr
dt
. r + r
d
dt
s
Thus,
v
r
= Radial component of velocity =
dr
dt
= r
v

= Transverse component of velocity = r
d
dt
= r

Where dot denotes the differentiation with respect to time t.

7
Let a be the acceleration Then
a =
dv
dt

d
dt
dr
dt
. r + r
d
dt
s

d
dt
dr
dt
. r +
d
dt
r
d
dt
s
=
d
dt
dr
dt
r +
dr
dt
dr
dt
+
dr
dt
d
dt
s +
d
dt
d
dt
rs +
ds
dt
r
d
dt

=
d
2
r
dt
2
r +
dr
dt
dr
dt
+
dr
dt
d
dt
s +
d
2
dt
2
rs +
ds
dt
d
dt
r
=
d
2
r
dt
2
r +
dr
dt
d
dt
s +
dr
dt
d
dt
s +
d
2
dt
2
r s +
d
dt
r
d
dt
r By iii& (iv)
=
d
2
r
dt
2
r r
d
dt
2
r + 2
dr
dt
d
dt
s +
d
2
dt
2
r s
=
d
2
r
dt
2
r
d
dt
2
r + 2
dr
dt
d
dt
+
d
2
dt
2
r s
Thus,
a
r
= Radial component of acceleration =
d
2
r
dt
2
r
d
dt
2
= r r
2

a

= Transverse component of acceleration = 2
dr
dt
d
dt
+ r
d
2

dt
2
= 2r
+ r

Question 5
A particle P moves in a plane in such away that at any time t, its distance from point O is
r = at + bt
2
and the line connecting O and P makes an angle = ct
3/2
with a fixed line OA.
Find the radial and transverse components of velocity and acceleration of particle at t = 1
Solution
Given that
r = at + bt
2
and = ct
3/2

dr
dt
= a + 2bt and
d
dt
=
3
2
ct
1
2

Differentiate again w.r.t t, we get
d
2
r
dt
2
= 2b and
d
2
dt
2
=
3
4
ct
1
2

8
At t = 1
r = a + b and = c
dr
dt
= a + 2b ,
d
dt
=
3
2
c ,
d
2
r
dt
2
= 2b and
d
2
dt
2
=
3
4
c
Radial component of velocity = v
r
=
dr
dt
= a + 2b
Transverse component of velocity = v
= r
d
dt
=
3
2
ca + b
Radial component of acceleration = a
r
=
d
2
r
dt
2
r
d
dt
2

= 2b a + b
3
2
c
2

= 2b
9
4
c
2
a + b
=
1
4
8b 9c
2
a + b
Transverse component of acceleration = a
= 2
dr
dt
d
dt
+ r
d
2
dt
2

= 2a + 2b
3
2
c + a + b
3
4
c
=
3
4
c5a + 9b
Question 6
Find the radial and transverse components of velocity of a particle moving along the curve
ax
2
+ by
2
= 1
at any time t if the polar angle is = ct
2

Solution
Given that
= ct
2

d
dt
= 2ct
Also given that
ax
2
+ by
2
= 1
First we change this into polar form by putting x = rcos and y = rsin

9
ar
2
cos
2
+ br
2
sin
2
= 1
r
2
(acos
2
+ bsin
2
) = 1
racos
2
+ bsin
2
= 1
r = acos
2
+ bsin
2

dr
dt
=
1
2
acos
2
+ bsin
2

3
2
a2cossin
d
dt
+ b2sincos
d
dt

=
1
2
acos
2
+ bsin
2

3
2
a bsin2
d
dt

=
1
2
acos
2
+ bsin
2

3
2
a bsin2.2ct
=
cta bsin2
acos
2
+ bsin
2

3
2

Radial component of velocity =
dr
dt
=
cta bsin2
acos
2
+ bsin
2

3
2

Transverse component of velocity = r
d
dt
=
2ct
acos
2
+ bsin
2

1
2

Question 7
Find the radial and transverse components of acceleration of a particle moving along the
circle x
2
+ y
2
= a
2
with constant velocity c.
Solution
Given that
d
dt
= c
d
2
dt
2
= 0
Also given that
x
2
+ y
2
= a
2

First we change this into polar form by putting x = rcos and y = rsin
r
2
cos
2
+ r
2
sin
2
= a
2

r
2
(cos
2
+ sin
2
) = a
2

r
2
= a
2

10
r = a

dr
dt
= 0
d
2
r
dt
2
= 0
Radial component of acceleration = a
r
=
d
2
r
dt
2
r
d
dt
2

= 0 ac
2

= ac
2

Transverse component of acceleration = a
= 2
dr
dt
d
dt
+ r
d
2
dt
2

= 0
Tangential & Normal Components of Velocity & Acceleration

y

B
Tangent
Q

s

r

r + r
P

r
A
x
O
Let AB be a part of the trajectory of the particle as shown in figure. Let the particle at time t
be at the point P whose position vector is r . After a small time t, let the particle reach the
point Q whose position vector is r + r . Then PQ
= r and arcPQ = s
Now v =
dr
dt
=
dr
ds
.
ds
dt
= v.
dr
ds
_____________(i)
Here
dr
ds
is a unit tangent at point P.
Let t
be a unit vector along the tangent at P and n unit vector along normal at the point P.
Then
dr
ds
t

Using this in (i), we get

11
v = v t
+ 0.n
Thus,
v
t
= Tangential component of velocity = v
v
n
= Normal component of velocity = 0
Hence the velocity is along the tangent to the path.
y
Normal

Tangent
n

t

90
0

90
0
+

x
O
Let a be the acceleration. Then
a =
dv
dt

=
d
dt
v t

=
dv
dt
t
+ v
dt
dt

=
dv
dt
t
+ v
dt
d
d
ds
ds
dt

=
dv
dt
t
+ v
dt
d
(Kv)
ds
dt
v
Where
d
ds
= K is called curvature and K =
1

So a =
dv
dt
t
+ v
dt
d
.
v

=
dv
dt
t
+
v
2
dt
d

Since t
and n are unit vectors along tangent and normal at P Therefore

t
= cosi
+ sinj

n = cos(90
0
+ )i
+ sin(90
0
+ )j
= sini
+ cosj

Now
dt
d
d
cosi
+ sinj

sin i
+ cos j

12
n
So a =
dv
dt
t
+
v
2
n
Thus,
Tangential component of acceleration = a
t
=
dv
dt

Normal component of acceleration = a
n
=
v
2

Where
=
1 +
dy
dx
3
2
d
2
y
dx
2

Question 8
A particle is moving along the parabola x
2
= 4ay with constant speed. Determine tangential
and normal components of its acceleration when it reaches the point whose abscissa is 5a.
Solution
Given that
x
2
= 4ay
Differentiate w.r.t x, we get
2x = 4a
dy
dx

dy
dx
=
x
2a

Differentiate again w.r.t x, we get
d
2
y
dx
2
1
2a

Given that x = 5a therefore
dy
dx
=
5a
2a
=
5
2

We know that
=
1 +
dy
dx
3
2
d
2
y
dx
2
=
1 +
5
2
3
2
1
2a
= 2a 1 +
5
4
3
2
= 2a
9
4
3
2
= 2a
3
2
27a
4

Since the particle is moving with constant speed therefore
dv
dt
= 0

13
Tangential component of acceleration = a
t
=
dv
dt
0
n
=
v
2
=
v
2
27a
4
4v
2
27a

Question 9
Find the tangential and normal component of acceleration of a point describing ellipse
x
2
a
2
y
2
b
2
= 1
With uniform speed v when the particle is at (0, b).
Solution
Given that
x
2
a
2
y
2
b
2
= 1
x
2
b
2
+ y
2
a
2
= a
2
b
2

2b
2
x + 2a
2
y
dy
dx
= 0

dy
dx
=
b
2
x
a
2
y

d
2
y
dx
2

b
2
a
2
y x
dy
dx
y

b
2
a
2
y x
b
2
x
a
2
y

b
2
a
2
1
y
+
x
2
b
2
a
2
y
3

At (0, b)
dy
dx
=
b
2
0
a
2
b
= 0
and
d
2
y
dx
2

b
2
a
2
1
b
+
0.b
2
a
2
b
3

b
a
2

14
We know that
=
1 +
dy
dx
3
2
d
2
y
dx
2

=
1 + 0
2
3
2
b
a
2
=
a
2
b

Since the particle is moving with uniform speed therefore
dv
dt
= 0
Thus, Tangential component of acceleration = a
t
=
dv
dt
0
n
=
v
2
=
v
2
a
2
b
bv
2
a
2
\

Question 10
A particle is moving with uniform speed along the curve
x
2
y = a x
2
+
a
2
5

Show that acceleration has maximum value
10v
2
9a

Solution
Given that
x
2
y = a x
2
+
a
2
5

y = a +
a
3
5
x
2

dy
dx

2a
3
5
x
3

d
2
y
dx
2
6a
3
5
x
4

We know that

15
=
1 +
dy
dx
3
2
d
2
y
dx
2

=
1 +
2a
3
5
x
3
3
2
6a
3
5
x
4
=
1 +
4a
6
5x
6
3
2
6a
3
5x
4
=
5x
4
6a
3
5x
6
+ 4a
6
5x
6
3
2
=
5x
6
+ 4a
6
3
2
30a
3
x
5
____(i)
We know that
a =
dv
dt
t

v
2
n
Since the particle is moving with constant speed therefore
dv
dt
= 0
a =
v
2
n
|a| =
v
2
|n|
v
2
|n| = 1
|a| will maximum when is minimum.
Differentiate (i) w.r.t x, we get
d
dx
30a
3
x
5
3
2
5x
6
+ 4a
6
1
2
30x
5
5x
6
+ 4a
6
3
2
150a
3
x
4
30a
3
x
5

5x
6
+ 4a
6
1
2
30
a
6
x
10
30a
3
x
5
45x
5
5x
6
+ 4a
6
150a
3
x
4

5x
6
+ 4a
6
1
2
30a
3
x
6
45x
6
55x
6
+ 4a
6

5x
6
+ 4a
6
1
2
30a
3
x
6
45x
6
25x
6
20a
6

5x
6
+ 4a
6
1
2
30a
3
x
6
20x
6
20a
6

205x
6
+ 4a
6
1
2
30a
3
x
6
x
6
a
6

205x
6
+ 4a
6
1
2
30a
3
x
6
x
2
a
2
x
4
+ x
2
a
2
+ a
4

Putting
d
dx
= 0, we get
x = a
Since

16
d
dx
< 0 before x = a and
d
dx
> 0 after x = a
Therefore is minimum when x = a

Thus
min
=
5a
6
+ 4a
6
3
2
30a
3
a
5
=
9a
6
3
2
30a
8
=
27a
30
=
9
10
a
Maximum value of acceleration =
v
2
min
=
v
2
9
10
a
=
10v
2
9a

%%%%% End of The Chapter # 4 %%%%%

Ch04 Kinematics

Încărcat de

Informații document

Descriere originală:

Titlu original

Drepturi de autor

Formate disponibile

Partajați acest document

Partajați sau inserați document

Opțiuni de partajare

Vi se pare util acest document?

Este necorespunzător acest conținut?

Drepturi de autor:

Formate disponibile

Ch04 Kinematics

Încărcat de

Drepturi de autor:

Formate disponibile

Available At: mathcity.org Contact At: qadri86@yahoo.

= r is the displacement of the particle from

and n are unit vectors along tangent and normal at P Therefore

S-ar putea să vă placă și