T Schmitz

Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Modeling and analysis of nonlinear systems applied to a
guitar signal chain.
ABAV, Sart-Tilman, Feb 21
Schmitz Thomas
Department of Electrical Engineering and Computer Science,
University of Li`ege
20 fevrier 2014
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Communication Outline
Introduction to the guitar instrumentation problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker simulation
Objective evaluation of the model
Subjective evaluation of the model
Conclusion
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Section 1
Introduction to the guitar instrumentation problem
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Goals of the thesis
Figure: A guitar chain example Figure: Objective of the work
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Utility ?
Figure: Home studio ? Figure: Home studio !
Advantages of the simulation :

Wide variety of sounds and

timbres.

Weight and overcrowding.

Easier comparison between

two sounds.

Cheaper.
Disadvantages of the simulation :

Fidelity of the sound

accuracy of the model.

Psychologic :

An emulation still be an
emulation.

Numerical sounds is cooler

than analogical sound.
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Section 2
Non-linear modelling
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Non-linear modelisation : Black box approach
Figure: Guitar chain,in blue the non-linear elements
Figure: Nonlinears models
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Non-linear modelisation : Volterra Series
Relation between input x[n] and output y[n] for non-linear system
_
_
_
y[n] =
M

i =1
N

1
=0
...
N

i
=0
h
i
[
1
, ...,
i
] x[n
1
]... x[n
i
] (1)
Where h
i
[n] If the non-linearities are static, then
h
i
[
1
, ...,
i
] = 0
k
=
1
with k [1, i ].
Ex 2
th
Volterra kernel :
_
_
_
_
_
_
_
1 0 0 0 0
0 0.9 0 0 0
0 0 0.8 0 0
.
.
.
.
.
.
0 0.1
_
_
_
_
_
_
_
Eq (1) becomes :
y[n] = x[n] h
1
[n] + x[n]
2
h
2
[n] + ... + x[n]
M
h
M
[n] (2)
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Excitation signal
Figure: Impulse response
measurement.
We choose :
x(t) = Asin((t)) (3)
where the variable phase (t) grows ex-
ponentialy. This property allows us to
separate the dierents orders of distor-
sion as (for example) :
x
3
(t) =
A
3
4
[3 sin((t)) sin(3(t))]
(4)
We can show that it exist a link bet-
ween :
M.(t) (t +
M
) (5)
So that
x
3
(t)x
1
(t) (t)+(t +
3
) (6)
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Deconvolved signal
z[n] =y[n] x
1
[n]
=
_
x[n] h
1
[n] + x[n]
2
h
2
[n] + ... + x[n]
M
h
M
[n]
_
x
1
[n]
(7)
15 16 17 18 19 20 21
0.1
0.08
0.06
0.04
0.02
0
0.02
0.04
0.06
0.08
0.1
Time(s)
A
m
p
l
i
t
u
d
e
h3 h5 h4 h2 h1

3
=3.18s

2
=2.01s
Figure: Impulse response measurement. z(t) the deconvolved signal
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Connection between Volterra kernels h
i
and measured kernels
m
i
We have proved :
F(h
i
)
link
F(m
i
)
So that, we obtain ( > 0) :
F(h
i
) F(m
i
)
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
H
1
(w) =M
1
(w) + 3e
2jB
M
3
(w) + 5e
4jB
M
5
(w)
H
2
(w) =
2
A
je
jB
[M
2
(w) + 4e
2jB
M
4
(w)]
H
3
(w) =
4
A
2
e
2jB
[M
3
(w) + 5e
2jB
M
5
(w)]
H
4
(w) =
8
A
3
_
je
3jB
_
M
4
(w)
H
5
(w) =
16
A
4
M
5
(w)e
4jB
(8)
Where A takes into account of the amplitude of the emitted sine sweep and B
depends on the parameters of the chosen sweep
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Section 3
Non-linear loudspeaker simulation
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Comparison between the real and simulated signal
Figure: Simulation with 5 Volterra kernels
Figure: Simulation with 1 Volterra kernel
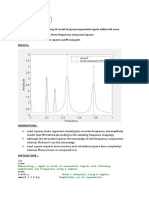
10
2
70
68
66
64
62
60
58
56
54
52
Frequency in Hz
A
m
p
l
i
t
u
d
e

d
b


H3v22Vrms
H3v19Vrms
H3v16Vrms
H3v13Vrms
Figure: H
3
(, Amplitude)
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Blind test with real chords guitar
0 vs 0 0 vs 1 0 vs 2
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
% of error
Sample 2 : Simulated
With 5 Volterra kernels
Compare sample 0 to samples 0, 1, 2
Sample 1 : Simulated
With 1 Volterra kernel
Sample 0 : Real
Figure: 82% of tested listener were not able to distinguish a simulation of type 2. 72%
of tested listener were not able to distinguish a simulation of type 1 and 22% of tested
listener hear a dierence where there were none !
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Section 4
Conclusion
T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Conclusion
Achievement

Non-linear loudspeaker modelisation based on Volterra series.

Subjective and objective evaluation of the model.

Future works

Improve simulation delity.

Solving the amplitude dependance of the model.

Try the model on more non-linear system.

T Schmitz
Introduction to the
guitar instrumentation
problem
Non-linear modelling
IR measurement
Model reconstruction
Non-linear loudspeaker
simulation
Objective evaluation
of the model
Subjective evaluation
of the model
Conclusion
Thank you for your attention !