Documente Academic
Documente Profesional
Documente Cultură
Saniga
Încărcat de
galaxy5111Descriere originală:
Drepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
Saniga
Încărcat de
galaxy5111Drepturi de autor:
Formate disponibile
GEOMETRY OF TWO-QUBITS
(ICS Praha, January 25, 2007)
METOD SANIGA
Astronomical Institute of the Slovak Academy of Sciences
SK-05960 Tatransk a Lomnica, Slovak Republic
(msaniga@astro.sk)
AN OVERVIEW OF THE TALK
1. Introduction
2. Projective Line Over P
1
(M
2
(GF(2)))
Recalling the Concept of a Projective Ring Line
Full Matrix Ring M
2
(GF(2))) and Its Subrings
P
1
(M
2
(GF(2)))
Specic Subconguration of P
1
(M
2
(GF(2)))
3. Geometry of Two-Qubits
9+6 and 10+5 Factorizations of the Algebra of Pauli Operators
The Two Factorizations in Terms of Sublines of P
1
(M
2
(GF(2)))
Generalized Quadrangle of Order Two, W(2)
The Two Factorizations in Terms of Geometric Hyperplanes of W(2)
Correspondence Between the Two Pictures
Generalizations for N-qubits
4. Conclusion/References
Joint work with Michel Planat (FEMTO-ST, Besan con, FR)
and Petr Pracna (JH-Inst, Prague, CZ)
1. Introduction
Projective lines dened over nite associative rings with unity/identity
have recently been recognized to be an important novel tool for getting
a deeper insight into the underlying algebraic geometrical structure of
nite dimensional quantum systems.
As per the two-qubit case, i.e., the set of 15 operators/generalized four-
by-four Pauli spin matrices, of particular importance turned out to be
the lines dened over the direct product of the simplest Galois elds,
GF(2) GF(2) . . . GF(2).
Here, the line dened over GF(2) GF(2) plays a prominent role in
grasping qualitatively the basic structure of so-called Mermin squares,
i. e., three-by-three arrays in certain remarkable 9 + 6 split-ups of the
algebra of operators (quant-ph/0603051, quant-ph/0603206), whereas
the line over GF(2)GF(2)GF(2) reects some of the basic features
of a specic 8 + 7 (cube-and-kernel) factorization of the set (quant-
ph/0605239).
Motivated by these partial ndings, we started our quest for such a ring
line that would provide us with a complete picture of the algebra of all
the 15 operators/matrices.
After examining a large number of lines dened over commutative rings
(math.AG/0605301, math.AG/0606500), we gradually realized that a
proper candidate is likely to be found in the non-commutative domain
and this, indeed, turned out to be a right move.
It is, as we shall demonstrate in what follows, the projective line dened
over the full two-by-two matrix ring with entries in GF(2), M
2
(GF(2))
the unique simple non-commutative ring of order 16 featuring six
units (invertible elements) and ten zero-divisors.
2. Projective Line Over P
1
(M
2
(GF(2)))
Recalling the Concept of a Projective Ring Line
Given
an associative ring R with unity/identity and
GL(2, R), the general linear group of invertible two-by-two matrices
with entries in R,
a pair (a, b) R
2
is called admissible over R if there exist c, d R such
that
_
_
_
a b
c d
_
_
_ GL(2, R). (1)
The projective line over R, usually denoted as P
1
(R), is the set of equiv-
alence classes of ordered pairs (a, b), where is a unit of R and (a, b)
is admissible. Two points X := (a, b) and Y := (c, d) of the line are
called distant or neighbor according as
_
_
_
a b
c d
_
_
_ GL(2, R) or
_
_
_
a b
c d
_
_
_ / GL(2, R), (2)
respectively. GL(2, R) has an important property of acting transitively
on a set of three pairwise distant points; that is, given any two triples of
mutually distant points there exists an element of GL(2, R) transforming
one triple into the other.
Full Matrix Ring M
2
(GF(2))) and Its Subrings
The projective line we are exclusively interested in here is the one dened
over the full two-by-two matrix ring with GF(2)-valued coecients, i. e.,
R = M
2
(GF(2))
_
_
_
_
_
_
_
_ | , , , GF(2)
_
_
. (3)
In an explicit form:
UNITS: Invertible matrices (i. e., matrices with non-zero determinant). They
are of two distinct kinds: those which square to 1,
1
_
_
_
1 0
0 1
_
_
_ , 2
_
_
_
0 1
1 0
_
_
_ , 9
_
_
_
1 1
0 1
_
_
_ , 11
_
_
_
1 0
1 1
_
_
_ , (4)
and those which square to each other,
12
_
_
_
0 1
1 1
_
_
_ , 13
_
_
_
1 1
1 0
_
_
_ . (5)
ZERO-DIVISORS: Matrices with vanishing determinant. These are also of
two dierent types: nilpotent, i. e. those which square to zero,
3
_
_
_
1 1
1 1
_
_
_ , 8
_
_
_
0 1
0 0
_
_
_ , 10
_
_
_
0 0
1 0
_
_
_ , 0
_
_
_
0 0
0 0
_
_
_ , (6)
and idempotent, i. e. those which square to themselves,
4
_
_
_
0 0
1 1
_
_
_ , 5
_
_
_
1 0
1 0
_
_
_ , 6
_
_
_
0 1
0 1
_
_
_ , 7
_
_
_
1 1
0 0
_
_
_ , (7)
14
_
_
_
0 0
0 1
_
_
_ , 15
_
_
_
1 0
0 0
_
_
_ . (8)
The structure of this full matrix ring can be well understood from the
accompanying colour gure featuring its most important subrings, namely
those isomorphic to
GF(4) (yellow),
GF(2)[x]/x
2
(red),
GF(2) GF(2) (pink) and to
the non-commutative ring of 8/6 type (green).
Irrespectively of colour, the dashed/dotted lines join elements represented
by upper/lower triangular matrices, while the solid lines link elements rep-
resented by diagonal parity preserving matrices.
It is worth mentioning a very interesting symmetry of the picture. Namely,
the dpp ring of 8/6 type (solid green) incorporates both the upper and
lower triangular matrix rings isomorphic to GF(2)GF(2), while, in turn,
the dpp GF(2) GF(2) ring (solid pink) is the intersection of the upper
and lower triangular matrix rings of 8/6 type.
It is also to be noted that GF(4) has only one representative, the dpp
set, whereas each of the remaining types have three distinct (namely up-
per and lower triangular, and dpp) representatives. The shaded circles
denote non-trivial idempotents.
0
5 7
15 14
4 6
10 3 8
13 12
11 2 9
1
M (GF(2))
2
zd
u
Figure 1: The subrings of M
2
(GF(2)).
P
1
(M
2
(GF(2)))
Checking rst for admissibility (Eq. (1)) and then grouping the admissible
pairs left-proportional by a unit into equivalence classes (of cardinality six
each), we nd that P
1
(M
2
(GF(2))) possesses altogether 35 points, with
the following representatives of each equivalence class:
(1, 1), (1, 2), (1, 9), (1, 11), (1, 12), (1, 13),
(1, 0), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 10), (1, 14), (1, 15),
(0, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (10, 1), (14, 1), (15, 1),
(3, 4), (3, 10), (3, 14), (5, 4), (5, 10), (5, 14), (6, 4), (6, 10), (6, 14). (9)
From Eqs. (4)(8) one can easily recognize that the representatives in the
rst row of the last equation have both entries units (1 being, obviously,
unity/multiplicative identity), those of the second and third row have one
entry unit(y) and the other a zero-divisor, whilst all pairs in the last row
feature zero-divisors in both the entries. At this point we are ready to
shown which portion of P
1
(M
2
(GF(2))) is the proper algebraic geomet-
rical setting of two-qubits.
Specic Subconguration of P
1
(M
2
(GF(2)))
To this end, we consider two distant points of the line. Taking into account
the above-mentioned three-distant-transitivity of GL(2, R), we can take
these, without any loss of generality, to be the points U := (1, 0) and
V := (0, 1). Next we pick up all those points of the line which are
either simultaneously distant or
simultaneously neighbor
to U and V . Employing the left part of Eq. (2), we nd the following six
points
C
1
= (1, 1), C
2
= (1, 2), C
3
= (1, 9),
C
4
= (1, 11), C
5
= (1, 12), C
6
= (1, 13), (10)
to belong to the rst family, whereas the right part of Eq. (2) tells us that
the second family comprises the following nine points
C
7
= (3, 4), C
8
= (3, 10), C
9
= (3, 14),
C
10
= (5, 4), C
11
= (5, 10), C
12
= (5, 14),
C
13
= (6, 4), C
14
= (6, 10), C
15
= (6, 14). (11)
Making again use of Eq. (2), one nds that the points of our special subset
of P
1
(M
2
(GF(2))) are related with each other as shown in Table 2; from
this table it can readily be discerned that
to every point of the conguration there are six neighbor and eight
distant points, and that
the maximum number of pairwise neighbor points is three.
Table 1: The distant and neighbor (+ and , respectively) relation between the points of the conguration.
The points are arranged in such a way that the last nine of them (i. e., C
7
to C
15
) form the projective line over
GF(2) GF(2).
C
1
C
2
C
3
C
4
C
5
C
6
C
7
C
8
C
9
C
10
C
11
C
12
C
13
C
14
C
15
C
1
+ + + + + + + +
C
2
+ + + + + + + +
C
3
+ + + + + + + +
C
4
+ + + + + + + +
C
5
+ + + + + + + +
C
6
+ + + + + + + +
C
7
+ + + + + + + +
C
8
+ + + + + + + +
C
9
+ + + + + + + +
C
10
+ + + + + + + +
C
11
+ + + + + + + +
C
12
+ + + + + + + +
C
13
+ + + + + + + +
C
14
+ + + + + + + +
C
15
+ + + + + + + +
The nal step is to identify these 15 points with the 15 generalized Pauli
matrices/operators of two-qubits in the following way
C
1
=
z
x
, C
2
=
y
y
, C
3
= 1
2
x
,
C
4
=
y
z
, C
5
=
y
1
2
, C
6
=
x
x
,
C
7
=
x
z
, C
8
=
y
x
, C
9
=
z
y
,
C
10
=
x
1
2
, C
11
=
x
y
, C
12
= 1
2
y
,
C
13
= 1
2
z
, C
14
=
z
z
, C
15
=
z
1
2
, (12)
where 1
2
is the 2 2 unit matrix,
x
,
y
and
z
are the classical Pauli
matrices and the symbol stands for the tensorial product of matrices,
in order to readily verify that Table 2 gives the correct commuta-
tion relations between these operators with the symbols +
and now having the meaning of non-commuting and
commuting, respectively.
3. Geometry of Two-Qubits
9+6 and 10+5 Factorizations of the Algebra of Pauli Operators
C
15
C
5
C
10
C
12
C
13
C
3
C
7
C
4
C
12
C
14
C
3
C
14
C
2
C
6
C
8
C
7
C
9
C
11
C
1
C
4
C
2
C
6
C
8
C
9
C
11
C
1
C
15
C
5
C
10
C
13
Figure 2:
The two basic factorizations of the algebra of the 15 operators of a two-
qubit system. In both the cases, two operators are joined by a line-segment
only if they are commute and the color is used to illustrate how the two
factorizations relate to each other.
The Two Factorizations in Terms of Sublines of P
1
(M
2
(GF(2)))
The 9+6 factorization (left) corresponds geometrically to the split-up of
our sub-conguration of P
1
(M
2
(GF(2))) into
the projective line over GF(2) GF(2) (bottom) and
a couple of projective lines over GF(4) sharing two points (top).
The 10+5 one (right) corresponds to the partition of the sub-conguration
into
the projective line over GF(4) (top) and
a set of ve lines over GF(2)[x]/x
2
intersecting pairwise in the line
over GF(2) (bottom).
Generalized Quadrangle of Order Two, W(2)
The second interpretation involves a generalized quadrangle, a rank two
point-line incidence geometry where two points share at most one line and
where for any point X and a line L, X / L, there exists exactly one line
through X which intersect L. The generalized quadrangle associated with
our observables is of order two, i. e., the one where every line contains three
points and every point is on three lines. Such a quadrangle has, indeed,
15 points (and, because of its self-duality, the same number of lines), each
of which is joined by a line with other six as easily discernible from the
following gure:
Figure 3:
The Two Factorizations in Terms of Geometric Hyperplanes of W(2)
The 9+6 factorization of operators (left) now corresponds geometrically to
the split-up of the quadrangle of into
its grid, i.e., a slim generalized quadrangle of order (2, 1) (bottom) and
its dual (top).
The 10+5 one (right) corresponds to the partition of the quadrangle into
one of its ovoids, i. e., a set of (ve) points that has exactly one point
in common with every line (top) and
the set of ten points that form the famous Petersen graph (bottom)
as illustrated in Figure 4:
Figure 4:
Figure 5:
If, dually, one removes from the quadrangle a spread, i. e., a set of (ve) pairwise disjoint lines
that partition the point set (Fig. 5), one gets the dual of the Petersen graph; ve lines of a spread
represent nothing but the ve maximum subsets of three mutually commuting operators each, whose
associated bases are mutually unbiased.
Correspondence Between the Two Pictures
A geometric hyperplane H of a nite geometry is a set of points such that
every line of the geometry either contains exactly one point of H, or is
completely contained in H. It is easy to verify that for the generalized
quadrangle of order two H is of one of the following three kinds:
H
ov
, an ovoid (there are six such hyperplanes);
H
cl
(X), a set of points collinear with a given point X, the point itself
inclusive (there are 15 such hyperplanes); and
H
gr
, a grid as dened above (there are 10 such hyperplanes).
On the other hand, there are, respectively, three kinds of the projective lines
over the rings of order four and characteristic two living in the projective
line P
1
(M
2
(GF(2))):
P
1
(GF(4));
P
1
(GF(2)[x]/x
2
); and
P
1
(GF(2) GF(2)).
One thus reveals a perfect parity between the three kinds of the geometric
hyperplanes of the generalized quadrangle of order two and the three kinds
of the projective lines over the rings of four elements and characteristic two
embedded in our sub-conguration of P
1
(M
2
(GF(2))), giving rise to the
three kinds of the distinguished subsets of the Pauli operators of two-qubits,
as summarized in Table 2.
Table 2:
GQ H
ov
H
cl
(X) \ {X} H
gr
PL P
1
(GF(4)) P
1
(GF(2)[x]/x
2
) P
1
(GF(2) GF(2))
TQ set of ve mutually set of six operators nine operators of a
non-commuting operators commuting with a given one Mermins square
Generalizations for N-qubits
It is surmised (quant-ph/0612179) that the algebra of the Pauli operators
on the Hilbert space of N-qubits is embodied in the geometry of the sym-
plectic polar space of rank N and order two, W
2N1
(2):
the operators (discarding the identity) answer to the points of W
2N1
(2),
their partitionings into maximally commuting subsets correspond to
spreads of the space,
a maximally commuting subset has its representative in a maximal
totally isotropic subspace of W
2N1
(2) and, nally,
commuting translates into collinear (or perpendicular).
4. Conclusion
We have demonstrated that the basic properties of a system of two in-
teracting spin-1/2 particles are uniquely embodied in the (sub)geometry
of a particular projective line, found to be equivalent to the generalized
quadrangle of order two.
As such systems are the simplest ones exhibiting phenomena like quan-
tum entanglement and quantum non-locality and play, therefore, a crucial
role in numerous applications like quantum cryptography, quantum coding,
quantum cloning/teleportation and/or quantum computing to mention the
most salient ones, our discovery thus
not only oers a principally new geometrically-underlined insight into
their intrinsic nature,
but also gives their applications a wholly new perspective
and opens up rather unexpected vistas for an algebraic geometrical
modelling of their higher-dimensional counterparts.
References
[1] Saniga, M., Planat, M., and Pracna, Projective Ring Line Encompass-
ing Two-Qubits, Theoretical and Mathematical Physics, submitted,
quant-ph/0611063.
[2] Saniga, M., Planat, M., Kibler, M. R., and Pracna, P., A classication
of the projective lines over small rings, Chaos, Solitons & Fractals,
accepted, math.AG/0605301.
[3] Saniga, M., and Planat, M., On the ne structure of the projective
line over GF(2) GF(2) GF(2), Chaos, Solitons & Fractals, in
press, math.AG/0604307.
[4] Saniga, M., and Planat, M., The projective line over the nite quo-
tient ring GF(2)[x]/x
3
x and quantum entanglement. Theoretical
background, Theoretical and Mathematical Physics, accepted, quant-
ph/0603051.
[5] Saniga, M., Planat, M., and Minarovjech, M.,
The projective line over the nite quotient ring
GF(2)[x]/x
3
x and quantum entanglement. The Mermin
magic square/pentagram, Theoretical and Mathematical Physics,
accepted, quant-ph/0603206.
[6] Planat, M., Saniga, M., and Kibler, M. R., Quantum entangle-
ment and nite ring geometry, SIGMA 2, Paper 066 (2006), quant-
ph/0605239.
[7] Saniga, M., Planat, M., and Pracna, P., A classication of
the projective lines over small rings II. Non-commutative case,
math.AG/0606500.
[8] Polster, B., A Geometrical Picture Book (Springer, New York, 1998).
[9] Polster, B., Pretty pictures of geometries, Bull. Belg. Math. Soc. 5,
417425 (1998).
[10] Polster, B., Schroth, A. E., and Van Maldeghem, H., Generalized
atland, Math. Intelligencer 23, 3347 (2001).
[11] Saniga, M., and Planat, M., Multiple qubits as symplectic polar spaces
of order two, quant-ph/0612179.
S-ar putea să vă placă și
- Tables of Racah Coefficients: Mathematical Tables SeriesDe la EverandTables of Racah Coefficients: Mathematical Tables SeriesÎncă nu există evaluări
- V.A. SmirnovDocument10 paginiV.A. SmirnovjohnnybadvibeÎncă nu există evaluări
- Pedagogical Design Focusing On Learning Difficulties - Area of CirclesDocument12 paginiPedagogical Design Focusing On Learning Difficulties - Area of CirclesNur AlimÎncă nu există evaluări
- On some equations concerning some topics of Field Theory and Gravity and String Theory. Mathematical connections and applications of κ formula regarding the Zeros of Riemann Zeta Function and some Ramanujan formulas. IVDocument145 paginiOn some equations concerning some topics of Field Theory and Gravity and String Theory. Mathematical connections and applications of κ formula regarding the Zeros of Riemann Zeta Function and some Ramanujan formulas. IVAntonio NardelliÎncă nu există evaluări
- 4041-Article Text PDF-7799-1-10-20130718Document13 pagini4041-Article Text PDF-7799-1-10-20130718Miloš BasarićÎncă nu există evaluări
- FP3 P6 January 2006 Mark SchemeDocument5 paginiFP3 P6 January 2006 Mark SchemeFitri Azmeer NordinÎncă nu există evaluări
- Ramanujan Cubic PolynomialsDocument8 paginiRamanujan Cubic PolynomialsvodkaÎncă nu există evaluări
- Diophantine Conditions and Real or Complex Brjuno Functions: 1 Hamiltonian Chaos and The Standard MapDocument19 paginiDiophantine Conditions and Real or Complex Brjuno Functions: 1 Hamiltonian Chaos and The Standard MapStefano MarmiÎncă nu există evaluări
- Chapter 9 SolutionsDocument99 paginiChapter 9 Solutionsapi-2098686360% (1)
- HttpsDocument38 paginiHttpssmileforeverÎncă nu există evaluări
- Chap13 Et Student SolutionsDocument82 paginiChap13 Et Student SolutionsCody MichelÎncă nu există evaluări
- Lab Manual of LcsDocument34 paginiLab Manual of LcsEngr Muhammad Talha IslamÎncă nu există evaluări
- On the possible mathematical connections between some “solutions of the Born–Infeld constraints corresponding to the cubic Curves”, some Ramanujan formulas, the κ formula regarding the Riemann Zeta Function and some expressions concerning the Supersymmetry BreakingDocument110 paginiOn the possible mathematical connections between some “solutions of the Born–Infeld constraints corresponding to the cubic Curves”, some Ramanujan formulas, the κ formula regarding the Riemann Zeta Function and some expressions concerning the Supersymmetry BreakingMichele NardelliÎncă nu există evaluări
- EX2 PrepDocument11 paginiEX2 PrepmiguelitolinÎncă nu există evaluări
- C4 Bronze 4Document18 paginiC4 Bronze 4Betty MakharinskyÎncă nu există evaluări
- Global Iterative Solution Dielectric Spectroscopv Equations: Sylvie Remi VaillancourtDocument6 paginiGlobal Iterative Solution Dielectric Spectroscopv Equations: Sylvie Remi VaillancourtVia GshÎncă nu există evaluări
- Aieee Paper 2008Document30 paginiAieee Paper 2008Ravi LorventÎncă nu există evaluări
- Workshop 10 SolutionsDocument4 paginiWorkshop 10 SolutionsSteve DruryÎncă nu există evaluări
- WAJA 2009: Additional Mathematics Form FourDocument16 paginiWAJA 2009: Additional Mathematics Form FourTohTzeLeaÎncă nu există evaluări
- The Invariant Relations of 3D To 2D Projection of Point SetsDocument10 paginiThe Invariant Relations of 3D To 2D Projection of Point SetsEASACOLLEGEÎncă nu există evaluări
- A Generalization O.F The Connection Between The FibonacciDocument11 paginiA Generalization O.F The Connection Between The FibonacciRaskoJovanovicÎncă nu există evaluări
- On The Signless Laplacian Spectral Radius of Some GraphsDocument3 paginiOn The Signless Laplacian Spectral Radius of Some Graphsivy_publisherÎncă nu există evaluări
- Add Math SPM 2014 Modul Melaka GemilangDocument65 paginiAdd Math SPM 2014 Modul Melaka GemilangCikgu Faizal71% (7)
- Geometric Computing in Computer Graphics Using Conformal Geometric AlgebraDocument10 paginiGeometric Computing in Computer Graphics Using Conformal Geometric AlgebraneilwuÎncă nu există evaluări
- Quiz 1 (Chapter 14) - SolutionsDocument12 paginiQuiz 1 (Chapter 14) - Solutionsxperia30Încă nu există evaluări
- Research Progress: 1 Routine StuffDocument5 paginiResearch Progress: 1 Routine StuffchichieinsteinÎncă nu există evaluări
- Analyzing various equations concerning some topics of Field Theory, String Theory and Gravity. Mathematical connections and applications of κ formula regarding the Zeros of Riemann Zeta Function and Ramanujan Mathematics. IIIDocument129 paginiAnalyzing various equations concerning some topics of Field Theory, String Theory and Gravity. Mathematical connections and applications of κ formula regarding the Zeros of Riemann Zeta Function and Ramanujan Mathematics. IIIAntonio NardelliÎncă nu există evaluări
- International Journal of Mathematics and Statistics Invention (IJMSI)Document5 paginiInternational Journal of Mathematics and Statistics Invention (IJMSI)inventionjournalsÎncă nu există evaluări
- Solutions To Peskin & Schroeder: 1 Weak-Interaction Contributions To The Muon G 2Document10 paginiSolutions To Peskin & Schroeder: 1 Weak-Interaction Contributions To The Muon G 2Andres PalchucanÎncă nu există evaluări
- Paper 2 Set 1Document8 paginiPaper 2 Set 1smkpthoeÎncă nu există evaluări
- Iit 2008Document34 paginiIit 2008skbothÎncă nu există evaluări
- SQP Maths Class Xii Set - II 2015-2016Document22 paginiSQP Maths Class Xii Set - II 2015-2016kumarpvsÎncă nu există evaluări
- Math Sample Paper-1 (With Solutions)Document21 paginiMath Sample Paper-1 (With Solutions)Veeresh SavadiÎncă nu există evaluări
- On The Spectrum of Relativistic Schroedinger Equation in Finite DifferencesDocument16 paginiOn The Spectrum of Relativistic Schroedinger Equation in Finite DifferencesBayer MitrovicÎncă nu există evaluări
- Algebraic Methods To Compute Mathieu Functions - FrenkelDocument11 paginiAlgebraic Methods To Compute Mathieu Functions - FrenkelJ Jesús Villanueva GarcíaÎncă nu există evaluări
- Section 16.7 Triple Integrals in Cylindrical Coordinates: Z (R, Theta)Document5 paginiSection 16.7 Triple Integrals in Cylindrical Coordinates: Z (R, Theta)Alex TanÎncă nu există evaluări
- Error Correcting Codes From General Linear Groups: Mahir Bilen CanDocument12 paginiError Correcting Codes From General Linear Groups: Mahir Bilen CanMd. Adnan NabibÎncă nu există evaluări
- Penrose DiagramsDocument9 paginiPenrose Diagramsbastian_wolfÎncă nu există evaluări
- AIEEE2011 PaperDocument11 paginiAIEEE2011 PaperRavi LorventÎncă nu există evaluări
- 2012 Tut 4 On APGP (Soln For Sect C and D)Document6 pagini2012 Tut 4 On APGP (Soln For Sect C and D)SamuelÎncă nu există evaluări
- Third Quarter Examination-Math Grade 10Document5 paginiThird Quarter Examination-Math Grade 10Rhumer LanojanÎncă nu există evaluări
- 11 Pre-CalculusDocument56 pagini11 Pre-CalculusJohn Laverne Capalis BocadoÎncă nu există evaluări
- Trial SPM 2014 Melaka P1 & P2 PDFDocument65 paginiTrial SPM 2014 Melaka P1 & P2 PDFrusleenaosman790% (1)
- 9 3 PDFDocument112 pagini9 3 PDFksr131Încă nu există evaluări
- Exam1 SolsDocument18 paginiExam1 SolsLeandro RibeiroÎncă nu există evaluări
- MAM2085F 2013 Exam SolutionsDocument8 paginiMAM2085F 2013 Exam Solutionsmoro1992Încă nu există evaluări
- 2013 SMCHMath T1 TrialDocument7 pagini2013 SMCHMath T1 TrialchimbiÎncă nu există evaluări
- Progress in Electromagnetics Research C, Vol. 26, 167-179, 2012Document13 paginiProgress in Electromagnetics Research C, Vol. 26, 167-179, 2012Nilkanth YengdeÎncă nu există evaluări
- 2007 HCI Prelims Paper 1 QuestionsDocument5 pagini2007 HCI Prelims Paper 1 QuestionsUmehara EriÎncă nu există evaluări
- Block Diagrams Control SystemsDocument25 paginiBlock Diagrams Control SystemsSingappuliÎncă nu există evaluări
- Lecture 5Document5 paginiLecture 5vaibhav shivhareÎncă nu există evaluări
- NoncgearDocument6 paginiNoncgearAndreea UdreaÎncă nu există evaluări
- Me352 E1 Fa2009 SolDocument21 paginiMe352 E1 Fa2009 SolSteve KrodaÎncă nu există evaluări
- Mathematics Online WWW - Mathematicsonline.co - in Three Dimensional Coordinate Assignment 3Document5 paginiMathematics Online WWW - Mathematicsonline.co - in Three Dimensional Coordinate Assignment 3Karm VeerÎncă nu există evaluări
- 1 s2.0 S0377042796001112 MainDocument17 pagini1 s2.0 S0377042796001112 MainMoti LevyÎncă nu există evaluări
- Article 31Document16 paginiArticle 31TamathÎncă nu există evaluări
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2Document15 paginiSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2jimmytanlimlongÎncă nu există evaluări
- Mathematical Tables: Tables of in G [z] for Complex ArgumentDe la EverandMathematical Tables: Tables of in G [z] for Complex ArgumentÎncă nu există evaluări
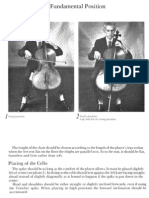
- Cello Ad BackDocument1 paginăCello Ad Backgalaxy5111Încă nu există evaluări
- The Physics of SoundDocument44 paginiThe Physics of SoundDiego PinheiroÎncă nu există evaluări
- Tasty MushroomDocument1 paginăTasty Mushroomgalaxy5111Încă nu există evaluări
- Cello TechniqueDocument5 paginiCello Techniquegalaxy5111100% (8)
- Cpemh 8 110Document10 paginiCpemh 8 110galaxy5111Încă nu există evaluări
- PB Hallebeek - Guidelines For The Conservation of Leather and Parchment Book-BindingsDocument73 paginiPB Hallebeek - Guidelines For The Conservation of Leather and Parchment Book-Bindingsgalaxy5111100% (3)
- 7 PointsDocument4 pagini7 Pointsgalaxy5111100% (1)
- Cello Extended TechniquesDocument30 paginiCello Extended TechniquesFábio Videira100% (6)
- IngwersenDocument11 paginiIngwersengalaxy5111Încă nu există evaluări
- Rly Eh SutraDocument25 paginiRly Eh Sutragalaxy5111Încă nu există evaluări
- 252 McleodDocument12 pagini252 Mcleodgalaxy5111Încă nu există evaluări
- Latin For Mountain MenDocument58 paginiLatin For Mountain Mengalaxy5111Încă nu există evaluări
- How To Sew A Book BlockDocument14 paginiHow To Sew A Book Blockgalaxy5111100% (1)
- Bookcraft BookRepairGuideDocument35 paginiBookcraft BookRepairGuidegalaxy5111Încă nu există evaluări
- 10916Document157 pagini10916galaxy5111Încă nu există evaluări
- Derek Jansen - The Science of The Stars in Danzig - From Rheticus To Hevelius (331pp)Document331 paginiDerek Jansen - The Science of The Stars in Danzig - From Rheticus To Hevelius (331pp)galaxy5111Încă nu există evaluări
- Language of CreationDocument654 paginiLanguage of Creationgalaxy511198% (45)
- Failure and Sensitivity Analysis of A Reconfigurable Vibrating Screen Using Finite Element AnalysisDocument12 paginiFailure and Sensitivity Analysis of A Reconfigurable Vibrating Screen Using Finite Element Analysisالمشري بدوÎncă nu există evaluări
- Calculation of The Equivalent Resistance and Impedance of The Cylindrical Network Based On Recursion-Transform MethodDocument12 paginiCalculation of The Equivalent Resistance and Impedance of The Cylindrical Network Based On Recursion-Transform Methodmark_990566444Încă nu există evaluări
- WK 4 Intuitive Thinking and Strategic AnalysisDocument10 paginiWK 4 Intuitive Thinking and Strategic AnalysisMARY LORD GERALDINE VELASCOÎncă nu există evaluări
- Lab11 - Sequential System Design Using ASM ChartsDocument7 paginiLab11 - Sequential System Design Using ASM Chartswert1a2Încă nu există evaluări
- Borang Rekod Ujian Diagnostik: Mathematics Diagnostic Test Record FormDocument6 paginiBorang Rekod Ujian Diagnostik: Mathematics Diagnostic Test Record FormNarmatha MoganÎncă nu există evaluări
- Week 4 DLL-WK-13-LC-2021Document15 paginiWeek 4 DLL-WK-13-LC-2021Jerson YhuwelÎncă nu există evaluări
- Lec06 - Ordinary Differential Equations (BVP) - Shooting MethodsDocument39 paginiLec06 - Ordinary Differential Equations (BVP) - Shooting MethodsALYAMITHA NADIYAH SYAFITRI BAUDÎncă nu există evaluări
- PHYsicsDocument10 paginiPHYsicsonly1fxisguruÎncă nu există evaluări
- Final Draft Final Research ProposalDocument28 paginiFinal Draft Final Research Proposalapi-432035312Încă nu există evaluări
- Chapter 2 Practice AnswersDocument4 paginiChapter 2 Practice AnswersZeyad Moustafa100% (1)
- 2nd Quaarter ExamDocument2 pagini2nd Quaarter ExamJoana Marie DeontoyÎncă nu există evaluări
- Laterally Unrestrained BeamsDocument12 paginiLaterally Unrestrained BeamsVikram0% (1)
- Applied Fluid Mechanics - 05 Bouyancy and StabilityDocument29 paginiApplied Fluid Mechanics - 05 Bouyancy and Stabilitysourz1875% (4)
- Lec1.2 IITM Week 1 Stats2Document9 paginiLec1.2 IITM Week 1 Stats2samudraneel05Încă nu există evaluări
- Bs Math Thesis TopicDocument8 paginiBs Math Thesis Topicafknjdsta100% (2)
- Area of A Parallelogram NotesDocument8 paginiArea of A Parallelogram NotesvenkatÎncă nu există evaluări
- Faulhaber's Formula The Sum of The R-TH Powers of The First N Positive Integers Is Given byDocument1 paginăFaulhaber's Formula The Sum of The R-TH Powers of The First N Positive Integers Is Given byVice SonÎncă nu există evaluări
- CFDADVDocument183 paginiCFDADVKumar ChowdaryÎncă nu există evaluări
- Pengembangan Instrumen Tes Untuk Mengukur Kemampuan Berpikir Komputasi SiswaDocument10 paginiPengembangan Instrumen Tes Untuk Mengukur Kemampuan Berpikir Komputasi Siswaaliidrus2602Încă nu există evaluări
- Topology An Introduction To The Point-Set and Algebraic - Kahn, Donald W., 1935 - 1995 - New York Dover - 9780486686097 - Anna's ArchiveDocument244 paginiTopology An Introduction To The Point-Set and Algebraic - Kahn, Donald W., 1935 - 1995 - New York Dover - 9780486686097 - Anna's ArchiveSin NombreÎncă nu există evaluări
- Process SynchronizationDocument23 paginiProcess Synchronizationwowafer745Încă nu există evaluări
- Engineering Mathematics IIDocument102 paginiEngineering Mathematics IIIsaac P PlanÎncă nu există evaluări
- False Data Injection Attacks On LFC Systems An AI-Based Detection and Countermeasure StrategyDocument9 paginiFalse Data Injection Attacks On LFC Systems An AI-Based Detection and Countermeasure StrategyAmar IndraÎncă nu există evaluări
- EC2314Document3 paginiEC2314Rakesh Kumar DÎncă nu există evaluări
- Statistical ThermodynamicsDocument8 paginiStatistical ThermodynamicsDora Rabêlo100% (1)
- Y17 Statics - Force Systems - Problems PDFDocument30 paginiY17 Statics - Force Systems - Problems PDFJerico CruelÎncă nu există evaluări
- Notation For Differentiation - WikipediaDocument11 paginiNotation For Differentiation - WikipediaTibor VéghÎncă nu există evaluări
- Aminpro Addin Guide 1.2-1Document16 paginiAminpro Addin Guide 1.2-1John Calero OrtegaÎncă nu există evaluări
- Calculation Algorithm For Single Phase Bridge Rectifier With Capacitor FilterDocument7 paginiCalculation Algorithm For Single Phase Bridge Rectifier With Capacitor FilterAhmedÎncă nu există evaluări
- Centroids, Centre of Mass & Centres of GravityDocument42 paginiCentroids, Centre of Mass & Centres of GravityGray RagudosÎncă nu există evaluări


























































![Mathematical Tables: Tables of in G [z] for Complex Argument](https://imgv2-2-f.scribdassets.com/img/word_document/282615796/149x198/febb728e8d/1714993295?v=1)