Mtodos Numricos

Dr. Roberto Aravire Flores

Abril de 2014
1 Resolucin de Ecuaciones No Lineales
Un problema fundamental de las matemticas aplicadas es determinar valores
c tales que ,(c) = 0. Estos valores se denominan races de la ecuacin
,(r) = 0
En general no es posible resolver una ecuacin como esta y por lo tanto en-
contrar los valores exactos no es alcanzable en todos los casos, por esto se han
desarrollado mtodos que permiten determinar aproximaciones numricas su-
cientemente cercanas a las races buscadas. El siguiente ejemplo ilustra el
tipo de problemas que queremos estudiar:
Problema: En los estudios sobre recoleccin de energa solar al enfocar
un campo de espejos planos en un colector solar central, un investigador
obtuvo la siguiente ecuacin para el factor de concentracin geomtrica C:
C =
:(/, cos )
2
1
0.51
2
(1 + sin 0.5 cos )
.
donde es el ngulo de anillo del campo, 1 es la cobertura fraccionaria del
campo con los espejos, 1 es el dimetro del colector y / es la altura del
mismo. Encuentre , si / = 300, C = 1200, 1 = 0.8 y 1 = 14.
Para resolver este tipo de problemas consideraremos 3 mtodos que ilus-
tran el tipo de argumentos y herramientas usadas en clculo numrico.
1
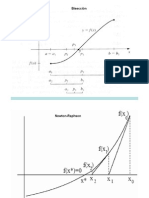
1.1 Mtodo de la Biseccin
Est basado en el Teorema del Valor Intermedio que dice: Si ,(r) una
funcin real tal que ,(c) y ,(/) tienen signos distintos y adems es continua
en un intervalo que incluye a [c. /], entonces existe c [c. /] tal que ,(c) = 0.
De este modo debemos determinar dos puntos c y / donde la funcin
, cambie de signo, esto es posible mediante el uso de la funcin j|ot de
Maple, de modo que supongamos que ya tenemos estos valores. El mtodo
consiste en considerar el punto medio c entre ambos extremos y determinar
donde se produce el cambio de signo, en [c. c] o en [c. /], segn corresponda
se descarta uno de los dos intervalos y se contina con el restante, al que se
aplica el mismo procedimiento. De este modo en cada iteracin del proceso
la amplitud del intervalo se reduce a la mitad y la raiz buscada quedar
encerrada en el intervalo restante. El intervalo inicial tiene amplitud / c,
de este modo, despus de : iteraciones, obtendremos un intervalo de amplitud
(/ c),2
n1
.
Este mtodo permite obtener una sucesin r
i
donde cada r
i
es el punto
medio obtenido en cada iteracin. Dado que la amplitud del intervalo tiende
a 0, tenemos que la sucesin es convergente y su lmite es una de las races
buscadas.
En el documento adjunto se incluye un programa en Maple que permite
aplicar este mtodo.
Ejercicios:
1. Encuentre la menor raiz positiva de la funcin trascendente
,(r) = 3r + sin r c
x
Cuntas races existen?
2. La funcin ,(r) = r cos(r,(r 2)) tiene muchos ceros, especialmente
cerca de r = 2, donde est indenida. Trace la grca de la funcin.
Determine las cuatro primeras races positivas aplicando el mtodo de
la biseccin, obtengas estas races con hasta 6 dgitos signicativos
exactos.
2
3. Encuentre, mediante el mtodo de la biseccin, las coordenadas de los
puntos dende se cortan las grcas de = r
2
2 e = c
x
con hasta
6 cifras decimales exactas. Cuntas iteraciones se requieren?
1.2 Metodo de Newton - Raphson
Este mtodo es uno de los ms utilizados y est basado en aproximaciones
lineales de ,. Para deducir el mtodo recurriremos a la serie de Taylor de la
funcin, la que supondremos tiene todas sus derivadas en una vecindad que
incluya a la raiz buscada. Sea r
0
una paroximacin inicial, desarrollemos la
serie de Taylor de , alrededor de r
0
, entonces
,(r) = ,(r
0
) +,
0
(r
0
)(r r
0
) + +
1
:!
,
(n)
(r
0
)(r r
0
)
n
+
Considerando r cercano a r
0
tenemos que las potencias de rr
0
deben ser
muy pequeas lo que permite truncar la serie a partir de la segunda derivada,
de este modo obtenemos:
,(r) t ,(r
0
) +,
0
(r
0
)(r r
0
)
con un error dado por la segunda derivada de ,. Ms an como la raiz c es
cercana a r
0
podemos especializar r = c, obteniendo, dado que ,(c) = 0
0 t ,(r
0
) +,
0
(r
0
)(c r
0
)
de donde concluimos que:
c t r
0

,(r
0
)
,
0
(r
0
)
Esta aproximacin nos permite construir una nueva y mejor aproximacin
r
1
= r
0

,(r
0
)
,
0
(r
0
)
e iterando el procedimiento
r
n+1
= r
n

,(r
n
)
,
0
(r
n
)
para : _ 1.
3
Nota: Cabe destacar que este mtodo no converge cuando la primera
derivada es 0 o muy cercana a 0, en tal caso, se puede recurrir a un trmino
ms en la serie de Taylor para obtener una aproximacin mejor, en este caso
obtendremos una aproximacin de carcter cuadrtica en la que an podemos
despejar c.
En el documento adjunto se incluye un programa en Maple que permite
aplicar este mtodo.
Ejercicios:
1. Un mtodo similar al de la Biseccin es el Mtodo de Interpolacin Lin-
eal, consiste en determinar como aproximacin el punto de interseccin
de la recta que une (c. ,(c)) y (/. ,(/)) , con el eje A.
(a) Aplique este mtodo para determinar la raiz de ,(r) = r
3
+r
2

3r 3 = 0 con valores iniciales c = 1, / = 2.

(b) Redacte un programa en Maple que desarrolle este mtodo.
2. Mtodo de Gree para separar races de polinomios. A veces las races
de un polinomio estn muy cercanas, por lo que los mtodos usuales
no convergen, este mtodo permite construir un nuevo polinomio cuyas
races son los cuadrados de las races originales, por lo tanto ests
races quedarn ms separadas. sea 1(r) un polinomio, considere el
producto 1(r)1(r), este nuevo polinomio es tal que la variable r se
encuentra siempre elevado a potencias pares. reemplazando . = r
2
,
obtenemos un polinomio en . que tiene el mismo grado que el original
pero con races que son el cuadrado de las races del polinomio original.
Demuestrelo.
3. Confeccione un programa en Maple que permita aplicar el mtodo de
Bairstow.
4. Encuentre los puntos mximo/mnimo de la funcin
,(r) = [sin(r)]
6
c
20x
tan(1 r)
sobre el intervalo [0. 1].
4
5. Aplique el mtodo de Newton para calcular las races de
,(r) = c
x
+ 4r
3
5
con una precisin de hasta el quinto decimal, determine el nmero de
iteraciones necesarias para lograr esta aproximacin.
6. Use el mtodo de Newton en la ecuacin r
2
= ` para deducur el
algoritmo para obtener la raiz cuadrada de `;
r
n+1
=
1
2
_
r
n
+
`
r
n
_
.
7. Encuentre las races (reales o complejas), mediante el mtodo de New-
ton - Raphson, de las siguientes ecuaciones:
(a) 3r
3
+ 2r
2
r 6
(b) r
3
r
2
1
(c) r
3
c
2x
+ 1
8. Determine las races del polinomio
r
5
11r
4
+ 46r
3
90r
2
+ 81r 27
(a) Es posible obtener todas las races por biseccin?
(b) Qu ocurre con el mtodo de Newton (hay races mltiples).
9. Encuentre los puntos mximos o mnimos de la funcin
,(r) = [sin r]
6
c
20x
tan(1 r)
en el intervalo [0. 1]. Utilice cualquier mtodo.
10. El polinomio j(r) = r
3
+ 94r
2
389r + 294 tiene como races a 1, 3,
-98. El punto r
0
= 2 debera ser en este caso un buen punto inicial
para calcular cualquiera de las races pequeas por medio de iteraciones
de Newton. Haga los clculos y explique lo que sucede.
5
1.3 Mtodo de Newton - Raphson Generalizado
Este mtodo permite obtener las races de sistemas de : funciones no lineales
de : variables. Est basado en las series de Taylor de variables mltiples, las
que se truncan manteniendo su parte lineal, siguiendo la misma estrategia
que en la seccin anterior obtenemos un sistema lineal de : ecuaciones con
: incgnitas ( las incgnitas son las componentes de un punto interseccin
de las supercies ) (r
1
. r
1
. . . . . r
n
)
En el caso : = 2, las funciones son
1(r. ) = 0
G(r. ) = 0
y un punto de interseccin de estas curvas (c. ,) , se puede aproximar
mediante una sucesin de puntos (r
n
.
n
) obtenidos de la siguiente manera:
r
n+1
= r
n

1(r
n
.
n
) 1
y
(r
n
.
n
)
G(r
n
.
n
) G
y
(r
n
.
n
)

1
x
(r
n
.
n
) 1
y
(r
n
.
n
)
G
x
(r
n
.
n
) G
y
(r
n
.
n
)

n+1
=
n

1
x
(r
n
.
n
) 1(r
n
.
n
)
G
x
(r
n
.
n
) G(r
n
.
n
)

1
x
(r
n
.
n
) 1
y
(r
n
.
n
)
G
x
(r
n
.
n
) G
y
(r
n
.
n
)

donde el determinante

1
x
(r
n
.
n
) 1
y
(r
n
.
n
)
G
x
(r
n
.
n
) G
y
(r
n
.
n
)

es el Determinante Ja-
cobiano del Sistema.
En el documento adjunto se incluye un programa en Maple que permite
aplicar este mtodo.
Ejercicios:
6
1. Considere las siguientes funciones
1(r. ) = r
3
2
2
10
G(r. ) = r
2
3r
3
+ 3
Determine los puntos de interseccin entre estas curvas. Para ello
efectue primero una gracacin y luego, partiendo de diversas aproxi-
maciones, determine los puntos de interseccin.
2. En Anlisis Numrico con Aplicaciones de Gerald & Wheatley y en
otros textos se encuentran una variedad de mtodos. Revise estos mto-
dos, son variaciones de los que hemos presentado.
(a) Mtodo de Interpolacin Lineal
(b) Mtodo de Muller
(c) Mtodo de Newton para Polinomios
(d) Mtodo de Bairstow para factores cuadrticos
(e) Mtodos para races mltiples.
3. Para efectuar Integracin Numrica se utiliza un mtodo denominado
Cuadratura Gaussiana. Para esto es necesario determinar los ceros
de los polinomios de Legendre. Encuentre los ceros del polinomio de
Legendre de sexto orden
1
6
(r) =
1
48
(693r
6
945r
4
+ 315r
2
15)
Similarmente encuentre los ceros de los polinomios de Laguerre:
(a) 1
3
(r) = r
3
9r
2
+ 18r 6
(b) 1
4
(r) = r
4
16r
3
+ 72r
2
96r + 24
4. Determine las races de las ecuaciones simultneas
(r 4)
2
+ ( 4)
2
= 4
r
2
+
2
= 16
Use una aproximacin grca para obtener los valores iniciales.
7
5. Repita el problema anterior para
= r
2
+ 1
= 3 cos r
6. Localice la primera raz positiva de
,(r) = sin(r) + cos(1 + r
2
) 1
donde r est en radianes. Mediante grcos determine una primera
aproximacin y luego use 4 iteraciones con el mtodo de Newton-
Raphson.
7. El mtodo de divide y promedia, un antiguo mtodo para aproximar
la raiz cuadrada de cualquier nmero positivo c, se puede formular
como
r =
r +c,r
2
Demuestre que esta frmula est basada en el algoritmo de Newton-
Raphson.
8. Efecte iteraciones con el Mtodo de Newton Generalizado para el sis-
tema siguiente
1(r. ) = 1 +r
2

2
+c
x
cos
G(r. ) = 2r +c
x
sin
con valores iniciales r
0
= 1 e
0
= 4 .
8
2 Aproximacin de Funciones
Otro problema fundamental en matemticas aplicadas es cmo aproxi-
mar funciones mediante funciones elementales?, las elementales son las fun-
ciones polinmicas, trigonomtricas, funciones racionales (cuociente de poli-
nomios), exponenciales, etc. En particular, desde un punto de vista prctico
es muy importante aproximar una funcin mediante funciones elementales
que involucren el menor nmero posible de operaciones y que stas sean el-
ementales. En el caso de las calculadoras, se desea representar las funciones
trigonomtricas, logaritmicas, exponenciales y otras, a partir de multiplica-
ciones, sumas y restas, este tipo de habilidades son las que transforman a
una calculadora usual en una cientca.
2.1 Aproximaciones de Taylor
Cuando la funcin es continua y derivable todas las veces necesarias, se puede
construir su serie de Taylor alrededor de algn punto r
0
. As tenemos
,(r) = c
0
+c
1
(r r
0
) +c
2
(r r
0
)
2
+c
3
(r r
0
)
3
+ +c
n
(r r
0
)
n
+
donde c
n
=
1
:!
,
(n)
(r
0
) y esta representacin es vlida en una cierta
vecindad de r
0
de radio 1 (radio de convergencia) donde se produce
la convergencia uniforme lo que permite realizar operaciones fundamentales
trmino a trmino tales como derivacin e integracin.
De esta manera truncando la serie en algn trmino obtenemos
,(r) - c
0
+c
1
(r r
0
) +c
2
(r r
0
)
2
+c
3
(r r
0
)
3
+ +c
n
(r r
0
)
n
es decir, la funcin ,(r) aproximada por un polinomio. Por ejemplo,
sin r - r
r
3
3!
+
r
5
5!

r
7
7!
+
r
9
9!
Con esta aproximacin podemos calcular sin(n) evaluando un polinomio de
grado 9. Los problemas que surgen son: cul es el error cometido?, es
posible encontrar otro polinomio del mismo grado que d menos error?
La primera pregunta se responde por medio de la frmula
[1
T
[ _ [,
(n+1)
(r
1
) (r r
0
)
n+1
[,:!
9
donde r
1
es un punto en el intervalo en que se est trabajando.
En el Taller 2 se estudia el caso de ,(r) = sin r, con [c. /] = [:,2. :,2],
y se verica que la distribucin del error no es uniforme en el intervalo, de
hecho para esta funcin, los valores del error crecen violentamente en los
extremos del intervalo.
En el mismo Taller se revisan los grcos de cada elemento de la base
1. r. r
2
. r
3
. r
4
. . . . . r
n
. . . . del conjunto de polinomios (A).
La poca uniformidad de la distribucin de errores para esta base hace que
se estudien bases alternativas de (A) y funciones de ponderacin (pesos) que
den mayor importancia a los extremos. En la siguiente seccin veremos una
base distinta de polinomios y una funcin peso que permitir una distribucin
ms uniforme.
2.2 Polinomios de Chebyshev
Consideremos el Espacio J[1. 1] de Funciones Reales Cuadrtico-Integrables
sobre el intervalo [1. 1] con el producto
< ,. q =
_
1
1
,(r)q(r)
_
1 r
2
dr
donde n(r) =
1
_
1 r
2
es la funcin peso, da mayor mayor importancia a
los extremos del intervalo y caracteriza este producto.
(J[ 1. 1]. < . ) es Espacio Vectorial Euclidiano, es decir, < .
es producto interior de denicin positiva.
Ejercicio: Demuestre que
1. < ,. q =< q. ,
2. < ,. q +/ =< ,. q + < ,. /
3. < ,. `q = ` < ,. q para todo real `.
4. < ,. , _ 0, en particular < ,. , = 0 implica que , es cero salvo un
nmero nito de puntos.
10
Es posible, mediante el proceso de Gram-Schmidt, encontrar una base
ortogonal de este espacio, sin embargo recurriremos a la siguiente denicin
para determinar una base ortogonal.
Denicin: Para 1 _ r _ 1, sea o = arccos r, es decir o [0. :].
Denimos
1
n
(r) = cos(:o)
De la denicin se obtiene:
1
0
(r) = cos(0o) = 1
1
1
(r) = cos(o) = r
1
2
(r) = cos(2o) = 2r
2
1
1
3
(r) = cos(3o) = 4r
3
3r
1
4
(r) = cos(4o) = 8r
4
8r
2
+ 1
En general es un tedioso calcular 1
n
(r) para : _ 4, por ello se utiliza la
siguiente frmula:
1
n+1
(r) = cos((: + 1)o) = cos(:o) cos o sin(:o) sin o
1
n1
(r) = cos((: 1)o) = cos(:o) cos o + sin(:o) sin o
Sumando ambas igualdades obtenemos
1
n+1
(r) +1
n+1
(r) = 2 cos(:o) cos o = 2r1
n
(r)
es decir
1
n+1
(r) = 2r1
n
(r) 1
n1
(r)
para todo : _ 1. Esta es la Frmula de Recurrencia de los Polinomios de
Chebyshev.
Propiedades:
1. 1
n
(r) es polinomio de grado :.
2. El coeciente principal de 1
n
(r) es 2
n1
, para : _ 1.
11
3. 1
n
(r) es funcin cuya paridad corresponde a la paridad de :.
4. [1
n
(r)[ _ 1 para todo r [1. 1].
5. 1
n
(1) = 1
6. 1
n
(1) = (1)
n
Ejercicios:
1. Demuestre las propiedades anteriores.
2. Determine 1
n
(0).
Un hecho sorprendente es que estos polinomios de Chebyshev constituyen
una base orotogonal de [1. 1] y en consecuencia de (J[ 1. 1]. < .
). Dado que el grado de 1
n
(r) es :, resulta evidente que el conjunto de
polinomios de Chebyshev es una base, el hecho que sea ortogonal se obtiene
del siguiente clculo:
< 1
m
(r). 1
n
(r) =
_
1
1
1
m
(r)1
n
(r)
_
1 r
2
dr =
cambiando variable r = cos o, dr = sin odo, obtenemos
_
1
1
1
m
(r)1
n
(r)
_
1 r
2
dr =
_
0

cos(:o) cos(:o)
_
1 cos
2
o
(sin o)do
=
_

0
cos(:o) cos(:o)do
=
1
2
_

0
[cos(:+:)o + cos(::)o] do
=
1
2
_
sin(:+:)o
:+:
+
sin(::)o
::
_

0
= 0
De este modo los polinomios de Chebyshev son ortogonales.
12
Ms an, con argumentos similares se demuestra que:
< 1
n
(r). 1
n
(r) =
_
_
_
:,2 para : _ 1
: para : = 0
El Teorema de Weierstrass garantiza que los polinomios son densos en J[
1. 1] de modo que podemos representar una funcin ,(r) como serie de los
1
n
(r)
,(r) = c
0
1
0
(r) +c
1
1
1
(r) +c
2
1
2
(r) + +c
n
1
n
(r) +
para todo r [1. 1].
Es fcil vericar que
c
n
=
_

_
1

_
1
1
f(x)
p
1x
2
dr para : = 0
2

_
1
1
f(x)Tn(x)
p
1x
2
dr para : _ 1
Ejemplo: Si ,(r) = 3 +r r
3
, entonces
,(r) = 31
0
(r)
1
4
1
1
(r)
1
4
1
3
(r)
La razn para la eleccin de los polinomios de Chebyshev, es que dis-
tribuyen el error de manera uniforme, es decir, comparado con polinomios
del mismo grado y mismo coeciente principal, los polinomios de Chebyshev
tienen menor error uniforme.
Demostracin. Dado que el coeciente principal de los polinomios de
Chebyshev 1
n
(r) es 2
n1
, consideremos los polinomios t
n
(r) = 2
(n1)
1
n
(r),
es polinomios multiplos de los de Chebyshev pero con coeciente principal 1,
entonces la variacin mxima de t
n
(r) es 2
(n1)
(que es alcanzada en :+1
puntos, dado que 1
n
(r) es un coseno). Supongamos que existe un polinomio
de grado :, con coeciente principal 1 que tiene variacin menor que la de
t
n
(r) en [1. 1], es decir
max
x2[1;1]
(r) < max
x2[1;1]
t
n
(r)
13
Entonces la grca de corta a la grca de t
n
en, al menos, : puntos. Por
lo tanto el polinomio t
n
debe tener grado mayor o igual que :. Pero esto
es imposible porque t
n
es un polinomio diferencia entre dos de grado :
con el mismo coeciente principal, es decir deg( t
n
) < : Contradiccin.
En consecuencia no existe un polinomio de grado :, con coeciente prin-
cipal 1 que tiene variacin menor que la de t
n
(r) en [1. 1]. Es decir los
polinomios de Chevyshev son los de variacin minimal.
Ejercicios:
Determine la serie de Chebyshev de
1. ,(r) =
_
1 r
2
2. ,(r) = [r[
3. ,(r) = (1 r
2
)
3=2
4. Calcule 1
6
(r) a 1
10
(r).
5. Extienda las grcas de 1
1
(r), 1
2
(r), 1
3
(r) al intervalo [2. 2].
Observe que la magnitud mxima de los polinomios de Chebyshev no
es igual a la unidad fuera de [1. 1].
6. Determine la Serie de Chebyshev de las siguientes funciones
(a) ,(r) = 4r
4
+r
3
5r + 2
(b) ,(r) = [r[.
14
3 Ms Aproximacin de Funciones
En esta ocasin continuamos trabajando con el problema de aproximacin
de funciones mediante funciones elementales. Hemos visto que existe un tipo
especial de polinomios que son ortogonales respecto a un peso que pondera
el intervalo [1. 1] dando importancia a los extremos del intervalo. Este
tipo especial de polinomios, llamados Polinomios de Chebyshev, tienen la
propiedad de ser ptimos respecto a la distribucin del error. Por la ortog-
onalidad es posible expresar una funcin mediante serie de polinomios de
Chabyshev. Desarrollando estos polinomios obtenemos una representacin
de esa funcin como serie de potencias en una versin distinta a la obtenida
mediante el desarrollo de Taylor.
El inconveniente de esta representacin es que se deben evaluar integrales
numricas que utilizan la propia representacin de ,(r), aunque en puntos
muy especcos.
En esta reunin analizaremos alternativas o complementos al trabajo con
series de Chebyshev, en particular el mtodo de economizacin de series
truncadas y la aproximacin mediante funciones racionales.
3.1 Series de Potencias Economizadas
Consideremos la serie de Maclaurin para sin(r)
sin(r) = r
r
3
6
+
r
5
120

r
7
5040
+
Para usar una serie truncada para aproximar sin(r) en [1. 1] con una pre-
cisin de 0.000001, sera necesario retener trminos hasta r
7
. Supongamos
que sumamos
_
1
5040
__
1
7
64
_
a la serie truncada, entonces se tiene que desaparece el trmino con r
7
y se
realizan modicaciones a otros coecientes de la serie. Dado que [1
7
[ _ 1, la
modicacin realizada modica la serie slo en
1
5040

1
64
< 3.1 10
6
15
que es pequeo respecto a la precisin requerida.
Al realizar los clculos se obtiene un polinomio de grado 5 que se aproxima
a la funcin tan bien como el polinomio de de grado 7 de Maclaurin. Desde
este punto de vista la serie de potencias se ha economizado en el sentido que se
obtien presicin similar pero con menos trminos. Ms an es posible efectuar
otras economas que permitan disminuir ms an el nmero de trminos de
la representacin.
Los reemplazos efectuados estn basados en la siguiente lista:
1 = 1
0
r = 1
1
r
2
=
1
2
(1
0
+1
2
)
r
3
=
1
4
(31
1
+1
3
)
r
4
=
1
8
(31
0
+ 41
2
+1
4
)
r
5
=
1
16
(101
1
+ 51
3
+1
5
)
r
6
=
1
32
(101
0
+ 151
2
+ 61
4
+1
6
)
r
7
=
1
64
(351
1
+ 211
3
+ 71
5
+1
7
)
.
.
.
3.2 Aproximacin con Funciones Racionales
An con la generacin de Polinomios especiales como los de Chebyshev y
el sistema de economizar trminos, desde el punto de vista prctico an es
posible optimizar la aproximacin en trminos del nmero de clculos y la
facilidad de ellos. Una de los procedimientos ms simples es la Aproximacin
mediante Funciones Racionales, es decir, mediante cocientes de polinomios,
denominada Aproximaciones de Pad. Supongamos que
,(r) = 1
N
(r) =
c
0
+c
1
r +c
2
r
2
+c
3
r
3
+ +c
n
r
n
1 +/
1
r +/
2
r
2
+/
3
r
3
+ +/
m
r
m
16
donde ` = : + : y el trmino constante en el denominador ha sido con-
siderado 1, sin prdida de generalidad. Estas aproximaciones son ms tiles
cuando el grado del numerador es igual o mayor en 1 al del denominador.
Para determinar los coecientes c
i
, /
i
desarollamos la serie de Maclaurin
de ,(r) (hasta r
N
) de este modo se obtiene un sistema de ` ecuaciones
con ` incognitas que puede ser resuelto y as obtenemos los valores de los
coecientes de la aproximacin.
Ejemplo: Aproximemos arctan(r) mediante 1
9
. Usemos como numer-
ador un polinomio de grado 5.
arctan(r) = r
1
3
r
3
+
1
5
r
5

1
7
r
7
+
1
9
r
9
Entonces tenemos:
arctan(r) = r
1
3
r
3
+
1
5
r
5

1
7
r
7
+
1
9
r
9
=
c
0
+c
1
r +c
2
r
2
+ +c
5
r
5
1 +/
1
r +/
2
r
2
+ +/
4
r
4
Multiplicando y ordenando obtenemos:
c
0
= 0
c
1
= 1
c
2
= /
1
c
3
=
1
3
+/
2
c
4
=
1
3
/
1
+/
3
c
4
=
1
5

1
3
/
2
+/
4
1
5
/
1

1
3
/
3
= 0

1
7
+
1
5
/
2

1
3
/
4
= 0

1
7
/
1
+
1
5
/
3
= 0
1
9

1
7
/
2
+
1
5
/
4
= 0
17
Se resuelve primero el sistema para las / y luego se sustituye para determinar
las c . Obtenemos /
1
= /
3
= 0, /
2
=
10
9
, /
4
=
5
21
. c
0
= c
2
= 0, c
1
= 1,
c
3
=
7
9
, c
5
=
64
945
.
De este modo una funcin racional que aproxima a arctan(r) es:
arctan(r) -
r +
7
9
r
3
+
64
945
r
5
1 +
10
9
r
2
+
5
21
r
4
Esta aproximacin tiene un error (1/275) en el extremo r = 1.
Ejercicios
1. La aproximacin de c
x
, mediante la serie de Taylor, es
c
x
= 1 +r +
r
2
2
+
r
3
6
+
r
4
24
+
r
5
120
+
r
6
720
+
Supongamos que la serie es truncada a partir de r
7
y que se resta
_
1
720
__
1
6
32
_
de la serie truncada, entonces este proceso cancela el trmino en r
6
y
al mismo tiempo realiza ajustes en otros coecientes de la serie. De-
termine los nuevos coecientes del polinomio. Este polinomio es mejor
aproximacin a la funcin que el correspondiente al polinomio de Tay-
lor de grado 5. Se dice que se ha economizado en la serie de potencias
pues se obtien casi la misma precisin con menos trminos. Efecte
otro porceso de economizacin al polinomio resultante y estime el error
cometido.
2. La funcin arctan(r) puede representarse por la serie truncada de
potencias
arctan(r) = r
r
3
3
+
r
5
5

r
7
7
+
r
9
9
Economice tste polinomio tres veces a n de obtener un polinomio de
tercer grado. Trace la grca de los errores y comparela con los errores
del polinomio de grado 9.
3. Encuentre la aproximacin mediante funciones racionales (cuociente de
polinomios de grado 2) de la funcin
cos(r)
18
4 Integracin Numrica
La integracin numrica es el proceso mediante el cual se genera un valor
numrico para la integracin de una funcin sobre un conjunto. Por ejemplo:
_
2
0
c
x
2
dr
_
1
0
_
1
0
sin(rc
x
)drd
_
1
0
_
x
x
2
tan(r
2
)ddr
Estos problemas no son tratables con las tcnicas de los cursos bsicos de
Clculo.
En el caso
_
b
a
,(r)dr
la tcnica clsica consiste en encontrar la antiderivada, es decir, encontrar
1(r) tal que 1
0
= , y luego, por el Teorema Fundamental del Clculo
Integral, se tiene que
_
b
a
,(r)dr = 1(/) 1(c)
Sin embargo para la generalidad de los casos no es posible efectuar el pro-
ceso descrito. Una estrategia muy poderosa para calcular el valor numrico
de la integral consiste en reemplazar , por otra funcin q que aproxima
a , y que es fcil de integrar, de hecho, q puede ser un polinomio que
interpola a , en cierto conjunto de nodos. De este modo el valor de la inte-
gral debe ser una combinacin lineal del valor de la funcin en esos nodos,
ms an, con el objeto de simplicar los clculos, se puede suponer que los
nodos estn uniformemente espaciados, es decir r
0
= c, r
1
= c + /, . . .,
r
n
= c +:/ = /. As la frmula es del tipo:
_
b
a
,(r)dr -
n

i=0

i
,(r
i
)
Este tipo de aproximaciones se denominan Frmulas de Newton-Cotes. Como
hay : parmetros
i
es razonable esperar que una frmula de este tipo sea
19
exacta para polinomios de grado hasta :. Examinaremos algunos casos que
dan origen a frmulas clsicas.
4.1 Regla del Trapecio
En este caso : = 1 y los nodos son r
0
= c y r
1
= /. Adems sea
/ = / c, Entonces tendremos
_
b
a
,(r)dr -
0
,(c) +
1
,(c +/)
Adems podemos esperar que esta frmula sea exacta para polinomios de
grado 1, es decir, polinomios generados por 1 y r. Consideremos ambos
casos
1. Caso ,(r) = 1. En este caso obtenemos
_
b
a
1dr = / c = / =
0
1 +
1
1
2. Caso ,(r) = r. En este caso obtenemos
_
b
a
rdr =
1
2
(/
2
c
2
) =
/
2
(2c +/) =
0
c +
1
(c +/)
De esta manera obtenemos 2 ecuaciones para las dos incgnitas
0
y
1
Reemplazando la primera ecuacin en la segunda se obtiene:

0
+
1
= /

1
=
/
2
por lo tanto la frmula, para : = 1 es:
_
b
a
,(r)dr -
/
2
[,(c) +,(c +/)]
que es la conocida Frmula de los Trapecios. El error de la frmula es

1
12
(/ c)
3
,
00
(c)
donde c [c. /].
20
4.2 Regla de Simpson
Esta frmula se produce al considerar : = 2, en este caso hay tres nodos:
c, c +/, c +2/ donde / =
/ c
2
. La frmula en este caso debe ser de la
forma
_
b
a
,(r)dr -
0
,(c) +
1
,(c +/) +
2
,(c + 2/)
Como hay 3 parmetros es esperable que esta frmula sea exacta hasta grado
2. Para determinar los coecientes podemos estudiar el caso de 1, r, r
2
.
1. Veamos el caso ,(r) = 1. En esta situacin obtenemos
_
b
a
1dr = / c = 2/ =
0
1 +
1
1 +
2
1
2. Para ,(r) = r, obtenemos
_
b
a
rdr =
1
2
(/
2
c
2
) = 2/(c +/) =
0
c +
1
(c +/) +
2
(c + 2/)
3. Finalmente consideramos la funcin ,(r) = r
2
y obtenemos
_
b
a
r
2
dr =
1
3
(/
3
c
3
) = 2c
2
/+4c/
2
+
8
3
/
3
=
0
c
2
+
1
(c+/)
2
+
2
(c+2/)
2
Como en el caso anterior, reduciendo obtenemos las ecuaciones:

0
+
1
+
2
= 2/

1
+ 2
2
= 2/

1
+ 4
2
=
8
3
/
Lo que da la solucin
0
=
/
3
,
1
=
4/
3
,
2
=
/
3
, es decir, la frmula
obtenida es:
_
b
a
,(r)dr -
/
3
[,(c) + 4,(c +/) +,(c + 2/)]
que es conocida como la Regla de Simpson. Inesperadamente esta frmula
es exacta para polinomios de grado 3. El trmino de error asociado a la regla
de Simpson es

1
90
(/ c)
5
,
(4)
(c)
para algn c [c. /].
21
4.3 Cuadratura Gaussiana
Una sorpresiva variacin de los mtodos anteriores es considerar
_
b
a
,(r)n(r)dr -
n

i=0

i
,(n
i
)
donde n
i
no son los puntos equiespaciados del intervalo [c. /], y n(r) es
una funcin peso. En este caso contamos con : + 1 coecientes
i
y
con :+1 nodos n
i
por lo que podemos esperar que la frmula sea exacta
para polinomios de grado _ 2: + 1. Para demostrar esto se usa el siguiente
teorema de polinomios ortogonales.
Teorema: Consideremos una funcin n(r) de peso positiva y un
polinomio de grado : + 1 que sea ortogonal a todo polinomio j de grado
menor o igual a :, es decir
_
b
a
(r)j(r)n(r)dr = 0
Si n
0
, n
1
, . . ., n
n
, son las races de , entonces la frmula de cuadratura
es exacta para todo , polinomio de grado menor o igual a 2: + 1.
Demostracin: Sea , de grado menor o igual a 2: +1. Dividimos ,
por , obteniendo
, = j +:
donde j y : son polinomios de grado menor o igual n. En consecuencia
,(n
i
) = :(n
i
). Usando la ortogonalidad de , obtenemos
_
b
a
,ndr =
_
b
a
:ndr =
n

i=0

i
:(n
i
) =
n

i=0

i
,(n
i
)
lo que demuestra el teorema.
4.4 Cambio de Intervalos de Integracin
Supongamos que el intervalo de integracin es [c. /] , entonces para aplicar la
teora de polinomios ortogonales, es necesario cambiar el intervalo y pasar al
correspondiente a tipo de polinomios en que se desea trabajar. Supongamos
22
que se desea trabajar con los polinomios de Legendre, entonces el intervalo
de integracin debe ser [1. 1].
c 1
/ 1
r n
de ah se deduce que
r =
/ c
2
n +
/ +c
2
es el cambio de variable adecuada, adems dr =
/ c
2
dn. De este modo
obtenemos la igualdad
_
b
a
,(r)dr =
_
1
1
/ c
2
,
_
/ c
2
n +
/ +c
2
_
dn =
_
1
1
c(n)dn
Por lo tanto, sin restriccin, podemos considerar el problema de calcular
_
1
1
c(n)dn.
4.5 Polinomios Ortogonales
Existe una variedad de familias de polinomios ortogonales (una familia por
cada funcin peso n(r)).
En general las ms conocidas con sus pesos y sus intervalos son las sigu-
ientes
1. Polinomios de Legendre 1
j
(r): Funcin peso n(r) = 1, intervalo
[1. 1]. Algunos casos son:
1
0
(r) = 1
1
1
(r) = r
1
2
(r) =
3
2
r
2

1
2
1
3
(r) =
5
2
r
3

3
2
r
1
4
(r) =
35
8
r
4

15
4
r
2
+
3
8
1
5
(r) =
63
8
r
5

35
4
r
3
+
15
8
r
23
2. Polinomios de Laguerre 1
j
(r): Funcin Peso n(r) = c
x
, intervalo
[0. +). Algunos casos son
1
0
(r) = 1
1
1
(r) = 1 r
1
2
(r) = 1 2r +
1
2
r
2
1
3
(r) = 1 3r +
3
2
r
2

1
6
r
3
1
4
(r) = 1 4r + 3r
2

2
3
r
3
+
1
24
r
4
1
5
(r) = 1 5r + 5r
2

5
3
r
3
+
5
24
r
4

1
120
r
5
3. Polinomios de Hermite H
j
(r): Funcin Peso n(r) = c
x
2
, intervalo
(. +). Algunos casos son
H
0
(r) = 1
H
1
(r) = 2r
H
2
(r) = 4r
2
2
H
3
(r) = 8r
3
12r
H
4
(r) = 16r
4
48r
2
+ 12
H
5
(r) = 32r
5
160r
3
+ 120r
4. Polinomios de Chebyshev 1
j
(r): Funcin Peso n(r) = (1 r
2
)
1=2
,
intervalo [1. 1].
4.6 Cuadraturas de Gauss-Legendre
Ahora hacemos uso de las secciones anteriores para determinar frmulas de
integracin basadas en polinomios de Legendre. El procedimiento es debido
a Gauss y se aplica a variados polinomios ortogonales obteniendo frmulas
adecuadas para los diversos tipos de intervalos.
Supongamos que : = 1. Entonces tenemos la frmula
_
1
1
,(r)dr -
0
,(n
0
) +
1
,(n
1
)
24
que debe ser exacta para polinomios de grado menor o igual a 3, es decir
polinomios generados por 1, r, r
2
, r
3
. Examinemos los diversos casos:
1. Veamos el caso ,(r) = 1. En esta situacin obtenemos
_
1
1
1dr = 2 =
0
1 +
1
1
2. Para ,(r) = r, obtenemos
_
1
1
rdr = 0 =
0
n
0
+
1
n
1
3. En el caso ,(r) = r
2
y obtenemos
_
1
1
r
2
dr =
2
3
=
0
n
0
2
+
1
n
2
1
4. Finalmente consideramos el caso ,(r) = r
3
y obtenemos
_
1
1
r
3
dr = 0 =
0
n
0
3
+
1
n
3
1
Es decir, tenemos el sistema

0
+
1
= 2

0
n
0
+
1
n
1
= 0

0
n
0
2
+
1
n
2
1
=
2
3

0
n
0
3
+
1
n
3
1
= 0
Calculando la 4ta. Ec. menos la n
1
veces la 3ra. Ec. obtenemos
0
n
0
2
(n
0

n
1
) =
2
3
n
1
.
Calculando la 3ra. Ec. menos la n
1
veces la 2da. Ec. obtenemos
0
n
0
(n
0

n
1
) =
2
3
.
25
Calculando la 2da. Ec. menos la n
1
veces la 1ra. Ec. obtenemos
0
(n
0

n
1
) = 2n
1
. Es decir tenemos el sistema

0
(n
0
n
1
) = 2n
1

0
n
0
(n
0
n
1
) =
2
3

0
n
0
2
(n
0
n
1
) =
2
3
n
1
Dividiendo la 3ra. Ec. por la 2da. y luego la 2da. Ec. por la 1ra. tenemos
n
0
= n
1
n
0
=
1
3n
1
De donde se deduce que n
0
=
1
_
3
, n
1
=
1
_
3
.
0
=
1
= 1. As la
frmula de Gauss-Legendre para : = 1, es
_
1
1
,(r) - ,
_
1
_
3
_
+,
_

1
_
3
_
que es exacta para polinomios de hasta grado 3.
Ejercicios
1. Use las frmulas de los Trapecios, Simpson, para estimar la integral
,(r) = c
x
sin(r) sobre [1. 3] donde cada aplicacin tiene / = 1.
compare las aproximaciones y estime elerror cometido.
2. Demuestre las frmulas de los 3/8 y de Boole para integracin numrica.
3. Evale, mediante el mtodo de los trapecios, la integral de c
x
entre
r = 0 y r = 1 con un valor de / sucientemente pequeo para
garantizar exactitud de cinco decimales. cul es el tamao mximo de
/?
4. La Regla de Simpson es exacta para polinomios de grado 3. Esto se
explica porque el rea bajo cualquier cbica entre r = c y r = / es
identica al rea de una parbola que coincide con la cbica en r = c,
r = / y r = (c +/),2. Demuestre este hecho.
26
5. En los siguientes ejercicios, pruebe que las dos integrales son iguales
y calcule la aproximacin usando Cuadraturas de Gauss-Legendre de
orden 2:
(a)
_
2
0
6t
5
dt =
_
1
1
6(r + 1)
5
dr
(b)
1
_
2:
_
1
0
c
t
2
=2
dt =
1
_
2:
_
1
1
c
(x+1)
2
=8
dr
6. La Regla de Gauss-Legendre con tres nodos es:
_
1
1
,(r)dr -
1
9
_
5,
_

_
3
5
_
+ 8,(0) + 5,
_
_
3
5
__
Pruebe que la frmula es exacta para polinomios de grado hasta 5.
7. Deduzca la Regla de Gauss-Legendre con 3 puntos en [-1,1], usando el
hecho que los nodos son las races del Polinomio de Legrendre de grado
3:
r
1
=
_
3
5
. r
2
= 0. r
1
=
_
3
5
8. Calcule, mediante aproximacin numrica, usando el mtodo de los
trapecios para funciones de 2 variables, con : = : = 2, las siguientes
integrales:
(a)
_
1
0
_
2
0
2rdrd
(b)
_
1
0
_
1
0
c
(x
2
+y
2
)
drd
(c)
_
1
0
_
y
0
sin(r
2
+ 2
2
)drd
27
9. Elabore un mtodo, anlogo al de Simpson, para calcular integrales del
tipo
_
d
c
_
b
a
,(r. )drd
28
5 Ecuaciones Diferenciales Ordinarias
Las Ecuaciones Diferenciales aparecen naturalmente en la construccin de
modelos matemticos de problemas en ciencias e ingeniera. Normalmente
no existe una solucin analtica conocida por lo que hay que recurrir a aprox-
imaciones numricas.
Consideremos la siguiente situacin. Sea (t) la temperatura de un objeto
que se enfra. Se puede conjeturar que la velocidad de cambio de temperatura
del cuerpo est relacionada con la diferencia entre su temperatura y la del
medio ambiente, por medios experimentales se conrma esta conjetura y da
origen a la Ley de Newton que establece que dicha velocidad de cambio es
directamente proporcional a la diferencia de dichas temperaturas. Si deno-
tamos por la temperatura ambiente y por (t) la temperatura del cuerpo
en el instante t , entonces
d
dt
= /( ).
donde / es una constante positiva propia de la naturaleza del cuerpo. Si
concocemos la temperatura
0
del cuerpo en el instante t = 0, entonces
incluyendo esta condicin, llamada condicin inicial, obtenemos el siguiente
enunciado: Resolver
d
dt
= /( ) con (0) =
0
.
Mediante la tcnica de separacin de variables obtenemos
= + (
0
)c
kt
Cada eleccin de
0
nos proporciona una solucin distinta, en el Taller
veremos algunas grcos de las diferentes soluciones obtenidas.
En general un Problema de Valor Inicial

0
= ,(t. ) con (t
0
) =
0
en un intervalo [t
0
. /] es una funcin derivable = (t) tal que
(t
0
) =
0
e
0
(t) = ,(t. (t)) para todo t [t
0
. /]
29
Para visualizar geomtricamente el problema consideremos el rectngulo
1
1 = (t. )[ c _ t _ / , c _ _ d
En cada punto (t. ) del rectngulo se puede hallar la pendiente : de
la solucin = (t) mediante la frmula : = ,(t. (t)). Por lo tanto,
cada valor :
i;j
= ,(t
i
.
j
), representa la pendiente de la recta tangente a la
solucin que pasa por (t
i
.
j
), la grca de este proceso se denomina campo
de direcciones y puede usarse para ver cmo se va ajustando una solucin a
la sucesin de pendientes.
Algunos resultados clsicos de la teora son los siguientes:
Denicin: Dado el rectngulo 1, con , continua en 1, se dice que
la funcin , verica una condicin de Lipschitz con respecto a su variable
si existe una constante 1 0 tal que
[,(t.
1
) ,(t.
2
)[ _ 1[
1

2
[
para cualquier (t.
1
). (t.
2
) 1. La constante 1 se llama constante de
Lipschitz de ,.
Teorema: Supongamos que ,(t. ) est denida en 1. Si existe una
constante 1 0 tal que
[,
y
(t. )[ _ 1
para todo (t. ) 1, entonces , verica una condicin de Lipschitz con
respecto a su variable en 1, siendo 1 su constante de Lipschitz.
Teorema: (Existencia y Unicidad de soluciones) Supongamos que ,(t. )
es continua en 1. Si , verica una condicin de Lipschitz con respecto a
su variable y (t
0
.
0
) 1, entonces el problema de valor inicial tiene
solucin nica en algn subintervalo
0
_ t _ t
0
+o.
5.1 El Mtodo de la Serie de Taylor
Es un mtodo general y sirve de referencia para todos los dems mtodos.
Supongamos que (t) C
N+1
[t
0
. /] y que (t) tiene el desarrollo de
Taylor de orden ` alrededor de un punto t
k
[t
0
. /] dado por
(t
k
+/) = (t
k
) +
N

j=1

(j)
(t
k
)
,!
/
j1
+C(/
N+1
)
30
donde
(j)
(t) = ,
(j1)
(t. (t)) denota la derivada (, 1)-sima de la fun-
cin , respecto a t. Las frmulas de estas derivadas pueden calcularse
recursivamente usando la derivacin en cadena:

0
(t) = ,

00
(t) = ,
t
+,
y

0
= ,
t
+,
y
,

(3)
(t) = ,
tt
+ 2,
ty

0
+,
y

00
+,
yy
(
0
)
2
= ,
tt
+ 2,
ty
, +,
yy
,
2
+,
y
(,
t
+,
y
,)

(N)
(t) = 1
(N1)
,(t. (t))
donde 1 es el operador de derivacin
1 =
_
J
Jt
+,
J
J
_
El error global del mtodo es de orden C(/
N+1
), por lo tanto se puede elegir
` de manera que este error sea tan pequeo como se desee.
Este mtodo es poco prctico ya que hay que calcular derivadas parciales
de funciones y lo que desea es efectuar slo aplicaciones de , .Como se dijo
este mtodo sirve como referencia para determinar la calidad de otros mto-
dos.
5.2 El Mtodo de Euler
Sea [c. /] el intervalo en el que queremos hallar la solucin de un problema
de valor inicial
0
= ,(t. ) con (c) =
0
que est bien planteado (en
el sentido que , satisface una condicin de Lipschitz). Con los mtodos
numricos no vamos a encontrar una funcin derivable que sea solucin del
problema de valor inicial, en vez de eso, lo que se construye es un conjunto
nito de puntos (t
k
.
k
) que son aproximaciones de la solucin. Ms an,
es posible gracar este conjunto de puntos y as obtener una aproximacin
al grco de la solucin.
En primer lugar elegimos las abscisas de los puntos. Se divide el intervalo
[c. /] en ` subintervalos del mismo tamao, es decir
t
k
= c +// para / = 0. 1. . . . . `, siendo / =
/ c
`
El valor de / se llama tamao del paso.
31
Partiendo de t
0
, por el teorema de Taylor, tenemos
(t) = (t
0
) +
0
(t
0
)(t t
0
) +

00
(c
1
)(t t
0
)
2
2
para cierto c
1
[t
0
. t]. Sustituyendo
0
(t
0
) = ,(t
0
. (t
0
)) y / = t
1
t
0
, en
la ecuacin anterior, obtenemos
(t
1
) = (t
0
) +/,(t
0
. (t
0
)) +
00
(c
1
)
/
2
2
Si el tamao del paso / es sucientemente pequeo, entonces podemos des-
preciar el trmino que contiene /
2
y obtener
(t
1
) -
1
=
0
+/,(t
0
.
0
)
que se denomina aproximacin de Euler.
Repitiendo el proceso se genera una sucesin de puntos que se aproximana
la grca de la solucin buscada. El error del mtodo es del orden de /
1
Ejemplo: Usemos el mtodo de Euler para hallar una solucin aproxi-
mada del problema de valor inicial

0
= 1 en [0. 1] con (0) =
0
En este caso tenemos que

k+1
=
k
(1 +/1)
Por recursin obtenemos

M
=
0
(1 +/1)
M
=
0
_
(1 +/1)
1
hR
_
R
de modo que si / 0, entonces
M
= (1) =
0
c
R
lo que da una solucin
exacta.
5.3 El Mtodo de Heun
Se plantea un enfoque distinto para resolver el mismo problema que en la
seccin anterior.
32
Observemos que
_
t
1
t
0
,(t. (t))dt =
_
t
1
t
0

0
(t)dt = (t
1
) (t
0
).
Despejando (t
1
) obtenemos
(t
1
) = (t
0
) +
_
t
1
t
0
,(t. (t))dt
Usando la regla de los trapecios, con incremento / = t
1
t
0
, para estimar
la integral, se tiene
(t
1
) - (t
0
) +
/
2
[,(t
0
. (t
0
)) +,(t
1
. (t
1
))]
Como en el lado derecho aparece (t
1
) , que es lo que queremos calcular,
podemos usar una estimacin de este valor, para ello utilizamos la aproxi-
macin de Euler, de este modo se alcanza la siguiente frmula

1
= (t
0
) +
/
2
[,(t
0
.
0
) +,(t
1
.
0
+/,(t
0
.
0
))]
que se llama Mtodo de Heun.
El error global del mtodo es C(/
2
).
En general existe una gran variedad de mtodos y es posible sistemati-
zarlos en una gran familia.
5.4 Los Mtodos de Runge-Kutta
Los mtodos de Taylor tienen la caracterstica deseable de que el error global
es de orden C(/
N
), de modo que se puede escoge ` tan grande como se desee
para minimizar el error. Sin embargo tienen el inconveniente de tener que
determinar ` a priori y calcular las derivadas de orden superior de funciones
de varias variables lo que puede ser bastante complicado. Los Mtodos de
Runge-Kutta se construyen a partir de un mtodo de Taylor, de orden `, de
tal manera que el error global sea del orden C(/
N
) pero se evite la evaluacin
de las derivadas parciales; el precio a pagar es evaluar , en varios puntos,
pero sin duda este precio es bajo ante la perspectiva de evaluar derivadas
parciales. Desarrollaremos el caso ` = 1, ` = 2, y enunciaremos el caso
` = 4 que da origen al mtodo ms conocido de la familia.
33
5.4.1 Mtodo de Runge-Kutta de primer orden, ` = 1
En este caso el Mtodo de la Serie de Taylor es
(t
k
+/) = (t
k
) +/
0
(t
k
) +C(/
2
)
lo que coincide con el mtodo de Euler. De este modo tenemos que el mtodo
de Euler es un mtodo Runge-Kutta de primer orden.
5.4.2 Mtodo de Runge Kutta de segundo orden ` = 2
Escribiendo el desarrollo de Taylor para (t +/), tenemos
(t +/) = (t) +/
0
(t) +
1
2
/
2

00
(t) +C(/
3
)
Expresando
0
(t) e
00
(t) en trminos de , y sus derivadas parciales, obten-
emos
(t +/) = (t) +/,(t. ) +
1
2
/
2
[,
t
(t. ) +,
y
(t. ),(t. )] +C(/
3
)
En este mtodo se utiliza una combinacin lineal de dos funciones que
nos permita expresar
(t +/) = (t) +/,
0
+1/,
1
donde
,
0
= ,(t. ).
,
1
= ,(t +1/. +Q/,
0
)
Usando la frmula de Taylor para una funcin de dos variables podemos
aproximar ,(t. ) obteniendo la siguiente aproximacin de ,
1
,
1
= ,(t. ) +1/,
t
(t. ) +Q/,
y
(t. ),(t. ) +C(/
2
)
Sustituyendo en la expresin original de (t +/), obtenemos
(t +/) = (t)+(+1)/,(t. )+/
2
[11,
t
(t. ) +1Q,
y
(t. ),(t. )] +C(/
3
)
34
Comparando coecientes de los trminos correspondientes concluimos que
+1 = 1
11 =
1
2
1Q =
1
2
Tenemos 3 ecuaciones y 4 incgnitas, con 1, 1, Q distintos de 0, lo que
nos permite elegir libremente uno de los coecientes
1. Caso = 1,2. Esto implica que 1 = 1,2, 1 = 1, Q = 1. De este
modo obtenemos la frmula
(t +/) = (t) +
1
2
/[,(t. ) +,(t +/. +/,(t. ))]
que es el Mtodo de Heum o Mtodo Mejorado de Euler.
2. Caso = 0. Esto implica que 1 = 1, 1 = 1,2, Q = 1,2. Escribiendo
la ecuacin con estos parmetros obtenemos
(t +/) = (t) +/,
_
t +
/
2
. +
/
2
,(t. )
_
Este mtodo se denomina Mtodo Modicado de Euler o Mtodo de
Cauchy.
Evidentemente hay innitos mtodos de segundo orden, sin embargo los
dos mencionados son clsicos en la literatura.
5.4.3 Mtodo de Runge Kutta de cuarto orden ` = 4
Este mtodo, denominado RK4, simula la presicin del mtodo de la serie de
Taylor de orden ` = 4 y consiste en calcular la aproximacin
k+1
de la
siguiente manera:

k+1
=
k
+n
1
/
1
+n
2
/
2
+n
3
/
3
+n
4
/
4
.
35
donde /
1
, /
2
, /
3
, /
4
son de la forma
/
1
= /,(t
k
.
k
).
/
2
= /,(t
k
+c
1
/.
k
+/
1
/
1
).
/
3
= /,(t
k
+c
2
/.
k
+/
2
/
1
+/
3
/
2
).
/
4
= /,(t
k
+c
3
/.
k
+/
4
/
1
+/
5
/
2
+/
6
/
3
).
Al igual que en el mtodo de segundo orden, se pueden comparar coecientes,
de este Runge y Kutta obtuvieron el siguiente sistema de ecuaciones:
/
1
= c
1
.
/
2
+/
3
= c
2
.
/
4
+/
5
+/
6
= c
3
.
n
1
+n
2
+n
3
+n
4
= 1.
n
2
c
1
+n
3
c
2
+n
4
c
3
=
1
2
.
n
2
c
2
1
+n
3
c
2
2
+n
4
c
2
3
=
1
3
.
n
2
c
3
1
+n
3
c
3
2
+n
4
c
3
3
=
1
4
.
n
3
c
1
/
3
+n
4
(c
1
/
5
+c
2
/
6
) =
1
6
.
n
3
c
1
c
2
/
3
+n
4
c
3
(c
1
/
5
+c
2
/
6
) =
1
8
.
n
3
c
2
1
/
3
+n
4
(c
2
1
/
5
+c
2
2
/
6
) =
1
12
.
n
4
c
1
/
3
/
6
=
1
24
.
Este sistema tiene 11 ecuaciones con 13 incgnitas, as es que podemos aadir
dos condiciones extras para resolverlo. La eleccin ms til es
c
1
=
1
2
y /
2
= 0.
Los dems valores de la solucin son
c
2
=
1
2
. c
3
= 1. /
1
= /
3
=
1
2
/
4
= /
5
= 0, /
6
= 1,
n
1
=
1
6
. n
2
=
1
3
. n
3
=
1
3
. n
4
=
1
6
.
36
De este modo el Mtodo de Runge-Kutta de orden 4 usa la frmula recursiva

k+1
=
k
+
/
6
[,
1
+ 2,
2
+ 2,
3
+,
4
]
donde
,
1
= ,(t
k
.
k
).
,
2
= ,(t
k
+
/
2
.
k
+
/
2
,
1
).
,
3
= ,(t
k
+
/
2
.
k
+
/
2
,
2
).
,
4
= ,(t
k
+/.
k
+/,
3
).
Ejercicios
1. Considere el problema de valor inicial

0
= 0.12
en [0. 5] con (0) = 1000.
(a) Aplique la frmula de Euler para calcular (5), tomando como
pasos / = 1, / = 1,2.
(b) Cul es el lmite cuando / tiende a cero?
2. Crecimiento exponencial de una poblacin. La poblacin de ciertas es-
pecies crece a una velocidad que es proporcional a la poblacin presente
y que responde a un problema de valor inicial como el siguiente:

0
= 0.02 en [0. 5] con (0) = 5000
(a) Aplique la frmula de Euler para calcular la poblacin (5) us-
ando pasos / = 1, / = 1,2.
(b) Cul es el lmite cuando / tiende a cero?
3. Un paracaidista salta desde un avin. Hasta el momento en que abre el
paracadas, la resistencia del aire es proporcional a
3=2
( representa
la velocidad). Supongamos que el intervalo de tiempo es [0. 6] y que
la ecuacin diferencial para la velocidad de descenso es

0
= 10 0.01
3=2
en [0. 6] con (0) = 0.
Use el mtodo de Euler con / = 0.1 para estimar (6).
37
4. Modelo de una Epidemia. Supongamos que tenemos una comunidad
de 1 personas que contiene inicialmente 1 personas contagiadas y
Q sin contagiar. Sea (t) el nmero de personas contagiadas en un
instante t. Si la enfermedad no es muy grave, como el resfriado comn,
contina activo y la epidemia se extiende. Puesto que hay 1Q posibles
contactos entre personas de uno y otro grupo, la velocidad de cambio
de (t) es proporcional a 1Q, as que el problema puede modelarse
mediante el problema de valor inicial

0
= /(1 ) con (0) =
0
(a) Tomando 1 = 25000, / = 0.00003 y / = 0.2 con la condicin
inicial (0) = 250, use el programa correspondiente para calcular
la aproximacin de Euler en el intervalo [0. 60].
(b) Dibuje la grca de la solucin aproximada.
(c) Estime el nmero medio de personas contagiadas calculando el
promedio de las ordenadas obtenidas.
5. En los siguientes ejercicios resuelva la Ecuacin Diferencial usando el
Mtodo de Heun.
(a) Tome / = 0.2 y d dos pasos calculando los valores a mano.
Luego tome / = 0.1 y d cuatro pasos calculando los valores a
mano.
(b) Compare la solucin exacta (0.4) con las dos aproximaciones
calculadas antes.
(c) Se comporta el error global nal de las aproximaciones obtenidas
en (a) como se espera cuando / se divide entre dos?
1.
0
= t
2
con (0) = 1, (t) = c
t
+t
2
2t + 2
2.
0
= 3 + 3t con (0) = 1, (t) =
4
3
c
3t
t
1
3
3.
0
= c
2t
2 con (0) = 1,10, (t) = c
2t
+tc
2t
4.
0
= 2t
2
con (0) = 1, (t) = 1,(1 t
2
)
38
6. Pruebe que cuando se usa el Mtodo de Heun para resolver el problema
de valor inicial
0
= ,(t) en [c. /] con (c) =
0
= 0 el resultado
es
(/) =
/
2
M1

k=0
(,(t
k
) +,(t
k+1
)) .
que es la aproximacin dada por la regla del Trapecio para aproximar
la integral denida de ,(r) en el intervalo [c. /].
7. Pruebe que el Mtodo de Heun falla cuando queremos aproximar la
solucin (t) = t
3=2
del problema de valor inicial

0
= ,(t. ) = 1.5
1=3
con (0) = 0.
Justique sus respuesta. Cul es el problema?
8. Consideremos un proyectil que se dispara hacia arriba y luego cae si-
guiendo una trayectoria rectilinea. Si la resistencia del aire es pro-
porcional a la velocidad, entonces el problema de valor inicial para la
velocidad (t) es

0
= 10
1
`
con (0) =
0
.
siendo
0
la velocidad inicial, ` la masa y 1 el coeciente de
resistencia del aire. Supongamos que
0
= 40 m/s y 1,` = 0.1 .
Use el Mtodo de Heun con / = 0.5 para resolver el problema de valor
inicial

0
= 10 0.1 en [0. 4] con (0) = 40.
Dibuje su solucin y la solucin exacta (t) = 140c
t=10
100 en una
misma grca.
9. En los siguientes ejercicios resuelva la ecuacin diferencial usando el
Mtodo Runge-Kutta de orden ` = 4.
(a) Tome / = 0.2 y d dos pasos calculando los valores a mano. Luego,
tome / = 0.1 y d cuatro pasos calculando los valores a mano.
(b) Compare la solucin exacta (0.4) con las dos aproximaciones
calculadas en (a).
39
(c) Se comporta el error global nal de las aproximaciones obtenidas
en (a) como se espera cuando / se divide entre dos?
1.
0
= t
2
con (0) = 1, (t) = c
t
+t
2
2t + 2
2.
0
= 3 + 3t con (0) = 1, (t) =
4
3
c
3t
t
1
3
3.
0
= c
2t
2 con (0) = 1,10, (t) = c
2t
+tc
2t
4.
0
= 2t
2
con (0) = 1, (t) = 1,(1 t
2
)
10. Pruebe que cuando se usa el Mtodo de Runge-Kutta de orden 4 para
resolver el problema de valor inicial
0
= ,(t) en [c. /] con (c) =

0
= 0 el resultado es
(/) =
/
6
M1

k=0
_
,(t
k
) + 4,(t
k+1=2
) +,(t
k+1
)
_
.
donde / = (/c),`, t
k
= c+// y t
k+1=2
= c+(/+1,2)/, que es la
aproximacin dada por la regla de Simpson para aproximar la integral
denida de ,(r) en el intervalo [c. /].
11. En una reaccin qumica, una molcula de una sustancia se combina
con una molcula de una sustancia 1 para formar una molcula de una
sustancia C. Se sabe que la concentracin (t) de la sustancia C en
el instante t es la solucin del problema de valor inicial

0
= /(c )(/ ) con (0) = 0.
donde / es una constante positiva y c y / son las concentraciones
iniciales de las sustancias y 1, respectivamente. Supongamos
que / = 0.01, c = 70 milimoles/litro y / = 50 milimoles/litro. Use
el Mtodo de Runge-Kutta de orden 4 con / = 0.5 para hallar la
solucin en el intervalo [0. 20]. Compare su resultdo con la solucin
exacta (t) = 350(1 c
0:2t
),(7 5c
0:2t
).
12. En los siguientes problemas tome / = 0.05 y use
(a) El Mtodo de Euler
(b) El Mtodo de Runge-Kutta
40
1 Para resolver el sistema
r
0
= 2r + 3

0
= 2r +
r(0) = 2.7 (0) = 2.8
en el intervalo [0. 10]. Compare con la solucin exacta
r(t) =
69
25
c
t
+
3
50
c
4t
(t) =
69
25
c
t
+
1
25
c
4t
2 Para resolver el sistema
r
0
= 3r

0
= 4r
r(0) = 0.2 (0) = 0.5
en el intervalo [0. 2]. Compare con la solucin exacta
r(t) =
1
5
c
t

1
10
tc
t
(t) =
1
2
c
t

1
5
tc
t
13. Para resolver ecuaciones diferenciales de orden superior podemos usar el
siguiente mtodo (en este caso el orden es 2). Consideremos la ecuacin
r
00
(t) = ,(t. r(t). r
0
(t)) con r(t
0
) = r
0
y r
0
(t
0
) =
0
Esta ecuacin diferencial de segundo orden puede reformularse como
un sistema con dos ecuaciones de primer orden usando la sustitucin
r
0
(t) = (t).
Entonces r
00
(t)
0
(t) y la ecuacin diferencial anterior se convierte en el
sistema
dr
dt
=
d
dt
= ,(t. r. )
r(t
0
) = r
0
(t
0
) =
0
Usando lo anterior, en los siguientes problemas:
41
(a) Reformule la ecuacin diferencial de segundo orden como un sis-
tema de dos ecuaciones de primer orden.
(b) Use el programa RK4 para resolver cada sistema en el intervalo
[0. 2] tomando como tamao de paso / = 0.05.
(c) Dibuje la aproximacin obtenida y la solucin exacta en una misma
grca.
1.-
2r
00
(t) 5r
0
(t) 3r(t) = 45c
2t
con r(0) = 2 y r
0
(0) = 1
Sol : r(t) = 4c
t=2
+ 7c
3t
9c
2t
2.-
r
00
(t) + 6r
0
(t) + 9r(t) = 0 con r(0) = 4 y r
0
(0) = 4
Sol : r(t) = 4c
3t
+ 8tc
3t
3.-
r
00
(t) +r
0
(t) = 6 cos(t) con r(0) = 2 y r
0
(0) = 3
Sol : r(t) = 2 cos(t) + 3 sin(t) + 3t sin(t)
4.-
r
00
(t) + 3r
0
(t) = 12 con r(0) = 5 y r
0
(0) = 1
Sol : r(t) = 4 + 4t +c
3t
14. Un cierto sistema resonante de muelles sobre el que se ejerce una fuerza
externa peridica se modela mediante la ecuacin
r
00
(t) + 25r(t) = 8 sin(5t) con r(0) = 0 y r
0
(0) = 0
Use el mtodo de Runge-Kutta para resolver la ecuacin diferencial en
el intervalo [0. 2] usando ` = 40 pasos con / = 0.05.
15. El modelo predador-presa. Un ejemplo de un sistema de ecuaciones
diferenciales no lineales es el problema predador-presa. En un cierto
42
hbitat viven conejos y linces, cuyas poblaciones en un instante t de-
notamos por r(t) e (t), respectivamente. El modelo predador-presa
establece que r(t) e (t) verican el sistema
r
0
(t) = r(t) 1r(t)(t).

0
(t) = Cr(t)(t) 1r(t).
Una simulacin tpica con un computador usara como coecientes, por
ejemplo,
= 2. 1 = 0.02. C = 0.0002. 1 = 0.8.
Use el mtodo de Runge-Kutta para resolver el sistema en el intervalo
[0. 5] usando ` = 40 pasos con / = 0.2 en los siguientes casos
(a) r(0) = 3000 conejos e (0) = 120 linces.
(b) r(0) = 5000 conejos e (0) = 100 linces.
16. Resuelva
r
0
= r r.

0
= +r
con r(0) = 4 e (0) = 1
en [0. 8] tomando / = 0.1. Las trayectorias de este sistema son curvas
cerradas.
43