FHMM1034 Mathematics III

Centre For Foundation Studies

Department of Sciences and Engineering
FHMM1034 Mathematics III
Chapter 1
Coordinate Geometry
FHMM1034
Mathematics III
1
Coordinate Geometry
Topics
1.1 The Cartesian Coordinate
1.2 The Straight Line
1.3 Shortest Distance from a Point to a
Straight Line
1.4 Circle
FHMM1034
Mathematics III
2
1.4 Circle
1.5 Intercepts and intersections
1.6 Parabola
Topics
1.7 Ellipse
1.8 Hyperbola
1.9 Shifted Conics
FHMM1034
Mathematics III
3
1.10 Parametric Equations
1.11 Loci
1.1 1.1
The Cartesian
Coordinate
FHMM1034
Mathematics III
4
Coordinate
Cartesian Coordinate
y
0
x

a
b
P(a, b)
FHMM1034
Mathematics III
5
0
5
y
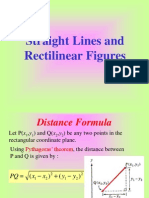
Distance between 2 points
plane. coordinate
on the ) , ( and ) , ( points Let
2 2 1 1
y x Q y x P
y
Q(x
2
, y
2
)
2 1
y y
2
y
plane. coordinate
FHMM1034
Mathematics III
6
0
x
P(x
1
, y
1
)
6
2 1
x x
2
x
1
x
2 1
1
y
R(x
2
, y
1
)
Distance between 2 points
The Pythagorean Theorem gives
DISTANCE FORMULA
2 2
2 1 2 1
PQ x x y y = +
2 2
2 1 2 1
( ) ( ) x x y y = +
FHMM1034
Mathematics III
7
( ) ( )
1 1 2 2
2 2
2 1 2 1
DISTANCE FORMULA
The distance for ( , ) and ( , ) is

P x y Q x y
x x y y +
7
Example 1
Which of the points P(1, 2) or Q(8, 9) is
closer the point A(5, 3) ? closer the point A(5, 3) ?
FHMM1034
Mathematics III
8
Example 2
of distance the Find plane. coordinate on the
points three are ) , 3 ( and ) 1 , 4 ( , ) 5 , 2 (
2
5
C B A
area. its find and triangle angled - right a
is that show Hence, . and ,
of distance the Find plane. coordinate on the
ABC AC BC AB
FHMM1034
Mathematics III
9
Point Dividing Straight Line
internally ) , ( point and ) , (
point joining line the divides ) , ( If
y x Q y x P
y x R
then , : ratio in the
internally ) , ( point and ) , (
2 2 1 1

y x Q y x P




+
+
=
+
+
=
1 2 1 2
,
y y
y
x x
x
FHMM1034
Mathematics III
10
+ +
Point Dividing Straight Line
, externally line the divides ) , ( If PQ y x R
then , signs opposite have will and

=
1 2 1 2
,
y y
y
x x
x
FHMM1034
Mathematics III
11

Example 3
point the and ) 3 , 8 ( point the joining line the
divides which point the of s coordinate the Find
P
R
internally (i)
2 : 5 ratio in the ) 5 , 4 (
point the and ) 3 , 8 ( point the joining line the
Q
P
FHMM1034
Mathematics III
12
externally (ii)
Point Dividing Straight Line
FHMM1034
Mathematics III
13
R divides PQ internally. R divides PQ externally.
Mid-Point
and ) , ( point of point - mid The
1 1
y x P
are ) , ( point
2 2
1 1
y x Q

+ +
2
,
2
2 1 2 1
y y x x
FHMM1034
Mathematics III
14

2 2
Example
Show that the quadrilateral with vertices
(1, 2), (4, 4), (5, 9) and (2, 7) is a
paralelogram by proving that its two
diagonals bisect each other.
P Q R S
FHMM1034
Mathematics III
15 15
1.2 1.2
The Straight Line
FHMM1034
Mathematics III
16
Straight Line
passing line straight a of slope gradient / The m
is ) , ( and ) , ( points through
2 2 1 1
y x Q y x P
2 1
1 2
1 2
, x x
x x
y y
m

=
FHMM1034
Mathematics III
17
1 2
x x
The Equation of Straight Line
is ) , ( and ) , ( points
through passing line straight a of equation The
2 2 1 1
y x B y x A is ) , ( and ) , ( points
2 2 1 1
y x B y x A
1 2
1 2
1
1
x x
y y
x x
y y

FHMM1034
Mathematics III
18
1 2 1
x x x x
The Equation of Straight Line
is ) , ( point he through t passing and
gradient with line straight a of equation The
b a
m
is ) , ( point he through t passing and b a
) ( a x m b y =
FHMM1034
Mathematics III
19
Example 4
). 3 , 5 ( and ) 2 , 4 ( points e through th
passing line straight the of equation the Find
K H ). 3 , 5 ( and ) 2 , 4 ( points e through th K H
FHMM1034
Mathematics III
20
Example 5
with line straight the of equation the Find
). 5 , 1 ( points throught passes that
3
2
gradient
FHMM1034
Mathematics III
21
Parallel and Perpendicular Lines
and angles at inclined are which , and
lines the of gradients the represent and Let
2 1 2 1
2 1
l l
m m
. tan and tan Then,
axis. positive the ly to respective
and angles at inclined are which , and
2 2 1 1
2 1 2 1


= =

m m
x
l l
parallel. are and lines two the , If (i)
2 1 2 1
l l m m =
FHMM1034
Mathematics III
22
lar. perpendicu
are and lines two the , 1 If (ii)
2 1 2 1
l l m m =
Example
(a) Find an equation of the line through
the point (5, 2) that is parallel to the the point (5, 2) that is parallel to the
line 4 6 5 0.
(b) Find an equation of the line that is
x y + + =
FHMM1034
Mathematics III
23
(b) Find an equation of the line that is
perpendicular to the line 4 6 5 0
an
x y + + =
d passes through the origin.
Angle Between 2 Lines
by given is
and lines two e between th angle The
2 1
l l
by given is
2 1
1 2
1
tan
m m
m m
+

l
FHMM1034
Mathematics III
24
angle. obtuse an is , 0 tan If (ii)
angle. acute an is , 0 tan If (i)


<
>
1
l
2
l
Example 6
lines straight e between th angle the Find
. 0 20 3 5 and 0 8 4 3 = + = + y x y x
FHMM1034
Mathematics III
25
1.3
Shortest Distance Shortest Distance
from a Point to a
Straight Line
FHMM1034
Mathematics III
26
Straight Line
The Shortest Distance
is 0 line straight the to
) , ( point a from distance shortest The
= + + c by ax
k h P d
is 0 line straight the to = + + c by ax
2 2
b a
c bk ah
d
+
+ +
=
the of side same on the lying ) , ( points For k h
i i
FHMM1034
Mathematics III
27
ve). or ve (either sign same have all
s expression the , 0 line straight
the of side same on the lying ) , ( points For
+ + +
= + +
c bk ah
c by ax
k h
i i
i i
Example 7
line straight the to ) 4 , 2 ( point the
from distance lar perpendicu the Find
P
. 0 5 4 3
line straight the to ) 4 , 2 ( point the
= +

y x
P
FHMM1034
Mathematics III
28
Example 8
on lie ) 2 , ( and ) , 2 ( points the
if determine diagram, a using Without
Q P
. 0 4 2
line straight the of side same the
on lie ) 2 , ( and ) , 2 ( points the
2
1
2
1
= + y x
Q P
FHMM1034
Mathematics III
29
1.4 1.4
Circle
FHMM1034
Mathematics III
30
Circle
is radius and
) , ( centre with the circle a of equation The
r
b a C
is radius and r
2 2 2
) ( ) ( r b y a x = +
: becomes equation the origin, the is centre the If
FHMM1034
Mathematics III
31
: becomes equation the origin, the is centre the If
2 2 2
r y x = +
Circle
: is circle a of equation general The
0 2 2
2 2
= + + + + c fy gx y x
. is radius its
and ) , ( is centre its where
2 2
c f g
f g
+

FHMM1034
Mathematics III
32
. is radius its
2 2
c f g +
Example 9
circle the of equation an Find
). 5 , 2 ( center and 3 radius with
FHMM1034
Mathematics III
33
Example 10
the has that circle the of equation an Find
diameter. the of
endpoints the as ) 6 , 5 ( and ) 8 , 1 ( point
the has that circle the of equation an Find
Q P
FHMM1034
Mathematics III
34
Example 11
of graph that the Show
radius. and centre its find and circle, a is
0 9 ) 3 4 ( 2
2 2
= + + + x y y x
FHMM1034
Mathematics III
35
Example 12
at the centre with circle the of equation the Find
. 6 3 2
line the from centre the of distance shortest
the to equal radius having and ) 2 , 3 ( point
at the centre with circle the of equation the Find
+ = x y
36
Example 13
) 1 , 5 ( point at the tangent the of equation the Find
. 0 20 4 2 circle on the
) 1 , 5 ( point at the tangent the of equation the Find
2 2
= + + y x y x
37
Example 14
) 2 , 4 ( point the of distance lar perpendicu the Find A
line. above the touches circle the where
point the of s coordinate the also Find . 4 2 line
straight the touching ) 2 , 4 ( centre with circle a of
equation the find Then, . 4 2 line straight the to
= +
= +
y x
A
y x
38
line. above the touches circle the where
1.5 1.5
Intercepts and
intersections
FHMM1034
Mathematics III
39
intersections
The x-coordinates of the points where a graph
intersects the x-axis are called the x-intercepts of
Intercepts
intersects the x-axis are called the x-intercepts of
the graph and y = 0.
The y-coordinates of the points where a graph
FHMM1034
Mathematics III
40
intersects the y-axis are called the y-intercepts of
the graph and x = 0.
Intercepts
FHMM1034
Mathematics III
41
Set y =0 and solve for x Set x = 0 and solve for y
Find the xintercepts and yintercept of the
equation
Example 15
2
=
equation
. 2
2
= x y
FHMM1034
Mathematics III
42
In general, the coordinate of the points of
intersection of two equations can be found by
Points of Intersection
intersection of two equations can be found by
solving the two equations simultaneously.
Each real solution gives a point of intersection.
FHMM1034
Mathematics III
43
(i) 2 distinct real roots
(ii) 2 equal real roots
Types of Points of Intersection
(ii) 2 equal real roots
(iii) No real roots
FHMM1034
Mathematics III
44
(i) (ii)
(iii)
Example 16
Find the coordinates of all points of intersection
between the curves in each of the following
x x x y x y
y y x x y
6 5 , 2 (ii)
0 3 3 , 3 2 (i)
2 3
2 2
+ + = =
= + = +
between the curves in each of the following
cases.
FHMM1034
Mathematics III
45
Example 17
and 24 2 of graphs Sketch the x y = +
. of point - mid the of s coordinate the find
, and of s coordinate the finding Without
. and on, intersecti of points mark the and
diagram, same on the 10 6
and 24 2 of graphs Sketch the
2
PQ
Q P
Q P
x x y
x y
+ =
= +
FHMM1034
Mathematics III
46
. of point - mid the of s coordinate the find PQ
1.6 1.6
Parabola
FHMM1034
Mathematics III
47
Parabola
A parabola is the set of points in the plane
equidistant from a fixed point F (called the focus) equidistant from a fixed point F (called the focus)
and a fixed line l (called the directrix).
FHMM1034
Mathematics III
48 FHMM1034
Mathematics III
48
F(0,a)
y = - a
a
a
Parabola
is parabola a of equation general The
ay x 4
2
=
vertex. the called is (0,0)
directrix. the called is line fixed the
and focus the called is ) , 0 ( point fixed The
= a y
a F
FHMM1034
Mathematics III
49
. 0 for only exists
and axis about symmetric is graph The
vertex. the called is (0,0)

y
y
If a>0 opens upward If a<0 opens downward
Parabola
(0, a)
FHMM1034
Mathematics III
50
(0, a)
Parabola
Parabola with vertical
axis
Parabola with horizontal
axis axis
Equation :
Properties: Vertex V (0,0)
Focus F (0, a)
Directrix y = - a
axis
Equation:
Properties: Vertex V (0,0)
Focus F (a, 0)
Directrix x = - a
ay x 4
2
=
ax y 4
2
=
FHMM1034
Mathematics III
51
Parabola
The line segment that
run through the focus
a a
run through the focus
perpendicular to the
axis with endpoints on
the parabola is called
the latus rectum and
a a
2a
F(a, 0)
FHMM1034
Mathematics III
52
the latus rectum and
its length is the focal
diameter.
F(a, 0)
x = -a
Example 18
a) Find the equation of the parabola with vertex
V(0 ,0) and focus F(0, 2), and sketch its graph. V(0 ,0) and focus F(0, 2), and sketch its graph.
b) Find the focus and directrix of the parabola
and sketch the graph.
c) Find the focus, directrix and focal diameter of
0 6
2
= + y x
FHMM1034
Mathematics III
53
c) Find the focus, directrix and focal diameter of
the parabola and sketch its graph.
2
2
1
x y =
1.7 1.7
Ellipse
FHMM1034
Mathematics III
54
An ellipse is the set of all points in the plane the
sumof whose distances from 2 fixed points.
Ellipse
sumof whose distances from 2 fixed points.
These 2 fixed points are the foci of the ellipse.
y
P(x, y)
FHMM1034
Mathematics III
55
x
0 F1(-c,0) F2(c,0)
Ellipse
is ellipse an of equation general The
1
2
2
2
2
= +
b
y
a
x
axis major the called is 2 and Generally, a b a >
FHMM1034
Mathematics III
56
axis. minor the called is 2 and
axis major the called is 2 and Generally,
b
a b a >
Ellipse
FHMM1034
Mathematics III
57
Ellipse
1
2
2
2
2
= +
a
y
b
x
1
2
2
2
2
= +
b
y
a
x
Equation: Equation:
0 > > b a
a b
0 > > b a
a
a
c
2 2 2
b a c =
c
2 2 2
b a c =
c
e =
c
e =
Vertices: ( , 0)
Major axis: 2a
Minor axis: 2b
Foci: ( ,0) ,
Eccentricity,
Vertices: ( 0, )
Major axis: 2a
Minor axis: 2b
Foci: (0, ) ,
Eccentricity,
FHMM1034
Mathematics III
58
a
c
e =
a
c
e =
Eccentricity, Eccentricity,
Eccentricity of an ellipse, e
The eccentricity is a measure of how stretched
Ellipse
The eccentricity is a measure of how stretched
the ellipse is.
Eccentricity of an ellipse,
The eccentricity of every ellipse satisfies
.
a
c
e =
. 1 0 < < e
FHMM1034
Mathematics III
59
The eccentricity of every ellipse satisfies
If e is close to 1, the ellipse is elongated in
shape but if e is close to 0 then the ellipse is
close to a circle in shape.
. 1 0 < < e
Example 19
: ellipse an
represent equations following the of each that Show
8 4 (ii)
4 2 (i)
: ellipse an
2 2
2 2
= +
= +
y x
y x
FHMM1034
Mathematics III
60
curves. sketch the and case, each properties the all State
Example 20
a) Find the equation of an ellipse with its
vertices are and the foci are . ) 0 , 4 (
) 0 , 2 ( vertices are and the foci are .
b) Find the equation of the ellipse with foci
and eccentricity .
5
4
= e
) 0 , 4 (
) 0 , 2 (
) 8 , 0 (
FHMM1034
Mathematics III
61
5
Example 21
, 6 3 2
2 2
= + y x
Find the equations of the tangents with gradient 2
to the ellipse with equation and
, 6 3 2
2 2
= + y x
to the ellipse with equation and
find their points of intersection.
FHMM1034
Mathematics III
62
1.8 1.8
Hyperbola
FHMM1034
Mathematics III
63
Hyperbola
A hyperbola is the set of all points in the plane,
the difference of whose distances from 2 fixed the difference of whose distances from 2 fixed
points. These fixed points are the foci of the
hyperbola.
y
P (x, y)
FHMM1034
Mathematics III
64
x
0
F2 (c, 0) F1 (-c, 0)
Hyperbola
is hyperbola a of equation general The
1
2
2
2
2
=
b
y
a
x
: that Note
FHMM1034
Mathematics III
65
. for exist not does curve The
: that Note
a x a < <
Hyperbola
ve) or ve (either of value large For
: Notice
x +
: i.e.
ve) or ve (either of value large For
2
2
2
2
x
a
b
y
x
a
b
y
x
x

+
FHMM1034
Mathematics III
66
. asymptotes the are Hence, x
a
b
y
x
a
y
=

Hyperbola
FHMM1034
Mathematics III
67
1
2
2
2
2
=
b
y
a
x
Equation :
Equation:
Hyperbola
1
2
2
2
2
=
b
y
a
x
1
2
2
2
2
=
b
x
a
y
Vertices ( ,0)
Asymptotes
Foci ( ,0) ,
Vertices (0, )
Asymptotes
Foci (0, ) ,
b a
a
x
a
b
y =
a
b a
x
b
a
y =
c
2 2 2
b a c + = c
2 2 2
b a c + =
FHMM1034
Mathematics III
68
The Rectangular Hyperbola
: If b a =
to reduces hyperbola a of equation The
2 2 2
a y x =
hyperbola, r rectangula the called is hyperbola This
FHMM1034
Mathematics III
69
. are asymptotes with the
hyperbola, r rectangula the called is hyperbola This
x y =
The Rectangular Hyperbola
The graph of and
are shown below
2 2 2
a y x =
2
c xy =
are shown below
2 2 2
a y x =
y
2
c xy =
FHMM1034
Mathematics III
70
x
0
Example 22
: curves following e Sketch th
2 2
y x
5 (ii)
1
4 9
(i)
2 2
2 2
=
=
y x
y x
FHMM1034
Mathematics III
71
4 ) 1 ( (iii) = y x
Example 23
a) State all the properties of the hyperbola and
sketch the graph sketch the graph
b) Find the equation of the hyperbola with
vertices and foci .
0 9 9 (ii) 144 16 9 (i)
2 2 2 2
= + = y x y x
) 0 , 4 ( ) 0 , 3 (
FHMM1034
Mathematics III
72
c) Find the equation of the hyperbola with
vertices and asymptotes . ) 2 , 0 ( 2 = y
1.9 1.9
Shifted Conics
FHMM1034
Mathematics III
73
In previous section, we studied parabolas with
vertices at the origin and ellipse and hyperbolas
Shifted Conics
vertices at the origin and ellipse and hyperbolas
with centers at origin.
In this section, we consider conics whose
vertices and centers are not necessarily at the
FHMM1034
Mathematics III
74
vertices and centers are not necessarily at the
origin, and we need to determine how this affects
their equations.
Shifted Conics
Given h and k are positive real numbers,
Replacement How the graph is shifted
1. x replaced by x h
2. x replaced by x + h
3. y replaced by y k
Right h units
Left h units
Upward k units
FHMM1034
Mathematics III
75
(Page 776)
3. y replaced by y k
4. y replaced by y + k
Upward k units
Downward k units
Shifted Ellipses
General equation of an ellipse:
2 2
y x
If we shift it so that its center is at the point (h, k)
instead of at the origin, then its equation
1
2
2
2
2
= +
b
y
a
x
FHMM1034
Mathematics III
76
becomes:
1
) ( ) (
2
2
2
2
=

b
k y
a
h x
Shifted Ellipses
FHMM1034
Mathematics III
77
(Page776)
Sketch the graph of the ellipse
Example 24
and determine the center.
1
9
) 2 (
4
) 1 (
2 2
=

+
+ y x
FHMM1034
Mathematics III
78
Applying shifts to parabolas leads to the
equations and graphs shown as followings:
Shifted Parabolas
equations and graphs shown as followings:
FHMM1034
Mathematics III
79
0 for
) ( 4 ) ( ) i (
2
>
=
a
k y a h x
0 for
) ( 4 ) ( ) ii (
2
<
=
a
k y a h x
0 for
) ( 4 ) ( ) iii (
2
>
=
a
h x a k y
0 for
) ( 4 ) ( ) iv (
2
<
=
a
h x a k y
Determine the vertex, focus, and directrix
and sketch the graph of the parabola.
Example 25
and sketch the graph of the parabola.
28 8 4
2
= y x x
FHMM1034
Mathematics III
80
Example 26
. 2 curve Sketch the
2
x y =
curve. s Sketch thi vertex. its of
s coordinate the state and parabola a of
equation the is ) 2 ( 2 that Show
2
y x y + =
FHMM1034
Mathematics III
81
Shifted Hyperbolas
FHMM1034
Mathematics III
82
1
) ( ) (
2
2
2
2
=

b
k y
a
h x
1
) ( ) (
2
2
2
2
=

b
h x
a
k y
A shifted conic has the equation
Example 27
=
Complete the square in x and y to show that
the equation represents a hyperbola.
Hence states all its properties and sketch this
graph.
16 32 16 72 9
2 2
= y y x x
FHMM1034
Mathematics III
83
graph.
1.10 1.10
Parametric
Equations
FHMM1034
Mathematics III
84
Equations
Parametric Equations
If f and g are functions defined on an interval I,
then the set of points ( f(t), g(t) ) is a plane

then the set of points ( f(t), g(t) ) is a plane
curve. The equation
) , ( : point moving A y x P
FHMM1034
Mathematics III
85
where t I, are parametric equations for the curve.
) (t f x =
) (t g y =

Parametric Equations
Parametric equation for Ellipse:
t b y sin =
Parametric equation for Parabola:
Parametric equation for Hyperbola:
t a x cos =
t b y sin =
2
at x =
at y 2 =
FHMM1034
Mathematics III
86
t a x sec =
t b y tan =
Example 28
having of equation Cartesian the Find P
. 1 2 and equations parametric
2
+ = = t y t x
FHMM1034
Mathematics III
87
Example 29
locus the of equation cartesian that the Prove
.
1
2 11
is 2
and 3 1 equations parametric with
locus the of equation cartesian that the Prove
3
x
x
y y
t x
t

= + =
=
88
Describe and graph the curve represented by the
parametric equations
Example 30
parametric equations
t x cos =
t y sin = 2 0 t
FHMM1034
Mathematics III
89
(Page 803)
Example 31
parametric with curve the intersects
line the for which of values of range the Find
= x k y
k
of points the find and curve, the o tangent t a is
line the for which of values the State
points. real at , 2 equations
parametric with curve the intersects
2
=
= =
=
x k y k
y t x
x k y
t
90
. 5 when curve
the and line e between th on intersecti
of points the find and curve, the o tangent t a is
=
=
k
x k y
1.11 1.11
Loci
FHMM1034
Mathematics III
91
Loci
its such that curve, a on or line straight a in either
moves, planes coordinate on the ) , ( point a If y x P
. of locus the called is points such of set
the , conditions certain by restricted is movement
its such that curve, a on or line straight a in either
P
the satisfying , and between ip relationsh The y x
FHMM1034
Mathematics III
92
. of locus
the of equation cartesian the called is , conditions
the satisfying , and between ip relationsh The
P
y x
Example 32
A and ) 5 , 4 ( are points two of s coordinate The

BP AP
y x P
B
(i)
such that ) , ( point
a of locus the of equation the .Find ) 1 , 2 (
=

FHMM1034
Mathematics III
93
BP AP
BP AP
2 (ii)
(i)
=
=
The End The End
Of
Chapter 1
FHMM1034
Mathematics III
94
Chapter 1