Additional

Mathematics
Formulae List
Form 5
(prepared by:BEHPC)
1
01 Proressions
Arithmetic Proression !eometric Proression
1" Common #i$$erence
1 n n
d T T

=
%" &he n
th
term
( 1)
n
T a n d = +
'" ()m o$ the $irst n terms
[ ] d n a
n
S
n
) 1 ( 2
2
+ =
or
[ ]
2
n
n
S a l = +
where l = last term
1" Common *atio
1
n
n
T
r
T

=
%" &he n
th
term
1 n
n
T ar

=
'" ()m o$ the $irst n terms
( )
1
, 1 for 1
1
n
n
a r
S r r
r

= >

( )
1
, 1, for 1
1
n
n
a r
S r r
r

= <

+" ()m to in$inity:

1 ,
1
<

r
r
a
S
,$
n
S
is i-en as a $)nction o$ n, then use:
1 n n n
T S S

=
First term, 1 1
a T S = =
Second term, 2 2 1
T S S =
()m o$ the terms $rom m
th
term to n
th
term:)
1
Sum
n m
S S

=
(For example The sum from 3
rd
term to 7
th
term,
7 2
Sum S S =
)
2
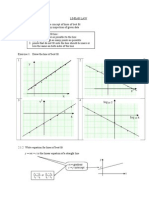
0% .inear .a/
1. Drawing lines of best fit
2. Equations of lines of best fit
3. To reduce non-linear functions
to linear form
set of two !aria"les are related non
linearl# can "e con!erted to a linear
e$uation% The line of "est fit can "e written
in the form
where
X and Y are in terms of x and&or y
m is the 'radient,
c is the Y(intercept
The 'raph of can "e used to find the !alues
of constants of the non(linear e$uation and
others information relatin' the two !aria"les%
)ecall*
(1) E0)ation o$ a straiht line i$ t/o points
are i-en:
(%) E0)ation o$ a straiht line i$ m and c
are i-en:
&ips:
(1) &he e0)ation m)st ha-e one constant
(/itho)t x and y)"
(%) Y cannot ha-e constant1 b)t can ha-e x
and y%
(') X cannot ha-e y%1 b)t can ha-e x and
constant"
3
Line of best fit has 2 characteristics:
it passes throu'h as man# points as possi"le,
the num"er of points which are not on the
line of "est fit are e$uall# distri"uted on the
"oth sides of the line%
Steps to draw a line of best fit:
+onstruct a ta"le consistin' the 'i!en
!aria"les%
,lot a 'raph of Y a'ainst X , usin' the
scale specified -. draw a line of "est
fit%
+alculate the 'radient, m, and 'et the Y-
intercept, c, from the 'raph%
)e(write the ori'inal e$uation 'i!en and
reduce it to linear form%
+ompare with !alues of m and c o"tained,
find the !alues of the un/nowns re$uired%
The ta"le shows some of examples of non(linear e$uations can "e reduced to the linear form*
2on3linear e0)ation .inear e0)ation Y X m c
2
y px qx = +
y
px q
x
= +
y
x
x p q
2
y q
p
x x
= +
2
y
x
1
x
q p
q
y px
x
= +
2
xy px q = + xy
2
x
p q
2
y q
p
x x
= +
y
x
2
1
x
q p
q
y p x
x
= +
y x px q = + y x x p q
y q
p
x x
= +
y
x
1
x
q p
1
p q
y x
= +
1 1 q
y px p
= +
1
y
1
x
q
p
1
p
x
y
p qx
=
+
1 1
p q
y x

= +


1
y
1
x
p q
2
2
0
( ) y x q
p
= +
3 3q
y x
p p

= +


y x
3
p
3q
p
x
y pq =
11 11 11
lo' lo' lo' y x q p = +
11
lo' y
x
11
lo' q
11
lo' p
q
y px =
11 11 11
lo' lo' lo' y q x p = +
11
lo' y
11
lo' x
q
11
lo' p
1 x
y pq
+
=
11 11 11
lo' ( 1)lo' lo' y x q p = + +
11
lo' y
x +1
11
lo' q
11
lo' p
2
0' ,nteration
4. Finding Equation Of A Curve From ts !radient Function:
Gradient function
The equation
of the curve
Differentiati
on
Integration

= dx x f y ) ( 3
4
ntegration is the inverse process of differentiation.
f " then where c # constant.
ndefinite integrals:$)efer to the examples "elow after note 5)
$a%
$&%
$c%
'. (efinite integrals

The laws of definite integrals:
(a)
(")
(c)
(d)
(e)
). ntegration As *he Summation Of Areas:

Area &ounded &+ the curve +#
f$,%"the lines , # a" , # & and the
,-a,is

=
b
a
ydx A
Area of the region between a
curve y = f(x) and a straight line
y = g(x)

=
b
a
b
a
dx x g dx x f A ) ( ) (
5
Area &ounded &+ the curve , # f$+%"
the lines + # a" + # & and the +-a,is.

=
b
a
xdy A
.. ntegration As *he Summation Of /olumes

)efer to -ote 3*

Example
2
4
4
1
2
x
dx x dx c
x

= = +

( )
and ! are functions in
u v dx udx vdx
u x
=

Example
1%
2 2
3 2 3 2 x xdx x dx xdx + = +

3 2
3 2 3
3 2
x x
c = + + =
3
3
x 2
+
2
2
x
3 2
c
x x c
+
= + +
*he volume of the solid generated
when the region enclosed &+ the
curve + # f$,%" the ,-a,is" the line
, # a and the line , # & is revolved
through '.01 a&out the ,-a,is is
given &+

=
b
a
x
dx y !
2

Example

Example
Example
7
Example
2
4
4
2 2 2
( )
3 3 3 2
x
dx x dx c
x

= = +

2
=
2
(
3 2
x

2
)
5
x
c c

+ = +

*he volume of the solid generated

when the region enclosed &+ the
curve , # f$+%" the +-a,is" the line +
# a and the line + # & is revolved
through '.0 1 a&out the +-a,is is
given &+

=
b
a
y
dy x !
2

Example Example
Example
6
0+ 4ectors
0
Vector is a quantit+ that has &oth magnitude and direction.
Scalar is a quantit+ that has magnitude only.
A vector can &e presented &+ a line segment with an arrow" 2nown as a
directed line segment.
egative vector of has the same magnitude as &ut its direction is opposite
to %
A !ero vector ia a vector whose magnitude is 3ero. t is denoted &+ .
*wo vectors are e"ual if &oth the vectors have the same magnitude and
direction.
4hen a vector is multiplied &+ a scalar " the product is . ts magnitude is
times the magnitude of the vector .
*he vector is #arallel to the vector if and onl+ if " where is a constant.
f the vectors and are not parallel and " then and .
Addition of vectors

*riangle 5aw 6arallelogram 5aw
*he su&traction of the vector from the vector is written as . *his operation
can &e considered as the addition of the vector with the negative vector of "
i.e. .
11
Column vector:

A unit vector is a vector whose magnitude is one unit.
*he magnitude of the vector can &e calculated using the 6+thagoras7
*heorem.
(i) *o show is parallel to "
*o show A" 8 and C are collinear"
*o find the ratio of A8 :8C
11
7se
A" # "$ =
uuur uuur
05 &rionometric F)nctions
Positive and Negative Angles
Positi-e anles are an'les measure in an
anticloc5/ise rotate from the positi!e x(axis
a"out the ori'in, %%
2eati-e anles are an'les measured in a
cloc5/ise rotation from the positi!e x(axis a"out
the ori'in %%
Six Trigonometric Functions of Any
Angle
sin
y
r
= cos
x
r
= tan
y
x
=

sin
tan
cos

=

1 cos
cot
tan sin

= =

1
sec
cos

=

1
cosec
sin

=
Complementary Anle
sin cos(01 ) =
cos sin(01 ) =
tan cot(01 ) =
cot tan(01 ) =
sec cosec(01 ) =
cosec sec(01 ) =
2eati-e Anle
sin( ) sin =
cos( ) cos =
tan( ) tan =
Positi-e62eati-e sin at di$$erent 0)adrant
8ust remem"er
the positi!e
ratio999
12
( A
&
C
1
sin x
cos x
cot x tan x
13
sec x
cot x
4al)e o$ (pecial Anle '0
o
and 70
o

1
sin31
2
=

3
cos31
2
=
1
tan31
3
=
3
sin51
2
=
1
cos51
2
= tan51 3 =
4al)e o$ (pecial Anle +5
o

1
sin 24
2
=

1
cos 24
2
=

tan 24 1 =
4al)e o$ (pecial Anle 0
o
1 80
o
1 190
o
1 %:0
o
1 '70
o
"
0
o
80
o
190
o
%:0
o
'70
o
sin
1 1 1 (1 1
0
o
80
o
190
o
%:0
o
'70
o
cos
1 1 (1 1 1

0
o
80
o
190
o
%:0
o
'70
o
tan 1 1 1
Alternati-e ;ay:

0
o
'0
o
+5
o
70
o
80
o
sin
1
2
1
2
2
2
3
2
2
2
1
1
2
2
2
3
2
1
cos
2
2
3
2
2
2
1
2
1
2
1
3
2
2
2
1
2
1
tan 1
1
3
1 3
Steps to solve simple trigonometric equation*
(1) .etermine the rane of !alues of the re$uired
an'les%
(2) Find a basic anle "# usin' calculator%
(3) .etermine the 0)adrants the an'le should "e%
(2) .etermine the -al)es o$ anles in those
$uadrants%
12
Graphs of The Functions of Sine,
Cosine and Tangent
!raph o$" y < sin x
x 0
o
80
o
190
o
%:0
o
'70
o
sin 1 1 1 (1 1
!raph o$" y < cos x
x 0
o
80
o
190
o
%:0
o
'70
o
cos x 1 1 (1 1 1
!raph o$" y < tan x
x 0
o
80
o
190
o
%:0
o
'70
o
tan x 1 1 1
14
Basic Trigonometric Identities:
2 2
sin cos 1 x x + =
2 2
tan 1 sec x x + =
2 2
cot 1 cosec x x + =
Compound AnglesFormulae:
sin( ) sin cos cos sin A " A " A " =
cos( ) cos cos sin sin A " A " A " = m
tan tan
tan( )
1 tan tan
A "
A "
A "

=
m
Double Angle Formulae:
sin 2 2sin cos A A A =
2 2
cos 2 cos sin A A A =
or
2
cos 2 2cos 1 A A =
or
2
cos 2 1 2sin A A =
2
2tan
tan2
1 tan
A
A
A
=

al! Angle Formulae:

sin 2sin cos
2 2
A A
A =
2 2
cos cos sin
2 2
A A
A =
or
2
cos 2cos 1
2
A
A =
or
2
cos 1 2sin
2
A
A =

2
2tan
2
tan
1 tan
2
A
A
A
=

15
For riht anled trianle1 )se:
07 Perm)tations and Combinations
Multiplication Principle / Rule
Permutations
Permutation of n Different Objects,
Taken r at a Time
Combinations
The num"er of perm)tations of n
different o":ects, ta/en r at a time is
'i!en "# *
permutation of n different o":ects,
ta/en r at a time, is an arranement of a
set of r o":ects chosen from n o":ects%
The order of the ob&ect' in the chosen set
is ta/en into consideration%
The num"er of permutations of n
different o":ects, ta/en all at a time, is *
-ote* (i)
(ii)
(iii)
17
;f an operation can "e carried out in r wa#s and
another operation can "e carried out in s
wa#s, then the num"er of wa#s to carr# out
"oth the operations consecuti!el# is r s1 i%e%
rs%
The rs m)ltiplication principle can "e expanded
to three or more operations% ;f the num"ers of
wa#s for the occurrence of e!ents A, " and $
are r, ' and p respecti!el#, the num"er of
wa#s for the occurrence of all the three
e!ents consecuti!el# is r ' p, i%e% rsp%
The n)mber o$ perm)tations of n different
o":ects is n", where
n", is read as n factorial%
The num"er of combinations of r
o":ects chosen from n different
o":ects is 'i!en "# *
combination of r ":ects chosen
from n different o":ects is a selection
of a set of r o":ects chosen from n
o":ects% The order of the o":ects in the
chosen set is not ta/en into
consideration%
-ote* (i)
(ii)
(iii)
(i!)
16
0: Probability
1% The pro"a"ilit# for the occurrence of an e!ent in the sample space S is
num"er of outcomes of e!ent
( ) =
num"er of outcomes of sample space
A
( A
S
( )
( )
( )
n A
( A
n S
=
2% (a) The ran'e of !alues of a pro"a"ilit# is
1 ( ) 1 ( A
%
(") ;f ((A) = 1, e!ent A is sure to occur%
(c) ;f ((A) = 1, e!ent A #ill not occur%
3% The complement of an e!ent is denoted "#
A
and the pro"a"ilit# of a complementar# e!ent is
'i!en "#
2% The pro"a"ilit# for the occurrence of e!ents A or " or "oth is
( ) ( ) ( ) ( ) ( A " ( A ( " ( A " = +
4%
;f the e!ents and < are mutuall# exclusi!e, then A " = and
( ) 1 ( A " =
% Thus,
( ) ( ) ( ) ( A " ( A ( " = +
5% The pro"a"ilit# of the com"ination of two independent e!ents, and <, if the occurrence or non(
occurrence of one e!ent does not affect of the other is 'i!en "#
( ) ( ) ( ) ( A " ( A ( " =
7% The concept of the pro"a"ilit# of two independent e!ents can "e expanded to three or more
independent e!ents% ;f A, " and $ are three independent e!ents, the pro"a"ilit# for the occurrence
of e!ents A, " and $ is
( ) ( ) ( ) ( ) ( A " $ ( A ( " ( $ =
6% tree dia'ram can "e constructed to show all the possi"le outcomes of an experiment%
10
( ) 1 ( ) ( A ( A =
09 Probability #istrib)tions
21
2=*MA. #,(&*,B>&,=2(
+ontinuous random !aria"le is a !aria"le
that can ta/e an# infinite !alue in a
certain ran'e%
normal distri"ution is a pro"a"ilit#
distri"ution of continuous random
!aria"les (onl# $uantities that can "e
measured)%The distri"ution is denoted "#
where = mean and = !ariance%
normal distri"ution with =1 and = 1 is
/nown as a standard normal distri"ution
and is denoted "# ) (1,1)%
normal random !aria"le, X, can "e
con!erted into standard normal random
!aria"le "# usin' %
* = standard score or +(score
X = !alue of a normal random
!aria"le
= mean of a normal
distri"ution
= standard de!iation of a
normal distri"ution
P*=BAB,.,&? #,(&*,B>&,=2(
B,2=M,A. #,(&*,B>&,=2(
1% random !aria"le that has !inite and
countable !alues is /nown as a discrete
random variable%
2% For a <inomial .istri"ution, the pro"a"ilit#
of o"tainin' r num"ers of successes out of
n experiments is 'i!en "#

where
( = pro"a"ilit#
X = discrete random !aria"le
r = num"er of success (1, 1, 2, 3, =,n)
n = num"er of trials
p = pro"a"ilit# of success in an experiment
(1 > p >1)
q = pro"a"ilit# of failure in an experiment
( )
3% "inomial pro"a"ilit# distri"ution can "e
plotted as a grap$%
2% .etermine the mean, !ariance and standard
de!iation of "inomial distri"ution
;f X is a "inomial discrete random !aria"le
such that X?" (n, p), then
@ean of X,
Aariance of X,
Standard de!iation of X,
%ormal Distribution
1% continuous random !aria"le, X, is normall# distri"uted if the 'raph of its pro"a"ilit# function
has the followin' properties%
;ts cur!e has a "ell shape and it is s#mmetrical at the line x = %
;ts cur!e has a maximum !alue at x = %
The area enclosed "# the normal cur!e and the x(axis is 1%
08 Motion Alon a (traiht .ine
9.1 Displacement
1% (a) Positi-e displacement means that the particle is at the ri'ht(hand side of %%
(") 2eati-e displacement means that the particle is at the left(hand side of %%
(c) @ero displacement means that the particle is at %%
2% Total distance tra!elled in the $irst n seconds is the total distance tra!elled "# a particle from time
t = 1 to t = n%
3% #istance tra!elled durin' the nth second is the distance tra!elled "# the particle from time t = (n
1) to t = n%
Thus, #istance tra!elled durin' the nth second <
1 n n
S S

9.2 Velocity
1% ;nstantaneous !elocit#, v, is the rate of chan'e of displacement, ', with respect to time, t and it is
'i!en "#
d'
v
dt
=
2% (a) Bhen a particle mo!es to the riht, it has a positi-e -elocity%
(") Bhen a particle mo!es to the le$t, it has a neati-e -elocity%
(c) Bhen a particle is instantaneo)sly at rest, it has a Aero -elocity%
3% The displacement of particle is a maBim)m (to the ri'ht or to the left of the fixed point %) when
its -elocity is Aero%
21
2% particle re-erses its direction when it comes to instantaneous rest, i%e% v < 0%
4% .isplacement, ', is 'i!en "# the inte'ration of the instantaneo)s -elocity, !, with respect to time,
t, i%e%


5% #istance tra!elled durin' the nth second <
1
n
n
vdt

7% The displacement of particle is a maBim)m (to the ri'ht or to the left of the fixed point %) when
its -elocity is Aero%
6% particle re-erses its direction when it comes to instantaneous rest, i%e% v < 0%
9.3 Acceleration
1% cceleration is the rate of chan'e of !elocit#%
2
2
dv d '
a
dt dt
= =
v a dt =

2% (a) Positi-e acceleration means that the -elocity is increasin with respect to time%
(") 2eati-e acceleration or deceleration means that the -elocity is decreasin with respect to
time%
(c) @ero acceleration means that the -elocity is a constant ()ni$orm -elocity)%
3% The -elocity of a particle is a maBim)m when its acceleration is Aero%
2% The followin' conclusion can "e made%
22
v
s
d'
v
dt
=
' v dt =

a
dv
a
dt
=
2
2
d '
a
dt
=
v a dt =

23
Important tips:
;nitial displacement & initial !elocit# & initial acceleration
(a) at the ri'ht(hand side of %
(") 2 m to the ri'ht of %
(a) at the left(hand side of %
(") 2 m to the left of %
when the particle mo!es to the ri'ht
when the particle mo!es to the left
when the particle is instantaneousl# at rest
when particle re!erses its direction
when the particle returns to %
maximum displacement of the particle or
maximum !elocit# of the particle or
!elocit# is increasin' & positi!e acceleration
!elocit# is decreasin' & ne'ati!e acceleration
uniform !elocit#(!elocit# is a constant) & Cero acceleration
when particle , and particle ) meet
22
10 .inear Prorammin
1% Dinear pro'rammin' is a method of sol!in' pro"lems in!ol!in' two !aria"les that can "e
represented "# a mathematical model "# usin' ine$ualities as constraints%
2%
3% 8ust remem"er how to shade the re'ions which are 'reater than*
(a)
1 y (") 1 x
(c)
y b
(b = y(intercept)
(d) x a (a = x(intercept)
24
For or , use solid line ()%
For E or > , use dashed line ((((()%
x
%
y
x
%
y
x
%
y
y b =
x
%
y
x a =
a
b
(e)
y mx c +
(m = positi!e !alue) (f)
y mx c +
(m = ne'ati!e !alue)
(F'*
2 1 y x +
) (F'*
2 1 y x +
)

2% constraint is an inequality that represents a condition that must "e satisfied in order for a
pro"lem to "e sol!ed%
Constraint &nequality
1% y is more than x
y x >
2% y is less than x
y x <
3% y is not more than x
y x
2% y is not less than x
y x
4% y is at least # times of x
y #x
5% y is at most # times of x
y #x
7%
The total x and y is not more than
#
x y # +
6% The smallest !alue of y is #
y #
0% The 'reatest !alue of y is #
y #
11% x exceeds two times of y at least #
2 x y #
11% The ratio of y to x is # or more
y
#
x

4% ;mportant /e#words*
not less than
at least
smallest !alue
minimum !alue
25
x
%
y
x
%
y
y mx c = +
y mx c = +

5% Steps to sol!e a linear pro'rammin' pro"lem throu'h 'raphical method*
Step 1* .etermine the two !aria"les, x and y%
Step 2* From the 'i!en constraints, interpret the pro"lem and form ine$ualities that satisf# all
the constraints%
Step 3* .raw the strai'ht lines for each ine$ualit#%
Step 2* .etermine the re'ion which satisfies all the ine$ualities%
Step 4* Form the optimal function
# ax by = +
%
Step 5* <# usin' a ruler and set s$uare, slide the line towards the re'ion to find the maximum
or minimum point "ased the function%
Step 7* .etermine the optimal !alue (maximum or minimum !alue)%
*O 9: 8E5O/E( S*;(E<*S===
>!OO( 5;C? @ A55 *AE 8ES* >
< :O;B S69 ECA9<A*O<
4SA<! :O; *AE /EB: 8ES* < E/EB:*A<! A<( 9A: A55 *AE <CES*
*A<!S :O; 4SA FOB A54A:S CO9E *O :O;.
8ES* 4SAES"
6< 8EA
not more than
at most
'reatest !alue
maximum !alue
27

26