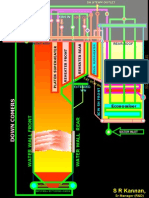
Documente Academic
Documente Profesional
Documente Cultură
Control System Theory
Încărcat de
Nishant SaxenaDrepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
Control System Theory
Încărcat de
Nishant SaxenaDrepturi de autor:
Formate disponibile
1
CONTROL SYSTEM THEORY
1. INTRODUCTION
2. Transfer Function
3. Block Diagram
4. Time Response Analysis of Control System
5. Error analysis
6. Stability analysis of Control System
7. Root Locus
8. Nyquist Stability
9. Bode Plots
10. Laplace Transform
11. State Variables
12. Practice Set
2
Comparat or
Control
Action
error
e Input
r
cc
Output
Measuring
Element
1. INTRODUCTION
Open Loop Control System
Control
Input Output
Action
In a open loop Control System the output is neither measured nor feedback for comparison with input.
Faithfulness of an open loop control system depends on the accuracy of input calibration
Closed-Loop Control System
In a closed loop control system the output has an effect on control action through a feedback as shown fig.
and hence closed loop control systems one also termed as feedback control systems. The control action is
actuated by an error signal which is the difference b/w the input signal r and the output signal c, this
process of comparison b/w the output and input maintains the output at a desired level through control action
process
Open Loop Systems Closed Loop
1. Automatic coffee server 1. Electric Iron
2. Traffic Signal 2. D.C motor speed control
ADVANTAGES
3. Simple and economic 3. Accurate and reliable
Disadvantages
4. Unreliable 4. The system is complex and costly
5. Inaccurate 5. System may become unstable
2. Transfer Function
( ) ( ) ( )
( )
( )
( )
Input response
or Function or output
Transfer
Function
R s G s C s
C s
G s
R s
=
( ) ( ) ( )
( )
( )
( )
Input response
or Function or output
Transfer
R s G s C s
Function
C s
G s
R s
=
Poles and Zeros of Transfer Function
1
0 1
1
0 1
( )
( )
( )
n n
n
m m
n
a S a S a A s
G s
B s b S b S b
+ + +
= =
+ + +
3
A AB AB+C
C
B
+
+
+
A A+C
C
B
+
+
+
A
AB+C
B
+
+
C
A AB
C
C
+
+
AB+C
+
G
1
G
2
AG
1
AGG
1 2 A
G
2
G
1
Ag
2
AGG
1 2 A
G
1
G
2
AG
1
AGG
1 2 A
GG
1 2
AGG
1 2 A
G
1
AG +AG
1 2 A
+
+
G
2
AG
1
AG
2
G+G
1 2
A
AG+AG
1 2
1 2 3 0
0
( )( )( ) ( ) ( )
( )
( ) ( )( ) ( )
b m
K S S S S S S S S A s
G s
B s S S S S S S
= =
Where
0
0
a
K
b
= is known as the gain factor of the transfer function
Poles of the transfer function In the transfer function expression if S is put equal to S
a
, S
b
, ---- S
m
It
is noted that the value of the transfer function is infinite. Hence S
a
, S
b
, ------ S
m
are called the poles of the
transfer function.
Zeros of the transfer function In the transfer function expression if S is put equal to S
1
S
2
S
3
---- S
n
It
is noted that the value of the transfer function is zero Hence S
1
S
2
S
3
-------- S
n
are called the zeros of the
transfer function
Q.1.
( 2)( 4)
( )
( 3)( 5)( 2 4 )( 2 4 )
s s
G s
s s s s j s j
+ +
=
+ + + + +
Solution Poles are at
s = 0, s = 3, s = 5, s = 2 + 4j, s = 2 4j
As the number of zeros should be equal to number of polar, the remaining three zeros are located
at s =
3. BLOCK DIAGRAM REDUCTION
ORIGINAL BLOCK EQUIVALENT BLOCK
DIAGRAMS
(1)
(2)
(3)
(4)
(5)
4
G
AGB
A
+
AG
B
G
AGB A
+
1/G
B
A
B
G
G
AGB A
+
AB
B
G
AGBG
A
+
G
AG
BG
B
G
A
AG
AG
G AG
G AG
A
G
A
AG
A
G AG
G AG
A
AG
G
1
A
+
G
2
B
G
1+G G
1
1 2
B A
G
1
+
C(s) R(s)
+
G
2
H
1
H
3
H
2
G
1+G H
1
1 1
R(s)
+
G
1+G H
2
2 2
H
3
C(s)
G G
(1+G H )(1+G H )
1 2
1 1 2 2
R(s)
+
H
3
C(s)
1
R
1
V (s)
1
+
V (s)
0
+
1
SC
1
+
1/R
2
1
SC
2
1
R
1
R(s)
+
C(s) +
1
SC
1
+
1/R
2
1
SC
2
SC
2
(6)
(7)
(8)
(9)
(10)
Q.1. Drive the transfer function using block reduction technique
Solution :
2 2
1 1 2 2 1 2 3 1 2 1 2
( )
( ) 1
G G C s
R s G H G H GG H GG H H
=
+ + + +
Q.2.
Solution :
5
1
R
1
R(s)
+
C(s) +
1
SC
1
+
1/R
2
1
SC
2
SC
2
1
R
1
R(s)
+
C(s) +
1
SC
1
1
1+R SC
2 2
SC
2
1
R
1
R(s)
+
C(s) +
1
SC
1
1
1+R C S
2 2
SC
2
1+R C S
2 2
1
R
1
R(s) +
C(s)
1
SC +R C C S +SC
1 1 1 2 2
2
1+R C S
2 2
R(s) +
C(s)
1
R C S+R C C S +SC
1 1 1 1 2 2
2
1+R C S
2 2
R(s)
+
C(s)
+
G
1
G
2
G
3
H
2
H
1
R(s)
+
C(s)
+
G
1
G
2
G
3
H
2
H
G
1
3
+
2
1 2 1 2 1 1 2 2 1 2
( ) 1
( ) ( ) 1
C s
R s S R R CC RC R C RC S
=
+ + + +
Q.3. Find
( )
( )
C s
R s
6
R(s)
+
C(s)
+
G
1
G G
1+G H G
2 3
2 2 3
H
G
1
3
R(s)
C(s)
G G G
1+G G H G H G
1 2 3
2 3 2 1 1 2
+
R(s)
C(s)
+
G
H
2
H
2
+
R(s)
C(s) G
H
2
H
G
2
+
+
G
1+GH
2
H
G
1
1+
R(s)
C(s)
G+H
1+GH
1
2
R(s)
C(s)
R(s)
+
C(s) +
+
G
3
H
2
G
1
H
1
G
2
R(s)
+
C(s)
+
G
3
H
G
2
3
G
1
H
1
G
2
R(s)
+
C(s)
+
G
1+G H
3
3 1
H/G
3
G
1
G
2
R(s) +
C(s) G
1
G G
1+G H G H
2 3
3 1 2 2
1 2 3
2 3 2 1 2 1 1 2 3
( )
( ) 1
GG G C s
R s G G H GG H GG G
=
+ + +
Q.4. Find
( )
( )
C s
R s
Solution :
1
2
( )
( ) 1
G H C s
R s GH
+
=
+
Q.5. Find the ratio
Solution :
7
R(s) C(s)
1/S 3
1
+
1/S
3
2
+
+
+
1/S 3
3
+
+
+
C(s)
1
S+2
6
+
+
+
1
S+1
3
1
S+3
3
R(s)
C(s)
6
S+2
+
+
+
3
S+1
3
S+3
R(s)
R
1
G
1
H
1
H
2
G
2
G
3
G
4
G
5
H
3
H
4
S
1 2 3
3 1 2 2 1 2 3
( )
( ) 1
GG G C s
R s G H G H GG G
=
+ + +
Q.6.
Solution :
3 2
( ) 3 6 3 ( ) 6
( ) 1 2 3 ( ) 6 11 6
C s C s
R s s s s R s s s s
= + =
+ + + + + +
4. MASONS GAIN FORMULA FOR SIGNAL FLOW GRAPH
1
k n
k k
k
P
P
=
=
A
=
A
Where P
k
= path gain or transmittance of Kth forward path
, , ,
1
b c d e f
a b c d e f
La L L L L L A = + +
a
a
L
= sum of all individual loop gains
,
b c
b c
L L
= sum of gain products of all possible combinations of two nontouching loops
, ,
d e f
d e f
L L L
= sum of gain products of all possible combinations of three non touching loops
Q.1. Find the ratio
C
R
8
C
+
+
+
G
6
G
3
G
2
G
1
+ +
G
5
G
4
H
1
H
2
R
R
G
1
H
1
H
2
G
2
G
3
G
6
G
4
H
2
C
G
5
+
+
G
3
G
2
G
1
+
G
4
R
C
R
G
1
1
G
2
G
3
1
1
G
4
C
1
Solution : g
1
= G
1
G
2
G
3
G
4
g
2
= G
1
G
5
L
1
= G
1
H
1
L
2
= G
3
H
2
L
3
= G
1
G
2
G
3
H
3
L
4
= H
4
Two non-touching loop
L
1
L
2
= G
1
G
3
H
1
H
2
L
1
L
4
= G
1
H
1
H
4
L
2
L
4
= G
3
H
2
H
4
L
3
L
4
= G
1
G
2
G
3
H
3
H
4
Three - non touching loops
L
1
L
2
L
4
= G
1
H
1
G
3
H
2
H
4
A
1
= 1 0 A
2
= 1 + G
3
H
2
A = 1 (L
1
+ L
2
+ L
3
+ L
4
) + (L
1
L
2
+ L
1
L
4
+ L
2
L
4
+ L
3
L
4
) (L
1
L
2
L
4
)
1 1 2 2
1 2 3 4 1 5 3 2
1 1 3 2 1 2 3 3 4 1 3 1 2 1 1 4 3 2 4 1 2 3 3 4 1 3 1 2 4
(1 )
1
g g C
R
GG G G GG G H C
R G H G H GG G H H GG H H G H H G H H GG G H H GG H H H
A + A
=
A
+ +
=
+ + + + + + + + +
Q.2. Find
C
R
Solution :
1 1 2 4 2 1 2 3 6 3 1 2 5 6 c
g GG G G g GG G G g GG G G = = =
L1 = G1H1 L2 = G1G2G3H2 L3 = G1G2G4H2
L4 = G1G2G5H2
1 2 3 4
1 1 1 2 3 2 1 2 4 2 1 2 5 2
1 1 2 2
1 2 3 6 1 2 4 6 1 2 5 6
1 1 1 2 3 2 1 2 2 4 1 2 5 2
1 ( )
1
1
L L L L
G H GG G H GG G H GG G H
g g C
R
GG G G GG G G GG G G C
R G H GG G H GG H G GG G H
A = + + +
A = + + + +
A + A
=
A
+ +
=
+ + + +
Q.3.
Find
C
R
Solution :
9
R
+
C
+
G
1
G
2
G
3
G
4
H
1
H
2
+
+
R
G
1
H
1
G
2
G
3
1
C
1
H
2
G
4
+
+
G
3
G
2
G
1
+
+
G
4
R
C
H
1
H
2
+
1 1 2 3 2 4
1 2 1 2 2 3
1 1 2 2 2 3
1 1 2 2
1 2 3 4 1 2 2 3
1 2 2 3
1 1
(1 )
1
g GG G g G
GG G G
L GG L G G
g g C
R
GG G G GG G G C
R GG G G
= =
A = A = +
= =
A + A
=
A
+ +
=
+
Q.4. Find
C
R
Solution :
1 1 2 3 1
2 1 4 2
1 1 2 1 2 2 3 2 3 1 2 3
4 1 4 5 4 2
, 1
1
g GG G
g GG
L GG H L G G H L GG G
L GG L G H
= A =
= A =
= = =
= =
1 1 2 2
g g C
R
A + A
=
A
Q.5.
Solution : g
1
= G
1
G
2
G
3
g
2
= G
4
L
1
= G
2
H
1
L
2
= G
2
G
3
H
2
L
3
= G
1
G
2
H
1
1 2 2 1 1 2 1 2 3 2
2 1 1 2 1 2 3 2
1 2 3
1 2 3 4 2 1 1 2 1 2 3 2
2 1 1 2 1 2 2 3
1 1 ( )
1
1 ( )
(1 )
1
G H GG H G G H
G H GG H G G H
L L L
GG G G G H GG H G G H C
R G H GG H G H G
A = A =
= + + +
A = + +
+ + + +
=
+ + +
10
r(t)=1
t
steady
state error
transient
steady
state
C(t)
r(t)
t
A
t
r(t)
t
r(t)
R(s)
C(s)
1
ST
+
C(s)
1
ST+1
R(s)
4. TIME RESPONSE ANALYSIS OF CONTROL SYSTEM
TRANSIENT AND STEADY STATE RESPONSE
The time response of a control system is divided in two
Parts namely
(i) Transient response
(ii) Steady State Response
(i) STEP FUNCTION Step function is described as sudden application of input signal
r(t) = All(t)
u(t) = 1 t > 0
0 t < 0
AL(1) =
A
s
(ii) RAMP FUNCTION The ramp is a signal which starts at a value of zero and increases linearly with
time
r(t) = At t > 0
0 t < 0
In the Laplace transform form
2
( )
A
r t
s
Z =
(iii) PARABOLIC FUNCTION
2
3
( ) 0
2
0 0
( )
At
r t t
t
A
R s
s
= >
<
=
(iv) IMPULSE SIGNAL A unit impulse is defined as a signal which has zero value every where except
at t = 0 where its magnitude is infinite
( ) 0 0
( ) 1
t t
t dt
o
o
o
o
= =
=
}
TIME RESPONSE OF A FIRST ORDER SYSTEM
11
r
(
t)
=
t
T
error
1
T
e
t/T
1
T
C(t)
4T
t
0
1
.632
C(t)=1e
t/T
.98
4T T
.02
C(t)
Slope =
1
T
Transient Steady state
T >T
2 1
0.632
T
1
T
2
4T
1
4T
2
.98
.98
C(t)
1
1
( ) ( ) 1
1
( ) ( ) 1
1
( ) 1 ( ) ( ) 1
1
G s H s
ST
C s G s
ST
R s G s H s ST
ST
= =
= = =
+ +
+
Response of the first order system with unit step input
( ) 1 1 1
( )
( ) 1 1
C s
C s
R s ST ST S
= =
+ +
1 1 1
( ) ( )
1
( 1)
C s C s
S ST S
S
T
= =
+
+
Inverse Laplace
/
( ) 1
t T
C t e
=
The error is given by
/ /
( ) ( ) ( )
1 (1 )
t T t T
t r t e t
e e
=
= =
STEADY STATE ERROR
/
lim 0
t T
t
e
= =
RESPONSE OF THE FIRST ORDER SYSTEM WITH UNIT RAMP FUNCTION
2 2
2
2 2
1 1 1
( ) ( )
1
1 1 1
( ) ( ) .
1
1
R s C s
S ST S
ST T T
C s C s T
S ST S S
S
T
= =
+
= + = +
+
+
Inverse Laplace equation
/
/ /
( ) ( ) ( ) ( )
( ) (1 )
t T
t T t T
C t t T Te e t r t C t
t t T Te e t T e
= + =
( = + =
Steady State error
/
lim( )
t T
t
T Te T
= =
Response of the first order system with unit impulse function
1
( ) ( )
1
1
( )
1
C s R s
sT
C s
ST
=
+
=
+
12
R(s)
C(s)
+
C(t)
t
Inverse Laplace
1 1 /
1 1 1
( ) ( )
1
t T
L C s L C t e
T T
S
T
= =
+
TIME RESPONSE OF SECOND ORDER SYSTEM
2
2
2 2 2
( ) ( )
( ) 1 ( ) ( )
( 2 ) ( ) ( )
( ) ( ) 2
1
( 2 )
n
n n
n n n
n
C s G s
R s G s H s
s s C s C s
R s R s s s
s s
e
e e
e e e
e
=
+
+
= =
+ +
+
+
TIME RESPONSE OF SECOND ORDER SYSTEM WITH UNIT STEP INPUT
2
2 2
( ) ( )
2
n
n n
C s R s
s s
e
e e
=
+ +
For unit step input
1
( ) R s
s
=
{ }
2 2
2 2 2 2 2
2 2 2 2
2
1
( ) ( )
( 2 2 ) ( ) (1 )
(1 ) 1
1
( ) 1 sin( ) tan
n
n n
n n n n
d n d n
t
d
C s C s
s s s s
C t e t
e
e e
e e e e
e e e e
e | |
= =
+ + + +
= =
= + =
Error signal for the system
e(t) = r(t) c(t)
( )
2
2 1
2
1
( ) sin 1 tan
1
n
t
n
e
e t t
e
= +
`
)
The steady state value of C(t)
lim ( ) 1
ss
t
e C t
= =
e
n
= natural frequency of oscillation or undamped natural frequency
e
d
= damped frequency of oscillation
e
n
= damping factor or actual damping or damping coefficient
(a) Underdamped case (0 < < 1)
(b) When = 0 undamped case
( ) 1 sin
2
( ) 1 cos
n
n
C t t
C t t
t
e
e
= +
`
)
=
(c) = 1 critically damped case
13
98%
C(t)
1
4T
2%
C(t)
2
2
1
( )
( )
n
n
C s
s s
e
e
=
+
2
2 2
2
1 1 1 1
2
( ) ( )
1 1
( )
( )
1 1
( )
( )
( ) 1
( ) 1 (1 )
n n
n
n
n n n
n
n
n n
n
n n
t t
n
t
n
A B C
s s s s s
S
C s
s s s
L C s L L L
s s s
C t e t e
C t e t
e e
e
e
e e e
e
e
e e
e
e e
e
e
= + +
+ + +
=
=
+ +
=
+ +
=
= +
Actual damping
Critical damping
n
n
e
e
= =
(d) > 1 Over damped case
( )
( )
2
2
2 2 2
1
2
2 2
2 2
1
( )
( ) ( 1)
1
( ) ( ) 1
( )
2 1 1
n
n
n n
t
n
n d
C s
s s
e
C s C t
s s
e
e
e e
e
e e
=
+
= =
+
time constant
( )
2
1
1
c
n
t
e
=
Transient Response Specifications of Second Order System
14
1. DELAY TIME (t
d
) The delay time is the time required for the response to reach 50% of the final
value in first time
2. RISE TIME (t
r
) It is the time required for the response to rise from 100% to 90% of its final value
for over damped systems and 0 to 100% for underdamped systems
3. Peak Time (t
e
) The peak time is the time required for the response to reach the first peak of the
time response or first peak overshoot
4. Maximum Overshoot (m
p
) It is the normalized difference between the peak of time response and
steady output the maximum percent overshoot is defined by.
Maximum percent over shoot
( ) ( )
100
( )
p
C t C
C
=
5. SETTLING TIME (t
s
) The settling time is the time required for the response to reach and stay
within the specified range (2% to 5%) of its final value
6. STEADY STATE ERROR (e
ss
) It is the difference b/w actual output and desired output as time t
tends to infinity
| | lim ( ) ( )
ss
t
r t C t
=
Rise time (t
r
)
( )
2
2
( ) 1 sin 1
1
n
t
n
e
C t s t
e
e |
= +
Let response reaches 100% of desired value put C(t) = 1
{ }
2
2
1 1 sin 1
1
n
t
n
e
t
e
e |
= +
( )
2
2
1
2 2
1
1
tan
1 1
n r
r r r
d
n n
t
t t t
e | t
t
t | t |
e
e e
+ =
= = =
Peak time t
p
2
1
p
d
n
n n
t
t t
e
e
= =
First minimum (undershoot) occurs at n = 2
min
2
2
1
n
t
t
e
=
Maximum overshoot : M
p
2
2
2
/ 1
1
max
2
1
max
( ) 1 sin ( ) 1
1
( ) 1 % 100
p p
e
C t C t e
M C t M e
t
t
= + = +
= =
Settling time t
s
4
s
n
t
e
=
15
16
s(s+.8)
R(s) +
1+as
B
R(s)
+
C(s)
+
1
s
16
s+.8
K
Q.1. When a second order control system is subjected to a unit step input the values of = .5 and e
n
6 r/se
determine the rise time, peak times settling time and peak overshoot
Solution
= .5 6 / sec
n
rad e =
(i) Rise time
r
d
t
t |
e
=
2
2
1
2 2
1
1 .5
tan
tan
.25
.403sec
1 6 1 .5
r r r
n
t t t
t
t
= = =
(ii) Peak time
2 2
.605sec
1 6 1 .5
p
n
t
t t
e
= = =
(iii) SETTLING Time
4 4
1.33sec
.5 6
s s
n
t t
e
= = =
(iv) Maximum Overshoot
2
2
.5
1
1 .5
100 100 16.3%
p p
M e e M
t
t
= = =
Q.2. Determine the value of a such that the damping ratio is .5 also obtain the value of rise time and
maximum overshoot M
p
in its step response
Solution
2
16
( ) 16 5(5 .8)
1 16(1 05)
( ) 5 (.8 16 )5 16
5(5 .8)
C s
P s a
+
= =
+ +
+ + +
+
Characteristic equation
2
2 2
5 (.8 16 )5 16 0
5 2 5 0
n n
a
e e
+ + + =
+ + =
2
16, 4 / sec
2 .8 16 2 .5 4 .8 16 .2
n n
n
r
a a a
e e
e
= =
= + = + =
Rise time
2
2
1
1
2 2
1
1 .5
tan
tan
.5
.605sec
1 4 1 .5
r r
n
t t
t
t
= = =
Maximum overshoot
2
.5
1
1 .5
100 100 16.31%
p p p
M e M e M
t t
2
= = =
Q.3. Determine the value of K such that the damping ratio is .5 then obtain the rise time (t
r
), t
p
M
p
and t
s
in the unit step response
16
K
P
R(s) +
H(s)
G(s) C(s)
E(s) E (s)
a
B(s)
R(s)
+
C(s) 1
ST
d
Solution
2
( ) 16
( ) 5 (.8 16 )5 16
C s
R s K
=
+ + +
2
2
2
2
1
1
2 2
2 2
.5
1
1 .5
4 2 .8 16 .2
1
1 .5
tan
tan
.5
1 4 1 .5
.605sec
.906sec
1 4 1 .5
100 100 16.3%
n n
r r
n
r
p
n
p p
K K
t t
t
t
M e e M
t
t
e e
t
t
e
t t
e
= = + =
= =
=
= = =
= = =
Settling time
4 4
( ) 2sec
.5 4
s
n
t
e
= = =
PROPORTIONAL CONTROL
E(s) = R(s) B(s)
R(s) = reference Input E(s) = Error signal E
a
(s) = Actuating signal
C(s) = Output of the system B(s) = Feedback signal
( )
( )
a
p
E s
K
E s
=
Derivative control Actuating signal consists of proportional error signal and derivative of the error
signal
| |
( )
( ) ( ) ( ) ( ) 1
a d a d
de t
e t e t T E s E s ST
dt
= + = +
17
R(s)
C(s)
SK
t
E(s) E (s)
a
R(s)
+
C(s) 1
K
s
i
E (s)
a
E(s)
+
+
( )
2
2
2 2 2 2
2 2 2 2 1 2
1 2 1
(1 5 )
5(5 2 ) (1 5 ) ( ) ( )
( ) ( ) 5 (2 )5
1 (1 5 )
5(5 2 )
5 2 5 0 5 2 5 0
2 2
2
n
d
n n d
n n d n n
d
n
n n d n n n
n d
n n n d
T
T C s C s
R s R s T
T
T
T
T
e
e e
e e e e
e
e e e e e
e
e e e
+
`
+ +
)
= =
+ + +
+ +
`
+
)
+ + + = + + =
= + = +
2
2
2 2 2 2 2
( ) 1
( ) (1 5 )
( ) 1 ( ) ( ) 5(5 2 )
( ) 1
( )
(1 5 ) ( )
1
5(5 2 )
5(5 2 ) 5(5 2 ) ( ) 1
( )
( ) 5(5 2 ) (1 5 ) 5 5 (2 )5
n
d
n
n d
n
n n
n n d n n d n
E s
G s T
R s G s H s
E s
H s
T R s
E s
E s
R s T T
e
e
e
e
e e
e e e e e
= = +
+ +
=
+
+
+
+ +
= =
`
+ + + + + +
)
The steady state error for unit ramp input
0
2 2 2 2
0
2
lim ( )
( 2 ) 1
lim
(2 )
2
2
ss
s
n
s
n n d n
n
ss
n
ss
n
e sE s
s s
s
s s T s
e
e
e
e e e
e
e
=
+
=
+ + +
=
=
Derivative Feedback Control
2
1
2 2 2
( )
( ) (2 ) 2
n n t
n n n
k C s
R s s K s
e e
e e e
= = +
+ + +
2
2 2
2 2
2 2 2 2
2 2
2 2 2 2
( ) 1 1
( ) ( ) ( ) 1
1
(2 )
(2 ) ( ) 1
( )
( ) (2 )
(2 ) 1 2
( )
(2 )
n
n n t
n n t
n n t n
n n t
ss t
n n t n n
E s
R s G s H s
s k s
s k s E s
R s
R s s k s s
s k s
E s e k
s s k s
e
e e
e e
e e e
e e
e e e e
= =
+
+
+ +
+ +
= =
+ + +
+ +
= = +
+ + +
Integral Control
18
R(s)
C(s)
E (s)
a
E(s)
1+ST +
d
K
s
i
G(s)
R(s) +
H(s)
B
E(s)
2
2
3 2 2 2 2
1
( 2 ) ( ) ( ) ( )
( ) ( ) 2
1 1
( 2 )
i n
n i n
n n i n i n
n
k
s s s s k C s C s
R s R s s s s k k
s s s
e
e e
e e e e
e
| |
+
`
|
+ + \ .
)
= =
+ + +
| |
+ +
`
|
+
\ .
)
( ) 1
( ) 1 ( ) ( )
E s
R s G s H s
=
+
2
2
1
( )
1
( 2 )
i n
n
s k
s s
e
e
=
+
+
+
2
3 2 2 2
( 2 )
( ) ( )
2
n
n n i n
s s
E s R s
s s s k
e
e e e
+
=
+ + +
In the input is parabolic input i.e
3
1
( ) R s
s
= then we have steady state error.
2
3 3 2 2 2
2
0
( 2 ) 1
( )
2
2 2
lim ( )
n
n n i n
n
ss ss
s
i n i n
s s
E s
s s s s k
e SE s e
k k
e
e e e
e
e e
+
=
+ + +
= = =
PROPORTIONAL PLUS DERIVATIVE PLUS INTEGRAL CONTROL (PID)
( ) ( ) ( ) ( )
( ) ( ) 1
i
a d
i
a d
K
E s E s ST E s E s
s
K
E s E s ST
s
= +
= + +
`
)
5. ERROR ANALYSIS STEADY STATE ERROR
( ) 1
( ) 1 ( ) ( )
E s
R s G s H s
=
+
steady state error of system is obtained by applying final value theorem
19
0
0
lim ( ) lim ( )
( )
lim
1 ( ) ( )
ss
t s
ss
s
e e t sE s
R s
e s
G s H s
= =
=
+
Unity feedback system H(s) = 1
0
( )
lim
1 ( )
ss
s
R s
e s
G s
=
+
STATIC ERROR COEFEIENTS
(a) Static Position Error Constant K
P
0
( )
lim
1 ( ) ( )
ss
s
s R s
e
G s H s
=
+
For unit step input
1
( ) R s
s
=
0
1 1
lim
1 ( ) ( ) 1
ss ss
s
p
e e
G s H s K
= =
+ +
K
p
= static position error constant
0
lim ( ) ( )
s
G s H s
=
(b) Static Velocity Error Constant K
v
0
1
lim ( )
1 ( ) ( )
ss
s
e SR s
G s H s
=
+
Steady state error with a unit ramp input is given by
2
1
( ) R s
s
=
{ }
2
0 0
0
1 1
lim lim
1 ( ) ( ) ( ) ( )
1
lim ( ) ( )
ss
s s
ss v
s
v
e s
s G s H s s G s H s
e K sG s H s
K
= =
+
= =
Static velocity error coefficient
(c) Static Acceleration error Constant K
a
The steady state error of the system with unit parabolic input is given by
3
1
( ) R s
s
=
3 2
0 0
2
0
1 1 1 1
lim lim
1 ( ) ( ) ( ) ( )
lim ( ) ( )
StaticAccelerationconttant
ss ss
s s
a
a
s
e s e
s G s H s s G s H s K
K s G s H s
= = =
+
=
=
STEADY STATE ERROR FOR DIFFERENT TYPE OF SYSTEMS
(1) Type zero system with unit step input
1
( ) R s
s
=
1 2
0
(1 )(1 )
( ) ( )
(1 )(1 )
lim ( ) ( )
1
1
s b
p p
s
ss
K ST ST
G s H s
ST ST
K G s H s K K
e
K
+ +
=
+ +
= =
=
+
Hence for type zero system the static position error constant K
p
is finite
20
20
s(1+.05s)
R(s)
+
C(s)
E (s)
a
20
1+.01s
1+.05s
B(s)
(b) Type 0 system with unit ramp input
0
lim ( ) ( )
1
v
s
ss
v
K s G s H s
e
K
=
= =
(c) Type 0 system with unit parabolic input
2
0
lim ( ) ( )
1
0
0
a
s
a ss
K s G s H s
K e
=
= = =
For type 0 system, the steady state error is infinite for ramp and parabolic inputs hence the ramp
and parabolic inputs are not acceptable
Q.1. For a unity feedback control system the forward path transfer function is given by
2
20
( )
( 2)( 2 20)
G s
s s s s
=
+ + +
determine the steady state error of the system when the inputs are (i) s (ii) 5t (iii)
2
3
2
t
Solution : (i) r(t) = 5
0 0
0
2
2
2
0
( )
lim ( ) lim
1 ( ) ( )
5
lim
20
1
( 2)( 2 20)
5 ( 2)( 2 20)
lim 0
( 2)( 2 20) 20
ss
s s
s
ss
s
R s
e SE s s
G s H s
s
s
s s s s
s s s s
e
s s s s
= =
+
=
+
+ + +
+ + +
= =
+ + + +
(ii)
2
5
( ) R s
s
=
2
0
2
5 1
lim 10
20
1
( 2)( 2 20)
ss ss
s
e s e
s
s s s s
= =
+
+ + +
(iii)
3
3
( ) R s
s
=
2
3 2
0
3 ( 2)( 2 20)
lim
( 2)( 2 20) 20
ss
s
s s s s
e s
s s s s s
+ + +
=
+ + +
e
ss
=
Q.2. Determine the actuating signal E
a
(s). Also determine the position error constant for unit step input.
Solution : E
a
(s) = 20R(s) B(s)
21
2 2
2
20 ( ) 1 .01
( ) ( ) ( )
(1 .0.5 ) 1 .05
20(1 .01 ) ( ) 20(1 .01 )
( ) ( ) ( ) 20 ( )
(1 .05 ) (1 .05 )
20 ( )
( )
20(1 .01 )
1
(1 .05 )
a
a
a a
a
E s s
C s B s e s
s s s
s E s s
B s E s E s R s
s s s s
R s
E s
s
s s
+
= =
+ +
+ +
= =
+ +
=
+
+
+
Step input
1
( ) R s
s
=
{ }
2
2
2
2
0 0
20(1 .05 )
( )
(1 .05 ) 20(1 .01 )
20(1 .05 )
lim ( ) lim 0
(1 .05 ) 20(1 .01 )
a
ss ss
s s
s
E s
s s s
s s
e sE s e
s s s
+
=
+ + +
+
= = =
+ + +
1
0 ,
1
p
p
K
K
= =
+
6. STABILITY ANALYSIS
1. If all the poles of the system lie in the left half of s plane then the system is stable
2. If there are non-repeated poles on the je axis, system is marginally stable.
3. If there are repeated poles of the system on je axis system is unstable.
4. If there is one or more than one pole in R.H. of S plane system is unstable.
The system is said to be stable if.
(i) Bounded input gives bounded o/p
(ii) op should reduce to zero when input is removed Rouths Stability Criterion
States In order to determine the existence of a root having positive real port of a polynomial
equation given by
1 2
0 1 2
0
n n n
n
a s a s a s a
+ + + =
The rows consisting of alternate coefficients of polynomial are formed as follows
a
0
a
2
a
4
a
6
---------
a
1
a
3
a
5
a
7
---------
and the following array is formed
s
6
a
0
a
2
a
4
a
6
s
5
a
1
a
3
a
5
0
s
4
b
1
b
3
b
5
0
s
3
c
1
c
3
0 0
s
2
d
1
d
3
0 0
s
1
e
1
0 0 0
s
0
f
1
0 0 0
Where
1 2 0 2
1
1
a a a a
b
a
=
1 4 0 5 1 6 0
3 5 6
1 1
3 1 1 3 1 3 1 3
1 1
1 1
0 a a a a a a a
b b a
a a
a b a b c b b c
c d etc
b c
= = =
= =
The condition that all roots have negative red ports is given by
22
region of stability
T
t
a
1
a
2
> a
0
a
3
Q.1. A closed loop control system has the characteristic equation given by
s
3
+ 4.5s
2
+ 3.5s + 1.5 = 0
Investigate the stability using Rough-Hurwitz criterion
Solution : The Routh-array is formed as follows.
3 2
3
2
0
4.5 3.5 1.5 0
1 3.5
4.5 1.5
4.5 3.5 1.5 1
3.16 0
4.5
3.16 1.5 4.5 0
1.5 0
3.16
s s s
s
s
s
s
+ + + =
=
=
All the first column elements are of the same sign therefore the system is stable.
Q.2. The open loop transfer function of a feedback control system is given by
( 1)
( ) ( )
(1 )(1 2 )
K s
G s H s
s Ts s
+
=
+ +
The parameters K and T may be represented in a plane with K as the horizontal axis and T as vertical
axis determine the region in which the closed-loop system is stable
Solution : The characteristics equation is given by
1 + G(s)H(s) = 0
2Ts
3
+ (2 + T)s
2
+ (K + 1) s + K = 0
The rouths array is
3
2
0
2 1
2
2
( 1) 0
2
0
S T K
S T K
T
S K
T
S K
+
+
+
+
For stability
2 0, 2 0
0, 0
2
1 0
2
2 2(1 )
2 1
T T
K T
T
K
T
T K
K and T
T K
> + >
> >
+ >
+
+ +
< <
Therefore for stability we have
K > 0, T > 0, K > 1, T > 2
The region for stability is shown on fig.
Q.3. The characteristic equation of a feedback control system is
S
4
+ 20KS
3
+ 5S
2
+ 10S + 15 = 0
Find the range of K for which system is stable.
Solution : Rouths array is
23
4
3
2
2
1
0
1 5 15
20 10
1
5 15
2
600
10 0
10
15
S
S K
S
K
K
S
K
S
The system will be stable if
20K > 0, K > 0
2
1
1 1
5 0,
2 10
600
10 0
10
K
K
K
K
> >
>
2
600 100 10 0 K K + >
gives complex roots hence system is unstable
Q.4. The characteristic equation of a feedback control system is
S
3
+ 3KS
2
+ (K + 2) S + 4 = 0
Determine the range of K for which system is stable.
Solution : Rouths array is
S
3
+ 3KS
2
+ (K+2)S + 4 = 0
S
3
1 K + 2
S
2
3K 4
S
1
2
3 6 1
3
K K
K
+
S
0
4
For stability 3K > 0, K > 0
3K
2
+ 6K1 > 0, K > 1 1.53 K > .53
> K > .53
Q.5. Find out the conditions for stability for the systems. Whose characteristics equations are given below
the case where stability as suggested for real values of K determine the values of K which will cause
sustained oscillations
Find the frequency of oscillations
(a) s
4
+ 20s
3
+ 224s
2
+ 1240s + 2400 + K = 0
The Rouths array is
4
3
2
0
1 224 2400
20 1240 0
162 2400
(2400 )20
1240 0
120
2400
S K
S
S K
K
S
S K
+
+
+
+
For stability
2400 + K > 0, K > 2400
(2400 )20
1240 0
162
7644
2400 7644
K
K
K
+
>
<
< <
24
(b) S
3
+ (K + .5)S
2
+ 4KS + 50 = 0
Rouths array is
3
2
1
0
1 4
.5 50
50
4
.5
50
S K
S K
S K
K
S
+
+
For stability
K + .5 > 0, K > .5
.5
4 0
.5
K
K
>
+
4K(K + .5) > 50
2
12.5 0
2
K
K + >
K > 3.8 and K > 3.3
Therefore the condition for stability is
K > 3.8, K > .5, K > 3.3
Thus if K > 3.3 then all conditions are satisfied
If we put K = 3.3 then we has row as zero, the subsidiary equation for 8
2
row for K = 3.3 is
3.8s
2
+ 50 = 0
S = 3.63j
Thus frequency of oscillation is 3.63 rad/sec
Q.6. The open loop transfer function of a unity feedback control system is given as
( ) ( )
(1 )
K
G s H s
S TS
=
+
It is desired that all the roots of the characteristics equation must lie in the region to the left of the
line s = a, determine the value of K and T required so ie there are no roots to right of the line s = a
Solution : The characteristics equation is
1 + G(s)H(s) = 0
1 0
(1 )
K
S TS
+ =
+
2
1
0
S K
S
T T
+ + =
replace S by S a
(S a)
2
+
1
( ) 0
K
S a
T T
+ =
2 2
1
2 0
K a
S a S a
T T T
| | | |
+ + + + =
| |
\ . \ .
The rouths array is
2 2
0 2
1
1
2 0
K a
S a
T T
S a
T
K a
S a
T T
+
| |
+
|
\ .
+
If no root is to lie on the line S = a, then the first column of the Rouths array should have no sign
change
25
R(s)
C(s)
K(s+1)
s +as +2s+1
3 2
E(s)
2 2
2
1 1
2 0, 2
1 1
,
2 2
0
(1 )
0
1
2 2
a a
T T
T or aT
a
K a K a
a a
T T T T
K a a T K a aT
aT K a
a
If aT K
| |
+ > >
|
\ .
< <
+ > >
> >
= >
= >
Q.7. A system oscillates with frequency e if it has poles at s = je and no poles in the right half s-plane
determine the value of K and a so that the system shown in fig oscillates at a frequency 2 rad/sec
Solution : 1 + G(H)H(S) = 0
3 2
( 1)
1 0
2 1
K s
S as s
+
+ =
+ = +
S
3
+ as
2
+ (K + 2) s + K + 1 = 0
3
2
1
0
1 2
1
( 1)
2
1
S K
S a K
K
S K
a
S K
+
+
+
+
+
The system will have sustained oscillation when
1
2 0
1
2
K
K
a
K
a
K
+ | |
+ =
|
\ .
+
=
+
The auxiliary equation of row 2
2 2
2
2
( 1)
( 1) 0
( 1)
( )
1
2 / (2 )
1 1 1 1
2
4 2 4 2
1 2 1 3
.75 .75
4 4 4
K
as K s
a
K
s j j
a
K
r se j
a
K K K K
a a K
K K
K
a a a
e e
e
+
+ + = =
+
= =
+
= =
+ + + +
= = = =
+ +
+ +
= = = = =
26
7. ROOT LOCUS
Rule (1) Obtain the open-loop poles and closed loop poles from their respective transfer functions
Rule(2) The no of poles or the order of characteristic equation give the no of loci
Rule(3) Each locus starts at an open loop pole when K=0 and terminates at open-loop zero when K=
Rule(4) Root loci lither moves along the real axis or can happen to be as complex conjugate pains
Rule(5) A value of 8 on the real axis is a point on the root-locus if the total no of poles and zeros on
the real axis to the right of the point is odd i.e while constructing the root-loci on the real axis
choose a test point on it. If the sum of poles and zeros to the right of this point is odd then this
point is a part of the root-loci
Rule(6) The Break away point from the real axis is obtained by differentiating the open-loop transfer
function with respect to s and equating it to zero.
Rule(7) As one moves for enough away from the open-loop poles and zeros the root loci become
asyptatic to lines making angles an to the real axis
n
n
p Z
t
o =
P = No. of open-loop poles
Z = No. of open-loop zeros
n = an odd integer
Rule(8) The Intersection of asymptotes with the real axis at point s is given by
poles zeros
s
p z
E E
=
Rule(9) Intersection of the root loci with the imaginary axis can be easily obtained by use of Routh
criterion or by putting s = je and equating imaginary parts to zero to find e the intersection
Rule(10) Angles of departure and arrival of a root loci can be determined from the complex poles and
zeros respectively and is given by 180 - |
p
- |
z
Q.1. The forward path transfer function of a unity feedback system is given by ( )
( 4)( 5)
K
G s
s s s
=
+ +
sketch the root locus as k varies from zero to infinity
Solution : step 1
No of poles S = 0, 4 & 5
No. Zeros = 0
Step 2 The root locus exists between S = 0 & s = 4 and to the left of 5 mark the root locus on real
axis
Step 3 Number of root loci
P = 3 Z = 0
No of root loci (N) = 3
Step 4 Centroid of asymptotes
A
sumof poles sumof zeros
p Z
o
=
(0 4 5) 0
3
3 0
A
o
= =
Step 5 Angle of asymptotis
2 1
180
k
p Z
|
| | +
=
|
\ .
K = 0 |
1
= 60
K = 1 |
2
= 180
27
3
4
60
60 5
4.447j
+4.4j
+5j
5j
K = 2 |
3
= 300
Step 6 Calculation of break away point
The characteristic equation
1 + G(s)H(s) = 0
1 0
( 4)( 5)
k
s s s
+ =
+ +
3 2
2
1 2
9 20
3 18 20 0
1.4725, 4.5275
K s s s
dk
s s
ds
s s
=
= =
= =
Since 4 to 5 is not the segment of root locus therefore we consider 1.4725 as a breakaway point
Step 7 Determination of point of intersection of branches of root locus with imaginary axis by routh
Hurwitz.
s
3
+ 4s
2
+ 20s + K = 0
3
2
0
1 20
9
180
9
s
s K
k
s
s k
For K = 180 the auxiliary
9s
2
+ K = 0, 9s
2
+ 180 = 0 s = j4.47
Q.2. For a unity feedback system the open loop transfer function is given by
2
( )
( 2)( 6 25)
k
G s
s s s s
=
+ + +
(a) Sketch the root locus for 0 s K s
(b) At what value of K the system becomes unstable
(c) At this point of instability determine the frequency of oscillation of the system.
Solution : Step 1 plot the Poles and zeros
Poles are at S
1
= 0, S
2
= 2, s
3
= 3 + 4j, s
4
= 3 4j
s
2
+ 6s + 2s = 0
s
3
= 3 + 4j
s
4
= 3 4j
Step 2 The segment on the real axis between s = 0 & s = 2 is the part of the root locus
Step 3 No of root loci
No of poles p = 4
No of zeros = z = 0
No of root loci N = P = 4
Step 4 Centroid of the asymptotes
(0 2 3 4 3 4 0
2
4 0
A
sumof poles sumof zeros
p z
j j
o
=
+
= =
Step 5 Angle of asymptotes
2 1
180
2
K
P
|
+
=
28
1
2
2 0 1
0 180 45
4
2 1 1
1 180 135
4
K
K
|
|
+
= = =
+
= = =
3 3
4
2 2 1
2 180 225
4
2 3 1
3 180 315
4
K
K
| |
|
+
= = =
+
= = =
Step 6 Breakaway point
1 + G(s)H(s) = 0
4 3 2
2
4 3 2 3 2
3 2
1 0 8 37 50 0
( 2)( 6 2 )
( 8 37 50 ) (4 24 24 50) 0
4 24 74 50 6
K
K s s s s
s s s s s
dk
K s s s s s s s
ds
s s s
+ = + + + + =
+ + +
= + + + = + + + =
+ + + =
by trial & error method
S = .8981*
Step 7 Determination of je crossover (by Routh Hurwitz)
S
4
+ 8s
3
+ 37s
2
+ 50s + k = 0
4
3
2
0
1 37
8 50
30.75
1537.5 8
30.75
1537.5 8
0 192.18
30.75
s k
s
s k
k
s
s k
k
k
= =
K = 192.18 Auxiliary equ
30.75s
2
+ K = 0
30.75s
2
= 192.18
S = 2.5j
Step 8 (a) Angle of departure from upper compex angle
|
d
= 180 (104 + 90 + 127)
|
d
= 141
(b) The range of values for stability is 0 < K < 192.18
The closed loop system becomes unstable for K > 0 & K > 192.18
(c) At this point of instability the gain is K = 192.18
30.75s
2
+ 192.18 = 0
S = je
30.75 e
2
+ 192.18 = 0
e = 2.5 rad/sec
The frequency of oscillation at the point of instability = 2.5 r/sec the root locus plot is shown fig.
Q.3. Consider a unity feedback control system with the following feed forward transfer function
2
( )
( 4 8)
K
G s
s s s
=
+ +
Plot the root locii for the system
29
Solution :
Step 1 Plot the poles & zeros
S
2
+ 4s + 8 = 0
2 3
4 16 32
,
2
2 2
s s
j
=
=
There poles are at s
1
= 0, s
2
= 2 + 2j, s
3
= 2 2j
Step 2 Since there is only one pole at s = 0 the entire left half of the real axis is the port of the root
locus.
Step 3 No of root loci
No of poles P = 3
No of zeros Z = 0
No. of root loci N = P = 3
Step 4 Centroid of the asymptotes
2
(0 2 2 2 2 ) 0 4
1.33
3 3
A
sumof poles sumof zeor
P
j j
o
=
+
= = =
Step 5 Angle of asymptotes
2 1
180
K
P Z
|
+
=
K = 0 |
1
= 60
K = 1 |
2
= 180
K = 2 |
3
= 300
Step 6 Breakaway point
1 + G(s)H(s) = 0
2
3 2
3 2
2
2
1 0
( 4 8)
4 8 0
( 4 8 )
(3 4 8)
3 8 8 0 1.33 .943
K
s s s
s s s k
K s s s
dk
s s
ds
s s s j
+ =
+ +
+ + + =
= + +
= + +
+ + = =
The angle condition is not satisfied hence there is no. breakaway point on the real axis
Step 7 Point of intersection with imaginary axis
The characteristic equation
S
3
+ 4s
2
+ 8s + k = 0
Routh array is
3
2
1
0
1 8
4
32
4
S
S K
K
S
S K
For sustained oscillation 32 K = 0, K = 32
4S
2
+ 32 = 0 S = 2.83j
Step 8 The angle of departure from the upper complex pole is
30
180 (135 90 ) 45
d
| = + =
Q.4. Plot the root loci for the closed loop control system with
2
( ) ( ) 1
( 1)( 4 5)
K
G s H s
s s s s
= =
+ + +
Solution Step 1 Plot the poles and zeros.
S(s+1) (s
2
+ 4s + 5) = 0
S = 0, 1, 2 + j, 2j
Step 2 The segment b/e s = 0, & s = 1 is the fort of the root locus on real axis
Step 3 No of root loci
No of root loci N = P = 4
Step 4 Centroid of the asymptotes
A
sumof poles sumof zeros
P Z
o
=
0 1 2 2 0 5
1.25
4 4
j j +
= = =
Step 5 Angle of asymptotes
2 1
180
K
P Z
|
+
=
K = 0 |
1
= 45
K = 1 |
2
= 135
K = 2 |
3
= 225
K = 3 |
4
= 315
Step 6 Breakaway point
1 + G(s)H(s) = 0
2
4 3 2
4 3 2
1 0
( 1)( 64 5)
5 9 5 0
( 5 9 5 )
K
s s s s
s s s s K
K s s s s
+ =
+ + +
+ + + + =
= + + +
Breakaway point is s = .4
Step 7 Angle of departure at the upper complex pole
180 (154 136 90 ) 200
d
| = + + =
Step 8 Point of intersection on je axis
s
4
+ 5s
3
+ 9s
2
+ 5s + k = 0
s
4
1 9 k
s
3
5 5
s
2
8 k
s
40 5
8
k
s
0
K
At 40 5k = 0, K = 8 (for sustained oscillation) the auxiliary equation
A(s) = 8s
2
+ k
8s
2
+ 8 = 0
S = j
Q.5. A unity feedback system has an open loop transfer function
( 1)
( )
( 1)
K s
G s
s s
+
=
31
Breakaway
Point 2.414
Re-entry
Point .414
1
j
+j
2 1 0
sketch the root locus plat with k' as variable parameter and show that the loci of complex roots are
port of a circle with (1, 0) as centre and radius = 2
Solution : Step 1 Plot the poles & zero
Poles s
1
= 0, s
2
= 1
Zeros s
3
= 1
Step 2 Centroid of asymptotes
0 1 ( 1)
2
2 1
A
sumof poles sumof zeros
p z
o
=
=
+
= =
Step 3 Angle of asymptotes
2 1
180
K
p z
|
+
=
2 0 1
0, 180 180
2 1
k |
+
= = =
Step 4 Breakaway point
2
( 1) ( 1)
1 0
( 1) 1
2 1 0 2.414 & .414
k s s s
k
s s s
dk
s s s
ds
+
+ = =
+
= + = =
Since both values are the part of the root locus, hence there will be a breakaway point and other is re-
entry of breaking point
2
2.5 2
d k
dt
= +
put s = 2.414
2
2
2.828
d k
ds
=
2
2
d k
dr
is negative for s = 2.414 hence it is a breakaway point
put s = .414
2
2
d k
ds
is positive
It is a re-entry point
Step 5 point of intersection on imaginary axis characteristic equation
s
2
+ (k 1) s + 1 = 0
s
2
1 1
s k 1 0
s
0
1
32
R
e
I
m
1+j0
V
jv
For stability k 1 > 0
K > 1
Auxiliary A(s) = s
2
+ 1
s = j
8. NYQUIST STABILITY CRITERION
This is a graphical method of determining the stability of a system consider the system whose clased loop
transfer function is
( ) ( )
( ) 1 ( ) ( )
C s G s
R s G s H s
=
+
( ) ( )
( ) 1 ( ) ( )
C j G j
R j G j H j
e e
e e e
=
+
We know that for stability all roots of the characteristic equation 1 + G(s)H(s) = 0
must be lie on the left hand side of the s-plane
Nyquist stability criterion relates the no of zeros and poles of 1+G(s)H(s) i.e lie on the R.H.S of s-plane to
the open-loop frequency response G(je)H(je)
Polar plot of G(je)H(je) is drawn Nyquist plot is obtained by drawing its mirror image e varies from to
and no of encirdements of point 1 + j0 is observed.
N = pz
N = No of encirdements of point 1 + j0
P = No of poles of G(s)H(s) that are on the right half of s-plane for stability of closed loop z should be zero
N = p
Q.1. Using Nyquist criterion determine the stability of of the feedback system which has the following
open loop transfer function
2
( ) ( )
(1 )
k
G s H s
s ST
=
+
Solution : Put s = je
2
2 2 2 2 2
( ) ( )
( ) (1 )
( ) ( )
(1 ) (1 )
k
G j H j
j j T
k k
G j H j j
T T
e e
e e
e e
e e e e
=
+
= +
+ +
the Nyquist diagram is shown in the fig because of the double pole at s = 0 a small semicircular
detour at the origin should be made the point (-1 + j0) is encided twice hence N = 2
P = 0
Z = 2
hence the system is unstable.
33
R
e
I
m
jv
180
A 0
90
Q.2 Use Nyquist criterion determine whether the closed loop system having the following open loop
transfer function is stable or not
1
( ) ( )
(1 2 )(1 )
G s H s
s s s
=
+ +
Solution : s = je
2
2 2 2 2
1
( ) ( )
(1 2 )(1 )
3 (1 2 )
( ) ( )
(1 4 )(1 ) (1 4 )(1 )
G j H j
j j j
G j H j j
j
e e
e e e
e
e e
e e e e e
=
+ +
=
+ + + +
Equate the imaginary port to zero we get the point of intersection on real axis
1 2e
2
= 0
e = .707
Since OA = .66 the point (1 + j0) is not encircled
N = 0
P = 0
Z = 0
hence the system because no closed loop poles lie in the right half of s-plane
Q.3. The open loop transfer function of a unity feedback system is given by
1 2
( )
(1 )(1 )
k
G s
s ST ST
=
+ +
Derive an expression for gain k in terms of T
1
, T
2
and specified gain margin
Solution :
1 2
( )
(1 )(1 )
k
G s
s ST ST
=
+ +
s = je
1 2
2
1 2 1 2
2 2 2 2 2 2 2 2
1 2 1 2
2
1 2
1 2
1 2
1 2 1 2
( )
(1 )(1 )
( ) (1 )
( ) ( )
(1 )(1 ) (1 )(1 )
0
(1 ) 0
1
1
( ) ( )
m
k
G j
j j T j T
k T T jk TT
G j H j
T T T T
I
k TT
TT
KTT
G j H j
T T TT
e
e e e
e
e e
e e e e e
e
e
e e e
=
+ +
+
=
+ + + +
=
=
=
= =
+
34
gain margain
1
m
G
a
=
1 2 1 2
1 2 1 2 1 2
2 2 2 2
1 2
1 1
1 2
0 0
1 1 1
( )
1
( ) ( )
1 1
. ( ) ( ) 90 tan tan
lim ( ) ( ) lim ( ) ( ) 90
lim ( ) ( ) 0 lim ( ) ( ) 270
m
m
kTT T T
a G k
T T k TT G T T
G j H j
T T
G j H j T T
G j H j G j H j
G j H j G j H j
e e
e e
e e
e e e
e e e e
e e e e
e e e e
| | +
= = = +
|
+
\ .
=
+ +
=
= =
= =
Q.4. The open-loop transfer function of a control system is given by
( )
( 2)( 10)
k
G s
s s s
=
+ +
Determine the value of k so that the system may be stable with
(a) Gain margin equal to 6 db
(b) P.M equal to 45
Solution :
10
1
20log GM
a
=
`
)
10
1
20log
( )
( 2)( 10)
a
k
G s s j
s s s
o
e
=
`
)
= =
+ +
2 3
2 2 2 2 2
( )
( 2)(10 )
12 (20 )
( )
(4 )(100 ) (4 )
k
G j
j j j
k jk
G j
e
e e e
e e e
e
e e e e e
=
+
=
+ + +
to get the point of intersection on real axis, equate the imaginary part to zero.
3
2 2 2
4.47
(20 )
0
(4 )(100 )
4.47 /
( ) .0041
k
r se
G j k
e
e e
e e e
e
e
=
=
+ +
=
=
Put e = 4.47 rad/sec
35
I
m
Real
.0041 k = .501
a =.502
k = 122
(ii) . ( ) ( ) 180 PM G j H j e e = +
1 1
1 1
45 90 tan tan 180
2 10
tan tan 45
2 10
2 10
1
1
2 10
e e
e e
e e
e e
= +
+ =
+
=
2
12 20 0
13.48, 1.48
e e
e
+ =
=
Consider the positive value of e i.e e = 1.48 r/se
( ) 1
1
(2 )(10 )
1
1.48(2 1.48 )(10 1.48)
37.22
G j
k
j j j
k
j j j
k
e
e e e
=
=
+ +
=
+ +
=
Q.5. Construct the complete Nyquist plot for a unity feed-back control spstem whose open-loop transfer
function is
2
( ) ( )
( 2 2)
k
G s H s
s s s
=
+ +
Find maximum value of k for which the system is stable.
Solution :
{ }
2
( ) ( )
( ) 2 2
k
G j H j
j j j
e e
e e e
=
+ +
2
1
2
2 2 2
{2 2 }
2
tan 90
2
(2 ) 4
k
j j
k
M
e e e
e
|
e
e e e
=
+
= =
=
+
When 0 90 GH e = =
0 270
1 153.43
5
2 206.8
2 18
GH
k
GH
k
GH
e
e
e
= =
= =
= =
36
real
I
m
Phase crossover frequency
1
2
1
2
2
180 tan 90
2
2
tan 90
2
e
e
e
e
2
( 2)
2
2 0 2
4
2 (2 2) 4 2
k k
M
e
e e
= =
= =
+
For stability 1
4
k
<
K < 4
Q.6. sketch the Nyquist plot for a certain unity feedback system having an open-loop transfer function
given by
( )
(1 )(1 2 )(1 3 )
k
G s
s s s s
=
+ + +
Determine the range of values of k for which the system is stable.
Solution :
1 1 2
2 2 2
90 tan tan 2 tan 3
1
1 1 4 1 9
0, 90
, 360
M
| e e e
e e e e
e |
e |
=
=
+ + +
= =
= =
( )
(1 )(1 2 )(1 3 )
k
G j
j j j j
e
e e e e
=
+ + +
Rationalising and equating the imaginary part to zero, we get 11e
2
= 1
e = .30 r/sec
2 2 2
/ .3
.50
.3 1 .3 1 4 .3 1 9 .3
k k
M e = = =
+ + +
for stability
1 .50
.5
k
K > <
37
9. BODE PLOTS
A sinusoidal transfer function may be represented by two separate plats one giving the magnitude versus
frequency and the other the phase angle
A bade diagram consists of two graph one is a plot of the logarithm of the magnitude of a sinusoidal transfer
function the other is a plot of the phase angle both are plotted against the frequency in logarithmic scale the
main advantage of using the logarithmic plot is that multiplication of magnitudes can be converted into
addition
The logarithmic representation is useful in that it shows both the low and high frequency characteristics of
the transfer function in one diagram expanding the low-frequency is very advantageous since characteristics
at low frequencies are most important in practical systems.
Although it is not possible to plot the curves right down to zero frequency because of the logarithmic
frequency (by 0 = ) This dog not create a serious problem basic factors of G(je)H(je)
As started earlier the main advantage in using the logarithmic plot is in the relative case of plotting
frequency response curves.
The basic factors that very frequency occur in a arbitrary transfer function G(je)H(je) are
1. Gain k 2. Integral and derivative factors (je)
1
3. First-order factors (1 + je)
1
4. Quadratic factors
1
2
1 2 ( / ) ( / )
n n
j j c e e e e
( + +
The Gain k A number greater than unity has a positive value in decibels, While a number smaller
than unity has a negative the log-magnitude curve for a constant gain k is a horizontal straight line at the
magnitude of zolyk decibels the phase angle of the gain k is zero. The effect of vary the gian k in the transfer
function is that it raises or lowers the log magnitude curve of the transfer function by the corresponding
constant amount but it has no effect on the phase angle
Integral and derivative factors (je)
1
The logarithmic magnitude of
1
je
in decibels is
1
20log 20log
( )
db
j
e
e
=
The phase angle of
1
je
is constant and equal to 90
In bode diagrams frequency ratios are expressed in terms of octaves or decades. N octave is a frequency
band from e
1
to 2e
1
where e
1
is any frequency value a decade is a frequency band from e
1
to 10e
1
where
gain e
1
is any frequency
Q.1. Find slope of magnitude plot after e > 100 in a system having
5( 2))
( ) ( )
( 100) 1)
100 1
1
20
20
100 1 (1 ) 1 (1 )
100 100
s
G s H s
s s s
s
s
s s
s s s s
+
=
+ +
| |
+
+ |
\ .
= =
| | | |
+ + + +
| |
\ . \ .
1 1 1
90 tan tan tan
20 100
20 /
GH
zero p dB decade
e e
e
= +
+
and pole p 20dB/decade
For e > 100 slope of magnitude plot 20 20 + 20 20 = 40 dB/decade
Note for e < 1
38
Slope = 20 dB/decade
1 < e < 20
Slope = 20 20 = 40 dB/decade for 20 < e < 100
Slope = 20 20 + 20 = 20 dB/decade
The following are the advantages of Bode plot
(1) Plotting of bode plot is relatively easier as compared to other methods or the loci of (1 + ST) and
1
k
ST
| |
|
+
\ .
can be represented by straight line asymtates.
(2) Multiplication is converted into addition, so if
( )
(1 )
k
G s
s ST
=
+
Putting s = je
20 log |G(je)| = 20 log k 20log |je| 20 log |(1 + jeT)|
(3) Low and high frequencies characteristics can be represented on a single diagram
(4) Study of relative stability is easier as parameters of analysis of relative stability are gain and phase
margin which are visibly seen on sketch
(5) If modification of an existing system is to be studied. It can be easily done on a bade plot.
Basic terms that appear in a transfer function and method of plot-ting them is described below
(1) Constant term k It gives e constant magnitude of 20 log k it does not give any phase shift. It is
represented by a line parallel to odb line (slope 0 dB/dec) and starts from a point having a magnitude
20 log k
(2) (s)
1
Its magnitude is 20 log e it is a straight line having a slope of 20dB/sec and posses through e
= 1 rad/sec where its magnitude is odB
(3) (1 + ST)
n
magnitude is given by n 20 log [1 + jeT] having a slope of 20 n dB/dec. Asymptotes
are approximated by
(a) eT = < 1 magnitude is n20 log
1 ii
odB
(b) eT >> 1 magnitude is n 20 log eT
It has a slope of n 20 logeT = 0
eT = 1
1
T
e =
Which is called the corner frequency due to approximation maximum error of 3dB. Occurs at the
corner frequency exact plot can be drown log finding the magnitude one octave to the left and right
of corner frequency.
(4) s
2
+ 2c e
n
s + e
n
(a) If c > 1 it can be reduced to two first order factor
(b) If c < 1 the magnitude is
2
1
2
2
2 2
2
20log 1 2
20log 1 4
n n
n n
j
e e
c
e e
e e
c
e e
| |
= +
` |
\ .
)
| | | |
= +
` ` | |
\ . \ .
)
)
This term is approximated by drawing two straight lines corner frequency is e
n
below e
n
line
follows odB line and beyond e
n
it has a slope of 40 dB/dec
Error due to approximation depends upon the value of c is small the error is large
(5) Phase plot It the transfer function is as given before
39
20 dB/dec fine
due to factor 1
s
2
60 dB/dec
20dB/dec
fine due to
factor
1
1+.5s
Phase Plot
Phase cross over
frequency = 5 rad/sec
20dB/dec
40dB/dec
Gain cross over frequency = 4.2 r/sec
10
100
magnitude plate
2 3 4 1
40
3 4 5 6 7 2
20
0
20
80
100
120
220
DB
2 2
2
1 1 1
1 2 2
2
(1 )
( )
(1 )( 2 )
2 /
( ) 90 tan tan tan
1
n n
n
n
k ST
G s
s ST s s
G j T T
ce e
ce e
e | e e
e
e
+
=
+ + +
= = +
Q.2. Sketch the bode plots and determine the gain cross over and phase crossover frequencies.
10
( )
(1 .5 )(1 .1 )
G s
s s s
=
+ +
Solution : Corner frequencies
The corner frequencies are 2 and 10 magnitude plot
Factor Corner
frequency
Asymptotic log-magnitude characteristic
1 1
s
None Straight line of constant slope 20dB/dec passing e = 1
2 1
1 .5s +
e
1
= 2 Straight line of constant slope 20dB/dec passing e
1
= 2
3. 1
1 .1s +
e
2
= 10 e
2
= 10
4. 10 None Straight line of constant slope of 0 dB/dec starting from 20
log10 = 20dB point
Magnitude plots for individual factors are shown by dotted line resultant line is shown by a firm line
phase plot
| = 90 tan
1
.5e tan
1
.1e
Ser No
e |
1 0 90
2 .1 93.43
3 1 122.3
4 2 146.31
5 5 184.76
6 10 213.7
7 15 228.7
Gain cross over frequency = 4.2 rad/sec
Phase crossover frequency = 4.5 r/sec
40
1
5
10 50
28dB
2
0
d
B
/
d
e
c
l
in
e
d
u
e
T
o
f
a
c
t
o
r
2
0
d
B
/d
e
c
li
n
e
d
u
e
T
o
f
a
c
t
o
r
0 dB/dec
20 dB/dec
40 dB/dec
+40 dB/dec line due
To factor
1
s
2
40
20
.1
20
40
60
dB
Q.3. Sketch the bode plot for the transfer function
2
( )
(1 .2 )(1 .02 )
ks
G s
s s
=
+ +
Determine the system gain k for the gain cross-over frequency to be 5rad/sec
Solution :
Let k = 1 then
2
( )
(1 .2 )(1 .02 )
s
G s
s s
=
+ +
Corner frequencies The corner frequencies
are 5 and 50 r/sec
Magnitude plot
Ser. No. Factor Corner frequency Asymptotic log magnitude
1 S
2
None Straight line of constant slope 40
dB/dec passing e = 1
2 1
1 .2s +
e
1
= 5 20 dB/dec e = 5
3 1
1 .02s +
e
2
= 50 20 dB/dec e = 50
The magnitude plot in shown in fig if the gain cross over frequency is required to be 5 rad/se then the
magnitude plot must cross the 0 dB line at 5 rad/sec for this the plot has to be brought down by 28 dB hence
20 log k = 28
k = .04
41
20dB/dec
20dB/dec
12
dB
2.5 10 25
20dB/dec
20dB/dec 0dB/dec
20dB/dec
40dB/dec
2 4 8 24 36
dB
Q.4. Find the open-loop transfer function of a system whose approximate plot is shown in fig.
Solution : Corner frequencies are
e
1
= 2.5, e
2
= 10, e
3
= 25
change in magnitude in dB
= slopex (No of decades b/e two fre)
= 20(log 2.5 log 1) = 20 log 25
= 7.95
Magnitude = 12 + 7.95 = 4.05dB
20 log k = 4.05
K = .63
Since first line has a slope of 20 dB/dec and starts from a point 4.05 dB at e = 1 rad/sec the factor
contributing this is
.63 k
s s
=
plot b/e e = 2.5 and e = 10 is having a slope of 0 dB/dec at e = 2.5 the slope has changed from 2.5
the slope has changed from 20 dB/dec to 0 dB/dec and this can only happen due to a factor in the
numerator and is ( ) 1 1 .4
2.5
s
s
| |
= + = +
|
\ .
at e = 10 the slope has changed from 0 dB/dec to +20
de/dec and is due to a factor is the numerator and is 1 (1 .1 )
10
s
s
| |
= + = +
|
\ .
at e = 25 the slope has
changed from + 20 dB/dec to 0 dB/dec and is due to a factor in the denominator and is
1 (1 .04 )
25
s
s
| |
= + = +
|
\ .
the open loop transfer function is thus
.63(1 .4 )(1 .1 )
( )
(1 .04 )
s s
G s
s
+ +
=
+
Q.5. From the Asymptotic magnitude (in dB) versus frequency (by scale) plot of fig find the associated
transfer function assume no right half plane poles or zeros present.
Solution :
42
20dB/dec
9
20dB/dec
1 20 40
dB
(1) Slope of the first line is 20 dB/sec indicating a term
1
s
(2) At e = 2 rad/sec slope charges to a 0 dB/dec indicating a term 1 (1 .5 )
2
s
or s
| |
+ +
|
\ .
in the numerator
(3) At e = 4 rad/sec slope changes to + 20 dB/dec indicating term 1 (1 .25 )
4
s
or s
| |
+ +
|
\ .
in the numerator
(4) At e = 8 rad/sec slope charges to 0 dB/dec indicating a term 1 (1 .125 )
8
s
or s
| |
+ +
|
\ .
in the denominator
(5) At e = 24 rad/sec slope change to 20 dB/dec indicating a term 1 (1 .042 )
24
s
or s
| |
+ +
|
\ .
in the
denominator
(6) At e = 36 rad/sec slope change to 40 dB/dec indicating a term 1 (1 .028 )
40
s
or s
| |
+ +
|
\ .
in the
denominator
20 log k = 20 log 8
k = 8
8(1 .5 )(1 .25 )
( )
(1 .125 )(1 .042 )(1 .028 )
s s
G s
s s s s
+ +
=
+ + +
Q.6. Find the transfer function
Solution : First line has a slope of 20 dB/dec and is not passing through e = 1 rad/sec therefore it
indicates a term
k
s
20 log k = 9
k = .35
the term is
.35
5
at 1 / sec rad e = slope change to 0 dB/dec indicating a terms (1 + s)
at e = 20 rad/sec, slope charges to +20 dB/dec indicating a term 1 (1 .05 )
20
s
or s
| |
+ +
|
\ .
at e = 40
rad/se slope change to 0 dB/dec indicating a term
1 1
(1 .025 )
1
40
or
s
s
| |
|
|
+
|
+
\ .
.35(1 )(1 .05 )
( )
(1 .025 )
s s
G s
s s
+ +
=
+
43
10. LAPLACE TRANSFORM
0
( ) ( )0
st
F s s t dt
=
}
Derivation of Laplace transform
(1)
0
1
at at st
Le e e dt
s a
= =
}
(2)
1
1
at
L e
s a
(3) f(t) = e
at
put a = je
1
cos sin
j
j
Le
s j
e t j t
e
e
e
e e
=
= +
2 2
1
(cos sin )
s j
L t j t
s j s
e
e e
e e
+
+ = =
+
2 2
2 2 2 2
1 1
2 2 2 2
(cos )
cos sin
cos sin
s j
L t j t
s
s
L t L t
s s
s
L t L t
s s
e
e e
e
e
e e
e e
e
e e
e e
+
+ =
+
= =
+ +
= =
+ +
(4) In the function f(t) = e
st
( ) ( )
( )
at j t j t
a j
e e f t e
o e o e
o e
+ +
= +
= =
( )
1 1
( ) ( )
j t
Le
s j s j
o e
o e o e
+
= =
+ +
( )
2 2
2 2 2
1 1
2 2 2 2
(cos sin )
1 ( )
(cos sin )
( ) ( )
cos sin
( ) ( )
cos sin
( ) ( )
j t at
at
t t
t t
e e t j t
s j
Le t j t
s j s
s
Le t Le t
s s
s
L e t L e t
s s
o e
o o
o o
e e
o e
e e
o e o e
o e
e e
o e o e
o e
e e
o e o e
+
= +
+ +
+ = =
+ + +
+
= =
+ + + +
+
= =
+ + + +
(5) In the function f(t) = e
at
put a = 1
f(t) = e
t
1
5 1
t
Le =
Table of L.T
f(t) f(s) = L{f(t)}
(1) f(t) unit impulse at t = 0 1
44
(2) u(t) unit step at t = 0
1
s
(3) u(t T) unit step at t = T
1
sT
e
s
(4) t
2
1
s
(5)
2
2
t
3
1
s
(6) t
n
1 n
n
s
+
(7)
at
e
1
s a +
(8) e
at
1
s a
(9) te
at
2
1
( ) s a +
(10) te
at
2
1
( ) s a
(11) t
n
e
at
1
( )
n
n
s a
+
+
(12) sin et
2 2
s
e
e +
(13) cos et
2 2
s
s e +
(14) e
ot
sin et
2 2
( ) s
e
o e + +
(15) e
ot
coset
2 2
( )
s
s
o
o e
+
+ +
(16) sinhdt
2 2
s
o
o
(17) coshat
2 2
s
s a
Basic Laplace transform theorems
(1) LT of linear combination { }
1 2 1 2
( ) ( ) ( ) ( ) L af t bf t aF s bF s + = +
(2) If the Laplace transform of f(t) is F(s) then
(i)
( )
( ) (0 )
df t
L sF s f
dt
+
=
(ii)
2
2 1
2
( )
( ) (0 ) (0 )
d f t
L s F s sf f
dt
+ +
=
(iii)
3
3 2 1 11
3
( )
( ) (0 ) (0 ) (0 )
d f t
L s F s s f sf f
dt
+ + +
=
(3) If the Laplace transform of f(t) is F(s) then
(i)
1
( ) (0 )
( )
F s f
L f t
s s
+
(
= +
(
}
45
(ii)
1 2
2 2
( ) (0 ) (0 )
( )
F s f f
L f t
s s s
+ +
(
= + +
(
}}
(iii)
1 2 3
3 3 2
( ) (0 ) (0 ) (0 )
( )
F s f f f
L f t
s s s s
+ + +
= + + +
}}}
(4) If the LT of f(t) is F(s) then Le
at
f(t) = F(s + a)
(5) if the LT of f(t) is F(s)
( )
( )
dF s
Ltf t
ds
=
(6) Initial value theorem
0 0
lim ( ) lim ( ) lim ( ) lim ( )
t s t s
f t s Lf t f t sF s
= =
(7)
0 0
lim ( ) lim ( ) lim ( ) lim ( )
t s t s
f t sLf t f t sF s
= =
Q.1. Find the invercese LT of the following functions
(i)
1
( )
( 1)
F s
s s
=
+
1 1 1
1
1 1 1
( 1) 1
1
(1 )
( 1)
t
L L L
s s s s
L e
s s
=
+ +
=
+
(ii)
2
6 6
( 4 3) ( 1)( 3)
s s
s s s s s s
+ +
=
+ + + +
1 1
3
1
2 2.5
2
( )
5 1 3
( ) 2 2.5 .5
t t
L F s L
s s
f t e e
= +
+ +
= +
Q.2. Use the Laplace transform to solve the differential equation
2
2
( ) ( )
6 8 ( ) 2 ( )
( ) 1, '(0) 2
d v t dv t
v t t
dt dt
v o v
+ + =
= =
Solution : We take the L.T of each term in given differential equation
| |
| |
2
2
2
( ) (0) '(0) 6 ( ) (0) 8 ( )
(0) 1, '(0) 2
2
( ) 5 2 6 ( ) 1 8 ( )
s V s sV V SV s V V s
S
V V
s V s sV s V s
s
+ + =
= =
+ + + =
2
0 2 4
4 2
( )
( 2)( 4) 2 4
1 1 1
( ) / ( 2) ( ) / ( 4) ( ) /
4 2 4
s s s
s s A B C
V s
s s s s s s
A sV s B s V s C s V s
= = =
+ +
= = + +
+ + + +
= = = + = = + =
1 1 1
4 2 4
( )
2 4
V s
s s s
= + +
+ +
by the Inverse L.T
46
Z
1
Z
2
Z
n
Y
1
Y
2
Y
p
2 4
1
( ) (1 2 ) ( )
4
t t
V t e e u t
= + +
Q.3. Solve for the response y(t) in the following integrodifferential equation
0
5 ( ) 6 ( ) ( )
(0) 2
t
dy
y t y d u t
dt
y
t t + + =
=
}
Solution : Taking the LT of each term, we get
{ }
{ }
2
6 1
( ) (0) 5 ( ) ( )
(0) 2
( ) 5 6 1 2
SY s Y Y s Y s
s s
y
Y s s s s
+ + =
=
+ + = +
2 1
( )
( 2)( 3)
s
Y s
s s
+
=
+ +
( )
1 2 3
3 5
( )
2 3
( ) 3 5 ( )
t t
Y s
s s
L Y s e e t
= +
+ +
= +
11. STATE VARIABLES
1
2
( )
( )
( )
( )
n
X AX BZ
x t
x t
X t
x t
= +
(
(
(
=
(
(
= state vector representing n state vectors and the dot represents the first
derivative with respect to time i.e
1 1
2 2
( ) ( )
( ) ( )
( ) ( )
: :
( ) ( )
n n
x t z t
x t z t
x t z t
x t z t
( (
( (
( (
= =
( (
( (
= Input vector representing m inputs
1
2
( )
( )
( )
:
( )
p
y t
y t
y t
y t
(
(
(
=
(
(
(
= the output vector representing P outputs
47
i
+
V
s R
V
L
+
L i
c
i
x
C
V
+
1
1 1
.
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
X Ax Bz
LT
SX s AX s BZ s SI A X s BZ s
X s SI A B Z s Y s CX s DZ s
Y s
H s C SI A B D H s C SI A B
Z s
= +
= + =
= = +
= = + =
A = system matrix B = Input coupling matrix
C = output matrix D = feed forward matrix
Q.1. Find the state-space representation of the circuit determine the T.F of the circuit when V
s
is the input
and in is the output take R = 1O, C = .25F, and L = .5H
Solution :
L
di
V L
dt
=
c x c
s L s
dv
i C i i i
dt
dv V V i
c i V
dt R Rc c
di
V V V L V V
dt
= = +
= = +
= + = +
| |
1 1
0
1
1
0
1
, 0
1 1
1, ,
4 2
1 1
0
4 4 0
1
, 0 1, 0
1
2 0 2 1
0
s
n
s
s
V V V
i i
L L R
V V
Rc c
V
i
i
L
L
V
i
i R
If R C L
Rc c
A B C
R
L
L
= + =
(
(
(
(
(
(
= + (
(
(
(
(
(
(
(
=
(
(
= = =
(
(
(
( (
(
(
= = = = = = (
( (
(
(
(
SI A =
0 4 4 4 4
0 2 0 2
s s
s s
+ ( ( (
=
( ( (
taking the inverse of this gives
48
+
i
i
0
i
1
6
+
V
0
+
V
1
3
F
V
s
V
i
| |
1
2
1
2 2
4
2 4 adjoint of A
( )
determinant of A 4 8
4 0
1 0
2 4 2 8
( ) ( )
4 8 4 8
s
s
SI A
s s
s
s
H s C SI A B
s s s s
(
(
+
= =
+ +
( (
( (
+
= = =
+ + + +
Q.2. Determine the state variable model and find the transfer function of the system
Solution :
1 1
0
1 0 1
0 1 1
1
0 6 6
6
2
2( ) 3 2
2
2 4 4
3
s s
s
s
s
s
i
V i i V i
V
V i V V i i
V i i V i V i
i V V
i i V i V
+ + = =
= + + = +
= = +
+
= = +
0
0 0 0
1 3
3
2 3 2
V
V i V V i = + =
( )
0 0
0
2
2
3 3
2
2
3
2 1 1 1
2 4 4 0
i s
s s i
s
s
V V i V V
i V i
V V i V V V i V V
V V V
i i i
+ | |
= =
|
\ .
= + = + +
( ( ( ( (
= +
( ( ( ( (
0
0
2 2 2
0
3 3 3
1 1
0 0
3 3
s
i
V V V
i V i
( (
( (
( ( (
= + ( (
( ( (
( (
( (
Controllability and OBSER VABILITY
Definition of controllability
A system is said to be controllable if the state of the system can be transferred to another desired state over a
given time period by using input
KALMANS TEST FOR CONTROLLABILITY
Consider
X AX DV = +
Then Q
c
= [B : AB : A
2
B : ------------ : A
n1
B]
Q
c
controllability matrix
According to Kalmans test
(i) System is completely controllable if rank of matrix Q
c
is equal to order of the system i.e (r = n)
(ii) System will not be completely controllable (un controllable) If rank of matrix Q
c
is less than order of
the system i.e (r = n)
Then no of uncontrollable states = n r
49
no. of controllable states = r
rank of matrix Q
c
= n. i.e r = n
If det Q
c
= 0
for 2
nd
order system
(1) Rank = 2 if |Q
c
| = 0
Rank = 0 if B = 0
Rank = 1 If both above condition fails for 3
rd
order system
(i) Rank = 3 if |Q
c
| = 0
(ii) Rank = 2 if even one of the cofactors any element ij 1 non zero.
(iii) Rank = 1 if even one of the elements of Q
c
is non zero
(iv) Rank = 0 if B = 0
OBSERVABILITY
A system is said to be deservable if all the states of the system can be determined on the basis of knowedge
of the o/p of the system at a given time
Kalmans test for observability
2
1
:
n
C
CA
Q CA
CA
(
(
(
(
=
(
(
(
n order of system
Q
0
: observability testing matrix
X AX BV
Y CX DV
= +
= +
(i) System will be completely observable if rank of Q
0
i.e r = n (order system)
(ii) System will be unobservable if rank of Q
0
< n
no of unobservable states = n r
no of observable states = r
r = n if |Q
0
| = 0
Q.3. Determine the state controllability and observability of the system described by
3 1 1 0 1
0 0 1
1 0 1 0 0
1 1 0
0 0 1 2 1
x x u y x
( (
(
( (
= + =
(
( (
( (
Solution :
0 1
0 0
2 1
B
(
(
=
(
(
2
3 1 1 0 1 2 2
1 0 1 0 0 2 0
0 0 1 2 1 2 1
3 1 1 2 2 2 5
1 0 1 2 0 0 3
0 0 1 2 1 0 1
AB
A B
( ( (
( ( (
= =
( ( (
( ( (
( ( (
( ( (
= =
( ( (
( ( (
50
2
[ : : ]
0 1 2 2 2 5
0 0 2 0 0 3
2 1 2 1 2 1
S B AB A B
S
=
(
(
=
(
(
We should be able to collect there colums from s to form a square matrix whose determinant is non-
zero
Let it be
0 1 2
0 0 2
2 1 2
(
(
(
(
and its determinant is
= 0[02 2] 1[20 4] + 2[01 02] = 4
Since the determinant is non-zero the system is controllable and the rank is 3
Observability
3 1 1 3 1 0 0 1
0 0 1
1 0 1 1 0 0 0 1
1 1 0
0 0 1 1 1 1 1 0
3 1 0 0 1 0 4
1 0 0 0 1 0 1
1 1 1 1 0 1 2
T T
T T
A C C A
A C
( ( (
(
( ( (
= = = =
(
( ( (
( ( (
( ( (
( ( (
= =
( ( (
( ( (
3 1 0 0 4 0 11
( ) 1 0 0 0 1 0 4
1 1 1 1 2 1 1
: : ( )
0 1 0 4 0 11
0 1 0 1 0 4
1 0 1 2 1 1
4 0 11
Let us choose 1 0 4
2 1 1
det 4[0 4] 11[1 0] 5
T T T
T T T T T T
A A C
T C A C A A C
( ( (
( ( (
= =
( ( (
( ( (
( =
(
(
=
(
(
(
(
(
(
= + + =
Since determinant is not equal to zero hence rank is 3 and the system is completely observable
Q.4. T.F of a system is given by
3 2
( ) 2
( ) 6 11 6
Y s
U s s s s
=
+ + +
Find controllability and observability
Solution :
1 1
2 2
3 3
0 1 0 0
0 0 1 0
6 11 6 2
x x
x x u
x x
( ( ( (
( ( ( (
= +
( ( ( (
( ( ( (
| |
1
2
3
1 0 0
x
Y x
x
(
(
=
(
(
51
Eigen values are
1 2 3
1 2 3
1 2 3
1 1 1
1, 2, 3
1 1 1 1 1 1
1 2 3
1 4 3
5 1
5 3 1
3
0 1
2 2 2 2
3 4 1 3 4 1 0 2
3 3 2 1 1 1
1 1
2 2 2 2
M
M B M B
= = =
( (
( (
=
( (
( (
(
(
(
( (
(
(
( (
( = = = =
(
( (
(
(
( (
(
(
Since none of rows in matrix B' is zero the system is completely controllable.
Observability
X = CM
| | | |
1 1 1
1 0 0 1 2 3 1 1 1
1 4 9
X
(
(
= =
(
(
Y CM
CMZ
=
=
| |
1
2
3
1 1 1
Z
Z
Z
(
(
=
(
(
The system is completely observable as X = CM = [1, 1, 1] is not having zero element
Q.5. A system is described by the equations
| |
1 1
2 2
3 3
0 1 0 0
0 0 1 0
6 11 6 1
1 1 0
x x
x x u
x x
Y
( ( ( (
( ( ( (
= +
( ( ( (
( ( ( (
=
Find if the system is completely observable if not, find the mode which is not observable.
Solution :
0 1 0
0 0 1
6 11 6
A
(
(
=
(
(
0 0 6 1 1 0
1 0 11 1 1 1
0 1 6 0 0 1
6 1 0 6
( ) 11 1 1 11
5 0 1 5
T T T T T T
T T T
A C A C A C
A A C T
( ( ( (
( ( ( (
= = = =
( ( ( (
( ( ( (
( (
( (
= =
( (
( (
Det (T) = | | 1 (1 5 1 11) (1 11) 0 6(1 0) 0 + =
Since determinant is zero rank is not 3 and hence system is not completely observable.
Eigen values are 1, 2, and 3
52
G (s)
1
R(s)
+
C(s)
+
G (s)
2
+
G (s)
3
G (s)
4
H (s)
2
H (s)
3
H (s)
3
G (s)
1
R(s)
+
C(s) G (s)
2
G (s)
3
G (s)
4
H (s)
1
H (s)
2
+
+
H (s)
3
Y(s)
X(s)
6
5
4
3
2
1
1 2 3 4 5
1 1 1
1 2 3
1 4 9
M
(
(
(
(
| |
| |
1 1 1
1 1 0 1 2 3
1 4 9
0 1 1
X CM
X
(
(
= =
(
(
=
| |
1
2
3
0 1 1
Z
Y CMZ Z
Z
(
(
= =
(
(
Z
1
(t) is not observable a mode due to eigen value = 1
12. PRACTICE SET
Q.1. Determine the transfer function of the system using block diagram reduction of the system shown in
fig.
Q.2. Use block reduction technique obtain the transfer function
(i)
( )
( )
C s
R s
(ii)
( )
( )
C s
X s
(iii)
( )
( )
C s
Y s
(iv) Also find total output
Q.3. Resolve f(t) in terms of step, impulse and ramp functions also find the Laplace transform of f(t)
53
R(s)
+
C(s)
+
G (s)
2
+
G (s)
3
G (s)
4
H (s)
G (s)
2
2
G (s)
1
H (s)
3
H (s)
1
R(s)
+
C(s)
+
G (s)
2
+
G (s)
3
G (s)
4
H (s)
G (s)
2
4
G (s)
1
H (s)
3
H (s)
1
R(s)
+
C(s)
G (s)
3
G (s)
1+G (s)G (s)H (s)+G (s)G (s)H (s)
4
3 4 3 2 3 2
G (s)
1
H (s)
1
R(s)
+
C(s)
+
G (s)
2
G (s)
3
G (s)
1+G (s)G (s)H (s)
4
3 4 3
H (s)
G (s)
2
4
G (s)
1
H (s)
1
Q.4. Find the transfer function of the given of the given circuit shown in fig
(i) (ii)
Q.5. Obtain the transfer function of the given state equation
| |
1 1 1
2 2 2
3 3 3
0 1 0 0
1 1 0 1 0 0 1
1 0 0 0
x x x
x x u Y x
x x x
( ( ( ( (
( ( ( ( (
= + =
( ( ( ( (
( ( ( ( (
Q.6. Obtain the time response of the following system
| |
0 1 0
1. 0
6 5 1
x x u y x
( (
+ =
( (
Where u(t) is a unit step input and initial conditions x
1
(0) = 0 and x
2
(0) = 0
Q.7. The output of a control system is
C(t) = 1 + .25e
50t
1.25e
10t
(i) Obtain the expression for closed loop transfer function of the system
(ii) Determine undamped natural frequency & damping ratio
Assume unit step input
Q.8. The open loop transfer function with unity feedback is
( )
( 2)( 20)
k
G s
s s s
=
+ +
Find analytically the value of k for phase margin = 50
Q.9.
1 1
2 2
.5 0 0
( )
0 2 1
x x
u t
x x
( ( ( (
= +
( ( ( (
| |
1
2
( ) 0 1
x
y t
x
(
=
(
test for controllability and observability
Q.10. The characteristic equation of a feedback control system is s
3
+ 3k s
2
+ (k + 2) s + 4 = 0 determine
the range of k for which system is stable
Q.11. A feedback control system is described as
50 1
( ) ( )
( 2)( 5)
G s H s
s s s s
= =
+ +
For a unit step input, determine the steady state error constants and errors
Solution :(1)
54
R(s)
+
C(s) G(s)
1
H(s)H(s)
1 2
G(s)
2
G(s)
3
G (s)
1
C(s) G (s)
2
G (s)
3
G (s)
4
H (s)
1
H (s)
2
+
X(s)
C(s) G (s)
4
G (s)
3
G (s)G (s)H (s)H (s)
1 2 1 2
+
+
X(s)
G (s)
4
G (s)
1+G (s)G (s)G (s)H (s)H (s)
3
1 2 3 1 2
C(s)
X(s)
1 2 3 4
3 4 3 2 3 2
1 2 3 4 1
( ) ( ) ( ) ( ) ( )
( ) 1 ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
G s G s G s G s C s
R s G s G s H s G s G s H s
G s G s G s G s H s
=
+ +
+
Solution :(2) (i) When R(s) Acting alone and x(s) = 0, Y(s) = 0
1 2 3
1 2 3 1 2
( ) ( ) ( ) ( )
( ) 1 ( ) ( ) ( ) ( ) ( )
G s G s G s C s
R s G s G s G s H s H s
=
+
(ii) When X(s) Acting alone and R(s) = 0 Y(s) = 0
55
G (s)
1
G (s)
2
G (s)
3 C(s)
H (s)
2
H (s)
1
+
H (s)
3
Y(s)
+
C(s) H (s)
3
+
H (s)
1
G (s)G (s)H (s)G (s)
1 2 2 3
Y(s)
C(s)
H (s)
3
G (s)G (s)G (s)
1 2 3
H (s)
1+G (s)G (s)G (s)H (s)H (s)
2
1 2 3 1 2
Y(s)
6
3
2
1
1 2 3 4 5
4s(t3)
3 4
1 2 3 1 2
( ) ( ) ( )
( ) 1 ( ) ( ) ( ) ( ) ( )
G s G s C s
X s G s G s G s H s H s
=
+
(iii) When Y(s) acting alone and R(s) = 0, X(s) = 0
1 2 3 2 3
1 2 3 1 2
( ) ( ) ( ) ( ) ( ) ( )
( ) 1 ( ) ( ) ( ) ( ) ( )
G s G s G s H s H s C s
Y s G s G s G s H s H s
=
+
(iv) total output (i) (iv) (vi)
1 2 3 3 4
1 2 3 2 3
1 2 3 1 2
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
1 ( ) ( ) ( ) ( ) ( )
C s G s G s G s R s G s G s X s
G s G s G s H s H s Y s
G s G s G s H s H s
= +
+
Solution :(3)
1 0 1
4 1 3
( ) 6 3
2 3 4
5 4 5
t
t t
f t t
t
t t
s <
s <
= =
< s
s s
f(t) = | | | | ( ) ( 1) (4 ) ( 1) ( 3) t t t t t +
| |
| |
4 ( 3) 2 4( 3) ( 4)
(5 ) ( 4) ( 5)
s t t t
t u t t
+ +
+
( ) ( ) 2 ( 1) ( 1) ( 1)
( 3) ( 3) ( 3) 4 ( 3)
( 4) ( 4) ( 4) ( 5) ( 5)
f t t t t t
t u t t s t
t u t t t t
= +
+ + +
+
56
I (s)
2
1/cs
E (s)
1
E (s)
1
I (s)
1
E (s)
0
E(s) E (s)
0
I (s)
4
I (s)
3
I (s)
2
1
C s
1 1
I (s)
1
E(s)
i
Z
1 Z
2
Taking the Laplace transform
3 3 4
3 4 5
2
1
( ) 4 1 2
1
s s s s
s s s s
F s e e e e
s
e e e e
s
=
( = + + +
( + + +
Solution (4) (i)
2 2 2
1
2
2
2
( ) ( ) ( ) ( ) ( ) ( )
1 1
1
B A D i i
R R sR c
V s E s V s V s E s E s
sR c
R R
sc sc
= = = =
+
+ +
0 1
1 2 1 2
1 1
0 1
1 1
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
A A
A A
V s E s E s V s
I s I s I s I s
R R
V s E s E s V s
R R
= = =
=
0 0
2
0
2
2 ( ) ( ) ( ) ( ) 2 ( ) ( )
( ) 2 ( ) ( )
1
A i A i
i i
V s E s E s E s V s E s
sR c
E s E s E s
sR c
= + =
(
=
(
+
0 2
2
( ) 1
( ) 1
i
E s scR
E s sR
=
+
1
1
1 1
2 2
1
R
Z
SRC
Z R
=
+
=
V
A
= 0
1 1 1
1
1 1
2
2
( ) ( ) 1
( ) ( )
( )
( )
A
i
E s V s SRC
I s E s
Z R
E s
I s
R
+
= =
=
1 2
( ) ( ) I s I s =
57
( )
2 1 1 2 1 1
1
1 1
0
3 4 3 4
3 4
4
3
0 2 4
1 1
1 3
(1 ) (1 ) ( )
( )
( )
( ) ( )
0 ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( )
(1 )
( )
i
i
B
o o o
i i
i
R SRC R SRC E s
E s E s
R E s R
E s E s
V I s I s I s I s
R R
E s E s E s R E s
E s E s E s E s R
E s R R
SRC
E s R R
+ +
= =
= = = =
= =
= +
Solution (5)
| |
| |
3
2
2
2
0 1 0 0
1 1 0 , 1 0 0 1
1 0 0 0
1 0
1 1 0 1
1 0
0
( ) 0
1 1 1
T
A B C
s
SI A s SI A s s
s
s s s
Adj SI A s s
s s s
( (
( (
= = =
( (
( (
(
(
= + = + +
(
(
( +
(
=
(
(
+ + +
| |
1 ( )
| |
Adj SI A
SI A
SI A
=
| |
2 2
2 2
2 2
2 2
1
2 2 3 2
2 2
1 1
0
1 1
1
0
1 1
1 1 1
( 1) ( 1)
1 1
0
1 1
0
1 1
[ ] 0 0 1 0 1
1 1 1
0
1 1 1
( 1) ( 1)
T
s
s s s s
s
s s s s
s
s s s s s s s
s
s s s s
s
C SI A B
s s s s s s
s
s s s s s s s
( +
(
+ + + +
(
(
=
(
+ + + +
(
+
(
(
+ + + +
( +
(
+ + + +
( (
( (
= =
( (
+ + + + + +
( (
+
(
(
+ + + +
Solution (6)
0 1 0
6 5 1
A B
( (
= =
( (
58
2
1
1
0 0 1 1
0 6 5 6 5
5 6 ( 2)( 3)
5 6
( )
1 5
5 1
( )
6 5
5 1
( 2)( 3) ( 2)( 3)
[ ]
6
( 2)( 3) ( 2)( 3)
3
[ ]
s s
SI A
s s
SI A s s s s
s
Cofactors of SI A
s
Adj of SI A
s
s s s s
SI A
s
s s s s
s
SI A
( ( (
= =
( ( (
+
= + + = + +
+ (
=
(
+ (
=
(
+ (
(
+ + + +
(
=
(
(
+ + + +
=
2 3 2 3
1 1
2 3 2 3
( )
0
2 1 1
2 3 2 3
6 6 2 3
2 3 2 3
3 2
[ ]
6 6 2 3
( ) (0) ( )
t t t t
t t t t
t
At A t
s s s
s s s s
e e e e
L SI A
e e e e
x t e x e B d
t
t t
(
(
+ + + +
(
(
+ +
(
+ + + +
(
=
(
+ +
= +
}
2 3 2 3
2 3 2 3
2( ) 2( ) 3( )
2( ) 3( ) 2( ) 3( )
0
0 3 2
( )
0 6 6 2 3
0 3 3( )
1
1 6 6 2 3
t t t t
t t t t
t t t t
t t t t
e e e e
x t
e e e e
e t e e
d
e e e e
t t t
t t t t
t
t
+
( (
=
( (
+ +
( (
+
( (
+ +
}
2( ) 3( )
2( ) 3( )
0
( )
2 3
t t t
t t
e e
x t d
e e
t t
t t
t
=
`
+
)
}
{ }
2( ) 3( )
1
0
0
3 2( ) 2
3 0
2 3 2 3
1 2
( )
3( ) , 0, 3
1
, , 0
3
1 1 1 1 1
3 3 3 2 2
1 1 1
( ) ( )
6 2 3
t
t t
t
x t t t
t
t t t t
x t e e d
t x x t
d dx t x
e dx e e d e
x t e e x t e e
t t
t
t
t t
t t
t
=
= = =
= = =
= =
= =
}
} }
Solution (7) (i) C(t) = 1 + .25 e
sot
1.25e
10t
1 .25 1.2 500
. . ( )
50 10 ( 50)( 10)
1 ( ) 500
( )
( ) ( 50)( 10)
s
LT C s
s s s s s s
C s
R s
s R s s s
= + =
+ + + +
= =
+ +
59
(ii)
2
( ) 500
( ) 60 500
C s
R s s s
=
+ +
2
500, 22.36 2 60 1.34
n n n
e e ce c = = = =
Solution (8) ( ) ( )
( 2)( 20)
k
G s H s
s s s
=
+ +
=
/ 40
(1 .5 )(1 .05 )
k
j j j e e e + +
PM = 180 + ( ) ( ) G j H j e e
1 1
1 1
1 1
1 1
2
( ) ( ) 90 tan . tan .0
0 180 ( 90 tan . tan .0 )
40 tan . tan .0
tan 40 tan(tan . tan .0 )
.5
.839
1 .025
G j H j s s
S S S
s S
S S
S
e e e e
e e
e e
e e
e
e
=
= +
= +
= +
=
1.445 / sec rad e =
The is the gain cross-over frequency e
g
= 1.445 r/sec at gain cross over frequency
( ) ( ) 1
40
1
1.44 1 .722 1 .0722
1.7873 71.49
40
G j H j
k
j s j s j s
k
k
e e =
=
+ +
= =
Solution (9) Q = [B : AB]
.5 0 0
,
0 2 1
A B
( (
= =
( (
0 0 0
,
2 1 2
AB Q
( (
= =
( (
Rank of Q is one hence system is uncontrollable
| |
0
0 1 ,
1
. 0 0
,
0 2 2
0 0
' : '
1 2
T
T T T
T T T
C C
s
A A C
Q C A C Q
(
= =
(
( (
= =
( (
(
( = =
(
Rank of Q is one hence the system is unobservable for controllability and observability the rank
should be two
The given system is uncontrollable and unobservable
Solution :(10) Rouths array is
S
3
1 k + 2
S
2
3k 4
S
1
2
3 6 4
3
k k
k
+
S
0
4
60
3k > 0, 3k
2
+ 6k 4 > 0
k > 1 1.53 k > .53
the range of k is thus
> k > .53
Solution (11)
2
2
0 0
0
2
0 0
50
( ) ( )
( 2)( 5)
50
lim ( ) ( ) lim
( 2)( 5)
lim ( ) ( )
50
lim ( ) ( ) lim 5
( 2)( 5)
p p
s s
v
s
a
s s
G s H s
s s s
k G s H s k
s s s
k sG s H s
k s G s H s
s s
=
+ +
= = =
+ +
= =
= = =
+ +
steady state error =
0
( )
lim
1 ( ) ( )
s
sR s
G s H s
+
1
( ) R s
s
= therefore
2
4 3 2
0
( 2)( 5)
lim
7 10 50
0
s
s s s
s s s
+ +
=
+ + +
=
S-ar putea să vă placă și
- Control SystemDocument16 paginiControl Systemmsm158Încă nu există evaluări
- Control System PresentationDocument10 paginiControl System PresentationVikneshwaran Keluan SinghÎncă nu există evaluări
- Fan Selection Guide PDFDocument16 paginiFan Selection Guide PDFHarsh KhatriÎncă nu există evaluări
- Application of Ponding Systems in The Treatment ofDocument10 paginiApplication of Ponding Systems in The Treatment ofbenjiy80Încă nu există evaluări
- 03a. Industrial Control SystemsDocument25 pagini03a. Industrial Control SystemsKhaled KamalÎncă nu există evaluări
- Reduction of High Maintenance Costs by Noah Olela Abong'oDocument20 paginiReduction of High Maintenance Costs by Noah Olela Abong'oNABONGO2Încă nu există evaluări
- Basic Electrical TheoryDocument13 paginiBasic Electrical Theoryapi-628245069Încă nu există evaluări
- Screw Conveyor O&M ManualDocument20 paginiScrew Conveyor O&M Manualjay b100% (1)
- PID controller explainedDocument22 paginiPID controller explainedmansoorÎncă nu există evaluări
- Surface Water Treatment Process A Review On Variou PDFDocument10 paginiSurface Water Treatment Process A Review On Variou PDFWilda Safira RahmaniaÎncă nu există evaluări
- Control System PresentationDocument15 paginiControl System PresentationecegianÎncă nu există evaluări
- Fan Bearing Selection Fe 1200Document4 paginiFan Bearing Selection Fe 1200phineasphineÎncă nu există evaluări
- Palm Oil Mills Targets Zero EmissionDocument5 paginiPalm Oil Mills Targets Zero EmissionscreenscreamerÎncă nu există evaluări
- Centrifuge Preventative Maintenance Schedule: EBA 20, EBA 20S, MIKRO 120 See Lower Chart Centrifuge Bowl SealDocument1 paginăCentrifuge Preventative Maintenance Schedule: EBA 20, EBA 20S, MIKRO 120 See Lower Chart Centrifuge Bowl SealSubbarayan SaravanakumarÎncă nu există evaluări
- Waste MGMT & Env ControlDocument45 paginiWaste MGMT & Env ControlMasrawana Mohd Masran100% (1)
- StorkReview PDFDocument128 paginiStorkReview PDFuma shankar balakrishnanÎncă nu există evaluări
- Richards Bay Minerals: General RBM ProcedureDocument7 paginiRichards Bay Minerals: General RBM ProcedureHuzaifa KtkÎncă nu există evaluări
- Power PlantDocument24 paginiPower PlantARUNGREESMAÎncă nu există evaluări
- Baling Machine-Myway 10TDocument1 paginăBaling Machine-Myway 10TPt eyd Technic indonesiaÎncă nu există evaluări
- Fluid Mechanics NotesDocument12 paginiFluid Mechanics Notessubha_aeroÎncă nu există evaluări
- 9780470209677.chap 10 ProblemsDocument3 pagini9780470209677.chap 10 ProblemsAnonymous yF1z4oÎncă nu există evaluări
- Mechatronics Application and System DesignDocument10 paginiMechatronics Application and System Designswap1983Încă nu există evaluări
- Poeb130 YosriDocument9 paginiPoeb130 YosriNa'imusyahmi Ghazali100% (1)
- Desiccated CoconutDocument38 paginiDesiccated CoconutPrecious BautistaÎncă nu există evaluări
- Soya Lecithin PlantDocument3 paginiSoya Lecithin PlantM Mohsin ChowdhuryÎncă nu există evaluări
- Training & Development 270615 - 1462621623597Document98 paginiTraining & Development 270615 - 1462621623597Pavani Meher0% (1)
- 10 Boiler Ash Removal System Commissioning Procedure-TöàtéëTÖñtü T +T+ƑF Âf Ò Ä Û+Document32 pagini10 Boiler Ash Removal System Commissioning Procedure-TöàtéëTÖñtü T +T+ƑF Âf Ò Ä Û+kvsagar100% (1)
- OzonationDocument4 paginiOzonationKareen Jenn AmlosÎncă nu există evaluări
- Engineered Systems For Air Pollution ControlDocument17 paginiEngineered Systems For Air Pollution ControlnikhilÎncă nu există evaluări
- Boiler Flow DiagramDocument1 paginăBoiler Flow Diagramshobhan1984Încă nu există evaluări
- Modelling and Simulation of Industrial ProcessesDocument1 paginăModelling and Simulation of Industrial ProcessesCésar SandovalÎncă nu există evaluări
- Applied Hydraulics and Pneumatics 2 Mark QuestionsDocument5 paginiApplied Hydraulics and Pneumatics 2 Mark QuestionsChandni DayakarÎncă nu există evaluări
- Scope of Irrigation EngineeringDocument12 paginiScope of Irrigation EngineeringDeepjyoti Kalita100% (1)
- 2.5 Insulation & Refractories - Revised (Table Format)Document9 pagini2.5 Insulation & Refractories - Revised (Table Format)Sachith Praminda Rupasinghe100% (1)
- Mechanical Maintenance Palm Mill OilDocument38 paginiMechanical Maintenance Palm Mill Oilvicky alviolandÎncă nu există evaluări
- Semi-Automated Paddy ThresherDocument26 paginiSemi-Automated Paddy Thresherksati311Încă nu există evaluări
- Biogas Capture From Palm Oil Mill Effluent For Power Generation On 27.3.2014 (For MR CHIN)Document13 paginiBiogas Capture From Palm Oil Mill Effluent For Power Generation On 27.3.2014 (For MR CHIN)Wan Zahir100% (1)
- Vacuum deaerator reduces corrosionDocument2 paginiVacuum deaerator reduces corrosionGaurav100% (1)
- Eme Lab Manual PDFDocument45 paginiEme Lab Manual PDFpatidar montuÎncă nu există evaluări
- A General Review of Palm Oil Mill EffluentDocument3 paginiA General Review of Palm Oil Mill EffluentMykel-Deitrick Boafo DuoduÎncă nu există evaluări
- Final Proposal Etp ExampleDocument11 paginiFinal Proposal Etp ExampleAfif IzwanÎncă nu există evaluări
- Nonlinear Predictive Control For The Four-Tanks Plant Flow RegulationDocument6 paginiNonlinear Predictive Control For The Four-Tanks Plant Flow RegulationPhạm Ngọc HuyÎncă nu există evaluări
- Remove gases from boiler feedwater with deaerationDocument5 paginiRemove gases from boiler feedwater with deaerationGovindarajan ChandrasekaranÎncă nu există evaluări
- SKF GreaseDocument3 paginiSKF GreaseKumar SwamiÎncă nu există evaluări
- Troubleshooting Screw ConveyorDocument5 paginiTroubleshooting Screw ConveyorFran JimenezÎncă nu există evaluări
- Assignment 1Document4 paginiAssignment 1Ziyad Awali100% (1)
- Project DescriptionDocument32 paginiProject Descriptionxiangjintao50% (2)
- Forced Circulation EvaporatorsDocument11 paginiForced Circulation EvaporatorsFurqan MughalÎncă nu există evaluări
- 2.2 POM Upgrading - Part 1Document17 pagini2.2 POM Upgrading - Part 1Buditama ChandranegaraÎncă nu există evaluări
- Control & Inst - V-IDocument180 paginiControl & Inst - V-ISiva Kumar TutikaÎncă nu există evaluări
- Exergy Analysis of Organic Rankine CycleDocument9 paginiExergy Analysis of Organic Rankine CycleMukul GoyalÎncă nu există evaluări
- NonMinimum Phase Control SystemsDocument5 paginiNonMinimum Phase Control SystemsD.ViswanathÎncă nu există evaluări
- First Resources Limited Delivering Growth and ReturnsDocument35 paginiFirst Resources Limited Delivering Growth and ReturnsrizkydjonhansemitÎncă nu există evaluări
- Unit 3 Cleaning and Grading: StructureDocument21 paginiUnit 3 Cleaning and Grading: StructureMoonsoul ChildÎncă nu există evaluări
- Dorner 3200 Vacuum ConveyorDocument8 paginiDorner 3200 Vacuum ConveyorBobKatÎncă nu există evaluări
- Chapter 4 TurbineDocument56 paginiChapter 4 TurbineHabtamu Tkubet EbuyÎncă nu există evaluări
- MECHATRONICS MODULE II SYLLABUSDocument65 paginiMECHATRONICS MODULE II SYLLABUSNazeema TTÎncă nu există evaluări
- ME2142 Tut 2 SolnDocument8 paginiME2142 Tut 2 SolnLakshmi Balasubramaniam100% (1)
- Midterm 12 SolDocument5 paginiMidterm 12 SolShinee JayasilanÎncă nu există evaluări
- Control Systems Formula SheetDocument12 paginiControl Systems Formula SheetliamhrÎncă nu există evaluări
- 5.ramp Response of A Transfer FunctionDocument5 pagini5.ramp Response of A Transfer FunctionNishant SaxenaÎncă nu există evaluări
- 4.impulse Response of A Transfer FunctionDocument4 pagini4.impulse Response of A Transfer FunctionNishant SaxenaÎncă nu există evaluări
- Transmission and Distribution of Electrical PowerDocument53 paginiTransmission and Distribution of Electrical PowerNishant SaxenaÎncă nu există evaluări
- Gyan Vihar School engineering dept presentation reportsDocument1 paginăGyan Vihar School engineering dept presentation reportsNishant SaxenaÎncă nu există evaluări
- Engineer in Tranmission PDFDocument5 paginiEngineer in Tranmission PDFNishant SaxenaÎncă nu există evaluări
- Control SystemDocument38 paginiControl SystemNishant SaxenaÎncă nu există evaluări
- MCQ On MATLABDocument17 paginiMCQ On MATLABNishant Saxena75% (4)
- Quality Checklist For Online Modules (Qcom)Document2 paginiQuality Checklist For Online Modules (Qcom)Nishant SaxenaÎncă nu există evaluări
- Format For Faculty Subject Changement On LMS EEDocument2 paginiFormat For Faculty Subject Changement On LMS EENishant SaxenaÎncă nu există evaluări
- Voltage and Current Transfer Ratios in Electrical CircuitsDocument43 paginiVoltage and Current Transfer Ratios in Electrical CircuitsNishant Saxena100% (1)
- Electrical Engineering: KCT College of Engg and Tech. Village Fatehgarh Distt - SangrurDocument23 paginiElectrical Engineering: KCT College of Engg and Tech. Village Fatehgarh Distt - SangrurNishant SaxenaÎncă nu există evaluări
- Notice - CAT NO. NW10416, NW10516, NW11516, NW11716Document1 paginăNotice - CAT NO. NW10416, NW10516, NW11516, NW11716Nishant SaxenaÎncă nu există evaluări
- Analog ElectronicsDocument34 paginiAnalog ElectronicsNishant Saxena100% (1)
- Reactive Power Dispatch Using Big Bang-Big CrunchDocument6 paginiReactive Power Dispatch Using Big Bang-Big CrunchNishant SaxenaÎncă nu există evaluări
- VHDL MCQDocument35 paginiVHDL MCQNishant Saxena100% (2)
- GATE Quation Paper - 2015 PDFDocument15 paginiGATE Quation Paper - 2015 PDFAnonymous tT4RaNCiÎncă nu există evaluări
- Mathematical Modelling of Sampling ProcessDocument6 paginiMathematical Modelling of Sampling ProcessNishant SaxenaÎncă nu există evaluări
- EEgate 16Document28 paginiEEgate 16Rajesh KumarÎncă nu există evaluări
- Ac Machine MannualDocument6 paginiAc Machine MannualNishant SaxenaÎncă nu există evaluări
- Lab Mannual Ac 1Document5 paginiLab Mannual Ac 1Nishant SaxenaÎncă nu există evaluări
- Modern and Digital Control EngineeringDocument1 paginăModern and Digital Control EngineeringNishant SaxenaÎncă nu există evaluări
- L-14 (SS) (Iac) ( (Ee) Nptel)Document10 paginiL-14 (SS) (Iac) ( (Ee) Nptel)Marvin BayanayÎncă nu există evaluări
- Course Handout MC1Document5 paginiCourse Handout MC1Nishant SaxenaÎncă nu există evaluări
- Electronics and CommunicationDocument200 paginiElectronics and CommunicationNishant SaxenaÎncă nu există evaluări
- 4 Semester, EEE Electrical Machine 1Document16 pagini4 Semester, EEE Electrical Machine 1Nishant SaxenaÎncă nu există evaluări
- Course Handout UEEDocument5 paginiCourse Handout UEENishant SaxenaÎncă nu există evaluări
- Course Handout PPEDocument4 paginiCourse Handout PPENishant SaxenaÎncă nu există evaluări
- Course Handout PS IDocument4 paginiCourse Handout PS INishant SaxenaÎncă nu există evaluări
- Course Handout PSIIDocument4 paginiCourse Handout PSIINishant SaxenaÎncă nu există evaluări
- Amity University Rajasthan Core Electrical Subjects by SemesterDocument1 paginăAmity University Rajasthan Core Electrical Subjects by SemesterNishant SaxenaÎncă nu există evaluări
- Scaling Laws For Neural Language ModelsDocument30 paginiScaling Laws For Neural Language ModelsMarcos CostaÎncă nu există evaluări
- EC2202-question BankDocument24 paginiEC2202-question BankAnirudhan RaviÎncă nu există evaluări
- Mathematical Foundations for Data ScienceDocument29 paginiMathematical Foundations for Data ScienceManisha MÎncă nu există evaluări
- ECO686 Slides 5Document25 paginiECO686 Slides 5samiyah.haque01Încă nu există evaluări
- Convolutional neural networks for text classification: Implementing forward, backward and gradient checkingDocument3 paginiConvolutional neural networks for text classification: Implementing forward, backward and gradient checkingYvonne Yifan ZhouÎncă nu există evaluări
- 1 (I) - Unbounded - Since There Is No Single Poiny in Feasible Region That Can Maximize The FunctionDocument5 pagini1 (I) - Unbounded - Since There Is No Single Poiny in Feasible Region That Can Maximize The FunctionPolu Vidya SagarÎncă nu există evaluări
- Questions IE621Document10 paginiQuestions IE621KushÎncă nu există evaluări
- DS LAB-3 Rahul Singh (191B317)Document7 paginiDS LAB-3 Rahul Singh (191B317)Rahul Singh100% (1)
- A Comparison of Different Automated Market-Maker StrategiesDocument14 paginiA Comparison of Different Automated Market-Maker StrategiesmeamaÎncă nu există evaluări
- Factors Affecting Career Choices of Grade 12 StudentsDocument6 paginiFactors Affecting Career Choices of Grade 12 StudentsJenneth Cabinto DalisanÎncă nu există evaluări
- Coding Ninjas Bootcamp Curriculum-26523Document28 paginiCoding Ninjas Bootcamp Curriculum-26523Manjeet SharmaÎncă nu există evaluări
- 04 Using Block v2 AnnotatedDocument54 pagini04 Using Block v2 AnnotatedbodokidÎncă nu există evaluări
- Stat Proof BookDocument381 paginiStat Proof BookAdam SmithÎncă nu există evaluări
- Voice RecognitionDocument6 paginiVoice RecognitionVuong LuongÎncă nu există evaluări
- 2 Network Modeling-The Admittance Model PSA NUST Postgraduate Fall 2022Document33 pagini2 Network Modeling-The Admittance Model PSA NUST Postgraduate Fall 2022Owais JafriÎncă nu există evaluări
- CS502 Finl Term Hndsout by Dream TeamDocument88 paginiCS502 Finl Term Hndsout by Dream Teamfakhira siddiqÎncă nu există evaluări
- Dwnload Full Data Abstraction and Problem Solving With C Walls and Mirrors 7th Edition Carrano Solutions Manual PDFDocument36 paginiDwnload Full Data Abstraction and Problem Solving With C Walls and Mirrors 7th Edition Carrano Solutions Manual PDFlesliepooleutss100% (14)
- Stream Ciphers: Cryptography - CS 507 Erkay Savas Sabancı UniversityDocument37 paginiStream Ciphers: Cryptography - CS 507 Erkay Savas Sabancı UniversitymasterofdonÎncă nu există evaluări
- DAA Course File III Year II SEMDocument17 paginiDAA Course File III Year II SEMXyz 1234SBCÎncă nu există evaluări
- Assignment 1Document8 paginiAssignment 1Alex HarrisÎncă nu există evaluări
- Lesson 3.1 One To OneDocument25 paginiLesson 3.1 One To OneMaricris OcampoÎncă nu există evaluări
- Cs205-E S3dec18 KtuwebDocument2 paginiCs205-E S3dec18 KtuwebVighnesh MuralyÎncă nu există evaluări
- Chapter15 Key ManagementDocument19 paginiChapter15 Key ManagementtartarÎncă nu există evaluări
- Machine Learning Paper ReviewDocument17 paginiMachine Learning Paper ReviewAnkit RamÎncă nu există evaluări
- 6450 Bayesian Final Project Report - Team 2Document15 pagini6450 Bayesian Final Project Report - Team 2Ali iÎncă nu există evaluări
- Rook PivotingDocument12 paginiRook PivotingelomaniparoÎncă nu există evaluări
- 2023 Oct CSC649 Group Project - Evaluation FormDocument1 pagină2023 Oct CSC649 Group Project - Evaluation FormMUHAMMAD AMER FAIZ BIN ABDUL RAHMANÎncă nu există evaluări
- OptimizacionDocument296 paginiOptimizacionMaiÎncă nu există evaluări
- Sliding Mode ControlDocument12 paginiSliding Mode ControlakhilvjÎncă nu există evaluări
- Machine Learning Engineer Nanodegree: Capstone ProposalDocument3 paginiMachine Learning Engineer Nanodegree: Capstone ProposalKhalil HenchiÎncă nu există evaluări