Documente Academic
Documente Profesional
Documente Cultură
Lesson 12.4
Încărcat de
lestianaTitlu original
Drepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
Lesson 12.4
Încărcat de
lestianaDrepturi de autor:
Formate disponibile
Lesson
Page 1 of 6
L E S S O N
12.4
A ship in a port is safe,
but that is not what
ships are built for.
JOHN A. SHEDD
keymath.com/DG
The Law of Cosines
Youve solved a variety of problems with the Pythagorean Theorem. It is perhaps
your most important geometry conjecture. In Chapter 9, you found that the
distance formula is really just the Pythagorean Theorem. You even used the
Pythagorean Theorem to derive the equation of a circle.
The Pythagorean Theorem is very powerful, but its use is still limited to right
triangles. Recall from Chapter 9 that the Pythagorean Theorem does not work for
acute triangles or obtuse triangles. You might ask, What happens to the
Pythagorean equation for acute triangles or obtuse triangles?
For an interactive version of this sketch, see the Dynamic Geometry Exploration
The Law of Cosines at www.keymath.com/DG .
If the legs of a right triangle are brought closer together so that the right angle
becomes an acute angle, youll find that c2 < a2 + b2. In order to make this
inequality into an equality, you would have to subtract something from a2 + b2.
c2 = a2 + b2 something
If the legs are widened to form an obtuse angle, youll find that c2 > a2 + b2.
Here, youd have to add something to make an equality.
c2 = a2 + b2 + something
Mathematicians found that the something was 2ab cos C. The Pythagorean
Theorem generalizes to all triangles with a property called the Law of Cosines.
Law of Cosines
For any triangle with sides of lengths a, b,and c,and with C the angle
opposite the side with length c,
c2 = a2 + b2 2ab cos C
For obtuse angles, the expression 2ab cos C is negative, so subtracting it adds a
positive quantity. Trigonometric ratios for angles larger than 90 are introduced in
the Exploration Trigonometric Ratios and the Unit Circle.
2008 Key Curriculum Press
http://acr.keypress.com/KeyPressPortalV3.0/Viewer/Lesson.htm
LESSON 12.4 The Law of Cosines
661
2/25/2009
Lesson
Page 2 of 6
To derive the Law of Cosines for an acute
triangle, consider acute ABC with
altitude AD , as shown at right. You can
define the lengths of the sides opposite
angles A, B,and C as a, b,and c,
respectively, the height as h, and the
length of CD as x. The length of BD is
the difference between the lengths of BC
and CD ,or a x.
Using the Pythagorean Theorem, you can write two equations. By algebra, you can
expand (a x)2.
x2 + h2 = b2
(a x)2 + h2 = c2
a2 2ax + x2 + h2 = c2
Notice that this new equation contains x2 + h2, which you know is equal to b2 from
the first equation. Substitute, rearrange the terms, and reverse the equation.
a2 2ax + b2 = c2
a2 + b2 2ax = c2
c2 = a2 + b2 2ax
Now you need to replace x with an expression containing the cosine of C. Using
ACD, you can write the following equation and then solve for x.
cos C
b cos C = x
Substituting this expression for x into the equation above results in the Law
of Cosines.
c2 = a2 + b2 2abcos C
While this derivation of the Law of Cosines is for an acute triangle, it also works
for obtuse triangles. Deriving the Law of Cosines for an obtuse triangle is left as a
Take Another Look activity.
You can use the Law of Cosines when you are given three side lengths or two side
lengths and the angle measure between them (SSS or SAS).
EXAMPLE A
Solution
Find the length of side CT in triangle CRT.
To find r, use the Law of Cosines:
c2 = a2 + b2 2ab cos C
662
The Law of Cosines.
CHAPTER 12 Trigonometry
http://acr.keypress.com/KeyPressPortalV3.0/Viewer/Lesson.htm
2008 Key Curriculum Press
2/25/2009
Lesson
Page 3 of 6
Using the variables in this problem, the Law of Cosines becomes
r2 = c2 + t2 2ct cos R
Substitute r for c, c for a, t for b,and R for C
r2 = 452 + 522 2(45)(52)(cos 36)
Substitute 45 for c,52 for t,and 36 for R .
r
r
Take the positive square root of both sides.
31
Evaluate.
The length of side CT is about 31 cm.
EXAMPLE B
Solution
Find the measure of
Q in triangle QED.
Use the Law of Cosines and solve for Q.
q2 = e2 + d2 2ed cos Q
The Law of Cosines with respect to
cos Q
Solve for cos Q.
cos Q
Substitute known values.
Q
Q
Q.
Take the inverse cosine of both sides.
76
The measure of
Evaluate.
Q is about 76.
You will need
EXERCISES
In Exercises 13, find each length to the nearest centimeter.
1. w
2. y
2008 Key Curriculum Press
http://acr.keypress.com/KeyPressPortalV3.0/Viewer/Lesson.htm
3. x
LESSON 12.4 The Law of Cosines
663
2/25/2009
Lesson
Page 4 of 6
In Exercises 46, each triangle is an acute triangle. Find each angle measure to the
nearest degree.
4. m A
5. m B
6. m C
7. Two 24-centimeter radii of a circle form a central angle measuring 126. What is the
length of the chord connecting the two radii?
8. Find the measure of the smallest angle in a triangle whose side lengths are 4 m, 7 m,
and 8 m.
9. Two sides of a parallelogram measure 15 cm and 20 cm, and one of the diagonals
measures 19 cm. What are the measures of the angles of the parallelogram to the
nearest degree?
10. Application Captain Malloy is flying a
passenger jet. He is heading east at 720 km/h
when he sees an electrical storm straight
ahead. He turns the jet 20 to the north to
avoid the storm and continues in this direction
for 1 h. Then he makes a second turn, back
toward his original flight path. Eighty minutes
after his second turn, he makes a third turn
and is back on course. By avoiding the storm,
how much time did Captain Malloy lose from
his original flight plan?
Review
11. Application A cargo company loads truck
trailers into ship cargo containers. The trucks
drive up a ramp to a horizontal loading
platform 30 ft off the ground, but they have
difficulty driving up a ramp at an angle
steeper than 20. What is the minimum length
that the ramp needs to be?
12. Application Dakota Davis uncovers the remains
of a square-based Egyptian pyramid. The base
is intact and measures 130 meters on each side. The top of the pyramid has
eroded away, but what remains of each face of the pyramid forms a 65 angle
with the ground. What was the original height of the pyramid?
664
CHAPTER 12 Trigonometry
http://acr.keypress.com/KeyPressPortalV3.0/Viewer/Lesson.htm
2008 Key Curriculum Press
2/25/2009
Lesson
Page 5 of 6
13. Application A lighthouse 55 meters above sea level spots a distress signal from a
sailboat. The angle of depression to the sailboat measures 21. How far away is the
sailboat from the base of the lighthouse?
14. Application A painting company has a general safety rule to place ladders at an angle
measuring between 55 and 75 from the level ground. Regina places the foot of her
25 ft ladder 6 ft from the base of a wall. What is the angle of the ladder? Is the ladder
placed safely? If not, how far from the base of the wall should she place the ladder?
15. Show that
tan A.
16. TRAP is an isosceles trapezoid.
a. Find PR in terms of x.
b. Write a paragraph proof to show that
m TPR = 90.
17. As P moves to the right on line
happens to
a. m ABP
b. m PAB
c. m APB
, describe what
18. Which of these figures, the cone or the square
pyramid, has the greater
a. Base perimeter?
b. Volume?
c. Surface area?
19. What single transformation is equivalent to the composition of each pair of
functions? Write a rule for each.
a. A reflection over the line x = 2 followed by a reflection over the line x = 3
b. A reflection over the x-axis followed by a reflection over the y-axis
20. Construction Construct two rectangles that are not similar.
21. Construction Construct two isosceles trapezoids that are similar.
22. Technology Use geometry software to construct two
circles. Connect the circles with a segment and
construct the midpoint of the segment. Animate
the endpoints of the segment around the circles
and trace the midpoint of the segment. What shape
does the midpoint of the segment trace? Try
adjusting the relative size of the radii of the circles;
try changing the distance between the centers of
the circles; try starting the endpoints of the
segment in different positions; or try animating the
endpoints of the segment in different directions. Describe how these changes affect
the shape traced by the midpoint of the segment.
2008 Key Curriculum Press
http://acr.keypress.com/KeyPressPortalV3.0/Viewer/Lesson.htm
LESSON 12.4 The Law of Cosines
665
2/25/2009
Lesson
Page 6 of 6
JAPANESE TEMPLE TABLETS
For centuries it has been customary in Japan to hang colorful wooden tablets in Shinto
shrines to honor the gods of this native religion. During Japans historical period of
isolation (16391854), this tradition continued with a mathematical twist. Merchants,
farmers, and others who were dedicated to mathematical learning made tablets
containing mathematical problems,called sangaku, to inspire and challenge visitors.
See if you can answer this sangaku problem.
These circles are tangent to each other and to the line.
How are the radii of the three circles related?
Research other sangaku problems, then design your own
tablet. Your project should include
Your solution to the problem above.
Some problems you found during your research and your sources.
Your own decorated sangaku tablet with its solution on the back.
666
CHAPTER 12 Trigonometry
http://acr.keypress.com/KeyPressPortalV3.0/Viewer/Lesson.htm
2008 Key Curriculum Press
2/25/2009
S-ar putea să vă placă și
- Chapter 9 TrigonometryDocument52 paginiChapter 9 TrigonometryJojobaby51714100% (3)
- Pusheen With Donut: Light Grey, Dark Grey, Brown, RoséDocument13 paginiPusheen With Donut: Light Grey, Dark Grey, Brown, RosémafaldasÎncă nu există evaluări
- 5 Right TriangleDocument15 pagini5 Right TriangleNeal John VillarmenteÎncă nu există evaluări
- Law of Cosines WorksheetDocument8 paginiLaw of Cosines WorksheetKhyllSanecaÎncă nu există evaluări
- Trigonometry: What You Will LearnDocument44 paginiTrigonometry: What You Will LearnJimmy Ieng100% (2)
- Vanish Magic Magazine VANISH MAGIC MAGAZINE 58 May 2019Document118 paginiVanish Magic Magazine VANISH MAGIC MAGAZINE 58 May 2019mick byrnes100% (1)
- The Surprise Attack in Mathematical ProblemsDe la EverandThe Surprise Attack in Mathematical ProblemsEvaluare: 4 din 5 stele4/5 (1)
- Critical Analysis of W.H Auden Poems The PDFDocument8 paginiCritical Analysis of W.H Auden Poems The PDFMöĤämmĔd äĹ-ŚäÁdï100% (1)
- Terminals of Ecm: E3 E4 E5 E6Document2 paginiTerminals of Ecm: E3 E4 E5 E6jeremih alhegn100% (1)
- MathsTraks: Geometry: A Collection of Blackline Masters for ages 11-14De la EverandMathsTraks: Geometry: A Collection of Blackline Masters for ages 11-14Încă nu există evaluări
- 11 3 Angles of Elevation and DepressionDocument27 pagini11 3 Angles of Elevation and DepressiongiyagirlsÎncă nu există evaluări
- Multi Pressure Refrigeration CyclesDocument41 paginiMulti Pressure Refrigeration CyclesSyed Wajih Ul Hassan80% (10)
- Math 9 ModuleDocument25 paginiMath 9 Modulewetlog lolololimÎncă nu există evaluări
- Practice Aime GeometryDocument3 paginiPractice Aime Geometryสฮาบูดีน สาและÎncă nu există evaluări
- Mathematics 9 - Q3 - Mod5 - Proving Theorems On The Different Kinds of Parallelogram - V3Document17 paginiMathematics 9 - Q3 - Mod5 - Proving Theorems On The Different Kinds of Parallelogram - V3alexablisss100% (1)
- Maritime Management SystemsDocument105 paginiMaritime Management SystemsAndika AntakaÎncă nu există evaluări
- IGCSE Resources - Physics Sample Papers (For 2023 Syllabus) - V2Document44 paginiIGCSE Resources - Physics Sample Papers (For 2023 Syllabus) - V2Emma Isabella GraceÎncă nu există evaluări
- Worksheet With Answer KeyDocument8 paginiWorksheet With Answer Keyapi-213604106Încă nu există evaluări
- Precalculus Functions and Graphs 13th Edition Swokowski Test BankDocument5 paginiPrecalculus Functions and Graphs 13th Edition Swokowski Test Bankotiseirianpjsd100% (19)
- Notes - Law of Sines and CosinesDocument8 paginiNotes - Law of Sines and CosinesLong NguyễnÎncă nu există evaluări
- 5 - Q4 MathDocument26 pagini5 - Q4 Mathmaximo meridaÎncă nu există evaluări
- CE 3220 Quiz 1 2nd Sem S.Y. 2021 2022 - 1 - 1Document2 paginiCE 3220 Quiz 1 2nd Sem S.Y. 2021 2022 - 1 - 1JasÎncă nu există evaluări
- Prelims Math 2Document4 paginiPrelims Math 2Ramon Jr. MontesorÎncă nu există evaluări
- HangmanDocument3 paginiHangmanTendai MatomaÎncă nu există evaluări
- TrigonometryDocument4 paginiTrigonometrydayatÎncă nu există evaluări
- Math 9 q3 Module 1Document26 paginiMath 9 q3 Module 1Rowell C GravaÎncă nu există evaluări
- 4th Quarter Math 9Document3 pagini4th Quarter Math 9Mark Joseph VelascoÎncă nu există evaluări
- Oblique TrianglesDocument27 paginiOblique TrianglesJerome SagunÎncă nu există evaluări
- Math 9Document5 paginiMath 9Absy BunsayÎncă nu există evaluări
- Mathematics of Flight Crosswinds PDFDocument8 paginiMathematics of Flight Crosswinds PDFHassan Alazzie AmerÎncă nu există evaluări
- Ramos Math TrigonometryDocument25 paginiRamos Math TrigonometryaprilbagonÎncă nu există evaluări
- Ok 20231105155821476398 Classifying Triangles Practice NDocument4 paginiOk 20231105155821476398 Classifying Triangles Practice NCyril Danica LimareÎncă nu există evaluări
- Geometry Worksheet 1 - AnglesDocument13 paginiGeometry Worksheet 1 - AnglesAlexaÎncă nu există evaluări
- Angles, Angle Relationships, Trigo. FunctionsDocument8 paginiAngles, Angle Relationships, Trigo. FunctionsMÎncă nu există evaluări
- Me 418 4Document2 paginiMe 418 4Legna LegnaÎncă nu există evaluări
- Me 418 Part 4Document2 paginiMe 418 Part 4Angel BaldostamoÎncă nu există evaluări
- Objectives: Lesson Plan 4-7: The Law of Sines and The Law of CosinesDocument5 paginiObjectives: Lesson Plan 4-7: The Law of Sines and The Law of CosinesCristina BilogÎncă nu există evaluări
- Law of SinesDocument10 paginiLaw of SinesVeronika SinghÎncă nu există evaluări
- Problem SetDocument8 paginiProblem SetbaterbeeÎncă nu există evaluări
- Warm Up: 1. Identify The Pairs of AlternateDocument27 paginiWarm Up: 1. Identify The Pairs of AlternateRavin BoodhanÎncă nu există evaluări
- Angles of Elevation and DepressionDocument27 paginiAngles of Elevation and DepressionShivSantosh JhaÎncă nu există evaluări
- Trigo Bridging 1 and 2Document19 paginiTrigo Bridging 1 and 2blackmasque100% (1)
- Trigonometry Manual FinalDocument67 paginiTrigonometry Manual Finalun47542Încă nu există evaluări
- Textbook-Right Tri TrigDocument7 paginiTextbook-Right Tri Trigapi-251889735Încă nu există evaluări
- Plane Geometry Test QuestionaireDocument4 paginiPlane Geometry Test QuestionaireBeth VillaÎncă nu există evaluări
- Reviewer MathDocument261 paginiReviewer MathMac Jayson DiazÎncă nu există evaluări
- Geometry 2Document23 paginiGeometry 2Ayemyanandar KyiÎncă nu există evaluări
- 2016 Regional Geometry Exam Final PDFDocument15 pagini2016 Regional Geometry Exam Final PDFPartha SarathiÎncă nu există evaluări
- Me Diag 2 - DummyDocument3 paginiMe Diag 2 - DummyKrizia SantosÎncă nu există evaluări
- ALGEBRADocument4 paginiALGEBRAJevan SoberanoÎncă nu există evaluări
- 3.p Practice Test QuestionsDocument8 pagini3.p Practice Test Questionsmarkyvarona5Încă nu există evaluări
- Section 6.2 Law of Cosines: NameDocument2 paginiSection 6.2 Law of Cosines: Namesarasmile2009Încă nu există evaluări
- MODULESDocument11 paginiMODULESMatt ValenciaÎncă nu există evaluări
- PHYSICS M1 - With AnswerDocument9 paginiPHYSICS M1 - With AnswerayalarolenzÎncă nu există evaluări
- DG TE Ch09Document42 paginiDG TE Ch09Florecita RiosÎncă nu există evaluări
- Surface Area of Cuboid - Formula, Concept & QuestionsDocument11 paginiSurface Area of Cuboid - Formula, Concept & QuestionsRahul SinghÎncă nu există evaluări
- Bsed Math 3Document2 paginiBsed Math 3Vince Leo Panoncillon GonzalesÎncă nu există evaluări
- REVIEWDocument47 paginiREVIEWsheila lynn raut50% (2)
- Fourth Summative AssessmentDocument4 paginiFourth Summative AssessmentJolette StevensÎncă nu există evaluări
- Review Sheets Basic Mathematics MATH 020: A Summary of Concepts Needed To Be Successful in MathematicsDocument8 paginiReview Sheets Basic Mathematics MATH 020: A Summary of Concepts Needed To Be Successful in MathematicsSandy XiuÎncă nu există evaluări
- Pre Board in MathDocument19 paginiPre Board in MathSunde PascuaÎncă nu există evaluări
- CHAPTER 2.1, Trigonometry in Right Angled TriangleDocument10 paginiCHAPTER 2.1, Trigonometry in Right Angled TriangleaungminsfuÎncă nu există evaluări
- Midterm Exam (Math)Document9 paginiMidterm Exam (Math)Sherwin ConcepcionÎncă nu există evaluări
- 2019 MSTE MayDocument11 pagini2019 MSTE Maylorraine atienzaÎncă nu există evaluări
- Practice Problems - MathDocument4 paginiPractice Problems - MathKleinne KristenneÎncă nu există evaluări
- Mathematical Excursions 4Th Edition Aufmann Test Bank Full Chapter PDFDocument56 paginiMathematical Excursions 4Th Edition Aufmann Test Bank Full Chapter PDFTracySnydereigtc100% (13)
- Kami Export - Subject Complements-1 PDFDocument3 paginiKami Export - Subject Complements-1 PDFkcv kfdsaÎncă nu există evaluări
- GSD Puppy Training Essentials PDFDocument2 paginiGSD Puppy Training Essentials PDFseja saulÎncă nu există evaluări
- Indoor Air Quality Standard Procedures - 2014 RevDocument12 paginiIndoor Air Quality Standard Procedures - 2014 RevFioriAmeliaHathawayÎncă nu există evaluări
- Aquaculture Scoop May IssueDocument20 paginiAquaculture Scoop May IssueAquaculture ScoopÎncă nu există evaluări
- Free Electron TheoryDocument8 paginiFree Electron TheoryNeelam KapoorÎncă nu există evaluări
- Carrefour-SA Shopping Center TurkeyDocument2 paginiCarrefour-SA Shopping Center TurkeyVineet JogalekarÎncă nu există evaluări
- Petersen Coils Basic 20principle and ApplicationDocument3 paginiPetersen Coils Basic 20principle and ApplicationasotozuazuaÎncă nu există evaluări
- Arts Class: Lesson 01Document24 paginiArts Class: Lesson 01Lianne BryÎncă nu există evaluări
- Hashimoto's Thyroiditis: Veena RedkarDocument10 paginiHashimoto's Thyroiditis: Veena RedkarSan RedkarÎncă nu există evaluări
- Human Wildlife Conflict Resolution PDFDocument9 paginiHuman Wildlife Conflict Resolution PDFdemiÎncă nu există evaluări
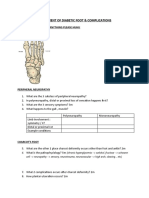
- Assessment of Diabetic FootDocument7 paginiAssessment of Diabetic FootChathiya Banu KrishenanÎncă nu există evaluări
- MC MATH 01 Syllabus SJCCDocument11 paginiMC MATH 01 Syllabus SJCCAcire NonacÎncă nu există evaluări
- LinkageDocument9 paginiLinkageHarshu JunghareÎncă nu există evaluări
- Nomenclatura SKFDocument1 paginăNomenclatura SKFJuan José MeroÎncă nu există evaluări
- W0L0XCF0866101640 (2006 Opel Corsa) PDFDocument7 paginiW0L0XCF0866101640 (2006 Opel Corsa) PDFgianyÎncă nu există evaluări
- Automatic Train OperationDocument6 paginiAutomatic Train OperationAnupam KhandelwalÎncă nu există evaluări
- Clocks (New) PDFDocument5 paginiClocks (New) PDFAbhay DabhadeÎncă nu există evaluări
- VavDocument8 paginiVavkprasad_56900Încă nu există evaluări
- Gujral FCMDocument102 paginiGujral FCMcandiddreamsÎncă nu există evaluări
- Test09 Eoc Algebra2 ReducedDocument33 paginiTest09 Eoc Algebra2 ReducedkristymadimikeÎncă nu există evaluări
- SMC VM Eu PDFDocument66 paginiSMC VM Eu PDFjoguvÎncă nu există evaluări
- Rectifier 5G High Density Embedded Power (3U Power Rack, Three Phase Four Wire) E...Document4 paginiRectifier 5G High Density Embedded Power (3U Power Rack, Three Phase Four Wire) E...Lintas LtiÎncă nu există evaluări
- Precision CatalogDocument256 paginiPrecision CatalogImad AghilaÎncă nu există evaluări
- Tabla de Avances de AcesoriosDocument3 paginiTabla de Avances de AcesoriosPedro Diaz UzcateguiÎncă nu există evaluări