Documente Academic
Documente Profesional
Documente Cultură
Models - Acdc.parallel Wires
Încărcat de
mrtabiehjTitlu original
Drepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
Models - Acdc.parallel Wires
Încărcat de
mrtabiehjDrepturi de autor:
Formate disponibile
Solved with COMSOL Multiphysics 4.
3a
Electromagnetic Forces on Parallel
Current-Carrying Wires
Introduction
One ampere is defined as the constant current in two straight parallel conductors of
infinite length and negligible circular cross section, placed one meter apart in vacuum,
that produces a force of 2107 newton per meter of length (N/m). This model shows
a setup of two parallel wires in the spirit of this definition, but with the difference that
the wires have finite cross sections.
For wires with circular cross section carrying a uniform current density as in this
example, the mutual magnetic force will be the same as for line currents. This can be
understood by the following arguments: Start from a situation where both wires are
line currents (I). Each line current will be subject to a Lorentz force (I B) where the
magnetic flux density (B) is the one produced by the other wire. Now, give one wire
a finite radius. It follows directly from circular symmetry and Maxwell-Ampres law
that, outside this wire, the produced flux density is exactly the same as before so the
force on the remaining line current is unaltered. Further, the net force on the wire with
the distributed current density must be of exactly the same magnitude (but with
opposite direction) as the force on the line current so that force did not change either.
If the two wires exchange places, the forces must still be the same and it follows from
symmetry that the force is independent of wire radius as long as the wire cross sections
do not intersect. The wires can even be cylindrical shells or any other shape with
circular symmetry. For an experimental setup, negligible cross section is required as
resistive voltage drop along the wires and Hall effect may cause electrostatic forces that
increase with wire radius but such effects are not included in this model.
The force between the wires is computed using two different methods: first
automatically by integrating the stress tensor on the boundaries, then by integrating
the volume (Lorentz) force density over the wire cross section. The results converge
to 2107 N/m for the 1 ampere definition, as expected.
Model Definition
The model is built using the 2D Magnetic Fields interface. The modeling plane is a
cross section of the two wires and the surrounding air.
2012 COMSOL
1 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES
Solved with COMSOL Multiphysics 4.3a
DOMAIN EQUATIONS
The equation formulation assumes that the only nonzero component of the magnetic
vector potential is Az. This corresponds to all currents being perpendicular to the
modeling plane. The following equation is solved:
e
( A z ) = J z
e
where is the permeability of the medium and J z is the externally applied current.
e
J z is set so that the applied current in the wires equals 1 A, but with different signs.
Surrounding the air is an infinite element domain. For details, see Infinite Elements in
AC/DC Module Users Guide.
Results and Discussion
The expression for the surface stress reads
1
T
n 1 T 2 = --- ( H B )n 1 + ( n 1 H )B
2
where n1 is the boundary normal pointing out from the conductor wire and T2 the
stress tensor of air. The closed line integral of this expression around the circumference
of either wire evaluates to 1.99107 N/m. The minus sign indicates that the force
between the wires is repulsive. The software automatically provides the coordinate
components of the force on each wire.
The volume force density is given by
F = J B = Je B , Je B , 0
z
y z
x
The surface integral of the x component of the volume force on the cross section of a
wire gives the result 2.00107 N/m.
By refining the mesh and re-solving the problem, you can verify that the solution with
both method converges to 2107 (N/m). The volume force density integral will
typically be the most accurate one for reasons explained in Calculating Accurate Fluxes
in the COMSOL Multiphysics Users Guide.
Model Library path: ACDC_Module/Verification_Models/parallel_wires
2 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES 2012 COMSOL
Solved with COMSOL Multiphysics 4.3a
Modeling Instructions
MODEL WIZARD
1 Go to the Model Wizard window.
2 Click the 2D button.
3 Click Next.
4 In the Add physics tree, select AC/DC>Magnetic Fields (mf).
5 Click Next.
6 Find the Studies subsection. In the tree, select Preset Studies>Stationary.
7 Click Finish.
GLOBAL DEFINITIONS
Parameters
1 In the Model Builder window, right-click Global Definitions and choose Parameters.
2 In the Parameters settings window, locate the Parameters section.
3 In the table, enter the following settings:
Name
Expression
Description
0.2[m]
Wire radius
I0
1[A]
Total current
J0
I0/(pi*r^2)
Current density
GEOMETRY 1
Circle 1
1 In the Model Builder window, under Model 1 right-click Geometry 1 and choose Circle.
2 In the Circle settings window, locate the Size and Shape section.
3 In the Radius edit field, type 1.5.
Circle 2
In the Model Builder window, right-click Geometry 1 and choose Circle.
Circle 3
1 Right-click Geometry 1 and choose Circle.
2 In the Circle settings window, locate the Size and Shape section.
3 In the Radius edit field, type r.
2012 COMSOL
3 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES
Solved with COMSOL Multiphysics 4.3a
4 Locate the Position section. In the x edit field, type 0.5.
Circle 4
1 Right-click Geometry 1 and choose Circle.
2 In the Circle settings window, locate the Size and Shape section.
3 In the Radius edit field, type r.
4 Locate the Position section. In the x edit field, type -0.5.
5 Click the Build All button.
You have now drawn the wires in their surrounding air domain. The outer circle will
constitute an infinite element.to make the geometry effectively extend to infinity. For
more information, please refer to the chapter Infinite Elements in the AC/DC Module
Users Guide.
DEFINITIONS
Define an infinite element region in the outer domains.
Infinite Element Domain 1
1 In the Model Builder window, under Model 1 right-click Definitions and choose Infinite
Element Domain.
2 Select Domain 1 only.
4 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES 2012 COMSOL
Solved with COMSOL Multiphysics 4.3a
3 In the Infinite Element Domain settings window, locate the Geometry section.
4 From the Type list, choose Cylindrical.
MATERIALS
Material Browser
1 In the Model Builder window, under Model 1 right-click Materials and choose Open
Material Browser.
2 In the Material Browser window, locate the Materials section.
3 In the tree, select Built-In>Air.
4 Right-click and choose Add Material to Model from the menu.
Air
By default, the first material you select will apply to your entire geometry. Air is defined
with a zero conductivity, and relative permittivity and permeability both equal to 1.
These properties are the same as those of vacuum, which is the assumed material in the
ampere definition. Since the model assumes a given uniform current distribution, it is
safe to use the same properties in the wires too.
MAGNETIC FIELDS
External Current Density 1
1 In the Model Builder window, under Model 1 right-click Magnetic Fields and choose
External Current Density.
2 Select Domain 3 only.
3 In the External Current Density settings window, locate the External Current Density
section.
4 In the Je table, enter the following settings:
0
J0
External Current Density 2
1 In the Model Builder window, right-click Magnetic Fields and choose External Current
Density.
2 Select Domain 4 only.
2012 COMSOL
5 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES
Solved with COMSOL Multiphysics 4.3a
3 In the External Current Density settings window, locate the External Current Density
section.
4 In the Je table, enter the following settings:
0
-J0
You have now completely defined the physics of this model. Adding force evaluations
will get you access to the Maxwell's stress tensors.
Force Calculation 1
1 Right-click Magnetic Fields and choose Force Calculation.
2 Select Domain 3 only.
3 In the Force Calculation settings window, locate the Force Calculation section.
4 In the Force name edit field, type wire1.
Force Calculation 2
1 Right-click Magnetic Fields and choose Force Calculation.
2 Select Domain 4 only.
3 In the Force Calculation settings window, locate the Force Calculation section.
4 In the Force name edit field, type wire2.
STUDY 1
In the Model Builder window, right-click Study 1 and choose Compute.
RESULTS
Magnetic flux density norm
The default plot shows the norm of the magnetic flux density. Note that the value
inside the infinite element domain has no physical relevance.
1 In the Model Builder window, under Results right-click Magnetic flux density norm and
choose Arrow Line.
2 In the Arrow Line settings window, click Replace Expression in the upper-right corner
of the Expression section. From the menu, choose Magnetic
Fields>Mechanical>Maxwell surface stress tensor (mf.nTx_wire1,...,mf.nTy_wire1).
3 Locate the Coloring and Style section. Select the Scale factor check box.
6 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES 2012 COMSOL
Solved with COMSOL Multiphysics 4.3a
4 In the associated edit field, type 300000.
5 From the Color list, choose Blue.
6 Click the Plot button.
7 Click the Zoom In button on the Graphics toolbar.
8 In the Model Builder window, right-click Magnetic flux density norm and choose Arrow
Line.
9 In the Arrow Line settings window, click Replace Expression in the upper-right corner
of the Expression section. From the menu, choose Magnetic
Fields>Mechanical>Maxwell surface stress tensor (mf.nTx_wire2,...,mf.nTy_wire2).
10 Locate the Coloring and Style section. Select the Scale factor check box.
11 In the associated edit field, type 300000.
12 From the Color list, choose Black.
13 Click the Plot button.
You are now looking at the Maxwell's stress tensor distribution on the surface of the
wires. The total force on each wired is evaluated as the surface integral of the stress
tensor, and stored in an automatically available expression.
2012 COMSOL
7 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES
Solved with COMSOL Multiphysics 4.3a
Derived Values
1 In the Model Builder window, under Results right-click Derived Values and choose
Global Evaluation.
2 In the Global Evaluation settings window, click Replace Expression in the upper-right
corner of the Expression section. From the menu, choose Magnetic
Fields>Mechanical>Electromagnetic force>Electromagnetic force, x component
(mf.Forcex_wire1).
3 Click the Evaluate button. The force in the x direction on the first wire will evaluate
to -1.99e-7 N/m.
4 In the Global Evaluation settings window, click Replace Expression in the upper-right
corner of the Expression section. From the menu, choose Magnetic
Fields>Mechanical>Electromagnetic force>Electromagnetic force, x component
(mf.Forcex_wire2).
5 Click the Evaluate button. As expected, the force on the second wire has a similar
value but the opposite sign.
Proceed to compare the values you just got with those from the Lorentz force
distribution.
6 In the Model Builder window, right-click Derived Values and choose
Integration>Surface Integration.
7 Select Domain 3 only.
8 In the Surface Integration settings window, click Replace Expression in the upper-right
corner of the Expression section. From the menu, choose Magnetic
Fields>Mechanical>Lorentz force contribution>Lorentz force contribution, x
component (mf.FLtzx).
9 Click the Evaluate button. This time, the value is even closer to -2e-7 N/m. When
applicable, Lorentz force integrals usually give more accurate results than the
Maxwell's stress tensor.
10 Select Domain 4 only.
11 Click the Evaluate button. Once again, integration over the second wire gives a
similar but positive result.
8 |
ELECTROMAGNETIC FORCES ON PARALLEL CURRENT-CARRYING WIRES 2012 COMSOL
S-ar putea să vă placă și
- The Yellow House: A Memoir (2019 National Book Award Winner)De la EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Evaluare: 4 din 5 stele4/5 (98)
- EnerLINE Medium Voltage Switchboards - SUBCOE - VFD, Power & Control Systems OEMDocument2 paginiEnerLINE Medium Voltage Switchboards - SUBCOE - VFD, Power & Control Systems OEMmrtabiehjÎncă nu există evaluări
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDe la EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeEvaluare: 4 din 5 stele4/5 (5795)
- Protection Relay Testing and CommissioningDocument56 paginiProtection Relay Testing and CommissioningmrtabiehjÎncă nu există evaluări
- Shoe Dog: A Memoir by the Creator of NikeDe la EverandShoe Dog: A Memoir by the Creator of NikeEvaluare: 4.5 din 5 stele4.5/5 (537)
- Danger: O&M Manual For 40-1200A (480/600 Vac) ATC-800 3-Position, Open/Closed Transition Contactor Based Transfer SwitchDocument1 paginăDanger: O&M Manual For 40-1200A (480/600 Vac) ATC-800 3-Position, Open/Closed Transition Contactor Based Transfer SwitchmrtabiehjÎncă nu există evaluări
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDe la EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureEvaluare: 4.5 din 5 stele4.5/5 (474)
- Power Systems, Substation Electrician Training: Points of InterestDocument4 paginiPower Systems, Substation Electrician Training: Points of InterestmrtabiehjÎncă nu există evaluări
- Grit: The Power of Passion and PerseveranceDe la EverandGrit: The Power of Passion and PerseveranceEvaluare: 4 din 5 stele4/5 (588)
- Tests SwitchesDocument31 paginiTests Switchesmrtabiehj100% (1)
- On Fire: The (Burning) Case for a Green New DealDe la EverandOn Fire: The (Burning) Case for a Green New DealEvaluare: 4 din 5 stele4/5 (74)
- Drive Communication Instruction Manual: March 2012 Part Number: 144-27025Document74 paginiDrive Communication Instruction Manual: March 2012 Part Number: 144-27025mrtabiehjÎncă nu există evaluări
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDe la EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryEvaluare: 3.5 din 5 stele3.5/5 (231)
- Smart 500Document138 paginiSmart 500mrtabiehj100% (2)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDe la EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceEvaluare: 4 din 5 stele4/5 (895)
- Ar Tower Detail SketchDocument3 paginiAr Tower Detail SketchmrtabiehjÎncă nu există evaluări
- Never Split the Difference: Negotiating As If Your Life Depended On ItDe la EverandNever Split the Difference: Negotiating As If Your Life Depended On ItEvaluare: 4.5 din 5 stele4.5/5 (838)
- TBD 616 OemDocument257 paginiTBD 616 OemmrtabiehjÎncă nu există evaluări
- The Little Book of Hygge: Danish Secrets to Happy LivingDe la EverandThe Little Book of Hygge: Danish Secrets to Happy LivingEvaluare: 3.5 din 5 stele3.5/5 (400)
- RIBE - B08 - Optofit - ADSS OPGW & OPPW PDFDocument104 paginiRIBE - B08 - Optofit - ADSS OPGW & OPPW PDFmrtabiehjÎncă nu există evaluări
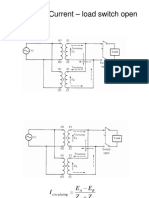
- Circulating Current - Load Switch OpenDocument10 paginiCirculating Current - Load Switch OpenmrtabiehjÎncă nu există evaluări
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDe la EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersEvaluare: 4.5 din 5 stele4.5/5 (345)
- Malik Tcpdump FiltersDocument41 paginiMalik Tcpdump FiltersombidasarÎncă nu există evaluări
- Aerated Static Pile Composting (ASP) VS Aerated (Turned) Windrow CompostingDocument2 paginiAerated Static Pile Composting (ASP) VS Aerated (Turned) Windrow CompostingRowel GanzonÎncă nu există evaluări
- The Unwinding: An Inner History of the New AmericaDe la EverandThe Unwinding: An Inner History of the New AmericaEvaluare: 4 din 5 stele4/5 (45)
- Trail Beaver Valley Edition of May 29, 2012 PennywiseDocument56 paginiTrail Beaver Valley Edition of May 29, 2012 PennywisePennywise PublishingÎncă nu există evaluări
- Team of Rivals: The Political Genius of Abraham LincolnDe la EverandTeam of Rivals: The Political Genius of Abraham LincolnEvaluare: 4.5 din 5 stele4.5/5 (234)
- This Tutorial Will Help To Test The Throttle Position Sensor On Your 1989 To 1997 1Document7 paginiThis Tutorial Will Help To Test The Throttle Position Sensor On Your 1989 To 1997 1HERBERT SITORUS100% (1)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDe la EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyEvaluare: 3.5 din 5 stele3.5/5 (2259)
- Dahua Video Conferencing SolutionDocument16 paginiDahua Video Conferencing SolutionDennis DubeÎncă nu există evaluări
- T BeamDocument17 paginiT BeamManojÎncă nu există evaluări
- Bharati AXA Life InsuranceDocument57 paginiBharati AXA Life InsuranceNaina_Dwivedi_6514100% (3)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDe la EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaEvaluare: 4.5 din 5 stele4.5/5 (266)
- OS Lab ManualDocument37 paginiOS Lab ManualVenkatanagasudheer ThummapudiÎncă nu există evaluări
- The Emperor of All Maladies: A Biography of CancerDe la EverandThe Emperor of All Maladies: A Biography of CancerEvaluare: 4.5 din 5 stele4.5/5 (271)
- A Study On Impact of Acne Vulgaris On Quality of LifeDocument7 paginiA Study On Impact of Acne Vulgaris On Quality of LifeIJAR JOURNALÎncă nu există evaluări
- Cylinder Clamp For N2 Cylinder 84L and FM-200 Cylinder 82.5LDocument1 paginăCylinder Clamp For N2 Cylinder 84L and FM-200 Cylinder 82.5LNguyễn Minh ThiệuÎncă nu există evaluări
- Diodat PDFDocument4 paginiDiodat PDFFatmir KelmendiÎncă nu există evaluări
- CHAPTER 22-Audit Evidence EvaluationDocument27 paginiCHAPTER 22-Audit Evidence EvaluationIryne Kim PalatanÎncă nu există evaluări
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDe la EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreEvaluare: 4 din 5 stele4/5 (1090)
- Jurnal Stamina: E-ISSN 2655-2515 P-ISSN 2655-1802Document9 paginiJurnal Stamina: E-ISSN 2655-2515 P-ISSN 2655-1802Yogi TioÎncă nu există evaluări
- Brigada EskwelaDocument4 paginiBrigada EskwelaJas Dela Serna SerniculaÎncă nu există evaluări
- Part 04 - Plumbing, Mechanical & Firefighting SpecificationsDocument210 paginiPart 04 - Plumbing, Mechanical & Firefighting Specificationsvtalex100% (1)
- Region VIII Schools Division of Tacloban City DLC V Sto. Niño Extension, Tacloban CityDocument3 paginiRegion VIII Schools Division of Tacloban City DLC V Sto. Niño Extension, Tacloban CityRikka EspedillaÎncă nu există evaluări
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)De la EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Evaluare: 4.5 din 5 stele4.5/5 (121)
- Hydraulic Power Unit: RE 51057, Edition: 2020-11, Bosch Rexroth AGDocument20 paginiHydraulic Power Unit: RE 51057, Edition: 2020-11, Bosch Rexroth AGHanzil HakeemÎncă nu există evaluări
- Vandex CrystallineDocument12 paginiVandex CrystallineJoseph ChenÎncă nu există evaluări
- 6 Elements of A Healthy ChurchDocument2 pagini6 Elements of A Healthy ChurchJayhia Malaga JarlegaÎncă nu există evaluări
- Daftar Kalibrasi Peralatan MedisDocument34 paginiDaftar Kalibrasi Peralatan Medisdiklat rssnÎncă nu există evaluări
- Principles of Care-Nursing For Children: Principle DescriptionDocument3 paginiPrinciples of Care-Nursing For Children: Principle DescriptionSanthosh.S.UÎncă nu există evaluări
- Standard Operating Procedure Template - Single PageDocument1 paginăStandard Operating Procedure Template - Single PagetesÎncă nu există evaluări
- Natural GeotextilesDocument27 paginiNatural GeotextilesDr Muhammad Mushtaq Mangat100% (1)
- QUIZ - PFRS 1 - FIRST TIME ADOPTION OF PFRSsDocument2 paginiQUIZ - PFRS 1 - FIRST TIME ADOPTION OF PFRSsGonzalo Jr. Ruales86% (7)
- Sample Rubrics MakingDocument4 paginiSample Rubrics MakingKerstmis “Scale” NataliaÎncă nu există evaluări
- Unclaimed Abandoned Vehicles Feb 2022Document66 paginiUnclaimed Abandoned Vehicles Feb 2022kumar himanshuÎncă nu există evaluări
- Her Body and Other Parties: StoriesDe la EverandHer Body and Other Parties: StoriesEvaluare: 4 din 5 stele4/5 (821)
- Fernbetätigte Armaturen: Remote Controlled Valve SystemsDocument14 paginiFernbetätigte Armaturen: Remote Controlled Valve SystemslequangÎncă nu există evaluări
- White Paper - Data Communication in Substation Automation System SAS - Part 1 Original 23353Document5 paginiWhite Paper - Data Communication in Substation Automation System SAS - Part 1 Original 23353sabrahimaÎncă nu există evaluări
- 785 TrucksDocument7 pagini785 TrucksJavier Pagan TorresÎncă nu există evaluări
- Computation of Total Income: Zenit - A KDK Software Software ProductDocument2 paginiComputation of Total Income: Zenit - A KDK Software Software ProductKartik RajputÎncă nu există evaluări