Documente Academic
Documente Profesional
Documente Cultură
Seismic Loading and Analysis in Esteem 7
Încărcat de
_jessecaDrepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
Seismic Loading and Analysis in Esteem 7
Încărcat de
_jessecaDrepturi de autor:
Formate disponibile
Esteem Technical Manual
Seismic loading and analysis
References
1. Nawy, Edward G.
Reinforced concrete: a fundamental approach / Edward G. Nawy. -4th ed., 2000
Chap. 15
2. Farzad Naeim
The Seismic Design Handbook
2nd Ed.,2001
pp. 140ff
3. International Code Council
International Building Code 2006 (IBC)
-o-
p154
Esteem Technical Manual
Formulation of seismic parameters
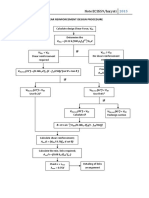
The following table outlines the steps in obtaining the coefficient Cs (Seismic Load Factor)
and k (Seisimic Distribution Exponent) required for the seismic load application. The "
Equivalent lateral force method" is used in Esteem 7 for earthquake loadings.
Steps Calculations
Description
1.
V = seismic base shear
Cs = seismic response
2.
3.
V = Cs.W
Cs = S DS/(R/I)
Condition 1:
Cs =calculated in
Dependent Parameter
coefficient or seismic load
factor
W = The effective seismic
weight fo the structure,
inclusive or 20% live
loading.
SDS = Design spectral
SS=Mapped Spectral
5%
damped
response acceleration at acceleration for short
short period.
periods, eg. 0.075g where design
g=9.81 N/kg.
SDS=2/3.S MS
Fa=Site coefficent from
SMS=Fa.SS
Table 15.2a of Ref. (1).
SD1 = Design spectral
response acceleration at
1 second period.
S1=Mapped Spectral
acceleration for 1 second
period, eg. 0.025g where
g=9.81 N/kg.
(2) above cannot
exceed the
following,
SD1=2/3.S M1
Cs = S D1/((R/I).T)
Fv=Site coefficent from
Table 15.2b of Ref. (1).
SM1=Fv.S1
4.
Condition 2:
Cs =calculated in
(2) above cannot
be taken less than
following,
Cs=0.044 SDS
In lieu of an analysis, an R = Response modification
approximate fundamental factor (see Table 1617.6
period can be used,
ref. (3))
(3/4)
Ta=CT.h
I=Occupancy importance
factor
h = Program will
automatically compute
CT=Building Period
the total height of
Coefficient
building.
5.
Assumptio
n
Condition 3:
For building and structures in seismic design
categories E or F and in buildings and
structures for which the 1-sec spectral
response, S1 is equal to or greater than
0.6g,
p155
5%
damped
design
Esteem Technical Manual
6.
Seismic
Distribution
Exponent, k
Based on building period,
T calculated above.
k=1 for T <=0.5 sec
k=2 for T >=2.5 sec
Interpolate linearly k
value for T between 0.5
and 2.5 sec.
Notes
:
1. Mapped Spectral accelerations, SS and S1 (Spectral Response Acceleration) are to be
obtained from published regional geographic charts. In absence of such charts, engineers
must use good judgment accordingly. See Figure 1613.5ff of the "International Building
Code (IBC) 2006" for US charts as example.
-o-
p156
Esteem Technical Manual
Site Classification, Table 1613.5.2 ref. (3)
Notes
:
1. As far as Esteem 7 is concerned, site classification affects the calculation of Cs when
Site Class E & F are selected. It invites the consideration of Condition 3 as outline in the
topic above.
-o-
p157
Esteem Technical Manual
Fa, Table 15.2a ref. (1)
Value of Site Coefficient Fa as a function of site class and mapped spectral response
acceleration at short periods (SS).
Site Class
A
B
C
D
E
F
SS =< 0.25
0.8
1.0
1.2
1.6
2.5
SS =< 0.50
0.8
1.0
1.2
1.4
1.7
SS =< 0.75
0.8
1.0
1.1
1.2
1.2
-o-
p158
SS =< 1.00
0.8
1.0
1.0
1.1
0.9
SS =< 1.25
0.8
1.0
1.0
1.0
Esteem Technical Manual
Fv, Table 15.2b ref. (1)
Value of Site Coefficient Fv as a function of site class and mapped spectral response
acceleration at 1.0 sec periods (S1).
Site Class
A
B
C
D
E
F
S1 =< 0.1
0.8
1.0
1.7
2.4
3.5
S1 =< 0.2
0.8
1.0
1.6
2.0
3.2
S1 =< 0.3
0.8
1.0
1.5
1.8
2.8
-o-
p159
S1 =< 0.4
0.8
1.0
1.4
1.6
2.4
S1 =< 0.5
0.8
1.0
1.3
1.5
Esteem Technical Manual
R, Table 1617.6 ref. (3)
extract of Table 1617.6 ref. (3) for Response modification coefficient R .
Basic Seismic-Force-Resisting System
Response
System Limitations and Building Height Limitations (m)
Modification
by Seismic Deisgn Categoryc as determined in IBC
C oefficient, R Section 1616.1
A&B
C
Dd
Ee
Ff
Bearing Wall System
Special reinforced concrete shear wall
Ordinary reinforced concrete shear wall
Detailed plain concrete shear walls
Ordinary plain concrete shear walls
Building Frame System
Ordinary reinforced concrete shear wall
Detailed plain concrete shear walls
Ordinary plain concrete shear walls
Moment Resistant Frames
Special reinforced concrete moment frames
Intermediate reinforced concrete moment
frames
Ordinary reinforced concrete moment
frames
Dual System with Special Moment
Frames
Special reinforced concrete shear walls
Ordinary reinforced concrete shear walls
Dual System with Intermediate
Moment Frames
Special reinforced concrete shear walls
Ordinary reinforced concrete shear walls
Shear wall-frame Interactive system with
ordinary reinforced concrete moement
frames and ordinary reinforced concrete
shear walls
5.5
4.5
2.5
1.5
NL
NL
NL
NL
NL
NL
NL
NP
NL
NL
NP
48.8
NP
NP
NP
NP
NP
NP
NP
48.8
NP
NP
NP
NP
NP
NP
NP
48.8
NP
NP
NP
NP
NP
NP
NP
5
3
2
NL
NL
NL
8
5
NL
NL
NL
NL
NL
NP
NL
NP
NL
NP
NLh
NP
NP
NP
NP
8
7
NL
NL
NL
NL
NL
NP
NL
NP
NL
NP
6
5.5
5.5
NL
NL
NL
NL
NL
NP
48.8
NP
NP
30.5
NP
NP
30.5
NP
NP
c NL = not limited and NP = not permitted
d limited to buildings with a height of 73.2m or less.
e limited to buildings with a height of 48.8m or less.
f Ordinary moment frame is permitted to be used in lieu of Intermediate moment frame in seismic design categories
B, and C.
h Ordinary moment frames of reinforced concrete are not permitted as a part of the seismic-force-resisting system
in seismic design category B structures fonded on Site Class E or F soils
-o-
p160
Esteem Technical Manual
I, Table 15.5 ref. (1)
-o-
p161
Esteem Technical Manual
Examples
Example to Ref. 1 (Nawy) page 693
A building of 5 storey of 2.9m height per floor (total height = 14.5m).
Building category II
Site Class B
Seismic group II (use in spectral response method)
Response modification method, R = 3.0
Occupancy importance factor, I = 1.25
From ground motion maps, S 1=0.42, Ss=0.85 (Site B with 5% damping)
Adjusted spectral response accelerations for site class effects:
o for S1=0.42, Fv=1.0
o
o
o
o
o
for SS=0.85, Fa=1.0
SMS=Fa.S S=1.0 x 0.85=0.85
SM1=Fv.S 1=1.0 x 0.42=0.42
SDS=2/3 . SMS=2/3 x 0.85 = 0.567
SD1=2/3 . SM1=2/3 x 0.42 = 0.278
CS=SDS /(R/I)=0.567/(3/1.25)=0.236 but cannot exceed
CS=SD1 /(R/I) . T
; Ta = CT h(3/4) = 0.085 {for moment resisting frames} . 14.5(3/4) = 0.63 sec
Hence, CS=SD1 /(R/I) . T = 0.278 /((3/1.25) x 0.63) = 0.184
k = 1+ (0.63-0.5)/(2.5-0.5)=1.065
Example 2
A building of 5 storey of 3m height per floor (total height = 15m).
Building category II
Site Class B
Seismic group II (use in spectral response method)
Response modification method, R = 3.0
Occupancy importance factor, I = 1.25
From ground motion maps, S 1=0.03, Ss=0.075 (Site B with 5% damping)
Adjusted spectral response accelerations for site class effects:
o for S1=0.03, Fv=0.8
o
o
o
o
o
for SS=0.075, Fa=0.8
SMS=Fa.S S=0.8 x 0.075=0.06
SM1=Fv.S 1=0.8 x 0.03=0.024
SDS=2/3 . SMS=2/3 x 0.06 = 0.04
SD1=2/3 . SM1=2/3 x 0.024 = 0.016
CS=SDS /(R/I)=0.04/(3/1.25)=0.0167 but cannot exceed
CS=SD1 /(R/I) . T
p162
Esteem Technical Manual
; Ta = CT h(3/4) = 0.085 {for moment resisting frames} . 15(3/4) = 0.648 sec
Hence, CS=SD1 /(R/I) . T = 0.016 /((3/1.25) x 0.648) = 0.01
k = 1+ (0.648-0.5)/(2.5-0.5)=1.074
-o-
p163
Esteem Technical Manual
CT, Building Period Coefficient, ref. (1)
-o-
p164
Esteem Technical Manual
Vertical Distribution of Forces
The lateral force Fx induced at any level can be determined from the following expressions
illustrated by Nawy.
Cvx = vertical distribution factor
V = total design lateral force or shear at the base of the building.
Wi and Wx = the portion of the total gravity load of the building, W, located or assigned to
Level i or x
hi and hx = the height from the base to level i or x
k = seismic distribution exponent
-o-
p165
S-ar putea să vă placă și
- Asce 7 Seismic ExampleDocument7 paginiAsce 7 Seismic ExampleKatherine Prado100% (1)
- Asce 7-05 Seismic Load CalculationDocument4 paginiAsce 7-05 Seismic Load Calculationอภิรักษ์ มานะกิจศิริสุทธิ100% (1)
- Column Base Plate DesignDocument5 paginiColumn Base Plate Design_jessecaÎncă nu există evaluări
- Plastic Properties HandbookDocument15 paginiPlastic Properties HandbookguilloteARGÎncă nu există evaluări
- Bridge Bearing2Document10 paginiBridge Bearing2sandbad2Încă nu există evaluări
- Derma Notes 22pages. DR - Vishwa Medical CoachingDocument23 paginiDerma Notes 22pages. DR - Vishwa Medical CoachingΝίκος ΣυρίγοςÎncă nu există evaluări
- Downdrag LectureDocument67 paginiDowndrag LectureAhmed ArafaÎncă nu există evaluări
- Specifications of The Application of Class Concrete Paving BlocksDocument10 paginiSpecifications of The Application of Class Concrete Paving BlockshonneyValadasÎncă nu există evaluări
- Coaxial Cable Attenuation ChartDocument6 paginiCoaxial Cable Attenuation ChartNam PhamÎncă nu există evaluări
- Johnson & Johnson Equity Research ReportDocument13 paginiJohnson & Johnson Equity Research ReportPraveen R V100% (3)
- Steel Beam DesignDocument27 paginiSteel Beam DesignSyazwi Akram Ab RazakÎncă nu există evaluări
- The Mooring Pattern Study For Q-Flex Type LNG Carriers Scheduled For Berthing at Ege Gaz Aliaga LNG TerminalDocument6 paginiThe Mooring Pattern Study For Q-Flex Type LNG Carriers Scheduled For Berthing at Ege Gaz Aliaga LNG TerminalMahad Abdi100% (1)
- MH5-C Prospekt PDFDocument16 paginiMH5-C Prospekt PDFvatasaÎncă nu există evaluări
- SDM Example 3 Steel SMF PDFDocument30 paginiSDM Example 3 Steel SMF PDFRicardoMallmaÎncă nu există evaluări
- Column Base Plate DesignDocument4 paginiColumn Base Plate Design_jessecaÎncă nu există evaluări
- Study On Utilization of Moringa Oleifera As CoagulationDocument3 paginiStudy On Utilization of Moringa Oleifera As CoagulationInternational Journal of Research in Engineering and TechnologyÎncă nu există evaluări
- Ibs CalculationDocument5 paginiIbs CalculationSiongyung KongÎncă nu există evaluări
- Traffic Characterization PDFDocument11 paginiTraffic Characterization PDFAlejandro GonzalezÎncă nu există evaluări
- RC Beam Torsion Design (BS8110 - Part2 - 1985)Document2 paginiRC Beam Torsion Design (BS8110 - Part2 - 1985)darkdkay100% (1)
- RobustnessDocument210 paginiRobustnessazhar ahmadÎncă nu există evaluări
- Flexible Pavement Thickness Design JKR MethodDocument3 paginiFlexible Pavement Thickness Design JKR MethodMohamad Shahrizal AliasÎncă nu există evaluări
- JPS MSMA Workshops On Sustainable Urban Stormwater Management Year 2016Document5 paginiJPS MSMA Workshops On Sustainable Urban Stormwater Management Year 2016Edison LimÎncă nu există evaluări
- BQ - Deep Foundation SampleDocument12 paginiBQ - Deep Foundation SampleNadhiera ShakeynaÎncă nu există evaluări
- EC2 Design CalculationsDocument81 paginiEC2 Design Calculationscollins unankaÎncă nu există evaluări
- Institutional Group Agencies For EducationDocument22 paginiInstitutional Group Agencies For EducationGlory Aroma100% (1)
- Steel BS Parameter PDFDocument8 paginiSteel BS Parameter PDFdpkÎncă nu există evaluări
- Detention Ponds 1Document7 paginiDetention Ponds 1mhilmi4100% (2)
- Rational Method Computation Time 30mins: Infravera SDN BHDDocument10 paginiRational Method Computation Time 30mins: Infravera SDN BHDazhar ahmadÎncă nu există evaluări
- Design and Reanalysis of Pile Cap Under EccentricityDocument8 paginiDesign and Reanalysis of Pile Cap Under EccentricityovikbasuÎncă nu există evaluări
- Skaa4412 SmkaDocument3 paginiSkaa4412 SmkaAmirBenYusoffÎncă nu există evaluări
- BS-1881-110 CONCRETE Making Test Cylinders From Fresh Con PDFDocument12 paginiBS-1881-110 CONCRETE Making Test Cylinders From Fresh Con PDFAshraf TomizehÎncă nu există evaluări
- EAS SeismicSingaporeRGDocument15 paginiEAS SeismicSingaporeRGblackwinterÎncă nu există evaluări
- TorsionDocument69 paginiTorsionpengniumÎncă nu există evaluări
- Chapter 1 - Introduction To RCDocument34 paginiChapter 1 - Introduction To RCBeanÎncă nu există evaluări
- Stability of Steel Framed Structures: Ir. Prof. Dr. Jeffrey ChiangDocument30 paginiStability of Steel Framed Structures: Ir. Prof. Dr. Jeffrey Chiangsam19961Încă nu există evaluări
- Full Shear Notes and ExampleDocument6 paginiFull Shear Notes and ExampleSiti MaimunahÎncă nu există evaluări
- Report Project EsteemDocument5 paginiReport Project EsteemKavi MaranÎncă nu există evaluări
- Sewerage Design Calculation For CO4Document6 paginiSewerage Design Calculation For CO4Mohd RafiqÎncă nu există evaluări
- ProtaStructure Suite 2016 Whats NewDocument41 paginiProtaStructure Suite 2016 Whats NewPlacid FabiloÎncă nu există evaluări
- MBDDocument13 paginiMBDAsraf MuidinÎncă nu există evaluări
- Body Corporate Guidelines PDFDocument17 paginiBody Corporate Guidelines PDFmaÎncă nu există evaluări
- G1 SG Pagoh SamplingDocument24 paginiG1 SG Pagoh SamplingbndrprdnaÎncă nu există evaluări
- BFC34803 - Test 1 - S2 20202021 - QuestionDocument4 paginiBFC34803 - Test 1 - S2 20202021 - Questionznyaphotmail.com0% (1)
- Detention Design SD01 - OSD SwinburneDocument2 paginiDetention Design SD01 - OSD SwinburneTony PedaÎncă nu există evaluări
- Release Notes 9.5.169.0 (27 April 2017)Document124 paginiRelease Notes 9.5.169.0 (27 April 2017)Nurmuliana Abdul WahabÎncă nu există evaluări
- Assignment1 - ECW557 - NURUL NABILAH MOKTAR PDFDocument11 paginiAssignment1 - ECW557 - NURUL NABILAH MOKTAR PDFNabilah.MoktarÎncă nu există evaluări
- Cid CiuDocument4 paginiCid CiuRazakMaidenÎncă nu există evaluări
- Projek Rekabentuk Walkwaybridge 2014 - 15Document6 paginiProjek Rekabentuk Walkwaybridge 2014 - 15HambaliÎncă nu există evaluări
- Lee Chai Peng Mohd. Shafeea Leman Kamaludin Hassan Bahari Md. Nasib Rashidah KarimDocument176 paginiLee Chai Peng Mohd. Shafeea Leman Kamaludin Hassan Bahari Md. Nasib Rashidah KarimsalmansaparudinÎncă nu există evaluări
- Topic 7 Flexible Pavement DesignDocument22 paginiTopic 7 Flexible Pavement DesignHanaÎncă nu există evaluări
- ECW571Document5 paginiECW571Ally ChorÎncă nu există evaluări
- Iem Osd Bulletin Drquek1 PDFDocument15 paginiIem Osd Bulletin Drquek1 PDFGan Chin PhangÎncă nu există evaluări
- Varying Peat in Sarawak and Some Geotechnial PropertiesDocument13 paginiVarying Peat in Sarawak and Some Geotechnial PropertiesSen HuÎncă nu există evaluări
- REPORTDocument20 paginiREPORTkishen972Încă nu există evaluări
- Continental Steel - Structural SteelDocument191 paginiContinental Steel - Structural SteelDesmond TongÎncă nu există evaluări
- Utilization of Compact Discs in Concrete Masonry Unit (Hollow Block) ProductionDocument7 paginiUtilization of Compact Discs in Concrete Masonry Unit (Hollow Block) ProductionAlexander Vaugn VillasisÎncă nu există evaluări
- 3rd Year 2nd Sem QuestionsDocument98 pagini3rd Year 2nd Sem Questionssourav_jucivilÎncă nu există evaluări
- Esteem 8 Brochure RevisedDocument4 paginiEsteem 8 Brochure RevisedaubarÎncă nu există evaluări
- D Internet Myiemorgmy Intranet Assets Doc Alldoc Document 10805 MS-SIRIM-190716 PDFDocument85 paginiD Internet Myiemorgmy Intranet Assets Doc Alldoc Document 10805 MS-SIRIM-190716 PDFHimura_Încă nu există evaluări
- Sensitivity, Thixotropy & Activity of Clays - Geotechnical EngineeringDocument5 paginiSensitivity, Thixotropy & Activity of Clays - Geotechnical EngineeringMike MikeÎncă nu există evaluări
- Seismic DesignDocument74 paginiSeismic DesignnathychidazÎncă nu există evaluări
- BS8110 Span-Depth Ratios PDFDocument1 paginăBS8110 Span-Depth Ratios PDFA KÎncă nu există evaluări
- Truss ReportDocument10 paginiTruss ReportFarrukhÎncă nu există evaluări
- CIVL6077 Ground Investigation and Soil Testing Lecture 4 In-Situ TestsDocument126 paginiCIVL6077 Ground Investigation and Soil Testing Lecture 4 In-Situ TestsHamza NadeemÎncă nu există evaluări
- Plastic Analysis of A StructureDocument19 paginiPlastic Analysis of A Structurejana42100% (1)
- BFC34803 - Test 1 - S2 20202021 - AnswerDocument8 paginiBFC34803 - Test 1 - S2 20202021 - AnswerAsyiqindiniaÎncă nu există evaluări
- BEM Sept08-Nov 08 (Engineering Practice)Document46 paginiBEM Sept08-Nov 08 (Engineering Practice)Md EliasÎncă nu există evaluări
- Celebrating Literacy in the Rwenzori Region: Lest We Forget: a Biographical Narrative of Uganda’S Youngest Member of Parliament, 1980-1985De la EverandCelebrating Literacy in the Rwenzori Region: Lest We Forget: a Biographical Narrative of Uganda’S Youngest Member of Parliament, 1980-1985Încă nu există evaluări
- Seismic Design of Bridges To EC8Document20 paginiSeismic Design of Bridges To EC8DomostatikosÎncă nu există evaluări
- Live As If You Were To Die Tomorrow Learn As If You Were To Live ForeverDocument1 paginăLive As If You Were To Die Tomorrow Learn As If You Were To Live Forever_jessecaÎncă nu există evaluări
- Albert EinsteinDocument1 paginăAlbert Einstein_jessecaÎncă nu există evaluări
- First They Ignore You, Then They Laugh at You, Then They Fight You, Then You WinDocument1 paginăFirst They Ignore You, Then They Laugh at You, Then They Fight You, Then You Win_jessecaÎncă nu există evaluări
- ABP12 - Q - AASHTO Vessel Collision Design of Highway Bridges (2009)Document60 paginiABP12 - Q - AASHTO Vessel Collision Design of Highway Bridges (2009)_jesseca0% (1)
- Bernard M. BaruchDocument1 paginăBernard M. Baruch_jessecaÎncă nu există evaluări
- Behold, I Stand at The Door and Knock. If Anyone Hears My Voice and Opens The Door, I Will Come in To Him and Eat With Him, and He With Me. Jesus ChristDocument1 paginăBehold, I Stand at The Door and Knock. If Anyone Hears My Voice and Opens The Door, I Will Come in To Him and Eat With Him, and He With Me. Jesus Christ_jessecaÎncă nu există evaluări
- Ms-Bridge 419 Klang Banting - 1Document1 paginăMs-Bridge 419 Klang Banting - 1_jessecaÎncă nu există evaluări
- A New Command I Give You: Love One Another. As I Have Loved You, So You Must Love One Another. Jesus ChristDocument1 paginăA New Command I Give You: Love One Another. As I Have Loved You, So You Must Love One Another. Jesus Christ_jessecaÎncă nu există evaluări
- Method Statement: 1) Cut Close Along Edge of Joint For Installation of Bridge JointDocument1 paginăMethod Statement: 1) Cut Close Along Edge of Joint For Installation of Bridge Joint_jessecaÎncă nu există evaluări
- Little Children, You Are From God, and Have Conquered Them For The One Who Is in You Is Greater Than The One Who Is in This World. Jesus ChristDocument1 paginăLittle Children, You Are From God, and Have Conquered Them For The One Who Is in You Is Greater Than The One Who Is in This World. Jesus Christ_jessecaÎncă nu există evaluări
- For Everyone Who Exalts Himself Will Be Humbled, and Everyone Who Humbles Himself Will Be Exalted. Jesus ChristDocument1 paginăFor Everyone Who Exalts Himself Will Be Humbled, and Everyone Who Humbles Himself Will Be Exalted. Jesus Christ_jessecaÎncă nu există evaluări
- Give To Everyone Who Begs From You and of Him Who Takes Away Your Goods Do Not Ask Them Again. and As You Wish That Men Would Do To You, Do So To Them. Jesus ChristDocument1 paginăGive To Everyone Who Begs From You and of Him Who Takes Away Your Goods Do Not Ask Them Again. and As You Wish That Men Would Do To You, Do So To Them. Jesus Christ_jessecaÎncă nu există evaluări
- So I Say To You, Ask and It Will Be Given To You Search, and You Will Find Knock, and The Door Will Be Opened For You. Jesus ChristDocument1 paginăSo I Say To You, Ask and It Will Be Given To You Search, and You Will Find Knock, and The Door Will Be Opened For You. Jesus Christ_jessecaÎncă nu există evaluări
- Do Not Let Your Hearts Be Troubled. Trust in God Trust Also in Me. Jesus ChristDocument1 paginăDo Not Let Your Hearts Be Troubled. Trust in God Trust Also in Me. Jesus Christ_jessecaÎncă nu există evaluări
- Let The One Among You Who Is Without Sin Be The First To Cast A Stone. Jesus ChristDocument1 paginăLet The One Among You Who Is Without Sin Be The First To Cast A Stone. Jesus Christ_jessecaÎncă nu există evaluări
- Ifihadanhourtosolvea Problem I'D Spend 55 Minutes Thinking About The Problem and 5 Minutes Thinking About Solutions."Document1 paginăIfihadanhourtosolvea Problem I'D Spend 55 Minutes Thinking About The Problem and 5 Minutes Thinking About Solutions."_jessecaÎncă nu există evaluări
- "Two Things Are Infinite: The Universe and Human Stupidity and I'm Not Sure About The Universe."Document1 pagină"Two Things Are Infinite: The Universe and Human Stupidity and I'm Not Sure About The Universe."_jessecaÎncă nu există evaluări
- Section N Layout For Type 2c Also Not YetDocument1 paginăSection N Layout For Type 2c Also Not Yet_jessecaÎncă nu există evaluări
- A Common Mistake That People Make When Trying To Design Something Completely Foolproof Is To Underestimate The Ingenuity of Complete Fools. - Douglas AdamsDocument1 paginăA Common Mistake That People Make When Trying To Design Something Completely Foolproof Is To Underestimate The Ingenuity of Complete Fools. - Douglas Adams_jessecaÎncă nu există evaluări
- General Notes For Post-Installed Reinforcing Bars SpecificationDocument1 paginăGeneral Notes For Post-Installed Reinforcing Bars Specification_jessecaÎncă nu există evaluări
- Do Not Be Anxious About Tomorrow, For Tomorrow Will Be Anxious For Itself. Let The Day's Own Trouble Be Sufficient For The DayDocument1 paginăDo Not Be Anxious About Tomorrow, For Tomorrow Will Be Anxious For Itself. Let The Day's Own Trouble Be Sufficient For The Day_jessecaÎncă nu există evaluări
- A Good Scientist Is A Person With Original Ideas. A Good Engineer Is A Person Who Makes A Design That Works With As Few Original Ideas As Possible - Freeman DysonDocument1 paginăA Good Scientist Is A Person With Original Ideas. A Good Engineer Is A Person Who Makes A Design That Works With As Few Original Ideas As Possible - Freeman Dyson_jessecaÎncă nu există evaluări
- Jesus Christ's QuoteDocument1 paginăJesus Christ's Quote_jessecaÎncă nu există evaluări
- 25 Middlegame Concepts Every Chess Player Must KnowDocument2 pagini25 Middlegame Concepts Every Chess Player Must KnowKasparicoÎncă nu există evaluări
- ReadingDocument205 paginiReadingHiền ThuÎncă nu există evaluări
- DirectionDocument1 paginăDirectionJessica BacaniÎncă nu există evaluări
- State Space ModelsDocument19 paginiState Space Modelswat2013rahulÎncă nu există evaluări
- ..Product CatalogueDocument56 pagini..Product Catalogue950 911Încă nu există evaluări
- World War II D-Day Invasion by SlidesgoDocument55 paginiWorld War II D-Day Invasion by SlidesgoPreston SandsÎncă nu există evaluări
- SafetyRelay CR30Document3 paginiSafetyRelay CR30Luis GuardiaÎncă nu există evaluări
- Chapter 5 Constructing An Agile Implementation PlanDocument4 paginiChapter 5 Constructing An Agile Implementation PlanAHMADÎncă nu există evaluări
- Instant Download Business in Action 7Th Edition Bovee Solutions Manual PDF ScribdDocument17 paginiInstant Download Business in Action 7Th Edition Bovee Solutions Manual PDF ScribdLance CorreaÎncă nu există evaluări
- Sample Learning Module As PatternDocument23 paginiSample Learning Module As PatternWilliam BulliganÎncă nu există evaluări
- ST Arduino Labs CombinedDocument80 paginiST Arduino Labs CombineddevProÎncă nu există evaluări
- Modular Q1 WK3-4Document3 paginiModular Q1 WK3-4JENIFFER DE LEONÎncă nu există evaluări
- Hele Grade4Document56 paginiHele Grade4Chard Gonzales100% (3)
- Traditional Perceptions and Treatment of Mental Illness in EthiopiaDocument7 paginiTraditional Perceptions and Treatment of Mental Illness in EthiopiaifriqiyahÎncă nu există evaluări
- AIIMS 2015 Solved PaperDocument436 paginiAIIMS 2015 Solved PaperSurya TejaÎncă nu există evaluări
- Multinational MarketingDocument11 paginiMultinational MarketingraghavelluruÎncă nu există evaluări
- 10 1108 - TQM 03 2020 0066 PDFDocument23 pagini10 1108 - TQM 03 2020 0066 PDFLejandra MÎncă nu există evaluări
- Lodge at The Ancient City Information Kit / Great ZimbabweDocument37 paginiLodge at The Ancient City Information Kit / Great ZimbabwecitysolutionsÎncă nu există evaluări
- Precursor Effects of Citric Acid and Citrates On Zno Crystal FormationDocument7 paginiPrecursor Effects of Citric Acid and Citrates On Zno Crystal FormationAlv R GraciaÎncă nu există evaluări
- Information Systems and Supply Chain ManagementDocument2 paginiInformation Systems and Supply Chain Managementvipinkandpal86Încă nu există evaluări
- Practice Problems - Electrochemical CellDocument5 paginiPractice Problems - Electrochemical CellYehia IbrahimÎncă nu există evaluări
- Safety Bulletin 09 - Emergency Escape Breathing Device - Product RecallDocument2 paginiSafety Bulletin 09 - Emergency Escape Breathing Device - Product RecallMuhammadÎncă nu există evaluări
- Active Hospital Network List For Vidal Health Insurance Tpa PVT LTD As On 01 Feb 2023Document119 paginiActive Hospital Network List For Vidal Health Insurance Tpa PVT LTD As On 01 Feb 2023jagdeepchkÎncă nu există evaluări