Documente Academic
Documente Profesional
Documente Cultură
CVEN2002 Week6
Încărcat de
Kai LiuDrepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
CVEN2002 Week6
Încărcat de
Kai LiuDrepturi de autor:
Formate disponibile
Statistics
CVEN2002/2702
Week 6
This lecture
5. Special random variables
5.6 Normal random variables
5.7 Checking if the data are normally distributed
6. Sampling distributions
6.1 Introduction
6.2 Estimation and sampling distribution
Additional reading: Sections 1.4, 2.4, 5.5 and 5.6 (pp.228-230)
in the textbook
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
2 / 43
5. Special random variables
Revision: the Normal distribution
A random variable is said to be normally distributed with parameters
and ( > 0), i.e.
X N (, ),
if its probability density function is given by
f (x) =
1
2
(x)2
2 2
( SX = R)
Unfortunately, no closed form exists for
! x
(y )2
1
e 22 dy
F (x) =
2
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
3 / 43
5. Special random variables
Revision: the Normal distribution
fX(x)
FX(x)
22
1/2
0
2
+ 2
+ 2
pdf f (x) = F (x)
cdf F (x)
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
4 / 43
5. Special random variables
Normal distribution: properties
It can be shown that, for any and ,
!
! +
(x)2
1
f (x) dx =
e 22 dx = 1
2
SX
Similarly, we can find
E(X ) =
and
Var(X ) =
1
2
1
2
xe
(x)2
2 2
dx =
(x )2 e
(x)2
2 2
dx = 2
Mean and variance of the Normal distribution
If X N (, ),
E(X ) =
CVEN2002/2702 (Statistics)
and
Var(X ) = 2
Dr Justin Wishart
( sd(X ) = )
Session 2, 2012 - Week 6
5 / 43
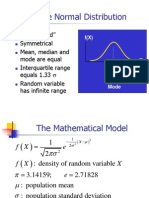
5. Special random variables
The Standard Normal distribution
The Standard Normal distribution is the Normal distribution with
= 0 and = 1. This yields
x2
1
f (x) = e 2
2
Usually, in this situation, the specific notation
.
.
f (x) = (x)
and
F (x) = (x)
is used, and a standard normal random variable is usually denoted Z
It directly follows from the preceding that
E(Z ) = 0
CVEN2002/2702 (Statistics)
and
Var(Z ) = 1
Dr Justin Wishart
(= sd(Z ))
Session 2, 2012 - Week 6
6 / 43
5. Special random variables
The Standard Normal distribution
(x)
(x)
1/2
pdf (x) = (x)
cdf (x)
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
7 / 43
5. Special random variables
Normal distribution: properties
An important observation is that all normal probability distribution
functions have the same bell shape
They only differ in where they are centred (at ) and in their spread
(quantified by )
N(40,2.5)
0.00
0.0
35
40
N(70,10)
N(10,5)
45
0.06
f(x)
0.02
0.00
0.00
0.01
0.04
0.02
0.03
0.08
0.04
f(x)
0.10
f(x)
0.05
0.2
0.1
f(x)
0.3
0.15
0.4
N(0,1)
40
50
60
70
80
90
100
CVEN2002/2702 (Statistics)
10
15
20
25
Dr Justin Wishart
Session 2, 2012 - Week 6
8 / 43
5. Special random variables
In Matlab, key in disttool and play with the interactive probability
function display tool (see Lab Week 6)
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
9 / 43
5. Special random variables
Normal distribution: standardisation
It is clear from the expression and the shape of the Normal pdf that if
X N (, ), then Y = aX + b is normally distributed with mean
E(Y ) = a + b and variance Var(Y ) = a2 2 (recall Sl. 24 & 28 Week 4)
The following result directly follows from the foregoing:
Property: Standardisation
If X N (, ), then
Z =
X
N (0, 1)
This linear transformation is called the standardisation of the normal
random variable X , as it transforms X into a standard normal random
variable Z (compare Slide 31, Week 4)
Standardisation will play a paramount role in what follows
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
10 / 43
5. Special random variables
Normal distribution: properties
This extremely important fact allows us to deduce any required
information for a given Normal distribution N (, ) from the features of
the simple standard normal distribution
For instance, for the standard pdf (x), it can be found that
"1
(x) dx = P(1 < Z < 1) 0.6827
"1
2
(x) dx = P(2 < Z < 2) 0.9545
"2
3
3 (x) dx = P(3 < Z < 3) 0.9973
This automatically translates to the general case X N (, ):
P( < X < + ) 0.6827
P( 2 < X < + 2) 0.9545
P( 3 < X < + 3) 0.9973
This is known as the 68-95-99 rule for normal distributions
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
11 / 43
5. Special random variables
Normal distribution: properties
For instance, suppose we are told that womens heights in a given
population follow a normal distribution with mean = 64.5 inches and
= 2.5 inches
we expect 68.27 % of women to be between
= 64.5 2.5 = 62 inches and + = 64.5 + 2.5 = 67 inches
tall, etc.
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
12 / 43
5. Special random variables
Normal distribution: remark
Theoretically, the domain of variation SX of a normally distributed
random variable X is R = (, +)
However, there is a 99.7% chance to find X between 3 and + 3
It almost impossible to find X outside that interval, and virtually
impossible to find it much further away from
there is in general no problem in modelling the distribution of a
positive quantity with a Normal distribution, provided is large
compared to
Typical examples include weight, height, or IQ of people
This also explains why 6 is sometimes called the width of the normal
distribution
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
13 / 43
5. Special random variables
Normal distribution: examples
Example
Suppose that Z N (0, 1). What is P(Z 1.25)?
In principle, this should be given by
P(Z 1.25) = (1.25) =
1.25
2
1
ex /2 dx
2
However, we know that this integral cannot be evaluated analytically
we must use software (command normcdf in Matlab) or the
Standard Normal table
Table I pp.560-561 in the textbook gives the area under the standard normal
curve to the left of z, that is
P(Z z) = (z)
table
Here we have just to read: P(Z 1.25) = (1.25) = 0.8944
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
14 / 43
5. Special random variables
Normal distribution: examples
Any other kind of probabilities must be written in terms of P(Z z) and
calculated from the value found in the table
Example
Suppose that Z N (0, 1). What is P(Z < 1.25)? What is P(Z > 1.25)?
What is P(0.38 Z < 1.25)?
As Z is a continuous random variable, P(Z < z) = P(Z z) for any z
table
P(Z < 1.25) = P(Z 1.25) = (1.25) = 0.8944
table
P(Z > 1.25) = 1 P(Z 1.25) = 1 (1.25) = 1 0.8944 = 0.1056
P(0.38 Z < 1.25) = P(Z < 1.25) P(Z < 0.38)
= P(Z 1.25) P(Z 0.38)
= (1.25) (0.38)
table
= 0.8944 0.3520 = 0.5424
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
15 / 43
5. Special random variables
Normal distribution: examples
Example 1.16 p.38 (textbook)
The time it takes a driver to react to the brake light on a decelerating vehicle
follows a Normal distribution having parameters = 1.25 sec and = 0.46
sec. In the long run, what proportion of reaction times will be between 1 and
1.75 sec?
We have X N (1.25, 0.46) and we desire P(1 X 1.75) . We have that
P(1 X 1.75) = P(X 1.75) P(X 1)
but unfortunately we do not have the N (1.25, 0.46)-table
However, we know that Z = X 1.25
0.46 N (0, 1) and we do have the N (0, 1)
table! use it!
$
#
1.75 1.25
X 1.25
table
= P(Z 1.09) = 0.8621
P(X 1.75) = P
0.46
0.46
table
Similarly, P(X 1) = P(Z 0.54) = (0.54) = 0.2946, so that
P(1 X 1.75) = 0.8621 0.2946 = 0.5675
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
16 / 43
5. Special random variables
Normal distribution: examples
Example
The actual amount of instant coffee that a filling machine puts into 4-ounce
jars may be looked upon as a random variable having a normal distribution
with = 0.04 ounce. If only 2% of the jars are to contain less than 4 ounces,
what should be the mean fill of these jars?
Let X denote the actual amount of coffee put into the jar by the machine
We have X N (, 0.04), with such that P(X 4) = 0.02
Hence,
0.02 = P(X 4) = P
4
X
0.04
0.04
#
$
4
=P Z
0.04
In the standard normal table, we can find that P(Z 2.05) 0.02
We conclude that
4
0.04
= 2.05, that is,
= 4 + 0.04 2.05 = 4.082 ounces
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
17 / 43
5. Special random variables
Normal distribution: quantiles
0.4
As in the previous example, we are sometimes given a probability and
asked to find the corresponding value z
P(Z < z ) = ,
for Z N (0, 1)
(x)
0.2
0.1
i.e.,
1
0.0
P(Z > z ) = 1 .
0.3
For instance, for any (0, 1), let
z be such that
2z
This value z is called the quantile of level of the standard normal
distribution
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
18 / 43
5. Special random variables
Normal distribution: quantiles
Some particular quantiles will be used extensively in subsequent
chapters. These are the quantiles of level 0.95, 0.975 and 0.995:
0.4
0.3
0.1
0.025
1.645
0.005
0.0
0.0
0.0
0.05
0.2
( x)
0.3
0.1
0.2
( x)
0.3
0.2
0.1
( x)
P(Z > 2.575) = 0.005
0.4
P(Z > 1.96) = 0.025,
0.4
P(Z > 1.645) = 0.05,
1.96
2.575
Note: by symmetry of the normal pdf, it is easy to see that
z1 = z
for instance, P(Z < 1.96) = 0.025
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
19 / 43
5. Special random variables
Some further properties of the Normal distribution
We know that if X N (, ), then aX + b is also normally distributed,
for any real values a and b (Slide 10)
This generalises further: if X1 N (1 , 1 ) and X2 N (2 , 2 ), and X1
and X2 are independent, then aX1 + bX2 is also normally distributed for
any real values a and b
Also, we can compute the parameters of the resulting distribution (see
Slides 38 and 45, Week 4)
Property
Suppose X1 N (1 , 1 ), X2 N (2 , 2 ) and X1 and X2 are
independent. Then, for any real values a and b,
#
$
%
2
2
2
2
aX1 + bX2 N a1 + b2 , a 1 + b 2
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
20 / 43
5. Special random variables
Some further properties of the Normal distribution
As a direct application of the preceding property, we have, with
X1 N (1 , 1 ) and X2 N (2 , 2 ), X1 and X2 independent,
$
#
$
#
%
%
X1 +X2 N 1 + 2 , 12 + 22 , X1 X2 N 1 2 , 12 + 22
Besides, the previous property can be readily extended to an arbitrary
number of independent normally distributed random variables
Example
Let X1 , X2 , X3 represent the times necessary to perform three successive
repair tasks at a certain service facility. Suppose they are independent normal
random variables with expected values 1 , 2 and 3 and variances 12 , 22
and 32 , respectively. What can be said about the distribution of X1 + X2 + X3 ?
From the previous property, we can conclude that
$
#
%
X1 + X2 + X3 N 1 + 2 + 3 , 12 + 22 + 32
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
21 / 43
5. Special random variables
Some further properties of the Normal distribution
Example (ctd.)
If 1 = 40 min, 2 = 50 min and 3 = 60 min, and 12 = 10 min2 , 22 = 12
min2 and 32 = 14 min2 , what is the probability that the full task would take
less than 160 min?
From the above, we have
Hence,
&
'
.
X = X1 + X2 + X3 N 150, 36 = 6
160 150
P(X 160) = P Z
6
#
CVEN2002/2702 (Statistics)
table
= P(Z 1.67) = (1.67) = = 0.9525
Dr Justin Wishart
Session 2, 2012 - Week 6
22 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
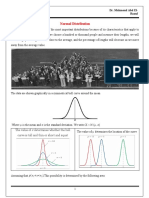
Checking if the data are normally distributed
Fact
Many of the statistical techniques presented in the coming chapters
are based on an assumption that the distribution of the random
variable of interest is (almost) normal
in many instances, we will need to check whether a data set
appears to be generated by a normally distributed random variable
How do we do that ?
Although they involve an element of subjective judgement, graphical
procedures are the most helpful for detecting serious departures from
normality
Some of the visual displays we have used earlier, such as the density
histogram (Slide 25, Week 2), can provide a first insight about the form
of the underlying distribution
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
23 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Density histograms to check for normality
Think of a density histogram as a piecewise constant function hn (x),
where n is the number of observations in the data set
then, if the r.v. X having generated the data has density f on a
support SX , it can be shown that, under some regularity
assumptions, for any x SX ,
hn (x) f (x)
as n (and the number of classes )
(the convergence hn (x) f (x) has to be understood in a particular
probabilistic sense, but details are beyond the scope of this course)
Concretely, the larger the number of observations, the more
similar the density histogram and the true (unknown) density f
are
look at the histogram and decide whether it looks enough like the
symmetric bell-shaped normal curve or not
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
24 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Density histograms to check for normality
Suppose we have a data set of size n = 50, drawn from a normal
distribution (but this, we ignore)
data set (dotchart) : n=50
Density histogram
35
40
45
35
40
45
0.10
0.00
0.00
0.05
0.05
f(x)
Density
0.10
0.15
0.15
density
35
40
45
the density histogram looks like the bell-shaped curve
Also, as both f (x) and the density histogram are scaled such that the
blue-ish purple areas are 1, they are easily superimposed and
compared
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
25 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Density histograms to check for normality
Look again at the density
histogram on Slide 26, Week 2
Density
Density
0.00
0.00
0.02
0.05
0.04
0.10
0.06
0.08
0.15
Look again at the (density)
histogram on Slide 17, Week 2
10
15
the histogram is symmetric and
bell-shaped, without outliers
the normality assumption is
reasonable
CVEN2002/2702 (Statistics)
20
20
40
60
80
clear lack of symmetry (skewed
to the right)
serious departure from
normality (Exponential?)
Dr Justin Wishart
Session 2, 2012 - Week 6
26 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Quantile plots
Density histograms are easy to use; however, they are usually not
really reliable indicators of the distributional form unless the number of
observations is very large
another special graph, called a normal quantile plot, is more
effective in detecting departure from normality
The plot essentially compares the data ordered from smallest to
largest with what to expect to get for the smallest to largest in a sample
of that size if the theoretical distribution from which the data have come
is normal
if the data were effectively selected from the normal distribution, the
two sets of values should be reasonably close to one another
Note: a quantile plot is also sometimes called qq-plot
( command in Matlab: qqplot)
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
27 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Quantile plots
Procedure for building a quantile plot:
observations {x1 , x2 , . . . , xn }
ordered observations: x(1) x(2) . . . x(n)
cumulative probabilities i = i0.5
n , for all i = 1, . . . , n
standard normal quantiles of level i : for all i = 1, . . . , n, zi
chosen such that P(Z zi ) = i , where Z N (0, 1)
Quantile plot: plot the n pairs (x(i) , zi )
If the sample comes from the Standard Normal distribution, x(i) zi
and the points would fall close to a 45 straight line passing by (0,0)
If the sample comes from some other normal distribution, the points
would still fall around a straight line, as there is a linear relationship
between the quantiles of N (, ) and the standard normal quantiles
Fact
If the sample comes from some normal distribution, the points should
follow (at least approximately) a straight line
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
28 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Quantile plots: examples
The figure below displays quantile plots for the previous two examples
quantile plot
quantile plot
Theoretical Quantiles
Theoretical Quantiles
10
15
Sample Quantiles
20
40
60
80
Sample Quantiles
the normality assumption appears acceptable for the first data set,
not at all for the second
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
29 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Transforming observations
When the density histogram and the qq-plot indicate that the
assumption of a normal distribution is invalid, transformations of the
data can often improve the agreement with normality (see lab classes
2 & 4)
Scientists regularly express their observations in natural logs
Lets look again at the seeded clouds rainfall data (Slide 9, Week 1)
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
30 / 43
5. Special random variables
5.7 Checking if the data are normally distributed
Transforming observations
Apart from log, other transformations may be useful:
1
,
x
x,
x,
x 2,
x3
If the observations are positive and the distribution has
a long tail on
the right, then concave transformations like log(x) or x put the large
values down farther than they pull the central or small values
observations more symmetric
Convex transformations work the other way
If the transformed observations are approximately normal (check with
a quantile plot), it is usually advantageous to use the normality of this
new scale to perform any statistical analysis
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
31 / 43
6. Sampling distributions
6. Sampling distributions
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
32 / 43
6. Sampling distributions
6.1 Introduction
Statistical Inference: Introduction
In this chapter, we introduce the last main topic for this course:
statistical inference (that will keep us busy until the end)
Recall (Lecture 1) the general problem that is addressed:
statistical methods are used to draw conclusions and make decisions
about a population of interest
however, for some reasons, we have no access to the whole population
and we must do with observations on a subset of the population only.
That subset is called the sample
if the sample is effectively representative of the population, what we
observe on the sample can be generalised to the population as a whole,
at least to some extent ...
... taking chance factors properly into account
from what we have learned about descriptive statistics, probabilities and
random variables in the previous chapters, we should now be able to set
all that to music
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
33 / 43
6. Sampling distributions
6.1 Introduction
Statistical Inference: Introduction
Populations are often described by the distribution of their values
for instance, it is quite common practice to refer to a normal
population, when the variable of interest is thought to be
normally distributed
In statistical inference, we focus on drawing conclusions about one
parameter describing the population
In engineering, the parameters we are mainly interested in are
the mean of the population
the variance 2 (or standard deviation ) of the population
the proportion of individuals in the population that belong to a
class of interest
the difference in means of two sub-populations, 1 2
the difference in two sub-populations proportions, 1 2
These parameters are unknown (otherwise, no need to make
inferences about them) the first part of the process is thus to
estimate the unknown parameters
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
34 / 43
6. Sampling distributions
6.1 Introduction
Random sampling
The importance of random sampling has been emphasised in
Lecture 1:
to assure that a sample is representative of the population from
which it is obtained, and
to provide a framework for the application of probability theory to
problems of sampling
As we said, the assumption of random sampling is very important: if
the sample is not random and is based on judgement or flawed in
some other way, then statistical methods will not work properly and will
lead to incorrect decisions
Therefore, we should now properly define a random sample
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
35 / 43
6. Sampling distributions
6.1 Introduction
Random sampling
Before a sample of size n is selected at random from the population,
the observations are modelled as random variables X1 , X2 , . . . , Xn
Definition
The set of observations X1 , X2 , . . . , Xn constitutes a random sample if
1
the Xi s are independent random variables, and
every Xi has the same probability distribution
This is often abbreviated to i.i.d., for independent and identically distributed
it is common to talk about an i.i.d. sample
We also apply the terms random sample to the set of observed values
x1 , x2 , . . . , xn
of the random variables, but this should not cause any confusion
Note: as usual, the lower case distinguishes the realisation of a random
sample (the actual data) from the upper case, which represents the random
variables before they are observed
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
36 / 43
6. Sampling distributions
6.2 Estimation and sampling distribution
Statistic, estimator and sampling distribution
A numerical measure calculated from the sample is called a statistic
Denote the unknown parameter of interest (so this can be , 2 , or
any other parameter of interest to us)
The only information we have to estimate that parameter is the
information contained in the sample
an estimator of must be a statistic, i.e. a function of the sample
= h(X1 , X2 , . . . , Xn )
Note that an estimator is a random variable, as it is a function of
random variables it must have a distribution
That distribution is called a sampling distribution, and it generally
depends on the population distribution and the sample size
takes on a particular value
After the sample has been selected,
= h(x1 , x2 , . . . , xn ), called the estimate of
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
37 / 43
6. Sampling distributions
6.2 Estimation and sampling distribution
Estimation: some remarks
Remark: the hat notation conventionally distinguishes the
or estimate )
from the true
sample-based quantities (estimator
population parameter (). Also, as usual, capital letters denote the
whereas lower-case letters are for particular
random variables, like ,
numerical values, like
two notable exceptions are:
; its observed value,
the sample mean, usually denoted X
calculated once we have observed a sample x1 , x2 , . . . , xn , is
denoted x
the sample standard deviation (variance), usually denoted S (S 2 );
its observed value, calculated once we have observed a sample
x1 , x2 , . . . , xn , is denoted s (s2 )
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
38 / 43
6. Sampling distributions
6.2 Estimation and sampling distribution
An example: estimating in a normal population
Suppose that the random variable X of interest is normally distributed, with
unknown mean and known standard deviation
From a(
random sample, a natural estimator for is the sample mean
= 1 n Xi , whose observed value is x = 1 (n xi (= estimate)
X
i=1
i=1
n
n
As the sample is random, it should be representative of the whole population,
and the population mean should be close to the observed sample mean x
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
39 / 43
6. Sampling distributions
6.2 Estimation and sampling distribution
An example: estimating in a normal population
What does that mean, should be close to x ?
the sampling distribution will answer this question
We know that each Xi in the sample follows the N (, ) distribution,
and they are independent (i.i.d. sample)
Then, because linear combinations of independent normal r.v. remain
normally distributed (Slides 20-21), we conclude that
n
)
=1
X
Xi
n
i=1
has a normal distribution with expectation
, n
n
n
)
)
* +
1
1)
i.d. 1
E X =E
Xi =
E(Xi ) =
=
n
n
n
i=1
and variance
* +
= Var
Var X
CVEN2002/2702 (Statistics)
1)
Xi
n
i=1
i=1
i.
i=1
n
n
)
1 )
2
i.d. 1
2
Var(X
)
=
=
i
n
n2
n2
i=1
Dr Justin Wishart
i=1
Session 2, 2012 - Week 6
40 / 43
6. Sampling distributions
6.2 Estimation and sampling distribution
An example: estimating in a normal population
is
the sampling distribution of X
$
#
X N ,
n
if the population is normal
2.0
sampling distribution of sample mean (normal population)
1.5
1.0
0.5
the larger the sample, the
more accurate the estimation
is
n=1
n=2
n=4
n=10
n=25
0.0
is a normal random variable,
X
centred about the true population
mean , and with spread becoming
more and more reduced as the
sample size increases
3 2
+ 2 + 3
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
41 / 43
6. Sampling distributions
6.2 Estimation and sampling distribution
Example
A sample of n = 28 heavy smoking men aged between 35 and 57, had a
sample mean testosterone level of 795.1 nanograms per decilitre. In the
general population of non smoking men of this age, we can assume that
testosterone is normally distributed with mean 620.6 and standard deviation
of 201.5. Are the results for the sample of smokers consistent with the
distribution for non-smokers?
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
42 / 43
Objectives
Objectives
Now you should be able to:
Calculate probabilities, determine mean, variance and standard
deviation for normal distributions
Standardise normal random variables, and understand why this is
useful
Use the table for the cdf of a standard normal distribution to
determine probabilities of interest
Explain the general concepts of estimating the parameters of a
population, in particular the difference between estimator and
estimate, and the role played by the sampling distribution of an
estimator
Illustrate those concepts with the particular case of the estimation
of the mean in a normal population
Recommended exercises Q31, Q33 p.41, Q35, Q37 p.42, Q73 p.58,
Q27 p.78, Q47 p.93, Q65 p.97, Q51, Q53 p.237
CVEN2002/2702 (Statistics)
Dr Justin Wishart
Session 2, 2012 - Week 6
43 / 43
S-ar putea să vă placă și
- Application of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsDe la EverandApplication of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsEvaluare: 5 din 5 stele5/5 (1)
- Special Continuous Probability Distributions Normal Distribution IIDocument24 paginiSpecial Continuous Probability Distributions Normal Distribution IIAyush BhadauriaÎncă nu există evaluări
- Mathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsDe la EverandMathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsÎncă nu există evaluări
- Probability distributions and sampling formulasDocument8 paginiProbability distributions and sampling formulasAlan TruongÎncă nu există evaluări
- Assignment 2 AnswersDocument18 paginiAssignment 2 AnswersIvonne NavasÎncă nu există evaluări
- Statistics 514 Design of Experiments Topic 2 OverviewDocument14 paginiStatistics 514 Design of Experiments Topic 2 OverviewVedha ThangavelÎncă nu există evaluări
- Probability Distributions ExplainedDocument17 paginiProbability Distributions ExplainedAnad DanaÎncă nu există evaluări
- Probability Distributions ExplainedDocument63 paginiProbability Distributions ExplainedPranva EshwarÎncă nu există evaluări
- Haan C T Statistical Methods in Hydrology SolutionDocument17 paginiHaan C T Statistical Methods in Hydrology Solutiongizem duralÎncă nu există evaluări
- Joint Distribution, Covariance, Correlation, Moments, Binomial, Normal, Poisson DistributionsDocument11 paginiJoint Distribution, Covariance, Correlation, Moments, Binomial, Normal, Poisson DistributionsKanchana RandallÎncă nu există evaluări
- Normal Distribution PDFDocument10 paginiNormal Distribution PDFsamriddha_671019633Încă nu există evaluări
- 5 BMDocument20 pagini5 BMNaailah نائلة MaudarunÎncă nu există evaluări
- Introduction Statistics Imperial College LondonDocument474 paginiIntroduction Statistics Imperial College Londoncmtinv50% (2)
- Chapter 6 Statistics For EngineerDocument16 paginiChapter 6 Statistics For EngineerZAINAL NAEMÎncă nu există evaluări
- Week4 PDFDocument50 paginiWeek4 PDFKai LiuÎncă nu există evaluări
- Introduction To The Normal Distribution PDFDocument6 paginiIntroduction To The Normal Distribution PDFwolfretonmathsÎncă nu există evaluări
- Confidence Intervals with σ unknownDocument9 paginiConfidence Intervals with σ unknownInnocent HarryÎncă nu există evaluări
- Continuous Probability Distributions and the Normal CurveDocument57 paginiContinuous Probability Distributions and the Normal CurveAkshay VetalÎncă nu există evaluări
- Probability DistributionsDocument17 paginiProbability Distributionstamann2004Încă nu există evaluări
- Solution CVEN2002 Solutions 1 7Document22 paginiSolution CVEN2002 Solutions 1 7Kai LiuÎncă nu există evaluări
- Applied Statistics and Probability For Engineers, 5th EditionDocument23 paginiApplied Statistics and Probability For Engineers, 5th EditionMuhammadHazmiMokhtar75% (4)
- Finals (STS)Document120 paginiFinals (STS)Johnleo AtienzaÎncă nu există evaluări
- CVEN2002 Week11Document49 paginiCVEN2002 Week11Kai LiuÎncă nu există evaluări
- Applied Statistics: Normal DistributionDocument13 paginiApplied Statistics: Normal Distributioniiyousefgame YTÎncă nu există evaluări
- Sta108 Group10 Project2 21december17Document13 paginiSta108 Group10 Project2 21december17FarahSyazwani100% (2)
- Examples of Continuous Probability Distributions:: The Normal and Standard NormalDocument57 paginiExamples of Continuous Probability Distributions:: The Normal and Standard NormalPawan JajuÎncă nu există evaluări
- CVEN2002 Week5Document43 paginiCVEN2002 Week5Kai LiuÎncă nu există evaluări
- 2.3 Probability DistributionsDocument41 pagini2.3 Probability DistributionsPatricia Nicole BautistaÎncă nu există evaluări
- Expectation and VarianceDocument16 paginiExpectation and VarianceWahab HassanÎncă nu există evaluări
- The Normal Distribution and Other Continuous Distribution: Dr. K. M. Salah UddinDocument50 paginiThe Normal Distribution and Other Continuous Distribution: Dr. K. M. Salah UddinfaisalÎncă nu există evaluări
- Normal DistributionDocument21 paginiNormal DistributionRajesh DwivediÎncă nu există evaluări
- Analysis of Categorical Data: Learning ObjectivesDocument34 paginiAnalysis of Categorical Data: Learning Objectives2oooveeeÎncă nu există evaluări
- Applied Probability Lecture Notes (OS2103Document22 paginiApplied Probability Lecture Notes (OS2103Tayyab ZafarÎncă nu există evaluări
- 4.3 Normal Probability Distributions: The Most Important Probability Distribution in StatisticsDocument37 pagini4.3 Normal Probability Distributions: The Most Important Probability Distribution in StatisticsNelson ChambiÎncă nu există evaluări
- Statistics FormulasDocument8 paginiStatistics Formulascem9066100% (3)
- Normal Distribution NotesDocument30 paginiNormal Distribution NotesFolad1090% (1)
- Standard Normal Distribution ProbabilitiesDocument13 paginiStandard Normal Distribution ProbabilitiesAlejandro SanhuezaÎncă nu există evaluări
- Ch3c Random Variables ContinuousDocument80 paginiCh3c Random Variables Continuouskhawla2789Încă nu există evaluări
- Normal Distribution: MATH30-6 Probability and StatisticsDocument17 paginiNormal Distribution: MATH30-6 Probability and StatisticsmisakaÎncă nu există evaluări
- The Normal DistributionDocument44 paginiThe Normal DistributionviayÎncă nu există evaluări
- 2 PDFDocument12 pagini2 PDFGag PafÎncă nu există evaluări
- Pertemuan 7Document17 paginiPertemuan 7budiabuyÎncă nu există evaluări
- Normal DistributionDocument10 paginiNormal DistributionLello FloÎncă nu există evaluări
- Term I, 10/11Document1 paginăTerm I, 10/11Xue Jing CongÎncă nu există evaluări
- SP2009F - Lecture03 - Maximum Likelihood Estimation (Parametric Methods)Document23 paginiSP2009F - Lecture03 - Maximum Likelihood Estimation (Parametric Methods)César Isabel PedroÎncă nu există evaluări
- Ken Black QA ch10Document47 paginiKen Black QA ch10Rushabh VoraÎncă nu există evaluări
- PSTAT 172A Homework Solutions Life TablesDocument14 paginiPSTAT 172A Homework Solutions Life TablesInstantRamen100% (2)
- Unit 1 - 03Document10 paginiUnit 1 - 03Raja RamachandranÎncă nu există evaluări
- Handout: Two Sample Hypothesis Testing and Inference ForDocument5 paginiHandout: Two Sample Hypothesis Testing and Inference Forsumanta1234Încă nu există evaluări
- Whole Digital Communication PPT-libreDocument319 paginiWhole Digital Communication PPT-librePiyush GuptaÎncă nu există evaluări
- H2 Maths Normal DistributionDocument14 paginiH2 Maths Normal Distributionpiyush raghavÎncă nu există evaluări
- AnovaDocument105 paginiAnovaasdasdas asdasdasdsadsasddssaÎncă nu există evaluări
- Additional Mathematics F5 Probability DistributionDocument9 paginiAdditional Mathematics F5 Probability DistributionFazlina MustafaÎncă nu există evaluări
- ECONOMICSRGUDocument105 paginiECONOMICSRGUDaniel DuraiÎncă nu există evaluări
- BS UNIT 2 Normal Distribution NewDocument41 paginiBS UNIT 2 Normal Distribution NewSherona ReidÎncă nu există evaluări
- Bivariate Normal 1 With Answers PDFDocument22 paginiBivariate Normal 1 With Answers PDFdÎncă nu există evaluări
- Comparing Means of Two Populations with Unknown and Equal VariancesDocument23 paginiComparing Means of Two Populations with Unknown and Equal VariancesAbdullah Al MughramÎncă nu există evaluări
- Stats Mean, Variance and Standard DeviationDocument3 paginiStats Mean, Variance and Standard DeviationJhanelle Martin0% (1)
- Chapter 8Document7 paginiChapter 8sezarozoldekÎncă nu există evaluări
- Tablas y Formulas Triola 9 EdDocument8 paginiTablas y Formulas Triola 9 EdJhonny Romero RaveloÎncă nu există evaluări
- Solution CVEN2002 Solutions 1 7Document22 paginiSolution CVEN2002 Solutions 1 7Kai LiuÎncă nu există evaluări
- CVEN2002 Week7Document43 paginiCVEN2002 Week7Kai LiuÎncă nu există evaluări
- CVEN2002 Week11Document49 paginiCVEN2002 Week11Kai LiuÎncă nu există evaluări
- Week1 PDFDocument35 paginiWeek1 PDFKai LiuÎncă nu există evaluări
- CVEN2002 Week10Document53 paginiCVEN2002 Week10Kai LiuÎncă nu există evaluări
- CVEN2002 Week8Document36 paginiCVEN2002 Week8Kai LiuÎncă nu există evaluări
- CVEN2002 Week12Document48 paginiCVEN2002 Week12Kai LiuÎncă nu există evaluări
- CVEN2002 Week5Document43 paginiCVEN2002 Week5Kai LiuÎncă nu există evaluări
- CVEN2002 Week9Document45 paginiCVEN2002 Week9Kai LiuÎncă nu există evaluări
- Week4 PDFDocument50 paginiWeek4 PDFKai LiuÎncă nu există evaluări
- Week3 PDFDocument40 paginiWeek3 PDFKai LiuÎncă nu există evaluări
- Week2 PDFDocument58 paginiWeek2 PDFKai LiuÎncă nu există evaluări
- Statistics and Probability: Sampling DistributionsDocument62 paginiStatistics and Probability: Sampling DistributionsKyle Sucalo De LeonÎncă nu există evaluări
- Report: Mean (Expected Value) of A Discrete Random Variable 100%Document2 paginiReport: Mean (Expected Value) of A Discrete Random Variable 100%abel mahendraÎncă nu există evaluări
- Module 5 - Probability and StatisticsDocument2 paginiModule 5 - Probability and StatisticsMichelleÎncă nu există evaluări
- Assignment 1Document2 paginiAssignment 1Shubham AcharyaÎncă nu există evaluări
- CH Var Basic PDFDocument48 paginiCH Var Basic PDFTPNÎncă nu există evaluări
- Bayesian Statistical MethodsDocument288 paginiBayesian Statistical Methodsmekkawi6650100% (7)
- JBF AcerbiTascheDocument18 paginiJBF AcerbiTaschemindlinjasÎncă nu există evaluări
- Chapter 1 - ProbabilityDocument27 paginiChapter 1 - ProbabilityShehan De SilvaÎncă nu există evaluări
- BUS232 Spring 2024 A4 (2)Document4 paginiBUS232 Spring 2024 A4 (2)BaniÎncă nu există evaluări
- Ps 1Document6 paginiPs 1Matt StapleÎncă nu există evaluări
- Data Analysis and Probability CalculationsDocument10 paginiData Analysis and Probability Calculationsdo minh tuanÎncă nu există evaluări
- Mathematics QuestionsDocument9 paginiMathematics Questionsvinay_1301100% (1)
- Hull: Options, Futures, and Other Derivatives, Tenth Edition Chapter 23: Estimating Volatilities and Correlations Multiple Choice Test BankDocument4 paginiHull: Options, Futures, and Other Derivatives, Tenth Edition Chapter 23: Estimating Volatilities and Correlations Multiple Choice Test BankKevin Molly KamrathÎncă nu există evaluări
- Excel ProbabilityDocument21 paginiExcel ProbabilityriemannadiÎncă nu există evaluări
- AI Mod5@AzDOCUMENTSinDocument40 paginiAI Mod5@AzDOCUMENTSinK SubramanyeshwaraÎncă nu există evaluări
- Belief, Probability and ExchangeabilityDocument17 paginiBelief, Probability and Exchangeabilityxiuxian liÎncă nu există evaluări
- Forecasting The Return Volatility of The Exchange RateDocument53 paginiForecasting The Return Volatility of The Exchange RateProdan IoanaÎncă nu există evaluări
- Probability Theory Sigma Field and MeasuresDocument11 paginiProbability Theory Sigma Field and MeasuresgalaxystarÎncă nu există evaluări
- Estadistica No Parametrica de ConoverDocument225 paginiEstadistica No Parametrica de ConoverEdward William Miranda GutierrezÎncă nu există evaluări
- Statistics - Xii Chapter - 3 Correlation Test MCQ - Marks 30 35 MinDocument5 paginiStatistics - Xii Chapter - 3 Correlation Test MCQ - Marks 30 35 Minapi-232747878Încă nu există evaluări
- Assignment 3Document3 paginiAssignment 3Aaron Wolbrueck100% (3)
- STATS PROBABILITY EXAMDocument3 paginiSTATS PROBABILITY EXAMledan ben NakilaÎncă nu există evaluări
- p1 Formula SheetDocument2 paginip1 Formula SheetAnonymous KktsxF6UpwÎncă nu există evaluări
- Probability Generating FunctionsDocument4 paginiProbability Generating FunctionsKrishan LalÎncă nu există evaluări
- Unit 1 ProblemsDocument7 paginiUnit 1 Problems21ubha116 21ubha116Încă nu există evaluări
- Waiting Time ParadoxDocument9 paginiWaiting Time ParadoxmelanocitosÎncă nu există evaluări
- 11-Introduction To Random variable-27-Jul-2020Material - I - 27-Jul-2020 - Random - Variable - PPTDocument28 pagini11-Introduction To Random variable-27-Jul-2020Material - I - 27-Jul-2020 - Random - Variable - PPTamoghÎncă nu există evaluări
- Probability and Statistics: Dr. Faisal Bukhari Punjab University College of Information Technology (PUCIT)Document26 paginiProbability and Statistics: Dr. Faisal Bukhari Punjab University College of Information Technology (PUCIT)abdullahÎncă nu există evaluări
- Lesson4 MAT284 PDFDocument36 paginiLesson4 MAT284 PDFMayankJain100% (1)
- Levels of measurement and problems involving mean and varianceDocument5 paginiLevels of measurement and problems involving mean and varianceCielo DimayugaÎncă nu există evaluări