STAT 153: Homework 1

Due: September 13, 2016 at 6pm

1 Problem 1
Suppose
k
X
Yt = 0 + [Ai cos(2fi t) + Bi sin(2fi t)] ,
i=1

where 0 , f1 , f2 , ..., fk are constants and A1 , A2 , ..., Ak , B1 , B2 , ..., Bk are independent random variables with zero
means and variances Var(Ai ) = Var(Bi ) = i2 . Show that {Yt } is stationary and find its autocovariance function.

2 Problem 2
Consider the random walk with drift model xt = + xt 1 + wt for t = 1, 2, ..., with x0 = 0, where wt is white noise
2
with variance w and 6= 0.
Pt
(a) Show that the model can be written as xt = t + k=1 wk .
(b) Find the mean function and the autocovariance function of xt .

(c) Argue that xt is not stationary.

q
(d) Show that t 1,t = t t 1 . What happens when t ! 1?

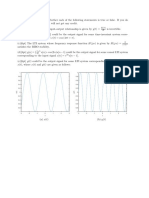
(e) Simulate this process using R for t = 1, ..., 10000, = 1, and w1 , ..., w1000 iid N (0, 4). Create 4 line plots of the
time series xt : (1) only t = 0, 1, ..., 10; (2) only t = 0, 1, ..., 100; (3) only t = 0, 1, ..., 1000; (4) t = 0, 1, ..., 10000.
Explain what you see in the graphs and why it is reasonable to call xt a random walk with drift.

3 Problem 3
Let {et } be a zero-mean white noise process, and let c be a constant with |c| < 1. Define Yt recursively by
Yt = cYt 1 + et with Y1 = e1 .

(a) Show that E(Yt ) = 0.

2
(b) Show that Var(Yt ) = e (1 + c2 + ..., c2t 2
). Is {Yt } stationary?
(c) Show that for k > 0, s
Var(Yt k )
Corr(Yt , Yt k) = ck .
Var(Yt )

(d) For large t, argue that for k > 0

2
e
Var(Yt ) and Corr(Yt , Yt k) ck
1 c2
so that {Yt } could be called asymptotically stationary.
(e) Suppose now that we alter the initial condition and put Y1 = p e1 . Show that now {Yt } is stationary.
1 c2