Radu Serban Algebra

Capitolul 1 Page 1 of 18
CAPITOLUL 1
SPAŢII VECTORIALE
1.1. Noţiunea de spaţiu vectorial
Fie V o mulţime nevidă. Fie (K,+,·) un corp în raport cu operaţiile “+” şi “.”
Elementele corpului K le vom numi scalari sau numere.
Pe mulţimea V introducem legea : ϕ : V × V → V , ϕ ( x, y ) = x ⊕ y care este o
lege de compoziţie internă pe V, iar pe corpul K introducem legea de compoziţie
externă: ψ : K × V → V , ψ (α , x ) = α ⊗ x .
DEFINIŢIA 1.1.1.
Mulţimea nevidă V peste care s-au introdus două operaţii :

ϕ ( x, y ) = x ⊕ y şi ψ (α , x ) = α ⊗ x
prima, internă pe V, cea de-a doua, externă cu valori din K, se numeşte spaţiu vectorial (liniar)
peste corpul K, dacă sunt satisfăcute proprietăţile:
¾ (V ,⊕) formează un grup abelian, adică adunarea este asociativă, are element neutru
θ, are element simetric, şi este comutativă.
¾ 1) 1 ⊗ x = x , oricare ar fi elementul x din V

2) (α + β ) ⊗ x = (α ⊗ x ) + ( β ⊗ x ) , oricare ar fi x şi y din V, α şi β din K
3) (α • β ) ⊗ x = α • ( β ⊗ x ) , oricare ar fi x şi y din V, α şi β din K
4) α ⊗ ( x ⊕ y ) = (α ⊗ x ) ⊕ (α ⊗ y ) , oricare ar fi x şi y din V, α şi β din K
EXEMPLUL 1:
Fie V = Rn spaţiul real n dimensional , iar K = R

Rn = R x R = { ( x1 , x2 , … , xn )T | xi aparţinând lui R, i = 1, … ,n }
⎛ x1 ⎞
⎜ ⎟
⎜x ⎟
x=⎜ 2⎟
Μ
⎜⎜ ⎟⎟
Dacă x aparţine lui Rn , atunci vom nota : ⎝ xn ⎠ = (x1 , x 2 ,Κ , x n )T
⎛ y1 ⎞
⎜ ⎟
⎜y ⎟
y=⎜ 2⎟
Μ
⎜⎜ ⎟⎟
Fie y din spaţiul Rn , ⎝ yn ⎠
file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

⎛ x1 + y 1 ⎞ ⎛ αx1 ⎞
⎜ ⎟ ⎜ ⎟
⎜ x2 + y2 ⎟ ⎜ αx 2 ⎟
x⊕ y =⎜ ⎟ α⊗x=⎜
Μ Μ ⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
Introducem notaţiile: x
⎝ n + y n ⎠ şi αx
⎝ n⎠
Arătăm că ( Rn , R ) este un spaţiu vectorial real , n-dimensional.
¾ 1) asociativitatea rezultă din asociativitatea numerelor reale

⎛0⎞
⎜ ⎟
θ = ⎜⎜ ⎟⎟
0
Μ
⎜⎜ ⎟⎟
2) elementul neutru este ⎝0⎠
⎛ − x1 ⎞
⎜ ⎟
⎜ − x2 ⎟
−x=⎜
Μ ⎟
⎜⎜ ⎟⎟
3) elementul simetric este −
⎝ n⎠x
4) comutativitatea rezultă din comutativitatea adunării numerelor reale
⎛ 1 • x1 ⎞
⎜ ⎟
⎜1 • x 2 ⎟
1⊗ x = ⎜ =x
Μ ⎟
⎜⎜ ⎟⎟
¾ 1) ⎝1 • x n ⎠
⎛ αx1 + βx1 ⎞
⎜ ⎟
⎜ αx2 + βx2 ⎟
(α + β ) ⊗ x = ⎜ ⎟ = (α ⊗ x ) ⊕ ( β ⊗ x )
Μ
⎜⎜ ⎟⎟
2) ⎝ αxn + βxn ⎠
⎛ αx1 ⎞ ⎛ βx1 ⎞ ⎛ αx1 + βx1 ⎞

⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ αx 2 ⎟ ⎜ βx 2 ⎟ ⎜ αx 2 + βx 2 ⎟
α⊗x=⎜ β⊗x=⎜ (α ⊗ x ) ⊕ ( β ⊗ x ) = ⎜
Μ ⎟ Μ ⎟ Μ ⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
3) ⎝ αx n ⎠ ⎝ βx n ⎠ deci ⎝ αx n + βx n ⎠
DEFINIŢIA 1.1.2.
Elementele unui spaţiu vectorial le vom numi vectori.
DEFINIŢIA 1.1.3.
Elementele corpului K le vom numi scalari.
EXEMPLUL 2 :

Fie Pn [x] mulţinea tuturor polinoamelor de gradul n cu coeficienţi reali.

Dacă p aparţine mulţimii Pn [x] , atunci p(x) = a0 + a1 x1 + … + an xn , unde a este
diferit de zero.
Dacă q aparţine mulţimii Pn [x] , atunci q(x) = b0 + b1 x1 + … + bn xn , unde b este
diferit de zero.
( p ⊕ q )( x ) = a 0 + b0 + ( a1 + b1 ) x + Κ + ( a n + bn ) x n
(α ⊗ p )( x ) = αa 0 + αa1 x1 + Κ + αa n x n
Din aceste două relaţii observăm că mulţimea Pn [x] nu formează un spaţiu vectorial
deoarece, dacă avem an = -bn , în urma adunării rezultă un polinom care nu este de gradul n .
Dacă notăm cu Pn [x] mulţimea polinoamelor de grad mai mic sau egal cu n şi
introducem aceste două legi de compoziţie, atunci mulţimea dată formează un spaţiu vectorial.
PROPOZIŢIA 1.1.1.
Fie (V,K) un spaţiu vectorial. Atunci elementul neutru θ este unic.
DEMONSTRAŢIE:
Din propoziţie ştim că există elementul neutru θ, oricare ar fi vectorul x din

mulţimea V. Aceasta înseamnă că θ+x = x+θ = x. Presupunem că există două elemente
neutre θ1 şi θ2. Atunci fiecare din cele două elemente neutre verifică relaţia de mai sus:
θ1+x = x+θ1 = x pentru orice x aparţinând mulţimii V.

θ2+x = x+θ2 = x pentru orice x aparţinând mulţimii V.
Dacă aceste relaţii sunt adevărate pentru orice x aparţinând mulţimii V, atunci sunt
adevărate şi pentru θ care aparţine mulţimii V. Astfel, putem scrie:
pentru x = θ2, θ1+θ2 = θ2+θ1 = θ2

pentru x = θ1 , θ2+θ1 = θ1+θ2 = θ1
Din cele două relaţii observăm că θ1 = θ2, deci elementul neutru este unic.
1.2. Vectori liniar independenţi şi liniar dependenţi; bază şi dimensiune
Fie (V,K) un spaţiu vectorial.

Fie x1, x2, … , xn vectori care aparţin mulţimii V.
Fie λ1, λ2,…, λn scalari care aparţin corpului K.
DEFINIŢIA 1.2.1.

n
λ1 x1 + λ 2 x 2 + Κ + λn x n = ∑ λi x i
Relaţia : i =1
se numeşte combinaţie liniară a vectorilor x1 , x2 , …, xn cu scalari din K.
DEFINIŢIA 1.2.2.
Vectorii x1, x2, …, xn care aparţin mulţimii V se numesc liniar independenţi atunci când
relaţia (1 ) λ1 x1 + λ2 x2 + …+ λn xn = θ este adevărată dacă şi numai dacă toţi scalarii sunt
nuli: λ1 = λ2 = … = λn = 0.
DEFINIŢIA 1.2.3.
Dacă relaţia (1) are loc fără ca toţi scalarii λ1 , λ2 , … , λn să fie nuli,vectorii x1 , x2 , … ,
xn se numesc liniar dependenţi.
EXEMPLUL 1:
Fie ( R3 , R ) un spaţiu vectorial , fie x1 , x2 , x3 vectori din acest spaţiu

⎛1 ⎞ ⎛1 ⎞ ⎛0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
x1 = ⎜ 1 ⎟ x2 = ⎜ 0 ⎟ x 3 = ⎜1 ⎟
⎜0⎟ ⎜1 ⎟ ⎜1 ⎟
vectorial. ⎝ ⎠ , ⎝ ⎠ , ⎝ ⎠
Să se arate că aceşti vectori sunt liniar independenţi.
λ1 x1 + λ2 x2 + …+ λn xn = θ
⎛1 ⎞ ⎛1 ⎞ ⎛ 0⎞ ⎛ 0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
λ1 ⎜1 ⎟ + λ2 ⎜ 0 ⎟ + λ3 ⎜1 ⎟ = ⎜ 0 ⎟
⎜0⎟ ⎜1 ⎟ ⎜1 ⎟ ⎜ 0 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎧λ1 + λ2 = 0 1 1 0 1 1 0
⎪
⎨λ1 + λ3 = 0 1 0 1 = 0 −1 1
⎪λ + λ = 0
⎩ 2 3 0 1 1 0 1 1 = -2 întrucât determinantul este diferit de zero,
soluţia sistemului este λ1 = λ2 = λ3 = 0 , deci vectorii x1 , x2 , x3 sunt liniar independenţi.
PROPOZIŢIA 1.2.1.
Fie (V,K) un spaţiu vectorial. Vectorii x1 , x2 , … , xn sunt liniar dependenţi dacă şi numai
dacă cel puţin un vector este o combinaţie liniară a celorlalţi vectori.
DEMONSTRAŢIE:
1* Presupunem că x1 , x2 , … , xk-1 , xk , xk+1 , …, xn sunt liniar dependenţi şi vom

demonstra că cel puţin un vector este o combinaţie liniară a celorlalţi. Vectorii fiind liniar
independenţi, înseamnă că relaţia :
λ1 x1 + λ2 x2 + … + λk-1 xk-1 + λk xk + λk+1 xk+1 + … + λk xk = θ este adevărată fără ca
toţi scalarii să fie nuli.

Presupunem că λ k este diferit de zero. Atunci:
⎛λ λ λ λ λ ⎞ n
λ
x k = −⎜⎜ 1 x1 + 2 x 2 + Κ + k −1 x k −1 + k +1 x k + Κ + n x n ⎟⎟ = − ∑ i x i
⎝ λk λk λk λk λk ⎠ i =1 λ k
i ≠k
2* Presupunem că cel puţin un vector este o combinaţie liniară a celorlalţi vectori şi

vom demonstra că vectorii sunt liniar dependenţi.
xk = α1 x1 + α2 x2 + … + αk-1 xk-1 + αk xk + αk+1 xk+1 + … + αn xn
α1 x1 + α2 x2 + … + αk-1 xk-1 + (-1) xk + αk+1 xk+1 + … + αn xn = θ
Întrucât (-1) este un scalar diferit de zero, ultima relaţie demonstrează că vectorii sunt liniar
dependenţi.
DEFINIŢIA 1.2.4.
Vectorii x1 , x2 , … , xn care aparţin mulţimii V formează un sistem de generatori ai

spaţiului V, dacă oricare ar fi vectorul x din mulţimea V, există scalarii λ1 , λ2 , … , λn aparţinând
corpului K astfel încât să existe relaţia:
x = λ1 x1 + λ2 x2 + … + λn xn (3)
Altfel spus, x1 , x2, …, xn formează un sistem de generatori dacă oricare ar fi

vectorul x din mulţimea V, el se poate scrie ca o combinaţie liniară a vectorilor x1 , x2 , … ,
xn .
DEFINIŢIA 1.2.5.
Fie (V,K) un spaţiu vectorial. Vectorii x1 , x2 , … , xn formează o bază a spaţiului V dacă

sunt îndeplinite următoarele condiţii:
1) vectorii x1 , x2 , … , xn formează un sistem de generatori.
2) vectorii x1 , x2 , … , xn sunt liniar independenţi.
EXEMPLUL 2 :
Fie ( R3 , R ) un spaţiu vectorial , fie x1 , x2 , x3 vectori din acest spaţiu

⎛1 ⎞ ⎛1 ⎞ ⎛0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
x1 = ⎜ 1 ⎟ x2 = ⎜ 0 ⎟ x 3 = ⎜1 ⎟
⎜0⎟ ⎜1 ⎟ ⎜1 ⎟
vectorial. ⎝ ⎠ , ⎝ ⎠ , ⎝ ⎠
În exemplul anterior am arătat că aceşti vectori sunt liniar independenţi. În continuare
vom arăta că formează un sistem de generatori.
Ştim că oricare ar fi vectorul x din R3 , există scalarii λ1 , λ2 , λ3 astfel încât x = λ1

⎛ x1 ⎞
⎜ ⎟
x = ⎜ x2 ⎟
⎜x ⎟
x1 + λ2 x2 + λ3 x3 , ⎝ 3⎠
⎛1 ⎞ ⎛1 ⎞ ⎛ 0⎞ ⎛ x1 ⎞ ⎧λ1 + λ2 = x1
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎪
λ1 ⎜1 ⎟ + λ2 ⎜ 0 ⎟ + λ3 ⎜1 ⎟ = x = ⎜ x 2 ⎟ ⎨λ1 + λ3 = x 2
⎜ 0⎟ ⎜1 ⎟ ⎜1 ⎟ ⎜x ⎟ ⎪λ + λ = x
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ 3⎠ deci sistemul ⎩ 2 3 3 este un sistem
liniar, neomogen. Vectorii x1 , x2 , x3 formează un sistem de generatori deoarece sistemul de

mai sus este compatibil determinat.
Astfel am demonstrat că vectorii x1 , x2 , x3 formează o bază în R3 .
DEFINIŢIA 1.2.6.
Dimensiunea spaţiului vectorial V este egală cu numărul vectorilor unei baze.
PROPOZIŢIA 1.2.2.
Fie V un spaţiu vectorial peste corpul K , dimensiunea spaţiului V fiind n.

Fie B = { x1 , x2 , … , xn } o bază în spaţiul V.
Atunci, oricare ar fi vectorul x din V el se scrie în mod unic ca o combinaţie liniară de
vectorii bazei.
DEMONSTRAŢIE:
Din ipoteză ştim că B = { x1 , x2 , … , xn } este o bază. Aceasta înseamnă că vectorii x1 ,

x2 , … , xn formează un sistem de generatori şi sunt liniar independenţi.
Intrucât vectorii x1 , x2 , … , xn formează un sistem de generatori , înseamnă că este
verificată relaţia:
x = λ1 x1 + λ2 x2 + … + λn xn (1)
Presupunem că x se scrie şi sub forma: x = β1x1 + β2x2 + … + βnxn (2)

Înmulţind relaţia (2) cu -1 şi adunând-o cu relaţia (1) vom obţine:
x + (-x) = ( α1 – β1) x1 + ( α2 – β2 ) x2 + … + ( αn – βn) xn = θ
Din această relaţie şi din faptul că vectorii subt liniar independenţi, rezultă că:
α1 – β1 = 0, α2 – β2 = 0, … , αn – βn = 0 , adică α1= β1, α2 = β2, … , α3 = β3.
V este un spaţiu vectorial de dimensiune n , iar B = { x1, x2, … , xn } este o bază în V.

Atunci, oricare ar fi vectorul x din V, el se scrie în mod unic sub forma unei combinaţii liniare
de vectorii bazei. Deci x se scrie sub forma:
x = α1 x1 + α2 x2 + … + αn xn .

DEFINIŢIA 1.2.7.
Scalarii α1 , α2 , … , αn se numesc coordonatele vectorului x în baza B.

⎛ α1 ⎞
⎜ ⎟
⎜α ⎟
xB = ⎜ 2 ⎟
Μ
⎜⎜ ⎟⎟
⎝α n ⎠
EXEMPLUL 1:
Fie P2 [x] spaţiul vectorial al polinoamelor de grad mai mic sau egal cu 2, cu coeficienţi
reali. Să se cerceteze dacă vectorii B1 = { 1 + x , 1 + x2 , x + x2 } şi B2 = { 1 + 2x + 2x2 }
formează sau nu o bază.
(i) Oricare ar fi polinomul p din spaţiul vectorial P2 [x], p(x) = a0 + a1x + +a2 x2,
unde a, a, a sunt numere reale, există λ1 , λ2 , λ3 astfel încât p = λ1 p1 + λ2 p2 +λ3 p3
λ1 ( 1+x) + λ2 (1 + x2 ) + λ3 ( x + x2) = a0 + a1 x + a2 x2
( λ1 + λ2) + ( λ1 + λ3) x + ( λ2 + λ3) x2 = a0 + a1 x + a2 x2
Din aceste două relaţii obţinem un sistem compatibil determinat:
⎧λ1 + λ2 = a 0
⎪
⎨λ1 + λ3 = a1
⎪λ + λ = a
⎩ 2 3 2
(ii) Vectorii sunt liniar independenţi : θ = 0 + 0x + 0x2
⎧λ1 + λ2 = 0
⎪
⎨λ1 + λ3 = 0
⎪λ + λ = 0
⎩ 2 3
1.3. Schimbarea coordonatelor unui vector la schimbarea bazelor
Fie (V,K) un spaţiu vectorial de dimensiune n.

Fie E = { e1 , e2 , … , en } o bază în spaţiul vectorial V.
Fie x un vector din V , xE = α1 e1 + α2 e2 + … + αn en , xE = ( α1 , α2 , … , αn )T
Fie G = { g1 , g2 , … , gn } o altă bază în spaţiul vectorial V.
xG = β1 g1 + β2 g2 + … + βn gn , xG = ( β1 , β2 , … , βn )T
Deoarece E şi G formează baze în spaţiul V, înseamnă că vectorii ei şi gi aparţin spaţiului V

oricare ar fi indicele “i” cu valori în mulţimea { 1, … , n }.

g1 aparţine lui V, atunci g1 = c11 e1 + c12 e2 + … + c1n en

g2 aparţine lui V, atunci g2 = c21 e1 + c22 e2 + … + c2n en
…………………………………………………………………………………………..
gn aparţine lui V, atunci gn = cn1 e1 + cn2 e2 + … + cnn en
Vom nota cu CEG = (cij ) , unde cij aparţine corpului K, iar indicii i şi j aparţin mulţimii { 1 ,
… , n }.
DEFINIŢIA 1.3.1.
Matricea CEG = (cij ) se numeşte matricea de trecere de la baza E la baza G.
OBSERVAŢIE : Determinantul matricei CEG este diferit de zero, ceea ce înseamnă că

matricea este nesingulară.
PROPOZIŢIA 1.3.1.
Fie (V,K ) un spaţiu vectorial de dimensiune n .

Fie E şi G două baze în spaţiul V, E = { e1 , e2 , … , en } , G = { g1 , g2 , … , gn }
Fie vectorul x din V, xE = ( α1 , α2 , … , αn )T şi xG = ( β1 , β2 , … , βn )T
xE = α1 e1 + α2 e2 + … + αn en
xG = β1 g1 + β2 g2 + … + βn gn
Atunci este adevărată relaţia: XG = ( CT EG )-1 XE
DEMONSTRAŢIE:
gi = ci1 e1 + ci2 e2 + … + cin en =

xG = β1 g1 + β2 g2 + … + βn gn = β1 (c11 e1 + c12 e2 + … + c1n en ) +
+ β2 (c21 e1 + c22 e2 + … + c2n en ) +
+ …………………………………+
+ βn (cn1 e1 + cn2 e2 + … + cnn en ) =
= ( β1 c11 + β2 c21 + … + βn cn1 ) e1 + ( β1 c12 + β2 c22 + … + βn cn2 ) e2 + … +
+ ( β1 c1n + β2 c2n + … + βn cnn ) en
Deoarece scrierea unui vector într-o bază este unică, vom obţine:
⎧ β 1 c11 + β 2 c 21 + Κ + β n c n1 = α 1
⎪β c + β c + Κ + β c = α
⎪ 1 12 2 22 n n2 2
⎨
⎪Μ
⎪⎩ β 1 c1n + β 2 c 2 n + Κ + β n c nn = α n
Acest sistem, scris matriceal, are forma : CT EG XG = XE ( 2’ )

Determinantul matricei CEG este diferit de zero, deci şi determinantul matricei CTEG este
diferit de zero, astfel încât există ( CT EG )-1

Din ( 2’ ) obţinem:
( CT EG )-1 CT EG XG = ( CT EG )-1 XE , adică , XG = ( CT EG )-1 XE
1.4. Lema substituţiei
Fie (V,K) un spaţiu vectorial de dimensiune n .

Fie E = { e1 , e2 , … , en } = { e1 , e2, … , ei-1 , ei , ei+1 , … , en } o bază în spaţiul V.
Fie u un vector oarecare din V, uE = ( λ1 , λ2 , … , λi-1 , λi , λi+1 , … , λn )T
uE = λ1 e1 + λ2 e2 + … + λi-1 ei-1 + λi ei + λi+1 ei+1 + … + λn en
Lema substituţiei răspunde la următoarele întrebări:
1) În ce condiţii mulţimea E* = { e1 , e2 , … , ei-1 , u , ei+1 , … , en } formează o bază în

spaţiul V ?
2) Fiind dat un vector x din spaţiul V , xE = ( α1 , α2 , … , αi-1 , αi , αi+1 , … , αn )T , care sunt
coordonatele vectorului în baza E* ?
xE * = ( α *1 , α *2 , … , α *i-1 , α *i , α *i+1 , … , α *n )T
Vom demonstra că mulţimea E* = { e1 , e2 , … , ei-1 , u , ei+1 , … , en } formează o bază şi că

dacă vectorul x aparţine spaţiului V, xE = ( α1 , α2 , … , αi-1 , αi , αi+1 , … , αn )T şi dacă xE * =
( α *1 , α *2 , … , α *i-1 , α *i , α *i+1 , … , α *n )T, atunci:
αi α j λi − α i λ j
α i* = α *j =
(1) λi ; (2) λi unde j ia valori din mulţimea { 1 , … , n }, j fiind
diferit de i .
DEMONSTRAŢIE:
1) Trebuie să arătăm că vectorii { e1 , e2 , … , ei-1 , u , ei+1 , … , en } sunt liniar independenţi .

µ1 e1 + µ2 e2 + … + µi-1 ei-1 + µi u + µi+1 ei+1 + … + µn en = θ
µ1 e1 + µ2 e2 + … + µi-1 ei-1 + µi ( λ1 e1 + λ2 e2 + … + λi-1 ei-1 + λi ei + λi+1 ei+1 + …+λnen)+
+µi+1 ei+1 + … + µn en = θ
( µ1 +µi λ1 ) e1 + … + ( µi-1 + µi λi-1 ) ei-1 + µi λi ei + ( µi λi+1 + µi+1 ) ei+1 + … + ( µi λn + + µn )
en = θ
Dar vectorii { e1 , e2 , … , en } formează o bază deci sunt liniar independenţi. Astfel, obţinem
un sistem liniar şi omogen de n ecuaţii şi n necunoscute:

⎧µ1 + µ i λ1 = 0 1 Κ Κ 0 λ1 0 Κ Κ 0
⎪Μ ΜΚ Κ Κ Κ Κ Κ Κ Μ
⎪
⎪µ i −1 + µ i λi −1 = 0 0 Κ Κ 1 λi −1 0 Κ Κ 0
⎪
⎨ µ i λi = 0 A= 0 Κ Κ 0 λi 1 Κ Κ 0
⎪µ λ + µ = 0 0 Κ Κ 0 λi +1 1 Κ Κ 0
⎪ i i +1 i +1
⎪Μ ΜΚ Κ Κ Κ Κ Κ Κ Μ
⎪
(3) ⎩µ i λn + µ n = 0 0 Κ Κ 0 λn 0 Κ Κ 0
Determinantul sistemului este: detA = (-1)i+1 λi | Ii-1 | , deci detA = λi şi este diferit de zero.
Înseamnă că sistemul (3) are numai soluţia banală.
Deci vectorii { e1, e2, … , ei-1, u , ei+1, … , en } sunt liniar independenţi .
2) Trebuie să arătăm că { e1, e2, … , ei-1, u , ei+1, … , en } formează un sistem de generatori.

Oricare ar fi vectorul x din spaţiul V, există scalarii α *1 , α *2 , … , α *i-1 , α *i , α
* , … , α *n astfel încât
i+1
xE = λ*1 e1 + λ*2 e2 + … + λ*i-1 ei-1 + λ*i u + λ*i+1 ei+1 + … + λ*n en
xE = λ*1 e1 + λ*2 e2 + … + λ*i-1 ei-1 + λ*i (λ1 e1 + λ2 e2 + … + λi-1 ei-1 + λi ei + λi+1 ei+1 + …+ +λn
en ) + λ*i+1 ei+1 + …+ λ*n en = ( α*1 + α*i λ1 ) e1 + …+ ( α*i-1 + α*i λi-1 ) ei-1 + α*i λi ei +
+( α*i+1 + α*i λi+1 ) ei+1 + ( α*n + α*i λn ) en
Ştim că scrierea unui vector într-o bază este unică. Vom obţine sistemul:
⎧α 1* + α i* λ1 = α 1
⎪
⎪Κ Κ Κ Κ Κ Κ Κ
⎪α * + α * λ = α
⎪⎪ i*−1 i i −1 i −1
⎨α i λi = α i
⎪α * + α * λ = α
⎪ i +1 i i +1 i +1
⎪Κ Κ Κ Κ Κ Κ Κ αi
⎪ * α i* =
⎪⎩α n + α i λn = α n
*
rezultă că λi
Celelalte ecuaţii le putem scrie sub forma:
α *j + α i* λ j = α j
αiλ j α j λi − α i λ j
α *j = α j − α i* λ j = α j − α *j =
λi
de aici rezultă că λi pentru
oricare j din mulţimea { 1, … , n } , j fiind diferit de i.
Formulele ( 1 ) şi ( 2 ) se numesc formulele de pivotare Gauss- Jordan.

E U X E* X
e1 λ1 α1 e1 α*1
· · · · ·
· · · · ·
· · · · ·
ei-1 λi-1 αi-1 ei-1 *
α i-1
ei λi αi u α*i
ei+1 λi+1 αi+1 ei+1 α*i+1
· · · · ·
· · · · ·
· · · · ·
ej λj αj ej α*j
· · · · ·
· · · · ·
en λn αn e1 α*n
( 1 ) Se împarte linia pivot la pivot ; ( 2 ) Se aplică Gauss-Jordan.
1.5. Spaţii vectoriale izomorfe
Fie (X,K) şi (Y,K) două spaţii vectoriale peste acelaşi corp de sclari K.
DEFINIŢA 1.5.1.
Spaţiile vectoriale X şi Y se numesc K izomorfe, dacă există φ : X→ Y cu proprietăţile

următoare: 1) φ este bijectivă
2) oricare ar fi x1 şi x2 doi vectori din spaţiul X şi oricare ar fi α1 şi α2
scalari din corpul K, atunci φ ( α1 x1 + α2 x2 ) = α1 φ ( x1 ) + α2 φ ( x2 ) .
Funcţia φ cu proprietatea 2) se numeşte aplicaţie sau funcţie liniară.
TEOREMA 1.5.1.
Dacă X şi Y sunt două spaţii vectoriale definite pe acelaşi corp de scalari K, dimensiunea
celor două spaţii fiind n finit, atunci X şi Y sunt K-izomorfe.
Aceasta este teorema de izomorfism a spaţiilor vectoriale finit dimensionale.
DEMONSTRAŢIE:
Fie E = { e1 , e2 , … , en } o bază în spaţiul X

Fie G = { g1 , g2 , … , gn } o bază în spaţiul Y
n
Oricare ar fi vectorul x din spaţiul X, x = α1 e1 + α2 e2 + … + αn en =

∑α e
i =1
i i
n n
ϕ ( ∑ α i ei ) = ∑ α i g i
Definesc funcţia φ : X → Y, φ ( x ) = y i =1 i =1

Pentru a arăta că φ este izomorfism, demonstrăm că:

1) funcţia este bijectivă:
* injectivitate: oricare ar fi x1 şi x2, x1 diferit de x2, atunci φ ( x1 ) este diferit de φ
( x2 ) .
Fie x1 = α1 e1 + α2 e2 + … + αk ek + … + αn en
Fie x2 = β1 e1 + β2 e2 + … + βk ek + … + βn en unde αi şi βi aparţin corpului K, oricare ar
fi indicele “i” din mulţimea { 1, … , k , … , n } .
Întrucât x1 este diferit de x2 , există cel puţin un indice “k” din mulţimea { 1, … , n } astfel
încât αk este diferit de βk .
φ ( x1 ) = α1 e1 + α2 e2 + … + αk ek + … + αn en
φ ( x2 ) = β1 e1 + β2 e2 + … + βk ek + … + βn en
Deoarece există cel puţin un indice “k” din mulţimea { 1, … , n } astfel încât αk este diferit de
βk , atunci φ ( x1 ) este diferit de φ ( x2 ).
* surjectivitate: oricare ar fi y din Y, există x din X astfel încât φ ( x ) = y.

Oricare ar fi y din Y, există scalarii α1 , α2 , … , αn din corpul K astfel încât să
existe relaţia: y = α1 g1 + α2 g2 + … + αn gn . Considerăm un x care aparţine lui X,
x = α1 e1 + α2 e2 + … + αn en . Din definiţia funcţiei φ rezultă că φ ( x ) = y.
2) liniaritatea funcţiei φ :
Oricare ar fi x1 şi x2 din spaţiul X şi oricare ar fi a şi b din corpul K,
φ ( a x1 + b x2 ) = a φ ( x1 ) + b φ ( x2 )
n n
x1 = ∑ α i e i x 2 = ∑ β i ei
i =1 i =1 , unde αi , βi aparţin corpului K, iar i aparţine mulţimii { 1 , … , n}
⎡ n n
⎤ ⎡ n
⎤ n
ϕ (ax1 + bx 2 ) = ϕ ⎢a ∑ α i ei + b∑ β i ei ⎥ = ϕ ⎢∑ (aα i + bβ i )ei ⎥ = ∑ (aα i + bβ i )g i =
⎣ i =1 i =1 ⎦ ⎣ i =1 ⎦ i =1
n n n n
= ∑ aα i g i + ∑ bβ i g i = a ∑ α i g i + b∑ β i g i = aϕ ( x1 ) + bϕ ( x 2 )
i =1 i =1 i =1 i =1
1.6. Subspaţii liniare
Fie (X,K) un spaţiu liniar vectorial; fie X0 un spatiu inclus în spaţiul X, X0 fiind diferit
de mulţimea vidă.
DEFINIŢIA 1.6.1.
Mulţimea X0 este un subspaţiu liniar al spaţiului X dacă:

1) oricare ar fi x, y doi vectori din X0 , atunci şi x + y aparţine lui X0 .
2) oricare ar fi scalarul α din corpul K şi oricare ar fi vectorul x din X0 şi α x

aparţine lui X0 .
PROPOZIŢIA 1.6.1.
Dacă Xi ( i aparţine unei familii de indici ) este o familie de subspaţii liniare a spaţiului
liniar ( X,K ) , atunci şi mulţimea X0 formată din intersecţia subspaţiilor Xi este un subspaţiu
liniar al spaţiului X.
DEMONSTRAŢIE:
Ι X i , x aparţine lui X şi y
1) oricare ar fi vectorii x şi y din spaţiul X0 , X0 = i∈I i
aparţine lui Xi , pentru orice i din I .
Dar Xi este un subspaţiu liniar al lui X, deci x+y aparţin lui Xi oricare ar fi i din
mulţimea I, adică x+y aparţin lui X0 .
2) Oricare ar fi vectorul x din spaţiul X0 , x aparţine subspaţiului Xi al spaţiului X0 . Oricare

ar fi scalarul α din corpul K, αx aparţine spaţiului Xi , deci aparţine şi subspaţiului X0.
Fie (X,K) un spaţiu liniar. Fie mulţimea A ⊂ X , A ≠ ∅ .
DEFINIŢIA 1.6.2.
Se numeşte acoperirea liniară a mulţimii A, mulţimea tuturor combinaţiilor liniare de

vectori din mulţimea A . Acoperirea liniară se notează cu L(A).
⎧ p
⎫
⎨
L(A) = ⎩
x | x = ∑ α i a i , a i ∈ A, α i ∈ K , i = 1, Κ , p, p ∈ N * ⎬
i =1 ⎭
PROPOZIŢIA 1.6.2.
Fie (X,K) un spaţiu vectorial. Fie A o mulţime din X, diferită de mulţimea vidă. Atunci
acoperirea liniară a lui A este un subspaţiu liniar al spatiului X.
DEMONSTRAŢIE:
1) Demonstrăm că oricare ar fi vectorii x şi y din L(A) şi x+y aparţine

acoperirii liniare L(A).
Dacă x ∈ L(A), atunci :
p1
x = ∑α i a i
i =1 unde αi este un scalar din K, ai este un vector din A, i = 1, … , p1 , iar p1 este
un număr natural.
Dacă y ∈ L(A), atunci :
p2
y = ∑ β ja j
i =1 unde βj este un scalar din K, aj este un vector din A, j = 1, … , p2 ,
iar p2 este un număr natural.

p1 p2
x + y = ∑α i a i + ∑ β j a j
i =1 deci (x+y) este o combimaţie liniară de vectori din mulţimea
i =1
A, ceea ce înseamnă că (x+y) aparţine acoperirii liniare a mulţimii A.
2) Demonstrăm că oricare ar fi vectorul x din L(A) şi αx aparţine acoperirii

liniare L(A), unde α este un scalar din corpul K.
Dacă x ∈ L(A), atunci :
p1
αx = ∑ (αα i )a i
i =1 oricare ar fi α din corpul K.
Deoarece α i aparţine corpului K şi αα i aparţine corpului K. Rezultă astfel că αx aparţine
acoperirii liniare L(A) .
PROPOZIŢIA 1.6.3.
Fie A o mulţime din spaţiul liniar X, A fiind diferită de mulţimea vidă.

Acoperirea liniară a unei mulţimi conţine mulţimea respectivă.
DEMONSTRAŢIE:
Oricare ar fi elementul a din mulţimea A, el se poate scrie astfel:

1
a = ∑1 * a = 1 * a = a
i =1 aceasta fiind o combinaţie liniară ce aparţine acoperirii
liniare L(A) .
Fie (X,K) un spaţiu liniar şi fie A o mulţime din acest spaţiu, A fiind diferită de mulţimea
vidă.
DEFINIŢIA 1.6.2.
Se numeşte subspaţiu liniar generat de mulţimea A, cel mai mic subspaţiu liniar al
spaţiului X care conţine mulţimea A.
Subspaţiul liniar generat de mulţimea este un subspaţiu al spaţiului X care conţine pe A şi este
cel mai mic subspaţiu care are acestă proprietate. Îl vom nota cu Sp(A).
OBSERVAŢIE: Dacă XA = { Xi | Xi fiind subspaţii ale lui X, A ⊂ X, i = I } , atunci mulţimea

XA este diferită de mulţimea vidă.
PROPOZIŢIA 1.6.4.
Fie (X,K) un spaţiu liniar şi fie A o mulţime inclusă în X, A fiind diferită de mulţimea vidă.
Atunci L(A) = Sp(A) .
DEMONSTRAŢIE:
1) Sp ( A) ⊂ L( A) este evidentă deoarece L(A) este un subspaţiu liniar al lui X care

conţine mulţimea A, iar Sp(A) este cel mai mic subspaţiu cu această proprietate.
2) L( A) ⊂ Sp ( A)

p
x = ∑α k a k
Fie x un vector din L(A) , k =1 , αk aparţinând corpului K şi ak aparţinând mulţimii A ,
k = 1, … ,p .
A ⊂ X i , iar X este un subspaţiu , deci a aparţine subspaţiului X , k = 1, … ,p .

i k i
p
x = ∑α k a k
k =1 aparţine subspaţiului Xi , oricare ar fi Xi care include mulţimea A.
p
Deci
x = ∑α k a k
aparţine
Ι X i = Sp( A)
. Astfel rezultă că L(A) = Sp(A) .
k =1 Xi ⊃ A
PROPOZIŢIA 1.6.5.
Fie (X,K) un spaţiu liniar, fie A o mulţime din X, A fiind diferită de mulţimea vidă. Fie B o
familie maximală de vectori liliar independenţi conţinută în mulţimea A. Atunci, L(A) = L(B) .
OBSERVAŢIE : Fie (X,K) un spaţiu liniar şi fie X0 un subspaţiu liniar al spaţiului X. Atunci
elementul neutru θ aparţine subspaţiului X0 .
DEMONSTRAŢIE :
1) L( A) ⊂ L( B )
Dacă B este o familie maximală de vectori liniar independenţi din mulţimea A, atunci oricare
ar fi elementul a din A, a este o combinaţie liniară de elemente din familia maximală B. Rezultă
că oricare ar fi vectorul x aparţinând acoperirii liniare L(A), x este o combinaţie liniară de
elemente din B, adică x aparţine acoperirii liniare L(B). Deci L( A) ⊂ L( B ) .
2) L( B ) ⊂ L( A) este evidentă.
PROPOZIŢIA 1.6.6.
Fie (X,K) un spaţiu liniar a cărui dimensiune este n. Fie X1 şi X2 două subspaţii liniare ale
lui X.
Dacă dim X1 + dim X2 > dim X , atunci X 1 ∩ X 2 conţine şi alte elemente diferite de θ .
DEMONSTRAŢIE:
Fie dim X1 = p1 . Fie E = { e1 , … , ep } o bază în X1 .

Fie dim X2 = p2 . Fie G = { g1 , … , g2 } o bază în X2 .
p1
x = ∑ α i ei
Dacă x ∈ X1 ∩ X 2 , atunci : i =1 dacă x aparţine subspaţiului X1
p2
x = ∑β jg j
i =1 dacă x aparţine subspaţiului X2

p1 p2 p1 p2
∑ α e = ∑ β g ⇔ ∑ α e + ∑ (− β )g = θ
i =1
i i
j =1
j j
i =1
i i
i =1
j j
Dar {e , Κ , e , g , Κ , g } este o mulţime care aparţine lui X şi are p1 + p2 elemente.

1 p1 1 p2
Din ipoteză ştim că p1 + p2 > p deci vectorii {e , Κ , e , g , Κ , g } sunt liniar dependenţi.

1 p1 1 p2
Presupunem că αi = 0 ( i = 1, … , p1 ) . Atunci există scalari βj diferiţi de zero pentru că

vectorii sunt liniar dependenţi. Presupunem că βj = 0 (j = 1, … , p2 ) . Atunci există scalari αi
diferiţi de zero pentru că vectorii sunt liniar dependenţi. Deci există şi vectori nenuli.
1.7. Sumă de subspaţii liniare
Fie (X,K) un spaţiu liniar . Fie X1 şi X2 două subspaţii liniare ale lui X.
DEFINIŢIA 1.7.1.
Se numeşte suma subspaţiilor X1 şi X2 mulţimea: S = X1 + X2 unde

X1 + X2 = { x | x = x1 + x2 , x1 ∈ X1 , x2 ∈ X2 }.
PROPOZIŢIA 1.7.1.
Suma a două subspaţii liniare este un subspaţiu liniar.
DEMONSTRAŢIE:
1) Oricare ar fi x din S , x = x1 + x2 , x1 ∈ X1 , x2 ∈ X2
Oricare ar fi y din S , y = y1 + y2 , y1 ∈ X1 , y2 ∈ X2
Dacă x1 ∈ X1 şi y1 ∈ X1 , atunci x1 + y1 ∈ X1 .
Dacă x2 ∈ X2 şi y2 ∈ X2 , atunci x2 + y2 ∈ X2 .
x + y = x1 + x2 + y1 + y2 = x1 + y1 + x2 + y2 ∈ S.
2) Oricare ar fi λ un scalar din corpul K, oricare ar fi vectorul x din S, obţinem:

λx = λ(x1 + x2 ) = λx1 + λx2 deci λx ∈ S .
OBSERVAŢIE : 1) În general, X 1 ∪ X 2 nu este un subspaţiu liniar

2) S = X1 + X2 ≠ X 1 ∪ X 2 .
TEOREMA 1.7.1. ( teorema dimensiunii )
Fie (X,K) un spaţiu vectorial de dimensiune n. Fie X1 un subspaţiu liniar, dim X1 = p1 .

Fie X2 un alt subspaţiu al lui X, dim X2 = p2 . Fie D = X1 ∩ X 2 ,dim D = d . Fie S = X1 + X2 , dim S
= s. Atunci :
dim X1 + dim X2 = dim D + dim S ⇔ p1 + p2 = d + s .
DEMONSTRAŢIE :
Fie { e1 , … , ed } o bază în D. Completăm această bază astfel încât să obţinem nişte baze
în X1 şi în X2 .

Fie { e1 , … , ed , fd+1 , … , fp1 } o bază în X1 .

Fie { e1 , … , ed , gd+1 , … , gp2 } o bază în X2 .
Vom arăta că mulţimea BS = { e1 , … , ed , fd+1 , … , fp1 , gd+1 , … , gp2 } formează o bază în S.
1) oricare ar fi x ∈ S, x = x1 + x2 , x1 ∈ X1 , x2 ∈ X2
d p1
x1 = ∑ α i e i + ∑α i fi
Dacă x1 ∈ X1 , atunci i =1 i = d +1
d p2
x 2 = ∑ β i ei + ∑β g i i
Dacă x2 ∈ X2 , atunci i =1 i = d +1
d p1 p2
x = ∑ (α i + β i )ei + ∑ αi fi + ∑β g i i
x∈S , i =1 i = d +1 i = d +1 deci x se scrie ca o combinaţie liniară a
vectorilor din BS . Înseamnă că BS formează un sistem de generatori.
2) arătăm că vectorii din BS sunt liniar independenţi.

p1
∑ (− β ) f
d p2
d p1 p2 j j ∑α e i i + ∑γ k gk
(*)
∑ α i ei +
i =1
∑
j = d +1
βj fj + ∑ γ k g k = θ ⇒ 1j =d4+41 2 4 43
k = d +1 +
1i =1 4 44 2 k4= d +41 43
este vector este vector în X2 ,

în X1 , deci deci x ∈ X2
x ∈ X1
Din cele scrise mai sus, rezultă că x ∈ D = X1 ∩ X 2 , deci γk = 0 ( 1 ) , oricare ar fi k = d+1,

… , p1 .
p2 d p1
∑ (− γ )g k k ∑ α i ei + fj ∑β j
1 44 2 4 43
k = d +1
1 4 4 4 2 4 4 43
i =1 j = d +1
Din ( * ) obţinem : =
x∈ X2 x∈ X1
De aici rezultă că x ∈ X 1 ∩ X 2 , deci βj = 0 ( 2 ) , oricare ar fi j = 1, … , p1 .
d
∑ α i ei = θ
Din ( * ) , ( 1 ) , ( 2 ) obţinem : i =1
Dar vectorii { e1 , … , ed } formează o bază în D, deci sunt liniar independenţi. Rezultă că αi =
0 , oricare ar fi i = 1 , … , d , ceea ce înseamnă că BS formează o bază.
BS are d + p1 – d + p2 – d = s vectori ⇒ -d + p1 + p2 = s ⇒ p1 + p2 = s + d .
COROLAR: Fie S un subspaţiu al spaţiului X , S ⊂ X , deci s ≤ n , atunci:

p1 + p2 – d ≤ n .
OBSERVAŢIE : Dacă X 1 ∩ X 2 = {θ } , atunci d = 0 , p1 + p2 = s , ceea ce inseamnă:

dim X1 + dim X2 = dim ( X1 + X2 ) .
DEFINIŢIA 1.7.2.
Fie X1 şi X2 două subspaţii ale spaţiului (X,K) . Dacă X 1 ∩ X 2 = {θ } , atunci X 1 ⊕ X 2 se

numeşte suma directă a subspaţiilor X1 şi X2 .

CAPITOLUL 2
FUNCŢIONALE LINIARE
2.1. Noţiunea de funcţională liniară
Fie (X,K) un spaţiu vectorial de dimensiune n .
DEFINIŢIA 2.1.1.
O aplicaţie f : X → K , se numeşte funcţională .
DEFINIŢIA 2.1.2.
Funcţionala f : X → K este liniară dacă:

1) oricare ar fi vectorii x şi y din X, f ( x + y ) = f ( x ) + f ( y )
( proprietate de aditivitate)
2) oricare ar fi scalarul λ din corpul K, oricare ar fi vectorul x din X,
f(λx)=λf(x)
( proprietate de omogenitate )
OBSERVAŢIE :
¾ proprietăţile 1) şi 2) pot fi scrise într – o singură formulă :
f ( α x + β b ) = α f ( x ) + β f ( y ) , oricare ar fi scalarii α şi β din corpul K şi
oricare ar fi vectorii x şi y din spaţiul X.
n
⎛ n ⎞ n
x = ∑ α i ei ⇒ f ( x ) = f ⎜ ∑ α i ei ⎟ = ∑ α i f (ei )
¾ Dacă i =1 ⎝ i =1 ⎠ i =1
EXEMPLUL 1 :
Fie spaţiul vectorial ( P2[x], R ) şi fie funcţionala f : P2 [x ] → R, f ( x ) = ∫0 x (t )dt .

1
unde x(t) = a0 + a1 t + a2 t2 , a0 , a1 , a2 ∈ R .
Să se demonstreze că această funciţională este o funcţională liniară.
Oricare ar fi x şi y din ( P2[x], R ) , x(t) = a0 + a1 t + a2 t2 , y(t) = b0 + b1 t + b2 t2 , b0 , b1 , b2

∈R .
Oricare ar fi α şi β din R ,
1
∫0 [αx(t ) + βy (t )]dt = α ∫0 x(t )dt + β ∫ y (t )dt

1 1
f (α x + β y ) = 0 = α f ( x ) +β f ( y ) .
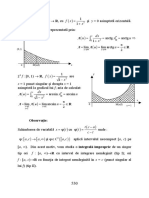
INTERPRETARE GEOMETRICÃ :
Fie spaţiul ( R3, R ) şi fie f : R → R o funcţională liniară.

3

x3
•x R
-e3 |
f(x)
| x1 |
0 e1 f( e3 )
| |
e2 f( e1 )
|
x2 f( e2 )
2.2. Matricea unei funcţionale liniare:
Fie (X,K) un spaţiu vectorial , dim X = n.

Fie E = { e1 , e2 , … , en } o bază în spaţiul X.
Fie x = α1 e1 + α2 e2 + … + αn en , unde x este un vector din X.
Fie f : X → K , o funcţională liniară.
⎛ n ⎞ n
f ( x ) = f ⎜ ∑ α i ei ⎟ = ∑ α i f (ei )
Valoarea funcţionalei în punctul x este: ⎝ i =1 ⎠ i =1 .
Notăm ai = f ( ei ) i = 1, … ,n ( 1 )
DEFINIŢIA 2.2.1
Se numeşte matricea funcţionalei f corespunzătoare bazei E , matricea:

⎛ a1 ⎞
⎜ ⎟
⎜a ⎟
A=⎜ 2 ⎟
Μ
⎜⎜ ⎟⎟
⎝ an ⎠
EXEMPLUL 1 :
f : P2 [x ] → R, f ( x ) = ∫ x (t )dt , o
1
Fie spaţiul vectorial ( P2[x],R ) şi fie funcţionala 0
funcţională liniară. Fie E = { 1, t, t2 } o bază în P2[x] .

Să se determine matricea funcţionalei f în baza E .

a1 = ∫ f (e1 )dt = ∫ 1dt = 1

1 1
0 0
⎛ ⎞
⎜1 ⎟
⎜ ⎟
⎜1⎟
A=⎜ ⎟
2
⎜ ⎟
a 2 = ∫ f (e 2 ) = ∫ tdt =
1 1 1 1
⎜⎜ ⎟⎟
0 0 2 De aici rezultă că ⎝3⎠ .
1
t3
f (e3 )dt = ∫ t dt =
1 1 1
a3 = ∫ 2
=
0 0 3 0
3
2.3. Schimbarea matricei unei funcţionale liniare la schimbarea bazelor
PROPOZIŢIA 2.3.1.
Fie (X,K) un spaţiu vectorial , dim X = n .

Fie E = { e1 , e2 , … , en } o bază în spaţiul X .
n
x = ∑ α i ei
Oricare ar fi vectorul x din spaţiul X , i =1 .
⎛ a1 ⎞
⎜ ⎟
⎜a ⎟
A=⎜ 2⎟
Μ
⎜⎜ ⎟⎟
Fie f : X → K , o funcţională liniară , fie ⎝ a n ⎠ ai = f ( ei ) i = 1, … ,n .
Fie G = { g1 , g2 , … , gn } o altă bază în spaţiul X .
Fie CEG matricea de trecere de la baza E la baza G .
⎛ b1 ⎞
⎜ ⎟
⎜b ⎟
B=⎜ 2⎟
Μ
⎜⎜ ⎟⎟
Fie ⎝ bn ⎠ matricea functionalei f în baza G , bi = f ( gi ) i = 1, … ,n .
Atunci : B = C• A
DEMONSTRAŢIE :
Scriem matricea C ( cij ) , matricea de trecere de la baza E la baza G .
g1 = c11 e1 + c12 e2 + … + c1n en

g2 = c21 e1 + c22 e2 + … + c2n en
………………………………………
gn = cn1 e1 + cn2 e2 + … + cnn en
b1 = f ( g1 ) = c11 f ( e1 ) + c12 f ( e2 ) + … + c1n f ( en )

b2 = f ( g2 ) = c21 f ( e1 ) + c22 f ( e2 ) + … + c2n f ( en )

…………………………………………………………………
bn = f ( gn ) = cn1 f ( e1 ) + c2n f ( e2 ) + … + cnn f ( en )
⎧b1 = c11a1 + c12 a 2 + Κ + c1n a n

⎪
⎨Μ ⇒
⎪b = c a + c a + Κ + c a
sau : ⎩ n n1 1 n2 2 nn n B = C• A
2.4. Dualul algebric al unui spaţiu vectorial
Fie (X,K) un spaţiu vectorial, dim X = n .

Considerăm mulţimea tuturor funcţionalelor liniare definite pe spaţiul X .
L( X , K ) = { f | f : X → K , f liniare }
Vom organiza această mulţime ca un spaţiu vectorial.
1) oricare ar fi f , g ∈ L( X , K ) , ( f ⊕ g )( x ) = f ( x ) + g ( x ) , unde “+” este adunarea din corpul

K.
2) oricare ar fi λ ∈ K şi oricare ar fi f ∈ L( X , K ) , (α ⊗ f )( x ) = αf ( x )
Cu aceste proprietăţi, spaţiul vectorial reprezintă un dual algebric.
DEMONSTRAŢIE :
Oricare ar fi f , g ∈ L( X , K ) ⇒ ( f ⊕ g )( x ) ∈ L( X , K )
• f este funcţională liniară ⇒ oricare ar fi α , β ∈ K , oricare ar fi x, y ∈ X este adevărată
relaţia : f (αx + βy ) = αf ( x ) + βf ( y )
• g este funcţională liniară ⇒ oricare ar fi α , β ∈ K , oricare ar fi x, y ∈ X este adevărată
relaţia : g (αx + βy ) = αg ( x ) + βg ( y )
(f ⊕ g )[αx + βy ] = f (αx + βy ) + g (αx + βy ) = αf ( x ) + βf ( y ) + αg ( x ) + βg ( y ) =

= α [ f ( x ) + g ( x )] + β [ f ( y ) + g ( y )] = α ( f ⊕ g ) + β ( f ⊕ g )
• Asociativitate : (( f ⊕ g ) ⊕ h )( x ) = ( f ⊕ (g ⊕ h ))( x ) , oricare ar fi f , g ∈ L( X , K ) .

• Element neutru : există ν ∈ L( X , K ) , ν ( x ) = 0 , oricare ar fi x ∈ X .
• Element simetric : oricare ar fi f ∈ L( X , K ) , există (− f ) ∈ L( X , K ) , astfel
încât
(− f )(x ) = − f (x ) .
• Comutativitate : ( f ⊕ g )( x ) = (g ⊕ f )( x ) , oricare ar fi f , g ∈ L( X , K ) .
• (1 ⊗ f )( x ) = f ( x ) , oricare ar fi f ∈ L( X , K ) .
• (α ⊗ β ) ⊗ f (x ) = α ⊗ (β ⊗ f (x )) , oricare ar fi f , g ∈ L( X , K ) , oricare ar fi α , β ∈ K .

• α ⊗ ( f ( x ) ⊕ g ( x )) = (α ⊗ f ( x ) ⊕ αg ( x )) , oricare ar fi f , g ∈ L( X , K ) , oricare ar fi α ∈ K .
Dualul algebric se mai numeşte spaţiul adjunct sau conjugat al lui X.
2.5. Funcţionale biliniare
Fie (X,K) şi fie (Y,K) două spaţii vectoriale definite peste acelaşi corp de scalari K.
DEFINIŢIA 2.5.1.
O aplicaţie f : X × Y → K se numeşte funcţională biliniară dacă :

1) f ( α1 x’ + α2 x’’ , y ) = α1 f ( x’ , y ) + α2 f ( x’’ , y ) , oricare ar fi α1 , α2 ∈ K, oricare ar fi x’ ,
x’’ ∈ X şi oricare ar fi y ∈ Y ( funcţionala f este liniară în raport cu prima variabilă, x’ ) .
2) f ( x , β1 y’ + β2 y’’ ) = β1 f ( x , y’ ) + β2 f ( x , y’’ ) , oricare ar fi β1 , β2 ∈ K, oricare ar fi y’ ,
y’’ ∈ Y şi oricare ar fi x ∈ X ( funcţionala f este liniară în raport cu a doua variabilă, y’ ) .
2.6. Matricea unei funcţionale biliniare
Fie (X,K) un spaţiu vectorial, dimX = m ; fie E = { e1 , e2 ,…, em } o bază în X.

Fie (Y,K) un spaţiu vectorial, dimY = n ; fie Y = { g1 , g2 ,…, gn } o bază în Y.
m n
x = ∑ α i ei y = ∑β jg j
Oricare ar fi x ∈ X , i =1 şi oricare ar fi y ∈ Y , i =1 .
Fie f : X × Y → K , o funcţională biliniară,
⎛ m ⎞ m n
f ( x, y ) = f ⎜⎜ ∑ α i ei , ∑ β j g j ⎟⎟ = ∑∑ α i β j f (ei , g j )
n
⎝ i =1 j =1 ⎠ i =1 j =1
Notăm (1) aij = f ( ei ,gj ) , i = 1 , … , m , j = 1 , … , n ⇒ obţinem matricea A ( aij ).
DEFINIŢIA 2.6.1.
Matricea A ( aij ) ∈ Mnxm (K) unde aij = f ( ei ,gj ) , i = 1 , … , m , j = 1 , … , n se

numeşte matricea funcţionalei biliniare corespunzătoare bazelor E din spaţiul X şi G din spaţiul
Y.
m n
f(x,y)=
∑∑α β
i =1 j =1
i j a ij
= α1 ( β1 a11 + β2 a12 + … + βn a1n ) +
+ α2 ( β1 a21 + β2 a22 + … + βn a2n ) + … +
+ am ( β1 am1 + β2 am2 + … + βn amn ) = XT AY .

⎛ a11 Κ a1n ⎞ ⎛ β1 ⎞
⎜ ⎟ ⎜ ⎟
A=⎜ Μ ⎟ Y = ⎜ Μ⎟
⎜a a mn ⎟⎠ ⎜β ⎟
XT = ( α1 ,α2 , … , αm ) , ⎝ m1 Κ , ⎝ n⎠
(2) f ( x , y ) = XT AEG YG
2.7. Schimbarea matricei unei funcţionale biliniare la schimbarea bazelor
Fie (X,K) un spaţiu vectorial, dimX = m ; fie E = { e1 , e2 ,…, em } o bază în X.

Fie (Y,K) un spaţiu vectorial, dimY = n ; fie Y = { g1 , g2 ,…, gn } o bază în Y.
m n
x E = ∑ α i ei yG = ∑ β j g j
Fie i =1 şi i =1 .
Fie f : X × Y → K o funcţională biliniară .
Fie A matricea funcţionalei biliniare f corespunzătoare bazei E din spaţiul X şi bazei G din
spaţiul Y .
Fie F = { f1 , f2 , … , fm } o altă bază în spaţiul X .
Fie CEF matricea de trecere de la baza E la baza F.
⎧ f f = c11 e1 + c12 e 2 + Κ + c1m e m

⎪
⎨Μ
⎪ f = c e + c e +Κ + c e
⎩ m m1 1 m2 2 mm m
Fie H = { h1 , h2 , … , hm } o altă bază în spaţiul Y .
⎧h f = d 11 g 1 + d 12 g 2 + Κ + d 1m g m
⎪
⎨Μ
⎪h = d g + d g + Κ + d g
⎩ m m1 1 m2 2 mm m
Fie B matricea funcţionalei biliniare f corespunzătoare bazei F din spaţiul X şi bazei H din
spaţiul Y.
(3) f ( x , y ) = XTE A YG
(4) f ( x , y ) = XTF B YH
(5) XF = ( CT )-1 XE
(6) YH = ( DT )-1 YG
(4) ⇒ f ( x, y ) = [(C T )−1 X E ] B (D T ) YG ⎫

T −1
⎪
⎪
(∗) ( A • B )T = B T AT ⎬⇒
⎪ [ ]
f ( x, y ) = X ET C −1 B (D T ) YG ⎫⎪
−1
(∗ ∗) (C −1 )T = (C T )−1 ⎪⎭ (3)
⎬⇒
⎪⎭
⇒ A = C –1 B ( DT )-1 | • C ⇒ C A = C C –1 B ( DT )-1 ⇒ DT | C A = B ( DT )-1 ⇒

T
⇒ B=C•A•D

CAPITOLUL 3
SPAŢII EUCLIDIENE
3.1. Produs scalar
Fie (V,R) un spaţiu vectorial .
DEFINIŢIA 3.1.1.
O aplicaţie < , > : V × V → R se numeşte produs scalar real dacă :

1) < x , y > = < y , x > , oricare ar fi x, y ∈V .
2) < λx , y > = λ < x , y > , oricare ar fi R şi oricare ar fi x, y ∈V .
3) < x + y , z > = < x , z > + < y , z > , oricare ar fi x, y , z ∈V .
4) < x , x > ≥ 0 , oricare ar fi x ∈V şi < x , x > = 0 ⇔ x = 0 .
EXEMPLUL 1 :
Fie V = C [ a , b ] = { f | f : [a, b] → R , f continue } , f , g ∈ C [ a , b ]
∫ f (x )g (x )dx
b
Prin definiţie, < f , g > = a . Să se arate că < f , g > reprezintă un produs
scalar .
f ( x )g ( x )dx = ∫ f ( x )g ( x )dx = < g , f >
b b
1) <f,g>= ∫ a a
λf ( x )g ( x )dx = λ ∫ f ( x )g ( x )dx = λ < f , g >

b b
2) <λf,g>= ∫ a a
< f + g , h > = ∫a [ f ( x ) + g ( x )]h( x )dx = ∫a f ( x )h( x )dx + ∫a g ( x )h( x )dx =

b b b
3)
=<f,h>+<g,h>
( x )dx ≥ 0
b
∫ f 2
4) < f , f > = a şi < f , f > = 0 ⇔ f ( x ) = 0 oricare ar fi x ∈ [ a , b ]
b
¾ presupunem că f ( x ) = 0 ⇒ < f , f > = ∫
a
0dx = 0
( x )dx = 0
b
∫ f 2
¾ presupunem că < f , f > = 0 ⇒ a
presupunem că f ≠ 0 pe [ a , b ] ⇒ există ξ ∈ [ a , b ] astfel încât f (ξ ) ≠ 0
Dar funcţia f este continuă ⇒ există V ε astfel încât x ∈ V ε ⇒ f ( x ) ≠ 0 ⇒

ξ −ε
f ( x )dx
( x ) ≠ 0 ⇒ ∫ξ ε
2
⇒ f2 > 0 , aceasta fiind o contradicţie cu faptul că
−
( x )dx = 0
b
∫ f 2
a ⇒ f ( x ) = 0 , oricare ar fi x ∈ [ a , b ] .
EXEMPLUL 2 :

V = Rn x ∈ Rn , x = ( x1 , x2 , … , xn )T , y = ( y1 , y2 , … , yn )T
n
prin definiţie, < x , y > =

∑x y
i =1
i i
.
EXEMPLUL 3 :
V = P2 [ R ] , f ,g ∈ P2 [ R ]
∫ f (x )g (x )dx
1
prin definiţie, < f ,g > = 0 .
PROPRIETÃŢILE PRODUSULUI SCALAR:
1) Oricare ar fi x ∈V ⇒ < θ , x > = < x ,θ > = 0

Demonstraţie : < 0 • θ , x > = 0 • < θ , x > = 0 .
2) < λ x + µ y , z > = λ < x , z > + µ < y , z >

Demonstraţie : < λ x + µ y , z > = < λ x , z > + < µ y , z > = λ < x , z > + µ < y , z > .
Consecinţă:
< λ x + µ y , λ x + µ y > = λ2 < x ,x > + λ µ < x , y > + µ λ < y , z > + µ2 < y , y > .
3.2. Spaţiu euclidian
Fie (V,R) un spaţiu vectorial finit dimensional , dim V = n .
DEFINIŢIA 3.2.2.
Un spaţiu vectorial (V,R) finit dimensional, peste care s-a definit un produs scalar se
numeşte spaţiu euclidian .
EXEMPLUL 1 : x2
V = R2 , fie X ∈ R2 , X( x1 ,x2 )
-x2 •X( x1 ,x2 )
lung || x || = x1 + x 2
2 2
(lungimea vectorului x ) |
< x , x > = x21 + x22 x1 x1
|| x || = < x, x >
EXEMPLUL 2 :
(-1,2) • 2-
Fie X( 2 , 1 ) şi Y ( -1 , 2 )
< x , y > = 2( -1 ) + 1• 2 = 0 1- φ •(2,1)
< x, y >
cos φ = || x || • || y || | | |

-1 1 2
Observaţie :
π
Dacă < x , y > = 0 ⇒ cos φ = 0 ⇒ φ = 2 deci vectorii x şi y sunt ortogonali.
DEFINIŢIA 3.2.2.
Fie (V,R) un spaţiu euclidian . Vectorii x , y ∈ V sunt ortogonali ( x⊥y ) dacă < x , y > =
0.
3.3. Inegalitatea Cauchy – Buniakowski – Schwartz în spaţii euclidiene
Oricare ar fi x , y doi vectori ce aparţin spaţiului euclidian (V,R) ,

| < x , y > | ≤ || x || • || y ||
DEMONSTRAŢIE :
Cazul 1 : < x , y > = 0 ⇒ inegalitatea este satisfăcută .
Cazul 2 : < x , y > ≠ 0 ⇒ x ≠ θ şi y ≠ θ ( conform proprietăţii 1) ) .
Considerăm λ ∈ R ( oarecare ) .
< x − λy, x − λy >

1 4 44 2 4 4 43
≥0 = < x , x > - λ < y , x > - λ < x , y > + λ2 < y , y > =
< 2 x3>
1 x, < y>
14 y,
2 43
= ⇓ - 2 λ < x , y > + λ2 ⇓ ≥0 ⇔
|| x ||2 || y ||2
⇔ λ2 || y ||2 – 2 λ < x , y > + || x ||2 ≥ 0 , oricare ar fi λ ∈ R .
⎧|| y ||2 > 0

⎨ ⇔
⎩∆ ≤ 0 < x , y >2 - || y ||2 • || x ||2 ≤ 0 ⇔ < x , y >2 ≤ || x ||2 • || y ||2 ⇔
⇔ |< x , y >| = || x || • || y || .
3. 4 . Produs scalar complex
Fie (V,C) un spaţiu vectorial finit dimensional peste C .
DEFINIŢIA 3.4.1.
O aplicaţie < , > : V × V → C se numeşte produs scalar complex dacă :

1) < x , y > = < x, y > , oricare ar fi x, y ∈V .
2) < λ x , y > = λ < x , y > , oricare ar fi C şi oricare ar fi x, y ∈V .
3) < x + y , z > = < x , z > + < y , z > , oricare ar fi x, y , z ∈V .
4) < x , x > ≥ 0 şi < x , x > = 0 ⇔ x = θ , oricare ar fi x ∈V .

COROLAR :
<x,λy>= λ<x,y>
DEMONSTRAŢIE :
< x , λ y > = < λy , x > = λ < y , x > = λ < x , y > .
EXEMPLUL 1 :
Fie V = C .
x ∈ C n ⇒ x = ( x1 , x 2 , Κ , x n ) , x i ∈ C ,
T
i=1,…,n .
y ∈ C n ⇒ y = ( y1 , y 2 , Κ , y n ) , y i ∈ C , j = 1 , … , n .
T
prin definiţie , < x , y > =

∑x
i =1
i yi
.
DEFINIŢIA 3.4.2.
Fie (V,K) un spaţiu euclidian de dimensiune finită , unde K este R sau C . Vectorii x , y ∈
V sunt ortogonali dacă < x , y > = 0 .
3.5. Elemente ortogonale într-un spaţiu euclidian
Fie (V,K) un spaţiu euclidian , unde K este R sau C .

Fie A ⊂ V , fie x 0 ∈V .
DEFINIŢIA 3.5.1.
Vectorul x0 este ortogonal pe mulţimea A dacă x0 este ortogonal pe toţi vectorii mulţimii A,
adică :
< x0 , a > = 0 , oricare ar fi a ∈ A . ( notăm x 0 ⊥A )
DEFINIŢIA 3.5.2.
Mulţimea tuturor elementelor ortogonale pe mulţimea A se numeşte complementul

ortogonal al mulţimii A şi-l notăm astfel :
(1) A ⊥ = {x ∈V | x⊥A} .
PROPOZIŢIA 3.5.1.
Complementul ortogonal al mulţimii A este un subspaţiu al spaţiului V .
DEMONSTRAŢIE :
Din (1) ştim că mulţimea A ⊥ este inclusă în spaţiul V .

x ∈ A ⊥ ⇒< x, a >= 0 , oricare ar fi a ∈ A .
y ∈ A ⊥ ⇒< y , a >= 0 , oricare ar fi a ∈ A .

< x + y , a > = < x , a > + < y , a > = 0 , oricare ar fi a ∈ A ⇒ x + y ∈ A ⊥ .

< λ x , a > = λ < x , a > = 0 , oricare ar fi a ∈ A .
PROPOZIŢIA 3.5.2.
Fie (V,K) un spaţiu euclidian, unde K este R sau C .

Fie vectorii x1 , x2 , … , xn ∈ V ,nenuli şi ortogonali doi câte doi . Atunci vectorii x1 , x2 ,
… , xn sunt liniar independenţi .
DEMONSTRAŢIE :
Din ipoteză ştim că x i ≠ θ , i = 1 , … , n .

x i ⊥x j , oricare ar fi i , j = 1 , … , n , i ≠ j ⇒ < x , x > = 0 pentru i şi j = = 1 , … ,
i j
n, i≠ j .
n
⇔ ∑ λi x i = θ
Fie combinaţia liniară λ1 x1 + λ2 x2 + … + λn xn = θ i =1 .
n
< ∑ λi x i , x j >
⇒ λ1 < x1 , x j > + Κ + λi −1 < x j −i , x j > + λ j < x j , x j > +
11=12 3 1 44 2 4 43 1 4 4 2 4 43 1 44 2 4 43
|| =0 || ||
θ 0 0 diferit de zero
+ λ j +1 < x j +1 , x j > + Κ + λ n < x n , x j > = 0
1 4 42 4 43 1 44 2 4 43
|| || ⇒
0 0
⎧λ j < x j , x j >= 0
⎨ ⇒ λj = 0
⇒⎩< x j , x j >= 0 , oricare ar fi j = 1 , … , n .
PROPOZIŢIA 3.5.3.
Vectorii x1 , x2 , … , xn ∈ V ( unde V este un spaţiu euclidian ) , sunt liniar
< x1 , x1 > < x1 , x 2 > Κ < x1 , x n >

< x 2 , x1 > < x 2 , x 2 > Κ < x2 , xn >
det H =
Μ
dependenţi ⇔ < x n , x1 > < x n , x 2 > Κ < xn , xn > = 0 . (3)
DEMONSTRAŢIE :
Presupunem că x1 , x2 , … , xn sunt liniar dependenţi .

i) dacă există xi = θ , atunci detH = 0 .
ii) presupunem că toţi x i ≠ 0 ( i = 1 , … , n ) .
n
Dacă xi sunt liniar dependenţi, atunci

∑λ x
i =1
i i =θ
este adevărat fără ca toţi scalarii λi să fie nuli
(i=1,…,n).

n
< ∑ λi x i , x j >
11=12 3
|| = 0 , oricare ar fi j = 1 , … , n
θ
n
⇒< ∑ λi x i , x1 >
- dacă j = 1 i =1 =0
……………………………………… ⇒ obţinem un sistem liniar şi omogen de
n
n
⇒< ∑ λi x i , x n >
- dacă j = n i =1 =0 ecuaţii cu n necunoscute.
Sistemul are soluţia nebanală ( din ipoteză ) , deci detH = 0 .
3.6. Baze ortogonale ; Teorema Gramm - Schmidtt
Fie V un spaţiu euclidian real sau complex n dimensional .

Fie B = { b1 , b2 , … , bn } o bază în V.
DEFINIŢIA 3.6.1.
Baza B este ortogonală dacă bi ⊥b j , i = 1 , … , n , i ≠ j . ( deci o bază este ortogonală

când vectorii ei sunt ortogonali doi câte doi )
DEFINIŢIA 3.6.2.
O bază ortogonală B = { b1 , b2 , … , bn } este ortonormală dacă || bi || = 1 , unde i = 1 ,

…,n .
EXEMPLUL 1 :
versori ai axelor de coordonate
< e1 , e2 > = 0
e2( 0,1 )- || e1 || = || e2 || = 1
|
0 e1( 1,0 )
TEOREMA GRAMM – SCHMIDTT :
Fie V un spaţiu euclidian , dim V = n . Atunci există în V o bază ortogonală .
DEMONSTRAŢIE :
Fie F = { f1 , f2 , … , fn } o bază în spaţiul V .

Fie E = { e1 , e2 , … , en } o bază ortogonală .
e1 = f1

e2 = f2 + λ21 e1
e3 = f3 + λ32 e2
………………
ei = fi + λii-1 ei-1 + λii-2 ei-2 + … + λi1 e1
……………………………………….
en = fn + λnn-1 en-1 + λnn-2 en-2 + … + λn1 e1
Vom determina scalarii λij ( i = 2, … , n , j = 1 , … , n ) astfel încât e1 , e2 , … , en să fie

ortogonali doi câte doi .
¾ e1 ⊥e2 ⇒< e1 , e 2 >= 0

< e1 , e2 > = < f2 + λ21 e1 , e1 > = < f2 , e1 > + λ21 < e1 , e1 > = 0
< f 2 , e1 >
λ21 = −
< e1 , e1 >
¾ e3 ⊥e1 şi e3 ⊥e 2 ⇒ < e3 , e1 > = 0 şi < e3 , e2 > = 0

< e3 , e1 > = < f3 + λ32 e2 + λ31 e1 , e1 > = < f3 , e1 > + λ32 < e2 , e1 > + λ31 < e1 , e1 >= 0
< f 3 , e1 >
λ31 = −
< e1 , e1 >
< e3 , e2 > = < f3 + λ32 e2 + λ31 e1 , e2 > = < f3 , e2 > + λ32 < e2 , e2 > + λ31 < e1 , e2 >= 0
< f 3 , e2 >
λ32 = −
< e2 , e2 >
În general , ei ⊥e1 , ei ⊥e 2 , Κ , ei ⊥ei −1 .

< eI , e1 > = < fI + λii-1 eI-1 + λii-2 eI-2 + … + λi1 e1 , e1 > = < fI ,e1 > + λii-1 < eI-1 , e1 > +
+ λii-2 < eI-2 , e1 > + … + λi1 < e1 , e1 > = 0 .
< f i , ei > < f i , ei −1 >

λi 1 = − λii −1 = −
⇒ < e1 , e1 > < ei −1 , ei −1 >
< fi , e j >
λij = −
În general , < ej,ej > ( i = 2, … , n , j = 1 , … , n ) .
Am obţinut astfel n vectori e1 , e2 , … , en ortogonali doi câte doi ⇒ vectorii sunt liniar
independenţi . Ştim că dimensiunea spaţiului este n , deci vectorii e1 , e2 , … , en formează o
bază ortogonală .
EXEMPLUL 2 :
Fie ( R3 , R ) un spaţiu euclidian.

x ∈ R3 , x = ( x1 , x2 , x3 )T ; y ∈ R3 , y = ( y1 , y2 , y3 )T
3
< x, y >= ∑ x i y i
Fie produsul scalar i =1 .
⎛1 ⎞ ⎛1 ⎞ ⎛ 0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
f 1 = ⎜1 ⎟ f 2 = ⎜ 0⎟ f 3 = ⎜1 ⎟
⎜0⎟ ⎜1 ⎟ ⎜ 0⎟
Fie F = { f1 , f2 , f3 } unde ⎝ ⎠ , ⎝ ⎠ , ⎝ ⎠ . Fie E = { e1 , e2 , e3 } .
⎧e1 = f 1 ⎛1 ⎞
⎪ ⎜ ⎟
⎨e 2 = f 2 + λ21 e1 ⇒ e1 = ⎜1 ⎟
⎪e = f + λ e + λ e ⎜0⎟
⎩ 3 3 32 2 31 1 ⎝ ⎠
e1 ⊥e2 ⇒ < f + λ e , e > = 0 ⇔ < f , e > + < e , e > = 0

2 21 1 1 2 1 1 1
< f 2 , e1 > 1
λ21 = − =−
<f ,e >=1,<e ,e >=2 ⇒ < e1 , e1 > 2
2 1 1 1
⎛1 ⎞
⎜ ⎟
⎛1 ⎞ ⎛1 ⎞ ⎜ 2 ⎟
⎜ ⎟ 1 ⎜ ⎟ ⎜ − 1⎟
e 2 = ⎜ 0 ⎟ − ⎜1 ⎟ = ⎜ ⎟
⎜1 ⎟ 2 ⎜ 0 ⎟ ⎜ 2 ⎟
⎝ ⎠ ⎝ ⎠ 1
⎜ ⎟
⎜ ⎟
⎝ ⎠
e3 ⊥e1 ⇒ < f + λ e + λ e , e >= 0 ⇔ < f , e > + λ < e , e > + λ < e , e >=0
3 32 2 31 1 1 3 1 32 2 1 31 1 1
< f 3 , e1 > 1
λ31 = − =−
<f ,e >=1 ⇒ < e1 , e1 > 2
3 1
e3 ⊥e 2 ⇒ < f + λ e + λ e , e >= 0 ⇔ < f , e > + λ < e , e > + λ < e , e >=0

3 32 2 31 1 1 3 1 32 2 1 31 1 2
< f ,e > 1
−
1 3 λ32 = − 3 2 =
<f ,e >= 2 , <e ,e >= 2 ⇒ < e2 , e2 > 3
3 2 2 2
⎛ 1 ⎞ ⎛ 1⎞
⎜ ⎟ ⎜− ⎟
⎛0⎞ ⎜ 2 ⎟ ⎛1 ⎞ ⎜ 3 ⎟
⎜ ⎟ 1⎜ 1⎟ 1 ⎜ ⎟ ⎜1 ⎟
e 3 = ⎜1 ⎟ + − − ⎜1 ⎟ = ⎜
⎜0⎟ 3 ⎜ 2 ⎟ 2⎜ ⎟ 3 ⎟
⎝ ⎠ ⎜ 1 ⎟ ⎝ 0⎠ ⎜ ⎟
⎜ ⎟ ⎜ 1 ⎟
⎝ ⎠ ⎜ ⎟
⎝3 ⎠
PROPOZIŢIA 3.6.1.
Fie (V,K) un spaţiu euclidian, dim V = n şi fie V0 ⊂ V un subspaţiu al lui V . Fie B0 =

{ b1 , b2 , … , bn } . Vectorul a ∈ V este ortogonal pe V0 dacă şi numai dacă a este ortogonal pe B0 .

DEMONSTRAŢIE :
1) Presupunem că a ∈ V este ortogonal pe V0 ⇒ < a , x > = 0 , oricare ar fi x ∈ V0 .

Din ipoteză ştim că bi ∈ V0 ⇒ < a , bi > = 0 ( i = 1 , … , p ) ⇒ a ⊥ B0 .
2) Presupunem că a ⊥ B0 ⇒ < a , bi > = 0 ( i = 1 , … , p ) .

Fie x ∈ V0 ⇒ x = λ1 b1 + λ2 b2 + … + λp bp .
< a , x > = < a , λ1 b1 + λ2 b2 + … + λp bp > = λ1 < a , b1 > + λ 2 < a , b2 > + … +
+ λ p < a, b p >= 0 ⇒ a⊥V0 .
3.7. Izomorfismul spaţiilor euclidiene
Fie V şi W două spaţii euclidiene peste corpul K, unde K este C sau R .
DEFINIŢIA 3.7.1.
Spaţiul V este izomorf cu spaţiul W (V ≅ W ) dacă există ϕ : V → W bijectivă astfel încât :

1) φ ( x + y ) = φ ( x ) + φ ( y ) , oricare ar fi x , y ∈ V .
2) φ ( λ x ) = λ φ ( x ) , oricare ar fi x ∈ V şi oricare ar fi λ ∈ K .
3) < x , y > = < φ ( x ) , φ ( y ) > , oricare ar fi x , y ∈ V .
TEOREMA 3.7.1.
Fie V şi W două spaţii euclidiene peste acelaşi corp K , dim V = dim W = n .

Atunci (V ≅ W ) . ( adică două spaţii euclidiene de aceeaşi dimensiune sunt izomorfe ).
DEMONSTRAŢIE :
Fie (V,R) un spaţiu euclidian, dimV = n; fie B = { b1 , b2 , … , bn } o bază în V .

Vom demonstra că V ≅ Rn .
Dacă B este o bază în spaţiul V, conform teoremei Gramm – Schmidtt , din B vom putea
construi o bază ortonormală .
E={ e , e , … , e } , ei ⊥e j ( i = 1 , … , n , i ≠ j ), || e ||= 1, || e || = < ei , ei >
1 2 n i i
n
x = ∑ x i ei
Fie x ∈ V ⇒ i =1 ( xi ∈ R , i = 1 , … , n )
n
y = ∑ y je j
Fie y ∈ V ⇒ i =1 ( yj ∈R , j = 1 , … , n )
Definim ϕ : V → R , φ ( x ) = ( x1 , x2 , … , xn )T . Funcţia φ este un izomorfism , adică
n
φ este bijectivă şi :
1) φ ( x + y ) = φ ( x ) + φ ( y ) , oricare ar fi x , y ∈ V .
2) φ ( λ x ) = λ φ ( x ) , oricare ar fi x ∈ V şi oricare ar fi λ ∈ K .
3) < x , y > = < φ ( x ) , φ ( y ) > , oricare ar fi x , y ∈ V .
Primele două relaţii sunt evidente. O vom demonstra pe cea de – a treia.

n n n n n n
< x, y >=< ∑ x i ei , ∑ y j e j >= ∑∑ x i y j < ei , e j >= ∑ x i y i < ei , ei >= ∑ x i y i =< ϕ ( x ), ϕ ( y ) >
i =1 j =1 i =1 j =1 i =1 i =1
Rezultă astfel că V ≅ Rn
W ≅ Rn , ψ : W → R n ⇒ ψ bijectivă , deci există ψ −1 : R n → W , bijectivă .
ϕ :V → R n ⎫
⎬ ⇒ ψ οϕ : V → W
−1
ψ −1
: R →W ⎭
n
este o funcţie care realizează un izomorfism între spaţiile V şi
W.
OBSERVAŢIE : Demonstraţia în cazul în care corpul de scalari este C este asemănătoare.
3.8. Proiecţia unui vector pe un subspaţiu
Fie V un spaţiu vectorial euclidian şi fie V1 ⊂ V ( V1 un subspaţiu liniar al lui V ).

Fie f ∈ V şi fie f0 ∈ V1 astfel încât ( f – f0 ) este perpendicular pe V1 .
DEFINIŢIA 3.8.1.
Vectorul f0 cu aceste proprietăţi se numeşte proiecţia vectorului f pe subspaţiul V1 . ( f0

= prV 1 f )
PROPOZIŢIA 3.8.1.
Dacă există f0 ∈ V1 , f0 = prV 1 f , atunci : || f – f0 || ≤ || f – f 1 || oricare ar fi

f1 ∈ V .
DEMONSTRAŢIE :
|| f – f1 || 2 = < f – f1 , f – f1 > = < f – f 0 + f – f0 , f – f0 + f0 – f1 > = < f – f0 , f – f0 > +

+ 2< f – f0 , f1 – f0 > + < f0 – f1 , f0 – f1 > = || f – f0 ||2 + 2< f – f0 , f1 – f0 > + || f0 – f1 || 2=
= || f – f0 ||2 +|| f0 – f1 || 2 ⇒ || f – f1 || 2 = || f – f0 ||2 +|| f0 – f1 || 2
⇒ || f – f1 || 2 ≥ || f – f0 ||2 ⇒ || f – f1 || ≥ || f – f0 ||
Imaginea geometrică :
f-f1

f1 f-f0
f0
f0-f1
3.9. Calculul proiecţiei unui vector pe un subspaţiu
Fie V un spaţiu euclidian . Fie V1 ⊂ V un subspaţiu al lui V şi fie f un vector

oarecare din V.
Presupunem dim V = p ⇒ există E = { e1 , e2 , … , ep } o bază ortonormală.
Prin definiţia vectorului f0 ştim că ( f − f 0 )⊥V1 , adică < f – f0 , x > = 0 , oricare ar fi
vectorul x din V1 . ( * )
Din ( * ) şi din faptul că un vector este ortogonal pe un subspaţiu dacă este ortogonal pe
vectorii bazei , rezultă că < f – f 0 , ei > = 0 , oricare ar fi i = 1, … , p .
< f , ei > - < f0 , ei > = 0 ⇔ < f0 , ei > = < f , ei > , oricare ar fi i = 1, … , p .

p p
f0 = ∑c je j ⇒< ∑ c j e j , ei >=< f , ei >
f 0 ∈V1 ⇒ j =1 (**) i =1 , oricare ar fi i = 1, … , p ⇔
p
∑c j < e j , ei >=< f , ei >⇒

⇔ j =1
⎧c1 < e1 , e1 > + c 2 < e 2 , e1 > + Κ + c p < e p , e1 >=< f , e1 >

⎪
⎪c1 < e1 , e 2 > + c 2 < e 2 , e 2 > + Κ + c p < e p , e 2 >=< f , e 2 >
⇒⎨
⎪Μ
⎪c1 < e1 , e p > + c 2 < e 2 , e 2 > + Κ + c p < e p , e p >=< f , e 2 >
⎩
< e1 , e 2 > < e 2 , e1 > Κ < e p , e1 >

< e1 , e 2 > < e 2 , e 2 > Κ < e p , e1 >
H= ≠0
Μ
< e1 , e p > < e 2 , e p > Κ < ep ,ep >
pentru că vectorii e1 , e2 , … , ep sunt liniar independenţi .
Deci sistemul are soluţie unică c1 , c2 , … , cp pe care o înlocuim în relaţia (**) .
EXEMPLUL 1 :
Fie V = R3 , f ∈ R3 , f = ( 1 , 2 , 1 )T .
Fie V1 ⊂ V un subspaţiu al lui V , V1 = {x ∈V | x = ( x1 , x 2 ,0 ) } .
T
O bază în V1 este { e1 , e2 } unde : e1 = ( 1 , 0 , 1 ) şi e2 = ( 0 , 1 , 0 ) .

Trebuie să calculăm f0 ∈ V1 astfel încât ( f − f 0 )⊥V1 .

f0 = c1 e1 + c2 e2 , ( f − f 0 )⊥V1 ⇒ (f − f 0 )⊥e1 şi (f − f 0 )⊥e 2 .
⎧< c1 e1 + c 2 e 2 , e1 >=< f , e1 > ⎧c1 < e1 , e1 > + c 2 < e 2 , e1 >=< f , e1 >

⎨ ⇒ ⎨
⎩< c1 e1 + c 2 e 2 , e 2 >=< f , e 2 > ⎩c1 < e1 , e 2 > + c 2 < e 2 , e 2 >=< f , e 2 >
< e1 ,e1 > = 1 ; < e2 , e2 > = 1 ; < f , e1 > = 1 ; < f , e2 > = 2

1- f
⇒ c1 = 1 ; c2 = 2 . ⇒ f0 = ( 1 , 2 , 0 ) . |
|
2
1 f0

CAPITOLUL 4
OPERATORI LINIARI
4.1. Noţiunea de operator liniar
Fie X şi Y două spaţii vectoriale peste acelaşi corp de scalari K .
DEFINIŢIA 4.1.1.
O aplicaţie U : X → Y se numşte operator .
DEFINIŢIA 4.1.2.
Operatorul U : X → Y este aditiv dacă U ( x + y ) = U ( x ) + U ( y ) , oricare ar fi

x, y ∈ X .
DEFINIŢIA 4.1.3.
Operatorul U : X → Y este omogen dacă U ( λ x ) = λ U ( x ) , oricare ar fi λ ∈ K şi

oricare ar fi x ∈ X .
DEFINIŢIA 4.1.4.
Operatorul U : X → Y este liniar dacă este aditiv şi omogen .
DEFINIŢIA 4.1.5. ( definiţie echivalentă )
Operatorul U : X → Y este liniar dacă , oricare ar fi λ1 , λ2 ∈ K şi oricare ar fi vectorii

x1 , x 2 ∈ X ⇒ U ( λ x + λ x ) = λ U ( x ) + λ U ( x ) .
1 1 2 2 1 1 2 2
OBSERVAŢIE : Dacă U : X → Y este liniar , atunci :
⎛ n ⎞ n
U ⎜ ∑ λi x i ⎟ = ∑ λ i U ( x i )
⎝ i =1 ⎠ i =1 oricare ar fi λ1 , λ2 ∈ K şi oricare ar fi x1 , x 2 ∈ X .
PROPRIETATEA 4.1.1.
Dacă U : X → Y este aditiv , atunci U ( θ x ) = θ y .
DEMONSTRAŢIE :
x + θ = x , oricare ar fi x ∈ X .
U (x + θ ) = U ( x ) .

Din proprietatea de aditivitate, rezultă că U ( x ) + U ( θx ) = U ( x ) ⇒ U ( θx ) = θy .
PROPRIETATEA 4.1.2.
Dacă U : X → Y este aditiv , atunci U ( x ) = - U ( - x ), oricare ar fi x ∈ X .
DEMONSTRAŢIE :
x+(-x)=θx ⇒ U(x+(-x))=U(θx) ⇔ U(x)+U(-x)=θy ⇒

⇒ U(x)=-U(-x).
DEFINIŢIA 4.1.6.
Fie U : X → Y un operator liniar . Imaginea operatorului este:
Im U = { y ∈ Y | există x ∈ X astfel încât U ( x ) = y } .
PROPOZIŢIA 4.1.1.
Dacă operatorul U : X → Y este liniar , atunci Im U este un subspaţiu liniar al lui Y .
DEMONSTRAŢIE :
1) Fie y1 ∈ Im U ⇒ există x1 ∈ X astfel încât U ( x1 ) = y1 .

Fie y2 ∈ Im U ⇒ există x 2 ∈ X astfel încât U ( x2 ) = y2 .
U ( x1 + x2 ) = U ( x1 ) + U ( x2 ) = y1 + y2 ∈ Y ⇒ y1 + y2 ∈ Im U .
2) Fie y ∈ Im U ⇒ există x ∈ X astfel încât U ( x ) = y .

U ( λ x ) = λ U ( x ) = λ y ∈ Y ⇒ λ y ∈ Im U .
Deci imaginea lui U este un subspaţiu liniar .
COMPUNEREA OPERATORILOR LINIARI
Fie X , Y , Z trei spaţii vectoriale, definite peste acelaşi corp de scalari K .

Fie operatorii liniari :
U : X →Y ⎫
⎬
V : Y → Z ⎭ , W = V οU , W : X → Z , W ( x ) = V ( U ( x ) ) .
PROPOZIŢIA 4.1.1.
Dacă U şi V sunt liniari, atunci W este liniar .
DEMONSTRAŢIE :
Fie λ1 , λ2 ∈ K , fie x1 , x 2 ∈ X .
W( λ1 x1 + λ2 x2 ) = V( U( λ1 x1 + λ2 x2 ) ) = V( λ1 U( x1 ) + λ2 U( x2 ) )= λ1 V( U( x1 ) ) + + λ2 V( U

( x2 ) ) = λ1 W( x1 ) + λ2 W( x2 ) .
INVERSAREA OPERATORILOR LINIARI
Fie X şi Y două spaţii vectoriale peste acelaşi corp de scalari K şi fie U : X → Y un operator
liniar .
DEFINIŢIA 4.1.7.
Operatorul U este inversabil dacă stabileşte o corespondenţă bijectivă de la spaţiul X la

spaţiul Y .
−1
Atunci există U −1 : Y → X , definit astfel : U ( y ) = x ⇔ U ( x ) = y .
U-1
x• U • U(x)=y
X Y
PROPOZIŢIA 4.1.2.
Dacă U : X → Y este un operator liniar inversabil, atunci operatorul U −1 : Y → X este

liniar .
4.2. Nucleul unui operator liniar
Fie X şi Y două spaţii vectoriale peste acelaşi corp K şi fie U : X → Y un operator .
PROPOZIŢIA 4.2.1.
Se numeşte nucleul operatorului U, mulţimea : KerU = {x ∈ X | U ( x ) = θy} .
DEMONSTRAŢIE :
1) Fie x1 ∈ Ker U ⇒ U( x1 ) = θ y .
Fie x2 ∈ Ker U ⇒ U( x2 ) = θ y .
U( x1 + x2 ) = U( x1 ) + U( x2 ) = θ y + θ y = θ y ⇒ x1 + x 2 ∈ Ker U .
2) Oricare ar fi λ ∈ K , oricare ar fi x ∈ Ker U, rezultă că:
U( λ x ) = λ U ( x ) = λ θ y = θ y ⇒ λ x ∈ Ker U .
Deci Ker U este un subspaţiu al spaţiului Ker U .
TEOREMA 4.2.1.

Fie U : X → Y un operator liniar . Operatorul U este inversabil dacă şi numai dacă Ker U
={θx}.
DEMONSTRAŢIE :
1) Presupunem că U : X → Y este un operator inversabil ⇒ U este bijectiv ⇒ ⇒ Im U =

Y ( adică U este surjectiv ).
Oricare ar fi x1 , x2 ∈ X , x1 ≠ x2 ⇒ U( x1 ) ≠ U( x2 ) ( adică U este injectiv ) .
Din faptul că U este liniar rezultă că U( x ) = θ y .
Deoarece operatorul U este bijectiv , U este singurul vector cu proprietăţile de mai sus
⇒ Ker U = { θ x } .
3) Presupunem că Ker U = { θ x } .
Im U = Y ⇒ U este surjectiv.
Fie x , y ∈ X , x ≠ y . Presupunem că :
U( x ) = U( y ) ⇒ U( x ) – U( y ) = θ y ⇒ U( x ) + U ( - y ) =θ y ⇒ U( x + ( - y ) ) = θ y ⇔ U( x –
y ) = θ y ⇒ x – y ∈ Ker U.
Dar Ker U = { θ x } ⇒ x – y = θ x ⇒ x = y ceea ce reprezintă o contradicţie cu ipoteza ca x ≠ y

⇒ U este injectiv .
Deci U este bijectiv ⇒ este inversabil .
4.3. Matricea unui operator liniar
Fie (X,K) un spaţiu vectorial , dim X = m , E = { e1 , e2 , … , em } o bază în

m
∑ α i ei .
spaţiul X , oricare ar fi x ∈ X ⇒ xE = i =1
Fie (Y,K) un spaţiu vectorial , dim Y = n , G = { g1 , g2 , … , gm } o bază în
n
∑β jg j .
spaţiul Y , oricare ar fi y ∈ Y ⇒ yE = j =1
Fie U : X → Y un operator liniar , astfel încât oricare ar fi x ∈ X ⇒ U( x ) = y
⎛ m ⎞ n
U ⎜ ∑ α i ei ⎟ = ∑ β j g j
⇒ ⎝ i =1 ⎠ j =1 .
e1 ∈ X ⇒ U( e1 ) = a11 g1 + a12 g2 + … + a1n gn

………………………………………………….. ⇒ (1) A ( aij ) , i = 1 , … , m ,
em ∈ X ⇒ U( em ) = am1 g1 + am2 g2 + … + amn gn j=1,…,n
Matricea A se numeşte matricea operatorului liniar U corespunzătoare bazei E din spaţiul X şi

bazei G din spaţiul Y .

⎛ ⎞
n ⎜ n ⎟
⎛ m ⎞ m m n m n
U ⎜ ∑ α i ei ⎟ = ∑ α iU (ei ) = ∑ α i ∑ a ij g j = ∑ ∑ α i a ij g j = ∑ ⎜ ∑ α i a ij ⎟g j
⎝ i =1 ⎠ i =1 j =1 ⎜ i =1 ⎟
⎜ 14 2β 43 ⎟
i =1 j =1 i =1 j =1
⎝ j ⎠ j = 1, n .
j =1 ⇒ β1 = α1 a11 + α2 a21 + … + αm am1

⇒ Y G = A X E (2)
T
……………………………………………
j = n ⇒ βn = α1 a1n + α2 a2n + … + αm amn
SCHIMBAREA MATRICEI UNUI OPERATOR LINIAR LA SCHIMBAREA BAZEI
Fie (X,K) un spaţiu vectorial , dim X = m , E = { e1 , e2 , … , em } o bază în

m
∑ α i ei .
spaţiul X , oricare ar fi x ∈ X ⇒ xE = i =1
Fie (Y,K) un spaţiu vectorial , dim Y = n , G = { g1 , g2 , … , gm } o bază în
n
∑β jg j .
spaţiul Y , oricare ar fi y ∈ Y ⇒ yE = j =1
Fie A matricea operatorului U corespunzătoare bazelor E din spaţiul X şi G din spaţiul
Y ⇒ YG = A X E .
T
Fie F = { f1 , f2 , … , fm } o nouă bază în spaţiul X . Fie H = { g1 , g2 , … , gn } o nouă bază

în spaţiul Y .
Fie B matricea operatorului U corespunzătoare bazelor F din X şi H din Y ⇒
YH = B T X F .
Fie C matricea de trecere de la baza E la baza F, în spaţiul X.
f 1 = c11 e1 + c12 e 2 + Κ + c1n e n ⎫

⎪
Μ ⎬ ⇒ C (c ij )
f m = c m1 e1 + c m 2 e 2 + Κ + c mn e n ⎪⎭ (3) X F = (C ) X E
T −1
Fie D matricea de trecere de la baza G la baza H , în spaţiul Y.
h1 = d 11 g 1 + d 12 g 2 + Κ + d 1n hn ⎫
⎪
Μ ⎬ ⇒ D (d ij )
hm = d m1 g 1 + d m 2 g 2 + Κ + d mn g n ⎪⎭ (4) Y H = (D ) YG
T −1
Y H = B T X F ⇔ (D T ) YG = B T (C T ) X E | D T ⇒ YG = 1D T44B T2(C4 T43) X E ⇒

−1 −1 −1
AT
⇒ AT = D T B T (C T ) ⇒ A = C −1 BD | C ⇒ D −1 | CA = BD ⇒ B = CAD −1 .
−1
OBSERVAŢII :

1) dacă X = Y ⇒ E = G şi F = H ⇒ C = D ⇒ B = CAC-1 .
2) dacă în X trecem de la baza E la baza F , iar în Y avem G = H ⇒ D = In
⇒ B = CA .
3) dacă în Y trecem de la baza G la baza H , iar în X avem G = H ⇒ C = Im
⇒ B = AD-1 .
4.4. Operaţii cu operatori liniari
Fie U : X → Y un operator liniar şi fie V : X → Y alt operator liniar.
DEFINIŢIA 4.4.1.
U = V dacă , oricare ar fi x ∈ X , U( x ) = V( x ) .
DEFINIŢIA 4.4.2.
W = U + V dacă , oricare ar fi x ∈ X , W( x ) = U( x ) + V( x ) (1) .
PROPOZIŢIA 4.4.1.
Dacă U şi V sunt doi operatori liniari, atunci şi W = U + V este liniar.
DEMONSTRAŢIE :
W( α1 x1 + α2 x2 )= U( α1 x1 + α2 x2 ) + V( α1 x1 + α2 x2 ) = α1 U( x1 ) + α2 U( x2 ) +
+ α1 V( x1 ) + α2 V( x2 ) = α1 ( U( x1 ) + V( x1 ) ) + α2 ( U( x2 ) + V( x2 ) ) = α1 W( x1 ) +
+ α2 W( x2 ) , oricare ar fi α1 , α2 ∈ K şi oricare ar fi x1 , x2 ∈ X .
DEFINIŢIA 4.4.3.
Operatorul nul θ : X → Y se defineşte prin θ( x ) = θy ( θy este elementul neutru din

spaţiul vectorial Y ) .
DEFINIŢIA 4.4.4.
Operatorul opus operatorului U : X → Y este operatorul

(− U ) : X → Y , ( -U )( x ) = -U( x ) .
DEFINIŢIA 4.4.5.
Oricare ar fi λ ∈ K , λU : X → Y , ( λ U )( x ) = λ U ( x ) . (2)
PROPOZIŢIA 4.4.2.
Fie U = { U : X → Y | U liniar }. Atunci ( U , + , • ) este un spaţiu vectorial

numit spaţiul vectorial al operatorilor liniari definiţi pe spaţiul X cu valori în spaţiul Y.
OBSERVAŢIE :

Operaţiile “ + ” şi “ • ” sunt definite de relaţiile (1) şi (2) .
4.5. Vectori proprii şi valori proprii ale unui operator liniar
Fie (X,C) un spaţiu vectorial ; fie U : X → X un operator liniar .
DEFINIŢIA 4.5.1.
Un vector x ∈ X , x ≠ θ , se numeşte vector propriu al operatorului U dacă este soluţie a

ecuaţiei U( x ) = λ x , λ ∈ C (1) .
Un vector propriu se mai numeşte şi vector caracteristic .
DEFINIŢIA 4.5.2.
Scalarii λ pentru care ecuaţia (1) are soluţii nenule se numesc valorile proprii
( caracteristice ) ale operatorului U .
EXISTENŢA VALORILOR PROPRII ŞI CALCULUL LOR
Fie (X,C) un spaţiu vectorial , dim X = n ; fie U : X → X un operator liniar.

Fie A matricea operatorului U corespunzătoare unei baze oarecare :
E = { e1 , e2 , … , en } . Atunci YE = AT xE (2) .
Relaţia (1) devine (1’) AT x = λ x ⇒ (3) ( AT – λ I ) x = θ , I fiind matricea unitate de
ordinul n .
⎡⎛ a11 Κ a n1 ⎞ ⎛ λ Κ 0 ⎞ ⎤ ⎛ x1 ⎞ ⎛ 0 ⎞
⎢⎜ ⎟ ⎜ ⎟⎥⎜ ⎟ ⎜ ⎟
⎢⎜ Μ Μ⎟ − ⎜ Ο ⎟⎥⎜ Μ⎟ = ⎜ Μ⎟
⎢⎣⎜⎝ a1n Κ ⎟ ⎜
a nn ⎠ ⎝ 0 Κ λ ⎟⎠⎥⎦⎜⎝ x n ⎟⎠ ⎜⎝ 0 ⎟⎠
Relaţia (3) repezintă un sistem liniar şi omogen care are forma :
⎧(a11 − λ )x1 + a 21 x 2 + Κ + a n1 x n = 0
⎪a x + (a − λ )x + Κ + a x = 0
⎪ 12 1 22 2 n2 n
⎨
⎪ Κ Κ Κ Κ Κ Κ Κ Κ Κ Κ Κ Κ Κ
⎪⎩a1n x1 + a 2 n x 2 + Κ + (a nn − λ )x n = 0
Sistemul (3) are şi soluţii nebanale dacă determinantul sistemului este nul :
det ( AT – λI ) = 0 (4)
Ecuaţia (4) este o ecuaţie de gredul n în λ şi se numeşte ecuaţie caracteristică

Soluţiile ecuaţiei caracteristice sunt valorile proprii .
OBSERVAŢIE :

Existenţa valorilor proprii nu poate fi considerată aprioric.
EXEMPLUL 1 :
Fie U : R 3 → R 3 , x ∈ R3 , x = ( x1 , x2 , x3 )T .
U( x ) = U( x1 , x2 , x3 ) = ( x1 + x2 – x3 , x3 , -2 x2 –3 x3 ) , U( x ) = y .
⎛ 1 1 − 1⎞ ⎛λ 0 0 ⎞
⎜ ⎟ ⎜ ⎟
A = ⎜0 0 1 ⎟ λI = ⎜ 0 λ 0 ⎟
⎜ 0 − 2 − 3⎟ ⎜0 0 λ⎟
⎝ ⎠ ⎝ ⎠
1− λ 1 −1
A − λI = 0 −λ 1
0 − 2 − 3 − λ = ( 1 – λ ) ( λ2 + 3λ + 2 ) = 0 .
λ1 = 1 ; λ2 = -1 ; λ3 = -2 .
Calculul vectorilor proprii corespunzători :
¾ Pentru λ1 = 1 ⇒ U( x ) = 1*x ⇒ AT x = x .
⎛ 1 1 − 1 ⎞⎛ x 1 ⎞ ⎛ x 1 ⎞ ⎧ x1 + x 2 − x 3 = x1 ⎧x2 − x3 = 0
⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎪ ⎪
⎜0 0 1 ⎟⎜ x 2 ⎟ = ⎜ x 2 ⎟ ⇒ ⎨x3 = x2 ⇔ ⎨− x 2 + x 3 = 0
⎜ 0 − 2 − 3 ⎟⎜ x ⎟ ⎜ x ⎟ ⎪− 2 x − 3x = x ⎪− 2 x − 3x = 0
⎝ ⎠⎝ 3 ⎠ ⎝ 3 ⎠ ⎩ 2 3 3 ⎩ 2 3
Necunoscutele x2 şi x3 sunt necunoscute principale . Prima ecuaţie este ecuaţie

secundară . Determinantul sistemului este nul . ⇒ x2 = x3 = 0 .
⇒ x = ( a , 0 , 0 ) , a ∈ R \ {0} ( pentru că x este un vector nenul ) .
¾ Pentru λ2 = -1 ⇒ x = ( b , -b , b ) , b ∈ R \ {0} .
⎛c c ⎞
⎜ , ,c⎟
¾ Pentru λ3 = -2 ⇒ x = ⎝ 2 2 ⎠ , c ∈ R \ {0} .
PROPOZIŢIA 4.5.1.
Fie U : X → X , un operator liniar şi fie λ0 o valoare proprie a sa . Atunci mulţimea

(3) X λ0 = {x ∈ X | U ( x ) = λ0 x} este un subspaţiu al spaţiului vectorial X, denumit subspaţiu
propriu al spaţiului vectorial X, corespunzător valorii proprii λ0 .
OBSERVAŢIE :
Mulţimea X λ0 conţine toţi vectorii proprii corespunzători valorii proprii λ0 şi vectorul

nul.

DEMONSTRAŢIE :
1) Fie x1 , x2 ∈ X λ0 .
⇒ U( x1 ) = λ0 x1
U( x2 ) = λ0 x2
U( x1 ) + U( x2 ) = λ0 ( x1 + x2 ) ⇒ U( x1 + x2 ) = λ ( x1 + x2 ) ⇒ x1 + x2 ∈ X λ0 .
2) Oricare ar fi α ∈ C şi oricare ar fi x ∈ X λ0 ⇒ U( x ) = λ0 x .
U( α x ) = α U( x ) = α λ x = λ ( α x ) ⇒ α x ∈ X λ0 .
0 0
PROPOZIŢIA 4.5.2.
Fie U : X → X un operator liniar .

Fie λ1 , λ2 , … , λn , n valori proprii ale lui U diferite două câte două.
Fie x1 , x2 , … , xn , n vectori proprii corespunzători valorilor proprii λ1 ,
λ2 , … , λn . Atunci vectorii x1 , x2 , … , xn sunt liniar independenţi .
DEMONSTRAŢIE :
Se va demonstra propoziţia prin inducţie după n .
1) Verificare:
n =2 , λ1 ≠ λ2 , U( x1 ) = λ1 x1
U( x2 ) = λ2 x2
Fie combinaţia liniară (4) µ1 x1 + µ2 x2 = θ ( µ1 , µ2 ∈ C ) .
µ1 λ1 x1 + µ2 λ2 x2 = θ .
Înmulţim relaţia (4) cu ( -λ1 ) şi adunăm cele două relaţii . Vom obţine :
µ2 ( λ2 – λ1 ) x1 = θ ⇒ x2 ≠ θ . Dar λ1 ≠ λ2 ⇒ µ2 = 0 .
Înmulţim relaţia (4) cu ( -λ2 ) şi adunăm cele două relaţii . Vom obţine :
µ1 ( λ2 – λ1 ) x2 = θ ⇒ x1 ≠ θ . Dar λ1 ≠ λ2 ⇒ µ1 = 0 .
2) Presupunem că vectorii x1 , x2 , … , xn-1 sunt liniar independenţi şi demonstrăm că vectorii

x1 , x2 , … , xn-1 , xn sunt liniar independenţi .
µ1 x1 + µ2 x2 + … + µn-1 xn-1 = θ ⇔ µi = 0 ( i = 1 , … , n-1 ) . (5)

µ1 x1 + µ2 x2 + … + µn-1 xn-1 + µn xn = θ . (6)

Relaţiei (6) îi aplicăm operatorul liniar U , U( xi ) = λi xi , i = 1 , … , n .
µ1 λ1 x1 + µ2 λ2 x2 + … + µn-1 λn-1 xn-1 + µn λn xn = θ (6’)
Înmulţim relaţia (6) cu ( -λn ) şi adunăm cu relaţia (6’) ⇒
µ1 ( λ1 – λn ) x1 + µ2 ( λ2 – λn ) + … + µn-1 ( λn-1 – λn ) xn-1 = θ ⇔ µ1 = µ2 =…= µn-1 =0
Din această ultimă relaţie şi din relaţia (6) rezultă că µn xn = θ . Cum xn ≠ 0 , înseamnă că µn =
0.
OBSERVAŢIE :
Dacă dim X = n şi operatorul U : X → X , U( xi ) = λi xi , ( i = 1, … , n ) , are n valori

proprii diferite , atunci { x1 , x2 , … , xn } formează o bază .
PROPOZIŢIA 4.5.3.
Fie U : X → X un operator liniar , dim X = n . Atunci valorile proprii ale operatorului U

sunt invariante la schimbarea bazelor .
DEMONSTRAŢIE :
Fie E = { e1 , e2 , … , en } o bază în spaţiul X .

Fie A matricea operatorului U : X → X corespunzătoare bazei E .
Fie G = { g1 , g2 , … , gn } o altă bază în spaţiul X .
Fie C matricea de trecere de la baza E la baza G.
⎧ g 1 = c11e1 + Κ + c1n en
⎪
⎨Μ
⎪g = c e + Κ + c e
⎩ n n1 1 nn n
Ecuaţia caracteristică este : | AT – λ I | = 0 .
B = CAC-1 ⇒ BT = (CT)-1 AT CT.
Ecuaţia caracteristică este : | BT – λ I | = 0 .
⇒ | (CT)-1AT CT – λ I | = | (CT)-1 AT CT – λ (CT)-1 CT | = | (CT)-1 AT CT - (CT)-1 λ CT | =

= | (CT)-1 ( AT – λ I ) CT | = | (CT)-1 | | AT – λ I | | CT | = | AT – λ I | = 0 .
CONSECINŢĂ :
Dacă operatorul U : X → X are n valori proprii diferite două câte două (spaţiul X
are dimensiunea n), atunci matricea operatorului U în baza { x1 , x2 , … , xn } unde U( xi ) = λi
xi , ( i = 1, … , n ) , este o matrice diagonală , având pe diagonală valori proprii .

DEMONSTRAŢIE :
Vectorul xi este un vector propriu corespunzător valorii proprii λi , ( i = 1, … , n ) .
λ1 ≠ λ2 ≠ λ3 ≠ … ≠ λn , λi ≠ λj , i ≠ j , i , j = 1, … , n .
U ( x1 ) = λ1 x1 = λ1 x1 + 0 x 2 + Κ + 0 x n ⎫ ⎛ λ1 0 0 Κ 0⎞
⎪ ⎜ ⎟
U ( x 2 ) = λ 2 x 2 = 0 x1 + λ 2 x 2 + Κ + 0 x n ⎪ ⎜ 0 λ2 0 Κ 0⎟
⎬⇒ A=⎜
Μ ⎪ Μ Μ Μ Κ Μ⎟
⎜⎜ ⎟
U ( x n ) = λn x n = 0 x1 + 0 x 2 + Κ + λn x n ⎪⎭ ⎝0 0 0 Κ λn ⎟⎠
Matricea A este matricea operatorului U în baza { x1 , x2 , … , xn } .
EXEMPLUL 2 :
⎛ x1 + 2 x 2 + x 3 ⎞
⎜ ⎟
U ( x) = ⎜ x3 ⎟
⎜ − x 3 ⎟⎠
Fie U : R 3 → R 3 , ⎝
⎛1 2 1 ⎞ 1− λ 2 1
⎜ ⎟
A = ⎜0 0 1 ⎟
T
A − λI = 0
T
−λ 1
⎜ 0 0 − 1⎟ − 1 − λ =( 1 – λ )( 1 + λ ) λ = 0 ⇒
⎝ ⎠ , 0 0
⎧λ1 = 1
⎪
⇒ ⎨λ2 = −1
⎪λ = 0
⎩ 3
pentru λ1 = 1 :
U( x ) = x ⇒ AT x = x
⎧ x1 + 2 x 2 + x 3 = x 1 ⎧2 x 2 + x 3 = 0
⎪ ⎪
⎨x3 = x2 ⇒ ⎨− x 2 + x 3 = 0
⎪− x = x
⎩ 3 3
⎪− 2 x = 0
⎩ 3 {
⇒ X λ1 = a (1,0,0) | a ∈ R
∗
}
pentru λ2 = - 1 :
U( x ) = - x ⇒ AT x = - x

⎧ x1 + 2 x 2 + x 3 = − x1
⎪ ⎧2 x 1 + 2 x 2 + x 3 = 0
⎨x3 = − x2 ⇒⎨
⎩x2 + x3 = 0
⎪− x = − x
⎩ 3 3 {
⇒ X λ2 = b(1,−2,2 ) | b ∈ R
∗
}
pentru λ3 = 0 :
U( x ) = 0 ⇒ AT x = 0
⎧ x1 + 2 x 2 + x 3 = 0
⎪ ⎧ x1 + 2 x 2 = 0
⎨x3 = 0 ⇒⎨
⎩x3 = 0
⎪− x = 0
⎩ 3 {
⇒ X λ3 = c(2,−1,0) | c ∈ R
∗
}
Fie x1 ∈ X λ1 , x1 = ( 1 , 0 , 0 ) .
⎧⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 2 ⎞ ⎫
⎪⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎪
G = ⎨⎜ 0 ⎟, ⎜ − 2 ⎟, ⎜ − 1⎟ ⎬
⎪⎜ 0 ⎟ ⎜ 2 ⎟ ⎜ 0 ⎟ ⎪
Fie x2 ∈ X λ2 , x3 = ( 1 , -2 , 2 ) . ⎩⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎭
Fie x3 ∈ X λ3 , x3 = ( 2 , -1 , 0 ) .
Calculăm matricea operatorului U în baza G :
U ( x 1 ) = 1 ⋅ x1 = 1 ⋅ x1 + 0 ⋅ x 2 + 0 ⋅ x 3 ⎫ ⎛1 0 0⎞
⎪ ⎜ ⎟
U ( x 2 ) = −1 ⋅ x 2 = 0 ⋅ x1 + (− 1) ⋅ x 2 + 0 ⋅ x 3 ⎬ ⇒ A = ⎜ 0 − 1 0 ⎟
U ( x 3 ) = 0 ⋅ x 3 = 0 ⋅ x1 + 0 ⋅ x 2 + 0 ⋅ x 3 ⎪ ⎜0 0 0⎟
⎭ ⎝ ⎠
IMPORTANŢA DIAGONALIZĂRII
Fie un polinom de gradul m , P ( λ ) = a0 + a1 λ +a2 λ2 + … +am λm .

Fie An ( K ) o matrice cu n linii şi n coloane .
P ( A ) = a0 In + a1 A +a2 A2 + … +am Am .
¾ Dacă A este o matrice diagonală :
⎛ λ1 0 Κ 0 ⎞ ⎛ λ12 0 Κ 0 ⎞
⎜ ⎟ ⎜ ⎟
⎜ 0 λ2 Κ 0 ⎟ ⎜ 0 λ2 Κ 0 ⎟
2
A=⎜ ⎟ A =⎜
2
⎟
Μ Ο Μ Ο
⎜⎜ ⎟ ⎜ ⎟
⎝0 0 Κ λm ⎟⎠ ⎜0 0
⎝ Κ λ2m ⎟⎠
Prin inducţie demonstrăm că :

⎛ λ1P 0 Κ 0 ⎞
⎜ ⎟
⎜ 0 λ2 Κ
P
0 ⎟
A =⎜
P
⎟
Μ Ο
⎜ ⎟
⎜ 0 Κ λmP ⎟⎠
⎝ 0
Fie matricea B , de forma :
⎛ µ1 0 Κ 0 ⎞ ⎛ λ1 + µ1 0 Κ 0 ⎞
⎜ ⎟ ⎜ ⎟
⎜ 0 µ2 Κ 0 ⎟ ⎜ 0 λ2 + µ 2 Κ 0 ⎟
B=⎜ ⎟ A+ B =⎜ ⎟
Μ Ο Μ Ο
⎜⎜ ⎟ ⎜⎜ ⎟
⎝0 0 Κ µ n ⎟⎠ ⎝ 0 0 Κ λn + µ n ⎟⎠
⎛ a0 Κ 0 ⎞ ⎛ a1 λ1 Κ 0 ⎞ ⎛ a 2 λ12 Κ 0 ⎞ ⎛ a n λ1n Κ 0 ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
P ( A) = ⎜ Ο ⎟+⎜ Ο ⎟+⎜ Ο ⎟ +Κ + ⎜ Ο ⎟=
⎜0 Κ
⎝
⎟ ⎜
a0 ⎠ ⎝ 0 Κ a n λ n ⎟⎠ ⎜⎝ 0 Κ a 2 λ2n ⎟⎠ ⎜ 0
⎝ Κ n ⎟
a n λn ⎠
⎛ a 0 + a1 λ1 + a 2 λ12 + Κ + a n λ1n Κ 0 ⎞ ⎛ P (λ1 ) Κ 0 ⎞

⎜ ⎟ ⎜ ⎟
=⎜ Ο ⎟=⎜ Ο ⎟
⎜ 0 Κ 2 n ⎟
a 0 + a1 λ n + a 2 λ n + Κ + a n λ n ⎠ ⎜⎝ 0 Κ P (λ n )⎟⎠
⎝
⎛ λ1 0⎞
⎜ ⎟
⎜ λ2 ⎟
A=⎜ ⎟
Ο
⎜⎜ ⎟
¾ Dacă A este o matrice diagonală , ⎝0 λn ⎟⎠ , atunci şi B este o matrice
diagonală , unde B = C-1AC .
DEMONSTRAŢIE :
B = C-1AC ⇒ A = CBC-1
A2 = CBC-1 CBC-1 = CB2C-1
Demonstrăm prin inducţie matematică faptul că An = CBnC-1 .
DEFINIŢIA 4.5.3.
Fie A ∈ Mn( K ) . Această matrice este diagonalizabilă dacă există o matrice C ,

C ∈ Mn( K ) , nesingulară , cu determinantul diferit de zero , şi există o matrice diagonală B astfel
încât A = C-1 B C .
DEFINIŢIA 4.5.4.
Matricele A şi B ∈ Mn( K ) se numesc similare dacă există o matrice C ∈ Mn( K )

astfel încât A = C-1 B C .
OBSERVAŢIE :
Relaţia de similitudine este o relaţie de echivalenţă .

DEFINIŢIA 4.5.5.
Fie (X,K) un spaţiu vectorial de dimensiune n , şi fie U : X → X un operator liniar .

Operatorul U este diagonalizabil dacă există în X o bază astfel încât matricea operatorului U în
baza E să fie o matrice diagonală .
⎛ a11 Κ 0 ⎞
⎜ ⎟
A=⎜ Ο ⎟
⎜ 0 Κ a nn ⎟⎠ .
U( XE ) = AT XE , ⎝
PROPOZIŢIA 4.5.4.
Fie U : X → X un operator liniar şi X λ = {x ∈ X | U ( x ) = λx} subspaţiul propriu

corespunzător valorii proprii λ . Atunci U ( X λ ) ⊂ x λ .
DEMONSTRAŢIE :
Fie y ∈U ( X λ ) ⇒ există x ∈ X λ astfel încât y = U( x ) .

Din x ∈ X λ rezultă că U( x ) = λ x . Deci y = λ x ⇒ y ∈ X λ .
OBSERVAŢIE :
Xλ este un invariant al operatorului U .
PROPOZIŢIA 4.5.5.
Fie U : X → X un operator liniar , dim X = n .
Fie x λ1 , x λ2 , Κ , x λ p subspaţii proprii corespunzătoare valorilor proprii λ1 ,

λ2 , … , λp , diferite două câte două ( λi ≠ λ j , i ≠ j, i, j = 1, Κ , p ) .
{
Fie E i = e i1 , ei2 , Κ , eini }∈ X λ i (i=1,…,p).
Atunci :
p
E = Υ Ei
1) i =1 este un sistem de vectori liniar independenţi .
⎡ p ⎤
x λi ∩ ∑ x λ j ⎥ = {θ }
⎢
⎢ j =1 ⎥
2) ⎣⎢ j ≠i ⎦⎥ .
DEMONSTRAŢIE :
1) x λ1 , {
E1 = e11 , Κ , e1n1 } sunt liniar independenţi .

x λ2 , E 2 = {e21 ,Κ , e2 n 2
} sunt liniar independenţi .
…………………………
x λ p , E p = {e p1 , Κ , e pn } sunt liniar independenţi .
p
⎛ ⎞ ⎛ ⎞ ⎛ ⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
θ = ⎜α 11 e11 + Κ + α 1n1 e1n1 ⎟ + ⎜α 21 e 21 + Κ + α 2 n2 e 2 n2 ⎟ + Κ + ⎜ α p1 e p1 + Κ + α pn p e pn p ⎟
⎜ 1 4 4 4 2x 4 4 4 3 ⎟ ⎜ 1 4 4 4 2x 4 4 4 3 ⎟ ⎜ 1 4 4 44 2x 4 4 4 43 ⎟
(1) ⎝ 1 ⎠ ⎝ 2 ⎠ ⎝ p ⎠
x i ∈ X λi ⎫⎪
⎬⇒
x1 + x 2 + Κ + x p = θ ⎪⎭ xi sunt vectori proprii sau xi = θ .
xi = θ este imposibil deoarece x i ∈ E i ⇒ x i ≠ θ .
x i = α i1 ei1 + Κ + α ini eini ⇒ {ei , ei ,Κ , ei

1 2 ni
} sunt vectori liniar independenţi ⇒ relaţia
(1) poate avea loc numai dacă αij = 0 .
p
x ∈∑ X λj ⇒
2) Fie x ∈ X λ1 şi x = x2 + … + xp , unde x 2 ∈ X λ2 , … , x p ∈ X λ p
j =1
j ≠i
⇒ x - x2 - … - xp = θ este o combinaţie liniară cu coeficienţi diferiţi de zero .
Întrucât x ∈ X λ1 , x2 , … , xp sunt liniar independenţi ( λi ≠ λ j , i ≠ j, i, j = 1, Κ , p ) ⇒
⇒ combinaţia liniară nu poate avea loc decât dacă x = θ .
OBSERVAŢIE:
x λi ∩ xλ j = θ , λi ≠ λ j .
Fie A ∈ Mn( K ) . Fie λ0 o valoare proprie corespunzătoare matricei A . Deci λ0 este

soluţie a ecuaţiei A − λ0 I = 0 .
DEFINIŢIA 4.5.6.
Dacă λ0 are ordinul de multiplicitate m , atunci “m” se numeşte ordinul de multiplicitate

algebrică.
DEFINIŢIA 4.5.7.
Fie dim X λ0 = r . Atunci “r “ se numeşte ordinul de multiplicitate geometrică.
PROPOZIŢIA 4.5.6.
Fie (X,K) un spaţiu vectorial , dim X = n . Fie U : X → X un operator liniar . Fie λ0 o

valoare proprie a operatorului U cu ordinul de multiplicitate algebrică m şi fie dim X λ0 = r .

Atunci : r ≤ m .
DEMONSTRAŢIE :
Fie E = { e1 , … , er } o bază în subspaţiul X λ0 . Completăm această bază în modul

următor : E = { e1 , … , er } ∪ { er+1 , … , en } , astfel încât E să fie bază în X .
U( ei ) = λ0 ei , i = 1 , … , r .
……………………………….
U( er+1 ) = ar+1,1 e1 + … + ar+1,r er + ar+1,r+1 er+1 + … + ar+1,n en
……………………………….
U( en ) = an1 e1 + … + anr er + anr+1 er+1 + … + ann en
⎛ λ0 0 Κ 0 a r +1,1 Κ a n1 ⎞
⎜ ⎟
⎜0 λ0 Κ 0 a r +1, 2 Κ an2 ⎟
⎜ Μ Μ Μ⎟
⎜ ⎟
AT = ⎜ 0 0 Κ λ0 a r +1,r Κ a nr ⎟
⎜0 0 Κ 0 a r +1, r +1 Κ a nr +1 ⎟
⎜ ⎟
⎜ Μ Μ Μ⎟
⎜0 0 Κ 0 a r +1,n Κ a nn ⎟⎠
⎝
⎛ λ0 − λ 0 Κ 0 a r +1,1 Κ a n1 ⎞
⎜ ⎟
⎜ 0 λ0 − λ Κ 0 a r +1, 2 Κ an2 ⎟
⎜ Μ Μ Μ ⎟
⎜ ⎟
A T − λI = ⎜ 0 0 Κ λ0 − λ a r +1,r − λ Κ a nr ⎟
⎜ Μ Μ ϕ (λ ) Μ ⎟
⎜ ⎟
⎜ 0 0 Κ 0 a r +1,n Κ a nn − λ ⎟
⎜ ⎟
⎝ ⎠
OBSERVAŢIE :
A este matricea operatorului U corespunzătoare bazei E completate astfel:
, … , e } . Ecuaţia caracteristică este : A − λI = 0 .
T
E ={ e , … , e } ∪ { e
1 r r+1 n
AT − λI = 0 ⇒ AT − λI = (λ0 − λ )r ϕ (λ ) = 0 ⇒ λ este o rădăcină multiplă de ordinul cel puţin

0
r . Deci : r ≤ m .
EXEMPLUL 3 :
⎛ x1 + x 2 ⎞ ⎛ x1 ⎞ ⎛1 1 0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
U (x ) = ⎜ x 2 + x 3 ⎟ x = ⎜ x2 ⎟ A = ⎜0 1 1⎟
T
⎜x ⎟ ⎜x ⎟ ⎜0 0 1⎟
U : R3 → R3 , ⎝ 3 ⎠ , ⎝ 3⎠ ⇒ ⎝ ⎠ .

1− λ 1 0
det AT − λI = 0 1− λ = (1 − λ ) = 0
3
1
0 0 1− λ ⇒ λ1 = λ2 = λ3 = 1 ⇒ m = 3 .
⎧⎛ a ⎞ ⎫
⎪⎜ ⎟ ⎪
x λ1=1 = ⎨⎜ 0 ⎟ | a ∈ R ⎬
⎪⎜ 0 ⎟ ⎪
U( x ) = 1*x ⇒ ⎩⎝ ⎠ ⎭ ⇒ r = dim X λ1 = 1 < 3 .
DEFINIŢIA 4.5.7.
Un corp K se numeşte algebric închis dacă o ecuaţie algebrică cu coeficienţi din K , de

gradul n , are n rădăcini în K .
PROPOZIŢIA 4.5.7.
Fie (X,K) un spaţiu vectorial , dim X = n , iar K este un corp algebric închis . Fie
U : X → X un operator liniar . Presupunem că U are valorile proprii :
λ1 multiplă de ordinul m1
⎛ p ⎞
⎜⎜ ∑ mi = n ⎟⎟
………………………….. ⎝ i =1 ⎠
λp multiplă de ordinul mp
Sunt echivalente afirmaţiile :
(1) U este un operator diagonalizabil .

(2) În X există o bază formată din vectorii proprii ai lui U .
(3) ri = mi ( i = 1 , … , p ) .
(4) X = X λ1 ⊕ X λ2 ⊕ Κ ⊕ X λ p .
DEMONSTRAŢIE :
¾ (1) ⇔ (2)
Din ipoteză este adevărat că U este diagonalizabil ⇒ există E = { e1 , … , en } o bază din X

astfel încât matricea operatorului U în această bază este diagonală .
⎛α 1 0⎞
⎜ ⎟
A=⎜ Ο ⎟
⎜0 α n ⎟⎠
⎝
U( e1 ) = α1 e1 ⇒ e1 ∈ X λ1
…………………………….. ⇒ În X există o bază formată din vectorii proprii ai
U( en ) = αn en ⇒ en ∈ X λn lui U .

¾ (2) ⇔ (3)
♦ Presupunem (2) adevarată : în X există o bază formată din vectorii proprii ai

operatorului U .
p
E = Υ Ei
i =1unde Ei este o mulţime formată din vectori liniar independenţi din spaţiul X λi , i
=1,…,p.
Cardinalul mulţimii Ei , notat card Ei , reprezintă numărul vectorilor din Ei .
card Ei ≤ ri ≤ mi
p p p p p
∑ cardEi ≤ ∑ ri ≤ ∑ mi = n n = cardE ≤ ∑ ri ≤ ∑ mi = n
i =1 i =1 i =1 ⇒ i =1 i =1 .
Această relaţie nu poate avea loc decât cu egalitate ⇒ ri = mi , i = 1 , … , p .
♦ Presupunem (3) adevărată : ri = mi , i = 1 , … , p .
Fie E i = {e i1 , Κ , e iri } o bază în spaţiul X λi , i = 1 , … , p . Vectorii din această bază sunt
vectori proprii din X λi şi sunt liniar independenţi .

p p p
E = Υ Ei ∑ ri = ∑ mi = n
i =1 deci i =1 i =1 ⇒ în X există o bază formată din vectorii proprii
ai operatorului U .
¾ (3) ⇔ (4)
Presupunem că ri = mi , i = 1 , … , p .
Din propoziţia 4.5.5. rezultă că [ ]

X λ1 ∩ X λ2 + X λ3 + Κ + X λ p = θ .
Deci este adevărat că X = X λ1 ⊕ X λ2 ⊕ Κ ⊕ X λ p .

Noţiunea de spaţiu vectorial

Vectori liniar independenţi şi liniar
dependenţi;bază şi dimensiune CAPITOLUL 5
Schimbarea coordonatelor unui
vector la schimbarea bazelor
Lema substituţiei
Spaţii vectoriale izomorfe
Subspaţii liniare FUNCŢIONALE PÃTRATICE
Sumă de subspaţii liniare
5.1. Noţiunea de funcţională pătratică
Fie (X,R) un spaţiu vectorial , dim X = n .
DEFINIŢIA 5.1.1.
Funcţia f : X → R este o funcţională liniară dacă oricare ar fi x1 , x2 care aparţin lui X şi

oricare ar fi α1 , α2 care aparţin lui R , atunci :
f ( α 1 x 1 + α 2 x 2 ) = α 1 f ( x1 ) + α 2 f ( x2 ) .
⎛ a1 ⎞
⎜ ⎟
A = ⎜Μ ⎟
⎜a ⎟
E = { e 1 , e 2 , … , en } ⎝ 2 ⎠ , ai = f ( ei ) , i = 1 , … , n .
Din capitolul 2 , subcapitolul “ Funcţionale biliniare “ , cunoaştem următoarele :
¾ Fie (X,R) , dim X = n şi fie (Y,R) , dim Y = m .

Funcţionala biliniară f : X × Y → R are proprietăţile :
1. Oricare ar fi α1 , α2 ∈ R , x1 , x2 ∈ X , y ∈ Y ,
f ( α1 x1 + α2 x2 , y ) = α1 f ( x1 , y ) + α2 f ( x2 , y ) .
2. Oricare ar fi β1 , β2 ∈ R , y1 , y2 ∈ Y , x ∈ X ,
f ( x ,β1 y1 + β2 y2 ) = β1 f ( x , y1 ) + β2 f ( x , y2 ) .
¾ f ( x, y ) = X ET AY G
În cazul în care Y = X , f : X × X → R . Atunci apar următoarele modificari :
A ( aij ) , aij = f ( ei , ej ) , i , j = 1 , … , n , f ( x, y ) = X T AY .
DEFINIŢIA 5.1.2.
Funcţionala biliniară f ( x , y ) este simetrică dacă f ( x , y ) = f ( y , x ) , oricare ar fi x , y

∈X.

DEFINIŢIA 5.1.3.
Prin diagonala produsului cartezian X × X înţelegem :
diagX × X = {( x, x ) | x ∈ X } .
DEFINIŢIA 5.1.4.
Se numeşte funcţională pătratică , restricţia unei funcţionale biliniare simetrice la

diagonala produsului cartezian X × X .
n n
V ( x ) = f ( x, x ) = X AX = ∑∑ a ij x i x j =
T
i =1 j =1 a11 x12 + 2 a12 x1 x2 + 2 a13 x1 x3 + … +
+ 2 a1n x1 xn + a22 x22 + 2 a23 x2 x3 + … + 2 a2n x2 xn + … + ann xn2 . ( aij = f ( ei , ej ) ) .
DEFINIŢIA 5.1.5.
V ( x ) este strict pozitiv definită dacă V ( x ) > 0 , oricare ar fi x ∈ X .
DEFINIŢIA 5.1.6.
V ( x ) este semipozitiv definită dacă V ( x ) ≥ 0 , oricare ar fi x ∈ X .
DEFINIŢIA 5.1.7.
V ( x ) este strict negativ definită dacă V ( x ) < 0 , oricare ar fi x ∈ X .
DEFINIŢIA 5.1.8.
V ( x ) este seminegativ definită dacă V ( x ) ≤ 0 , oricare ar fi x ∈ X .
DEFINIŢIA 5.1.9.
V ( x ) este nedefinită dacă există x ∈ X astfel încât V ( x ) ≥ 0 şi există y ∈ X astfel

încât V ( y ) ≤ 0 .
Se pune problema dacă există o bază G = { g1 , g2 , … , gn } astfel încât în această bază

( bază canonică ) , V ( x ) = β1 x12 + β2 x22 + … + βn xn2 .
5.2. Metoda Gauss pentru determinarea formei canonice a unei funcţionale

pătratice şi determinarea bazei
Fie (X,R) un spaţiu vectorial , dim X = n , E = { e1 , e2 , … , en } .

Fie f : X × X → R o funcţională biliniară simetrică .

A ( aij ) , aij = f ( ei , ej ) , i , j = 1 , … , n , f ( x, y ) = X T AY .
n n
V ( x ) = X T AX = ∑∑ a ij x i x j
i =1 j =1
Presupunem că există indicele i ( 1 ≤ i ≤ n ) astfel încât aii este diferit de zero. Presupunem că
a11 diferit de zero . Luăm separat termenii care conţin componenta x1 şi vom scrie astfel :
⎡ ⎛a a ⎞⎤
a11 ⎢ x12 + 2 x1 ⎜⎜ 12 x 2 + Κ + 1n x n ⎟⎟⎥
a11 x12 + 2 a12 x1 x2 + … + 2 a1n x1 xn = ⎣ ⎝ a11 a11 ⎠⎦ =
⎡⎛ a12 a1n ⎞
2
⎛ a12 a1n ⎞ ⎤
2
a11 ⎢⎜⎜ x1 + x2 + Κ + x n ⎟ − ⎜⎜ x2 + Κ + xn ⎟ ⎥
= ⎢⎣⎝ a11 a11 ⎟⎠ ⎝ a11 a11 ⎟⎠ ⎥ .
⎦
2
⎛ a a ⎞
V ( x ) = a11 ⎜⎜ x1 + 12 x 2 + Κ + 1n x n ⎟⎟ = V1 ( x )
Deci ⎝ a11 a11 ⎠ unde V1 ( x ) nu conţine pe x1 .
Notăm :
a12 a
y 1 = x1 + x 2 + Κ + 1n x n
a11 a11
y2 = x2
y3 = x3
Μ
yn = xn
Astfel , V ( y ) = a11 y12 + b22 y22 + 2 b23 y2 y3 + … + bnn yn2 .
Aplicăm acelaşi procedeu lui V1 şi după n paşi , obţinem forma canonică a funcţionalei .
Dacă aii = 0 , oricare ar fi i = 1 , … , n , vom face notaţia următoare :
x1 = y1 + y2 ; x2 = y1 – y2 ; x3 = y3 ; … ; xn = yn .
Astfel , vom obţine forma :
V ( x ) = a12 ( y1 + y 2 )( y1 − y 2 ) + ∑a ij y i y j = a12 y12 −a12 y 22 + ∑a ij yi y j

i≠ j i≠ j
i , j ≥3 i , j ≥3
EXEMPLUL 1 :
V ( x ) = 2 x12 + x22 – x32 + 6 x1 x2 – 8 x1 x3 + 2 x2 x3

2
2⎛ 7 ⎞
V ( x ) = (2 x1 + 3x 2 − 4 x 3 ) − ⎜ − x 2 + 7 x 3 ⎟ + 5 x 3
1 2
2 7⎝ 2 ⎠

y 1 = 2 x1 + 3 x 2 − 4 x 3
7
y2 = − x2 + 7 x3
2
V ( y ) = y12 − y 22 + 5 y 32
1 2
y3 = x3 ⇒ (1) 2 7 ,
reprezintă o funcţională în forma canonică .
Care este baza din spaţiul vectorial X în care funcţionala pătratică V are forma
canonică (1) ?
⎛ y1 ⎞ ⎛⎜ 2 3 − 4 ⎞⎛ x 1 ⎞
⎟⎜ ⎟
⎜ ⎟ 7
⎜ y2 ⎟ = ⎜ 0 − 7 ⎟⎜ x 2 ⎟
⎜y ⎟ ⎜ 2 ⎟⎜ ⎟
⎝ 3 ⎠ ⎝0 0 1 ⎠⎝ x 3 ⎠
Y = (C T ) X , unde C ( c ) este matricea de trecere de la baza E la baza G ( G este baza în

−1
ij
care funcţionala pătratică are forma canonică ) .
⎛1 3 ⎞ ⎛ 1 ⎞
⎜ − 1⎟ ⎜ 0 0⎟
⎜2 7 ⎟ ⎜ 2 ⎟
⎛2 3
⎜
− 4⎞
⎟ ((C ) )
T −1
−1
= CT = ⎜ 0 −
2
2 ⎟ ⇒ C EG = ⎜
3
−
2
0⎟
(C )
T −1
= ⎜0 −
7
7 ⎟ ⎜
⎜0 0
7 ⎟
1 ⎟
⎜ 7
⎜−1 2
7 ⎟
1⎟
⎜ 2 ⎟ ⎜ ⎟ ⎜ ⎟
⎝0 0 1 ⎠ ; ⎝ ⎠ ⎝ ⎠
Fie baza G baza în care vom determina forma canonică a funcţionalei pătratice V ,
G = { g1 , g2 , … , gn }
Calculăm vectorii acestei baze :

⎛1⎞
⎛1⎞ ⎜ 2 ⎟
1 1⎜ ⎟ ⎜ ⎟
g 1 = c11 e1 + c12 e 2 + c13 e3 = e1 = ⎜ 0 ⎟ = ⎜ 0 ⎟
2 2⎜ ⎟
⎝ 0 ⎠ ⎜⎜ 0 ⎟⎟
⎝ ⎠
⎛ 3 ⎞
⎜ ⎟
⎜ 7 ⎟
3 2 2
g 2 = e1 − e 2 = ⎜ − ⎟ ⎛ − 1⎞
7 7 ⎜ 7⎟ ⎜ ⎟
⎜ 0 ⎟ g 3 = −e1 + 2e 2 + e3 = ⎜ 2 ⎟
⎜ ⎟ ⎜ 1⎟
⎝ ⎠ ⎝ ⎠

⎛1 ⎞
⎜ 0 0⎟
⎜2 ⎟
2
B=⎜0 − 0⎟
⎜ 7 ⎟
⎜0 0 5⎟
⎜ ⎟
Matricea B a funcţionalei V în baza G este : ⎝ ⎠ .
5.3. Metoda Jacobi pentru determinarea formei canonice a funcţionalei

pătratice
V ( x ) = 2 x12 + x22 – x32 + 6 x1 x2 – 8 x1 x3 + 2 x2 x3
2 3 −4
2 3 ∆3 = 3 1 1 = −35
∆2 = = −7
Notăm : ∆ 0 = 1 , ∆ 1 = 2 , 3 1 , −4 1 −1 .
∆ 0 2 ∆1 2 ∆ 2 2
V (y) = y1 + y2 + y3
∆1 ∆2 ∆3
V (y) =
1 2 2 2 1 2
y1 − y 2 + y 3
Deci , obţinem : 2 7 5 .
Într – un spaţiu există mai multe baze în care funcţionala poate fi adusă la forma
canonică , deci forma canonică obţinută prin metoda Gauss diferă de cea obţinută prin metoda
Jacobi .
Metoda Jacobi se poate aplica numai dacă toţi minorii principali ai matricei A sunt
nenuli .
METODA JACOBI LA CAZUL GENERAL
Fie spaţiul vectorial (X,R) , dim X = n , E = { e1 , e2 , … , en } .

Fie f : X × X → R o funcţională biliniară simetrică .
Fie A( aij ) matricea funcţionalei f în baza E .
TEOREMA 5.3.1.
n n
V ( x ) = x T Ax = ∑∑ a ij x i x j
Fie i =1 j =1 o funcţională pătratică , unde A( aij ) este matricea
funcţionalei V în baza E . Dacă toţi minorii principali ai matricei A sunt nenuli ,
a11 Κ a1r
∆r = Μ Μ≠0
a r1 Κ a rr ( r = 1 , … ,n ) şi ∆ 0 = 1 ,
atunci există o bază G = { g1 , g2 , … , gn } în care matricea B a funcţionalei V este diagonală şi

⎛ ∆0 ⎞
⎜ 0 ⎟
⎜ ∆1 ⎟
⎜ ∆1 ⎟
B=⎜ ∆2 ⎟
⎜ ⎟
⎜ Ο ⎟
⎜ 0 ∆ n −1 ⎟
⎜ ∆ n ⎟⎠ .
⎝
OBSERVAŢIE :
n
∆ i −1 2
V (y) = ∑ yi
În baza G , i =1 ∆n .
DEMONSTRAŢIE :
Vom construi baza G astfel :
g1 = λ11 e1
g2 = λ21 e1 + λ22 e2
…………………..
(1) gi = λi1 e1 + λi2 e2 + … + λii ei
………………………………
gn = λn1 e1 + λn2 e2 + … + λnn en
Vom determina scalarii λij din condiţiile :
⎧ f ( g k , ei ) = 0
⎨
(2) ⎩ f (g k , e k ) = 1 k = 1 , … , n , i = 1 , … ,k-1
k=1
f( g1 ,e1 ) = 1 ⇒ f( λ11 e1 , e1 ) = 1 ⇒ λ11 f( e1 , e1 ) = 1 ⇒ λ11 a11 = 1 ⇒
1
λ11 =
⇒ a11 . ( din ipoteză , a11 este diferit de zero ) .
k=2
⎧ f (g 2 , e1 ) = 0 ⎧ f (λ21 e1 + λ22 e 2 , e1 ) = 0 ⎧λ21 f (e1 , e1 ) + λ22 f (e 2 , e1 ) = 0
⎨ ⇒⎨ ⇒⎨ ⇒
⎩ f (g 2 , e 2 ) = 1 ⎩ f (λ21 e1 + λ22 e 2 , e 2 ) = 1 ⎩λ21 f (e1 , e 2 ) + λ22 f (e 2 , e 2 ) = 1
⎧a11 λ21 + a 21 λ22 = 0 ⎧a11 λ21 + a 21 λ22 = 0

⎨ ⎨
⇒ ⎩a12 λ21 + a 22 λ22 = 1 ⇒ ⎩a 21 λ21 + a 22 λ22 = 1
a12 = a21

0 a 21 0 a 21 0 a 21
1 a 22 1 a 22 1 a 22 a11 0
λ21 = = =
a11 a 21 a11 a12 ∆2 a12 1 ∆ 22
λ22 = =
a12 a 22 a 21 a 22 , ∆2 ∆2 .
Analog demonstrăm şi pentru 1 ≤ k ≤ n , iar sistemul (2) are soluţia următoare :
col1 Κ coli Κ colk

a11 Κ 0 Κ a1k
∆ ki Μ Μ Μ
λ ki =
∆k , unde ∆ ki = a k1 Κ 1 Κ a kk
În baza G astfel determinată , matricea B a funcţionalei pătratice V este de forma:

⎛ ∆0 ⎞
⎜ 0 ⎟
⎜ ∆1 ⎟
⎜ ∆1 ⎟
B= ⎜ ∆2 ⎟
⎜ ⎟ ⎧0, i ≠ j
⎜ Ο ⎟ ⎪
⎜ 0 ∆ n −1 ⎟ bij = ⎨ ∆ i −1
⎜ ∆ n ⎟⎠ ⎪ ∆ ,i = j .
⎝ , ⎩ i
¾ pentru i < j :
bij = f( gi , gj ) = f( λi1 e1 + … + λii ei , gj ) = λi1 f( e1 , gj ) + … +
+ λii f( ei , gj ) = λi1 f( gj , e1 ) + … + λii f( gj , ei ) .
Din sistemul (2) , rezultă că pentru i < j , bij = 0 .
¾ pentru i = j :
bii = f( gi , gj ) = f( λi1 e1 + … + λii-1 ei-1 + λii ei , gi ) =
λi1 f (e1 , g i ) + Κ + λii −1 f (ei −1 , g i ) + λii f (ei , g i ) = λii

1 42 43 1 4 4 2 4 43 1 42 43
= =0 =0 =1 .
a11 Κ a1,i −1 0
Μ Μ Μ ∆
∆ ii = = ∆ i −1 ⇒ λii = i −1
∆ ii a i −1,1 Κ a i −1,i −1 0 ∆i
λii =
∆i , a i1 Κ a i ,i −1 1 .
EXEMPLUL 1 :
V ( x ) = 2 x12 + x22 – x32 + 6 x1 x2 – 8 x1 x3 + 2 x2 x3

⎛ 2 3 − 4⎞
⎜ ⎟
A=⎜ 3 1 1 ⎟
⎜− 4 1 1 ⎟
⎝ ⎠
2 3 −4
2 3 ∆ 3 = 3 1 1 = −35
∆2 = = −7
∆ 0 = 1 , ∆1 = 2 , 3 1 , − 4 1 −1
∆ 0 2 ∆1 2 ∆ 2 2
V (y) = y1 + y2 + y3 V ( y ) = y12 − y 22 + y 32
1 2 1
∆1 ∆2 ∆3 ⇒ 2 7 5
g1 = λ11 e1
g2 = λ21 e1 + λ22 e2
g3 = λ31 e1 + λ32 e2 + λ33 e3
¾ pentru k = 1 :
⇒ f( g1 , e1 ) = 1 ⇒ f( λ11 e1 , e1 ) = λ11 f( e1 , e1 ) = λ11 a11 = 2λ11 = 1 ⇒

⎛1⎞
⎜ ⎟
⎜2⎟
g1 = ⎜ 0 ⎟
1 1 ⎜0⎟
g 1 = e1 ⎜ ⎟
⇒ λ11 = 2 ⇒ 2 ⇒ ⎝ ⎠ .
¾ pentru k = 2 :
⎧ f (g 2 , e1 ) = 0 ⎧ f (λ21 e1 + λ22 e 2 , e1 ) = 0 ⎧λ21 a11 + λ22 a 21 = 0

⎨ ⇒⎨ ⇒⎨ ⇒
⇒ ⎩ f (g 2 , e 2 ) = 1 ⎩ f (λ21 e1 + λ22 e 2 , e 2 ) = 1 ⎩λ21 a12 + λ22 a 22 = 1
⎛ 3 ⎞
⎜ ⎟
⎧ 3 ⎜ 7 ⎟
⎪ λ 21 = 2
g2 = ⎜ − ⎟
⎧2λ 21 + 3λ22 = 0 ⎪ 7 ⎜ 7⎟
⎨ ⇒⎨ ⇒
λ
⎩ 21
3 + λ = 1 2 ⎜ 0 ⎟
22 ⎪λ 22 = − g =
3
e −
2
e ⇒ ⎜ ⎟
⇒ ⎪⎩ 7 2
7
1
7
2
⎝ ⎠
¾ pentru k = 3 :
⎧ f (g 3 , e1 ) = 0 ⎧ f (λ31 e1 + λ32 e 2 + λ33 e3 , e1 ) = 0

⎪ ⎪
⎨ f (g 3 , e 2 ) = 0 ⇒ ⎨ f (λ31 e1 + λ32 e 2 + λ33 e3 , e 2 ) = 0 ⇒
⎪ ⎪ f (λ e + λ e + λ e , e ) = 1
⇒ ⎩ f (g 3 , e1 ) = 1 ⎩ 31 1 32 2 33 3 3

⎧ 1
⎪ λ 31 = −
⎧λ31 a11 + λ32 a 21 + λ33 a 31 = 0 ⎧2λ31 + 3λ32 − 4λ33 = 0 ⎪ 5
⎪ ⎪ ⎪ 2
⇒ ⎨λ31 a12 + λ32 a 22 + λ33 a 32 = 0 ⇒ ⎨3λ31 + λ32 + λ33 = 0 ⇒ ⎨λ32 = −
⎪λ a + λ a + λ a = 1 ⎪ − 4λ + λ − λ = 1 ⎪ 7
⎩ 31 13 32 23 33 33 ⎩ 31 32 33
⎪ 1
⎪⎩λ33 = 5
⇒
1 2 1
g 3 = − e1 − e 2 + e3
⇒ 5 7 5 .
Matricea B a funcţionalei pătratice V are forma :
⎛1 ⎞
⎜ 0⎟
⎜2 ⎟
2
B=⎜ − ⎟
⎜ 7 ⎟
⎜ 1⎟
⎜0 ⎟
⎝ 5⎠
5.4. Legea inerţiei
TEOREMA 5.4.1.
Numărul coeficienţilor pozitivi şi numărul coeficienţilor negativi din forma canonică a

unei funcţionale pătratice V( x ) nu depinde de alegerea bazei canonice .
( Deci , coeficienţii pozitivi şi coeficienţii negativi sunt invarianţi ai funcţionalei pătratice .)
DEMONSTRAŢIE :
Fie spaţiul vectorial (X,R) , dim X = n .Fie bazele canonice E şi G din spaţiul vectorial X ,
astfel încât :
E = { e1 , e2 , … , en } xE = ( x1 , x2 , … , xn )T
G = { g1 , g2 , … , gn } yG = ( y1 , y2 , … , yn )T
m1 n1
V ( x ) = ∑ λi x −
2
i ∑λ j x 2j
În baza E : i =1 j = m1+1 , λi > 0 , i = 1 , … , m1
λj > 0 , j = m1+1 , … , n1
m2 n2
V ( y ) = ∑ µ i y i2 − ∑µ j y 2j
În baza G : i =1 j = m 2 +1 , µi > 0 , i = 1 , … , m2
µj > 0 , j = m2+1 , … , n2
Deci funcţionala pătratică are în baza E , m1 coeficienţi pozitivi şi n1 – m1 coeficienţi

negativi . ( Nu am scris n ci n1 , pentru că există posibilitatea ca anumiţi coeficienţi să fie nuli . )
Trebuie să demonstrăm că m1 = m2 şi n1 = n2 .
Demonstraţia o vom face prin reducere la absurd . Presupunem contrariul şi anume m1

> m2 .
Fie subspaţiul X1 = Sp ( { e1 , … , em1 } ) , X1 ⊂ X , dim X1 = m1 .
Fie subspaţiul X2 = Sp ( { gm2+1 , … , gn } ) , X2 ⊂ X , dim X2 = m1 .
Fie D = X 1 ∩ X 2 .
dim X1 + dim X2 = m1 + n – m2 ⇒ D conţine şi vectori nenuli .
m1 n
x ∈ D ⇒ x ∈ X 1 ⇒ x = ∑ x i ei x∈ X2 ⇒ x = ∑ y jg j
1 4 2i =1 4 3 1 44j =2m 2 +41 43
Fie ⇓ , ⇓
() ( ) ∑y
m1 n
V x = ∑ λi x i2 > 0 V x = j y 2j < 0
i =1 j = m 2 +1
() ()
Dar V x > 0 şi V x < 0 este absurd . Astfel , rezultă că m1 ≤ m2 .
⇒ m1 = m2 .
Analog , presupunând că m1 < m2 , obţinem m1 ≥ m2 .
Asemănător demonstrăm că n1 = n2 .
DEFINIŢIA 5.4.1.
Se numeşte indice de inerţie a formei pătratice V ( rangul formei pătratice V ) , numărul

total de termeni ce apar într – o formă canonică .
DEFINIŢIA 5.4.2.
m1 = m2 se numeşte indicele pozitiv de inerţie al funcţionalei pătratice V

( adică numărul termenilor pozitivi dintr – o formă canonică ) .
DEFINIŢIA 5.4.3.
n1 = n2 se numeşte indicele negativ de inerţie al funcţionalei pătratice V .
OBSERVAŢIE :
Dacă m1 = n1 , atunci toţi coeficienţii funcţionalei pătratice V în forma
canonică sunt pozitivi , deci funcţionala V este pozitiv definită .
REGULA LUI SYLVESTER :
Pentru ca o matrice simetrică A( aij ) să determine o funcţională pătratică pozitiv definită ,

este necesar şi suficient ca toţi minorii principali ∆ r să fie strict pozitivi .
a11 Κ a 1r
∆r = Μ Μ>0
a r1 Κ a rr r=1,…,n .


CAPITOLUL 6
SPAŢII NORMATE . SPAŢII METRICE
6.1. Normă ; distanţă
Fie (X,K) un spaţiu vectorial , dim X = n , K = R sau K = C .
DEFINIŢIA 6.1.1.
|| • ||: X → K se numeşte normă dacă :
1) || x || ≥ 0 , oricare ar fi x ∈ X , || x || = 0 ⇔ x = θ
2) || α x || = | α | || x || , oricare ar fi x ∈ X , α ∈ K
3) || x + y || ≤ || x || + || y || , oricare ar fi x , y ∈ X
DEFINIŢIA 6.1.2.
Un spaţiu vectorial peste care s – a definit o normă se numeşte spaţiu vectorial normat .
EXEMPLUL 1 :
X = Rn , K = R
n
|| x || =
x, x = ∑x
i =1
2
i
, x ∈ R , x = ( x 1 , … , xn ) T .
Fie X o mulţime nevidă . ( X poate fi şi un spaţiu vectorial )
DEFINIŢIA 6.1.3.
d : X × X → R se numeşte metrică sau distanţă , dacă :
1) d( x , y ) = d( y , x ) , oricare ar fi x , y ∈ X
2) d( x , y ) ≥ 0 , oricare ar fi x , y ∈ X şi d( x , y ) = 0 ⇔ x = y
3) d( x , y ) ≤ d( x ,z ) + d( z , y ) , oricare ar fi x , y , z ∈ X
n
d ( x, y ) =|| x − y ||= x − y, x − y = ∑ (x − yi )
2
i
EXEMPLUL 2 : i =1
6.2. Operatori ortogonali
Fie (X,K) un spaţiu euclidian , dim X = n , iar U : X → X un operator liniar .

DEFINIŢIA 6.2.1.
Operatorul U este ortogonal dacă < U( x ) , U ( y ) > = < x , y > , oricare ar fi x ,y ∈ X .
Fie E = { e1 , e2 , … , en } o bază ortonormală în spaţiul vectorial X .
ei ⊥e j , < e , e > = 0 , oricare ar fi i ≠ j , i , j = 1 , … , n

i j
< ei , ei > = 1 , deci || ei || = 1 , oricare ar fi i , j = 1 , … , n
Din relaţiile de mai sus obţinem :

⎧1, i = j
⎨
< ei , ej > = δij = ⎩0, i ≠ j .
OBSERVAŢIE :
Conform teoremei Gramm–Schmidtt , dintr–o bază oarecare se poate obţine o bază

ortogonală . Împărţind fiecare vector al acestei baze ortogonale cu propria sa normă obţinem o
bază ortonormală .
TEOREMA 6.2.1.
Fie (X,R) un spaţiu euclidian , dim X = n . Fie E = { e1 , e2 , … , en } o bază ortonormală .

Fie U : X → X un operator ortogonal şi fie A( aij ) matricea operatorului U în baza E . Atunci :
A·AT = AT ·A = In .
DEMONSTRAŢIE :
Din ipoteză ştim că baza E = { e1 , e2 , … , en } este ortonormală , deci vectorii bazei E

verifică relaţia : < ei , ej > = δij , oricare ar fi i , j = 1 , … , n .
A(a ij ) ⇒ ei = ∑ a ik e k
n n
e j = ∑ a jm e m
k =1 ( vezi definiţia matricei unui operator ) , m =1 .
Din ipoteză , U : X → X este ortogonal ⇒ < U( x ) , U ( y ) > = < x , y > , oricare ar fi

x ,y ∈ X .
< U (ei ), U (e j ) >=< ei , e j >=< ∑ a ik e k , ∑ a jm e m >= ∑∑ a ik a jm < e k , e m >=

n n n n
k =1 m =1 k =1 m =1
n n n n n
= ∑ ∑ a ik a jm δ km = ∑ a ik a jk δ kk = ∑ a ik a kjT = A ⋅ AT = I n ∑a ik a jk = δ ij
k =1 m =1 k =1 k =1 , k =1 .
TEOREMA 6.2.2.
Fie (X,R) un spaţiu euclidian , dim X = n . Fie E = { e1 , e2 , … , en } o bază ortonormală .

Fie U : X → X un operator ortogonal . Fie A matricea operatorului U în baza E . Atunci :
1) Operatorul U conservă norma .
2) Operatorul U conservă distanţa dintre doi vectori ( U este izometric ) .
3) Valorile proprii reale ale operatorului U sunt “ + 1 “ sau “ – 1 “ .

DEMONSTRAŢIE :
1) ||U ( x ) ||= < U ( x ), U ( x ) > = < x, x > =|| x || .
2) d( U( x ) , U( y ) ) = || U( x ) – U( y ) || = || U( x – y ) || = || x – y || = d( x , y )
3) Fie λ ∈ R o valoare proprie a operatorului U , deci U( x ) = λ x ⇒
< U ( x ), U ( x ) >=< λx, λx >= λ2 < x, x > ⎫ λ2 < x, x >=< x, x > ⎫

⎬⇒ ⎬ ⇒ λ = 1 ⇒ λ = ±1
2
⇒ U ortogonal ⇒< U ( x ), U ( x ) >=< x, x > ⎭ x ≠ θ ⇒< x, x >> 0 ⎭
EXEMPLUL 1 : Operatori ortogonali pe spaţii unidimensionale :
Fie X un spaţiu euclidian , dim X = n . Fie E = { e } o bază a lui X . Fie U : X → X un

operator ortogonal .
Din teorema 6.2.2. rezultă că λ1 = 1 , λ2 = -1 , deci U( e ) = 1·e şi U( e ) = -1·e
EXEMPLUL 2: Operatori ortogonali pe spaţii bidimensionale :
Fie X un spaţiu euclidian real , dim X = 2 . Fie E = { e1 , e2 } o bază în X . Fie U : X → X

un operator ortogonal . ( E este o bază ortonormală. )
⎛a b ⎞
A = ⎜⎜ ⎟⎟
Fie A matricea operatorului U în baza E , ⎝c d ⎠ .
Din teorema 6.2.1. rezultă că | A | = ± 1
| A | = 1 ⇒ ad – cb = 1 ⇒ | AT | = 1
⎛a c ⎞ ⎫
AT ⋅ A = I 2 ⇒ AT = A −1 ⇒ A −1 = ⎜⎜ ⎟⎟ ⎪
⎝b d ⎠ ⎪ ⎧a = d ⎛a − c⎞
⎬⇒⎨ ⇒ A = ⎜⎜ ⎟⎟
−1 1 ⎛ d − b ⎞ ⎛ d − b ⎞ ⎛ a c ⎞ ⎪ ⎩b = − c ⎝c a ⎠
A = ⎜ ⎟=⎜ ⎟=⎜ ⎟
det A ⎜⎝ − c a ⎟⎠ ⎜⎝ − c a ⎟⎠ ⎜⎝ b d ⎟⎠ ⎪⎭
det A = 1 ⇒ a2 + c2 = 1 ⇒ există un unghi φ astfel încât a = cos φ şi c = sin φ .
⎛ cos ϕ − sin ϕ ⎞
⇒ A = ⎜⎜ ⎟
⎝ sin ϕ cos ϕ ⎟⎠
6.3. Operatori autoadjuncţi
Fie (X,R) , K = R sau K = C , un spaţiu euclidian .

Fie U : X → X un operator liniar .

DEFINIŢIA 6.3.1.
Operatorul U este autoadjunct dacă < U( x ) , y > = < x , U( y ) > , oricare ar fi vectorii x ,
y ∈ X.
PROPOZIŢIA 6.3.1.
Fie (X,C) un spaţiu euclidian , dim X = n , U : X → X un operator autoadjunct. Atunci : <

U( x ) , y > ∈ R , oricare ar fi x , y ∈ X .
DEMONSTRAŢIE :
< U( x ) , y > = < x , U( y ) > = < U ( x ), y > ⇒ < U( x ) , y > ∈ R .
PROPOZIŢIA 6.3.2.
Dacă operatorul U : X → X este autoadjunct , atunci valorile sale proprii sunt reale .
DEMONSTRAŢIE :
Fie λ o valoare proprie a operatorului U ⇒ U( x ) = λ x .
< U ( x
1 4 2 43
), x > =< λx , x >= λ < x , x >= λ || x ||2
∈R ⇒ λ∈R
∈R , deoarece || x ||2 este real .
PROPOZIŢIA 6.3.3.
Fie U : X → X un operator autoadjunct . Fie λ1 , λ2 două valori proprii reale diferite .

Fie X λ1 şi X λ2 subspaţiile proprii corespunzătoare valorilor proprii λ1 şi λ2 . Atunci X λ1 ⊥X λ2 .
DEMONSTRAŢIE :
Fie x ∈ X λ1 ⇒ U( x ) = λ1 x , x ≠ θ .
Fie y ∈ X λ2 ⇒ U( y ) = λ2 y , y ≠ θ . ( λ 2 ∈ R ⇒ λ 2 = λ 2 )
< U( x ) , y > = < x , U( y ) > ⇒ < λ1 x , y > = < x , λ2 y > ⇒ λ1 < x , y > = λ2 < x , y > ⇒ λ1 <
x , y > = λ2 < x , y > ⇒ ( λ1 – λ2 ) < x , y > ⇒ λ1 ≠ λ2 ⇒ < x , y > = 0 ⇒
⇒ x⊥y ⇒ X λ1 ⊥X λ2 .
MATRICE HERMITIANĂ
Fie A ∈ M n (C ) , aij ∈ C , i , j = 1 , … , n .
*
( )
Fie A a ij ∈ M n (C ) , a ij = a ij .
* *
DEFINIŢIE :

Dacă A = A* , atunci matricea A se numeşte matrice hermitiană .
EXEMPLUL 1 :
⎛ 1 1 − 2i ⎞ ⎛ 1 1 + 2i ⎞ ⎛ 1 1 − 2i ⎞
A = ⎜⎜ ⎟ A* = ⎜⎜ ⎟ = ⎜⎜
⎟ ⎟⎟ ⇒ A = A*
⎝1 + 2i 5 ⎟⎠ ⎝1 − 2i 5 ⎠ ⎝ 1 + 2i 5 ⎠ .
OBSERVAŢIE : dacă A este o matrice de numere reale , atunci A = A* dacă A = AT.
TEOREMĂ :
Fie (X,C) un spaţiu euclidian , dim X = n . Fie U : X → X un operator autoadjunct . Fie E

= { e1 , e2 , … , en } o bază ortonormală . Fie A( aij ) matricea operatorului U corespunzătoare
bazei E . Atunci A este o matrice hermitiană .
6.4. Metoda transformărilor ortogonale pentru determinarea formei canonice a

unei funcţionale pătratice
Fie (X,R) un spaţiu euclidian , dim X = n , iar E = { e1 , e2 , … , en } o bază în

spaţiul X .
Fie A( aij ) matricea funcţionalei f : X × X → R o funcţională biliniară simetrică .
n n
V ( x ) = f ( x, x ) = x T Ax =< x T A, x >= ∑∑ a ij x i x j
i =1 j =1 , x = ( x1 , … , xn )T .
A este o matrice simetrică ⇒ A = AT ⇒ U( x ) = AT x = A x = λ x .

U este un operator autoadjunct ⇒ U( x ) = A x = xT AT = xT A .
V( x ) = f( x , x ) = < xT A , x > = < U( x ) , x >
Presupunem că det A este diferit de zero .

Ştim că U are valori proprii reale distincte ⇒ X λ1 ⊥X λ2 ⊥ Κ ⊥X λn .
g 1 ∈ X λ1 ⇒ U (g 1 ) = λ1 g 1 ⎫
⎪
Μ ⎬ ⇒ G = {g 1 , Κ , g n }
g n ∈ X λn ⇒ U (g n ) = λ n g n ⎪⎭ formează o bază ortogonală .
Fie B matricea operatorului U în baza G , B( bij ) i , j = 1 , … , n .
bij = f < g i , g j >=< U (g i ), g j >=< λi g i , g j >= λi < g i , g j >= λi || g i ||2 , unde i , j = 1 ,

…,n .
Considerăm baza ortonormală H = { h1 , h2 , … , hn } .

g1 g
h1 = , Κ , hn = n
|| g 1 || || g n ||
Fie D matricea operatorului U corespunzătoare bazei H .
⎛ g ⎞ gj λi λ
d ij = f (hi , h j ) =< U (hi ), h j >=< U ⎜⎜ i ⎟⎟, >= < g i , g j >= i2 || g i2 || δ ij =
⎝ || g i || ⎠ || g j || || g i |||| g j || || g i ||
= λi δ ij .
n
V ( x ) = ∑ α i2 λi
xH = ( α1 , … , αn ) T , i =1 .
EXEMPLUL 1 :
Să se determine forma canonică a funcţionalei pătratice

V ( x ) = x12 + x 22 + x 32 + x1 x 2 + x1 x 3 + x 2 x 3
prin metoda transformărilor ortogonale .
⎛ 1 1⎞
⎜1 ⎟
⎜ 2 2⎟
1 1⎟
A=⎜ 1
⎜2 2⎟
⎜1 1 ⎟
⎜ 1⎟
⎝2 2 ⎠
Fie U : R 3 → R 3 , U este operatorul care are ca matrice pe A în baza canonică .
⎛ ⎞
U ( x ) = ⎜ x1 + x 2 + x 3 , x1 + x 2 + x 3 , x1 + x 2 + x 3 ⎟
1 1 1 1 1 1
⎝ 2 2 2 2 2 2 ⎠
Calculăm valorile proprii ale matricei A .
1 1 1 1 1 1
1− λ 2−λ 1
2 2 2 2 2 2
= (2 − λ )1 1 − λ
1 1 1 1
A − λI = 1− λ = 0 ⇔ 2 − λ 1− λ =
2 2 2 2
1 1 1 1
1− λ 2−λ 1− λ 1 1− λ
2 2 2 2
1 1
1
2 2 2
⎛1 ⎞
= (2 − λ ) 0 = (2 − λ )⎜ − λ ⎟
1
−λ 0
2 ⎝2 ⎠
1
0 0 −λ λ2 = λ3 =
1
2 ⇒ λ1 = 2 , 2 .

Calculăm subspaţiile proprii corespunzătoare acestor valori proprii .
X λ1 = {x ∈ R 3 | U ( x ) = 2 x, x ≠ θ } ⇒ X λ1 = {x = (a , a , a ) | a ∈ R \ {0}}
⎧ ⎫
X λ2 = ⎨ x ∈ R 3 | U ( x ) = x , x ≠ θ ⎬
1
⎩ 2 {
⎭ ⇒ X λ2 = x = (a, b,−a − b ) | a, b ∈ R, a + b ≠ 0
2 2
}
Considerăm baza B = { b1 , b2 , b3 } , b1 ∈ X λ1 b2 , b3 ∈ X λ2 .
Fie b1 = ( 1 , 1 , 1 ) ( a = 1 )
b2 = ( 1 , 0 , -1 ) ( a = 1 , b = 0 )
b3 = ( 0 , 1 , -1 ) ( a = 0 , b = 1 )
{ b1 , b2 , b3 } este o bază ce trebuie ortogonalizată prin teorema Gramm–Schmidtt .
⎧h1 = b1 ⎛ 1⎞
⎪ ⎜ ⎟
⎨h2 = b2 + αb1 h1 = ⎜1⎟
⎪h = b + βb + γb ⎜ 1⎟
⎩ 3 3 2 1 ⎝ ⎠ .
< h2 , h1 > = 0 ⇔ < b2 +α b1 , b1 > = < b2 , b1 > + α < b1 , b1 > = 0

< b2 , b1 > = 0 ⇒ < b1 , b1 > = 3 ⇒ 3α = 0 ⇒ α = 0 .
⎛ 1⎞
⎜ ⎟
α = 0 ⇒ h2 = b2 = ⎜ 0 ⎟
⎜ − 1⎟
⎝ ⎠
⎛ 1⎞
⎜− ⎟
1 ⎜ 2⎟
h3 = b3 − b2 ⇒ h3 = ⎜ 1 ⎟
⎧< h3 , h1 >= 0 1 2
⎨ ⇒ β = − ,γ = 0 ⎜− 1 ⎟
⎜ 2⎟
⎩< h3 , h2 >= 0 2 , ⎝ ⎠
H = { h1 , h2 , h3 } este ortogonală .
hi
gi =
Considerăm baza G = { g1 , g2 , g3 } , || hi || , i =1 , 2 , 3 ⇒ || gi || = 1

⎫
⎪
⎛ 1⎞ ⎪
1 1 ⎜ ⎟ ⎪
g1 = h1 = ⎜ 1⎟
3 3⎜ ⎟ ⎪
⎝ 1⎠ ⎪
⎪
⎛ 1 ⎞⎪
1 1 ⎜ ⎟⎪
g2 = h2 = ⎜ 0 ⎟⎬
2 2 ⎜ ⎟⎪
⎝ − 1⎠ ⎪
|| h1 ||= < h1 , h1 > = 3 ⎛ 1 ⎞⎪
⎜− ⎟⎪
|| h2 ||= < h2 , h2 > = 2 2 2 ⎜ 2 ⎟⎪
g3 = h3 = 1
3 3⎜ 1 ⎟⎪
3 ⎜− ⎟⎪
|| h3 ||= < h3 , h3 > = ⎜ 2 ⎟⎪
2 ⇒ ⎝ ⎠⎭ ⇒
⇒ G este o bază ortonormală
V ( x ) = 2α 12 + α 22 + α 32
1 1
2 2 , xG = ( α1 , α2 , α3 ) T .

CAPITOLUL 7
PRINCIPIUL CONTRACŢIEI
7.1. Principiul contracţiei
Fie ( X,d ) un spaţiu metric . Fie ( x n ) n∈N * .
DEFINIŢIA 7.1.1.
Şirul ( xn ) este convergent în metrică dacă oricare ar fi ε > 0 , există N( ε ) astfel încât
oricare ar fi n ≥ N( ε ) , d( xn , x0 ) < ε .
DEFINIŢIA 7.1.2.
Şirul ( x n ) n∈N * este şir Cauchy în metrică dacă oricare ar fi ε > 0 , există N( ε ) astfel
încât oricare ar fi n ≥ N( ε ) , oricare ar fi p ∈ N* , d( xn+p , xn ) < ε .
Caz particular : X = R ⇒ d( x , y ) = || x – y || = | x – y |
DEFINIŢIA 7.1.3.
Spaţiul metric ( X,d ) se numeşte spaţiu metric complet dacă orice şir Cauchy este
convergent .
OBSERVAŢIE : Rn este un spaţiu metric complet .
Un şir de puncte din Rn este convergent dacă şi numai dacă în şirul componentelor sale,
fiecare componentă este convergentă către componenta corespunzătoare a limitei .
DEFINIŢIA 7.1.4.
Fie ( X,d ) un spaţiu metric .

O aplicaţie T : X → X se numeşte contracţie dacă există un număr real λ ∈ [0,1) astfel
încât d( T( x ) , T( y ) ) ≤ λ d( x , y ) , oricare ar fi x , y ∈ X .
DEFINIŢIA 7.1.5.
λ ∈ [0,1) se numeşte coeficient de contracţie .
EXEMPLUL 1 :

X = R , d( x , y ) = | x – y |
T( x ) = λ x , λ ∈ [0,1)
d( T( x ) , T( y ) ) = d( λ x , λ y ) = | λ x – λ y | = λ | x – y | = λ d ( x , y )
TEOREMA 7.1.1. ( Principiul contracţiei )
Fie ( X , d ) un spaţiu metric complet . Atunci pentru orice contracţie de

forma : T : X → X , există un punct u ∈ X astfel încât T( u ) = u şi acest punct este unic .
DEMONSTRAŢIE :
¾ existenţa :
Fie x0 ∈ X . Definim xn = T( xn-1 ) , n = 1 , 2 , (x n )n∈N , r = d( x0 , x1 ) .
d( x1 , x2 ) = d( T( x0 ) , T( x1 ) ) ≤ λ d( x0 , x1 ) = λ r ⇒ d( x1 , x2 ) ≤ λ r
d( x2 , x3 ) = d( T( x1 ) , T( x2 ) ) ≤ λ d( x1 , x2 ) = λ2 r ⇒ d( x2 , x3 ) ≤ λ2 r
………………………………………………………………………………………………
d( xn , xn+1 ) = d( T( xn-1 ) , T( xn ) ) ≤ λ d( xn-1 , xn ) = λn r ⇒ d( xn , xn+1 ) ≤ λn r
Oricare ar fi n ∈ N , oricare ar fi p ∈ N* obţinem relaţia :
d( xn , xn+p ) ≤ d( xn , xn+1 ) + d( xn+1 , xn+2 ) + … + d( xn+p-1 , xn+p ) ≤
≤ λn r + λn+1 r + … + λn+p-1 r = λn r ( 1 + λ + … + λp ) =
1 − λp λn r
λn r < p
= 1 − λ 1 − λ ( pentru că 1 – λ < 1 )
λn r
d (x n , x n + p ) ≤
Rezultă astfel că 1− λ .
1. r = 0 ⇒ d( x0 , x1 ) = 0 ⇒ x0 = x1 ⇒ T( x0 ) = x1 = x0 ⇒ u = x0 .
2. r > 0
λ ∈ [0,1) ⇒ nlim n
→∞ λ = 0 ⇒ oricare ar fi ε > 0 , există N( ε ) astfel încât n ≥ N( ε )
ε (1 − λ ) ε (1 − λ )
| λn − 0 |< ⇒ λn <
⇒ r r .
λn r ε (1 − λ )r
d (x n , x n + p ) ≤ ≤ =ε ⇒
1 − λ r (1 − λ ) xn este şir Cauchy .
Întrucât ( X,d ) este un spaţiu metric complet, rezultă că şirul (x n )n∈N este
convergent .
lim x = u lim
Notăm n →∞ n ⇒ n→∞ d( xn , u ) = 0 .

0 ≤ d( T( x ) , T( u ) ) ≤ λ d ( xn , u )
Dacă trecem la limită relaţia de mai sus , când n → ∞ , vom obţine :

lim
n →∞ d( T( x ) , T( u ) ) = 0 ⇒ T( u ) = u .
¾ unicitatea :
⎧T (u ) = u
⎨
Presupunem că există u , v ∈ X , u ≠ v , astfel încât ⎩T (v ) = v .
⎧d (u, v ) ≤ 0
d (u, v )(1λ2−31) ≥ 0 ⇒ ⎨
d( u , v ) = d( T( u ) , T( v ) ) ≤ λ d( u , v ) ⇒ <0 ⎩d (u, v ) ≥ 0
Deci d( u , v ) = 0 ⇒ u = v , ceea ce reprezintă o contradicţie . Aceasta înseamnă că punctul
fix este unic .
DEFINIŢIA 7.1.6.
Punctul u ∈ X este un punct fix al contracţiei T : X → X dacă T( u ) = u .
Cu această definiţie , principiul contracţiei se mai poate enunţa astfel :
Într – un spaţiu metric complet , ( X, d ) , pentru T : X → X , ecuaţia T( u ) = u are o

singură soluţie .
7.2. Metoda aproximaţiilor succesive
Metoda aproximaţiilor succesive reprezintă o metodă de rezolvare a ecuaţiilor şi a

sistemelor de ecuaţii prin alegerea convenabilă a unei contracţii .
Fie x0 o aproximaţie iniţială a soluţiei ecuaţiei f( x ) = 0 .

Determinăm T : R → R , considerăm şirul xn = T( xn-1 ) , n = 1 , 2 , … şi determinăm
coeficientul de contracţie .
Pentru a obţine o precizie dinainte cerută a rădăcinii ecuaţiei f( x ) = 0 , precizia fiind
ε , vom determina cel mai mic număr natural n ∈ N pentru care :
d ( x 0 , x1 ) d ( x 0 , x1 ) n
<ε d (x n , u ) < λ
1− λ 1− λ
EXEMPLUL 1 :
Să se determine rădăcinile ecuaţiei x3 + 12 x – 1 = 0 în intrevalul [0 , 1] cu patru

zecimale exacte .
Cu şirul lui Rolle arătăm că în intervalul [0 ,1] avem o rădăcină şi numai una
( R , d ) este un spaţiu metric complet , d( x , y ) = | x – y | .

1
x3 x2
+ 12 x – 1 = 0 ⇔ x ( + 12 ) = 1 ⇔ x = x + 12 2
T (x ) = 2
1
Fie T : R → R , x + 12 - vom arăta că este o contracţie .
2x 2x
λ = sup T ' ( x ) = sup −
2 2
= sup = = ∈ [0,1)
(x 2
+ 12 )
2
(x 2
+ 12 )
2
13 2
169
x0 = 0
1
x1 = T( x0 ) = T( 0 ) = 12
1
r = d( x0 , x1 ) = | x0 - x1 | = 12
Pentru a obţine rădăcina cu patru zecimale exacte ne oprim după n paşi ( n iteraţii ) ,
unde n este cel mai mic număr natural pentru care :
d ( x 0 , x1 ) n
n
1 169 ⎛ 2 ⎞ 1
λ < 0,0001 ⇒ ⋅ ⋅⎜ ⎟ <
1− λ 12 167 ⎝ 169 ⎠ 10000
Relaţia este adevărată pentru n = 2 .
u = x 2 = T ( x1 ) =
1 1 144
= = ≈ 0,0832
x + 12 ⎛ 1 ⎞
2 2
1729
⎜ ⎟ + 12
1
⎝ 12 ⎠ .

Radu Serban Algebra

Încărcat de

Informații document

Drepturi de autor

Formate disponibile

Partajați acest document

Partajați sau inserați document

Opțiuni de partajare

Vi se pare util acest document?

Este necorespunzător acest conținut?

Drepturi de autor:

Formate disponibile

Radu Serban Algebra

Încărcat de

Drepturi de autor:

Formate disponibile

Capitolul 1 Page 1 of 18

1.1. Noţiunea de spaţiu vectorial

Mulţimea nevidă V peste care s-au introdus două operaţii :

¾ 1) 1 ⊗ x = x , oricare ar fi elementul x din V

Fie V = Rn spaţiul real n dimensional , iar K = R

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

¾ 1) asociativitatea rezultă din asociativitatea numerelor reale

⎛ αx1 ⎞ ⎛ βx1 ⎞ ⎛ αx1 + βx1 ⎞

Elementele unui spaţiu vectorial le vom numi vectori.

Elementele corpului K le vom numi scalari.

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

Fie Pn [x] mulţinea tuturor polinoamelor de gradul n cu coeficienţi reali.

Fie (V,K) un spaţiu vectorial. Atunci elementul neutru θ este unic.

Din propoziţie ştim că există elementul neutru θ, oricare ar fi vectorul x din

θ1+x = x+θ1 = x pentru orice x aparţinând mulţimii V.

pentru x = θ2, θ1+θ2 = θ2+θ1 = θ2

1.2. Vectori liniar independenţi şi liniar dependenţi; bază şi dimensiune

Fie (V,K) un spaţiu vectorial.

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

se numeşte combinaţie liniară a vectorilor x1 , x2 , …, xn cu scalari din K.

Fie ( R3 , R ) un spaţiu vectorial , fie x1 , x2 , x3 vectori din acest spaţiu

1* Presupunem că x1 , x2 , … , xk-1 , xk , xk+1 , …, xn sunt liniar dependenţi şi vom

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

Presupunem că λ k este diferit de zero. Atunci:

2* Presupunem că cel puţin un vector este o combinaţie liniară a celorlalţi vectori şi

xk = α1 x1 + α2 x2 + … + αk-1 xk-1 + αk xk + αk+1 xk+1 + … + αn xn

α1 x1 + α2 x2 + … + αk-1 xk-1 + (-1) xk + αk+1 xk+1 + … + αn xn = θ

Vectorii x1 , x2 , … , xn care aparţin mulţimii V formează un sistem de generatori ai

Altfel spus, x1 , x2, …, xn formează un sistem de generatori dacă oricare ar fi

Fie (V,K) un spaţiu vectorial. Vectorii x1 , x2 , … , xn formează o bază a spaţiului V dacă

Fie ( R3 , R ) un spaţiu vectorial , fie x1 , x2 , x3 vectori din acest spaţiu

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

liniar, neomogen. Vectorii x1 , x2 , x3 formează un sistem de generatori deoarece sistemul de

Dimensiunea spaţiului vectorial V este egală cu numărul vectorilor unei baze.

Fie V un spaţiu vectorial peste corpul K , dimensiunea spaţiului V fiind n.

Din ipoteză ştim că B = { x1 , x2 , … , xn } este o bază. Aceasta înseamnă că vectorii x1 ,

Presupunem că x se scrie şi sub forma: x = β1x1 + β2x2 + … + βnxn (2)

x + (-x) = ( α1 – β1) x1 + ( α2 – β2 ) x2 + … + ( αn – βn) xn = θ

α1 – β1 = 0, α2 – β2 = 0, … , αn – βn = 0 , adică α1= β1, α2 = β2, … , α3 = β3.

V este un spaţiu vectorial de dimensiune n , iar B = { x1, x2, … , xn } este o bază în V.

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

Scalarii α1 , α2 , … , αn se numesc coordonatele vectorului x în baza B.

Din aceste două relaţii obţinem un sistem compatibil determinat:

(ii) Vectorii sunt liniar independenţi : θ = 0 + 0x + 0x2

1.3. Schimbarea coordonatelor unui vector la schimbarea bazelor

Fie (V,K) un spaţiu vectorial de dimensiune n.

Deoarece E şi G formează baze în spaţiul V, înseamnă că vectorii ei şi gi aparţin spaţiului V

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

g1 aparţine lui V, atunci g1 = c11 e1 + c12 e2 + … + c1n en

Matricea CEG = (cij ) se numeşte matricea de trecere de la baza E la baza G.

OBSERVAŢIE : Determinantul matricei CEG este diferit de zero, ceea ce înseamnă că

Fie (V,K ) un spaţiu vectorial de dimensiune n .

gi = ci1 e1 + ci2 e2 + … + cin en =

Acest sistem, scris matriceal, are forma : CT EG XG = XE ( 2’ )

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

1.4. Lema substituţiei

Fie (V,K) un spaţiu vectorial de dimensiune n .

Lema substituţiei răspunde la următoarele întrebări:

1) În ce condiţii mulţimea E* = { e1 , e2 , … , ei-1 , u , ei+1 , … , en } formează o bază în

Vom demonstra că mulţimea E* = { e1 , e2 , … , ei-1 , u , ei+1 , … , en } formează o bază şi că

1) Trebuie să arătăm că vectorii { e1 , e2 , … , ei-1 , u , ei+1 , … , en } sunt liniar independenţi .

file://E:\Personale\20042005\Cursuri\Algebra\DeCitit\parcurse\Algebra [curs] - Radu ... 23.10.2004

2) Trebuie să arătăm că { e1, e2, … , ei-1, u , ei+1, … , en } formează un sistem de generatori.

xE = λ*1 e1 + λ*2 e2 + … + λ*i-1 ei-1 + λ*i u + λ*i+1 ei+1 + … + λ*n en

xE = λ1 e1 + λ2 e2 + … + λi-1 ei-1 + λi u + λi+1 ei+1 + … + λn en