Apuntes Docentes PDF

1
APUNTES DOCENTES DE CÁLCULO INTEGRAL
YASMITH BOCANEGRA ARAGON
MARISEL ARDILA AMADOR
DEPARTAMENTO DE CIENCIAS BÁSICAS

UNIDADES TECNOLÓGICAS DE SANTANDER
APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

2
TABLA DE CONTENIDO
INTRODUCCIÓN................................................................................................................................ 4
1 LA INTEGRAL……………………………. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.1 Anti derivada o primitiva. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ………. 5
1.2 Integral Indefinida……………... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3 Área de una región en el plano. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.4 Sumatoria . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ... . . . . . 9
1.4.1 Propiedades de la Sumatoria. . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . ..9
1.5 Partición de un intervalo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.6 Suma de Riemann. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .... 10
1.7 Integral Definida. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.8 Área e integral definida. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
1.8.1 Propiedades de la integral definida. . . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . . . . . .10
1.8.2 Primer teorema Fundamental del Cálculo. . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . .15
1.8.3 Segundo teorema Fundamental del Cálculo... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.8.4 Teorema del valor Medio. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 16
1.9 Valor Promedio. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2. TÉCNICAS DE INTEGRACIÓN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19
2.1 Regla de la Sustitución Simple. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19
2.2 Integración por Partes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . .20
2.3 Integración de Funciones Trigonométricas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.4 Sustitución Trigonométrica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5 Integración por Fracciones Parciales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3. APLICACIONES DE LA INTEGRAL. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

3
3.1 Área entre Curvas: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.2 Volúmenes de Sólidos de Revolución. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 32
3.2.1 Método de Discos y Arandelas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.2.2 Método de Cascarones Cilíndricos. . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . .. ... 34
3.2.3 Volumen por Secciones Transversales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . .35
4. COORDENADAS POLARES. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
4.1 Sistema de Coordenadas s Polares. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .38
4.2 Representación de Puntos en el Plano Polar. . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 38
4.3 Coordenadas Polares y Cartesianas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.4 Ecuaciones Polares... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 39
4.5 Área entre Curvas Polares. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
BIBLIOGRAFÍA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

4
INTRODUCCIÓN
Esta asignatura contribuye a desarrollar un pensamiento lógico, heurístico y algorítmico al modelar

fenómenos y resolver problemas en los que interviene la variación. Hay una diversidad de
problemas en la ingeniería que son modelados y resueltos a través de una integral, por lo que
resulta importante que el ingeniero domine el Cálculo integral.
Buscando la comprensión del significado de la integral se propone un tratamiento que comience

por lo concreto y pase luego a lo abstracto, así se sugiere que la integral definida se estudie antes
de la indefinida puesto que aquélla puede ser abordada a partir del acto concreto de medir áreas.
Se incluye la notación sumatoria para que el alumno la conozca y la maneje en la representación
de sumas de Riemann. La función primitiva se define junto con el Teorema Fundamental por estar
íntimamente ligados. Las integrales impropias se ubican en esta unidad por ser un caso de integral
definida, para aprovechar el contexto. Una vez que se abordó la construcción conceptual de la
integral definida, se estudian la integral indefinida y los métodos de integración, para tener más
herramientas en la construcción de la anti derivada, necesaria para aplicar el Teorema
Fundamental.
Las aplicaciones incluidas en el temario son las básicas, adecuadas a las competencias previas de
los estudiantes, con el objetivo que sean ellos quienes planteen por sí mismos la integral a aplicar y
resolver. Se complementa el tratamiento de aplicaciones con la identificación, por parte del alumno,
de la integral en diferentes temas de ingeniería. Por último se incluye el estudio del sistema de
coordenadas polares para que de esta manera extrapole los concepto trabajados en las
coordenadas cartesianas a otro sistema de representación de magnitudes y funciones. Como es el
sistema polar.

5
UNIDAD 1 LA INTEGRAL
Definición 1.1 Anti derivada o primitiva
Se dice que la función F es una anti derivada o primitiva de f , en un intervalo I si y solo si

F ( x)  f ( x) para todo x en I
Ejemplo 1.1
Si se quiere encontrar una función F cuya derivada sea f ( x)  3x 2 . Por lo que se sabe de
derivadas es posible afirmar que
d 3
F ( x)  x3 Porque  x   3x 2
dx  
Teorema 1.1.1
Si F es una anti derivada de f en un intervalo I, entonces G es una anti derivada de f en el intervalo

I si y sólo si G es de la forma G(x)= F(x) +C, para toda x en I, donde es una constante.
A continuación se presentan las antiderivadas de algunas funciones:
Función : f  x  Antiderivada : F  x 
xn x n 1
C
n 1
senx  cos x  C
cos x s enx  C
s ec 2 x tan x  C
csc2 x  cot x  C
sec x tan x sec x  C
csc xcotx  csc x  C
1 sen1 x  C
1  x2
1 tan 1 x  C
1  x2
1 sec1 x  C
x x2 1
x x
C
x x
a a
C
ln a
1 ln x  C
x

6
Definición 1.2 Integral Indefinida
La integral indefinida de la función f con respecto a x es igual a la anti derivad de f.
Ejemplo1.2
Escribamos la integral definida de las funciones reales básicas.

7
Ejemplo 1.3
Halle las siguientes integrales indefinidas:
Los antiguos griegos dieron una regla para calcular la medida del área de un rectángulo (producto
de la base por la altura), de aquí se deduce que el área de un triángulo rectángulo es igual a "un
medio del producto de los catetos". Debido a que un polígono se puede descomponer en
triángulos, la obtención de su área se consigue mediante la suma de las áreas de los triángulos en
que se ha dividido. Este procedimiento de medir áreas sólo es aplicable a figuras planas limitadas
por segmentos de rectas.
Para medir el área de una figura limitada por curvas se debe recurrir a otro método, que es el que
vamos a estudiar a continuación.
Definición 1.3 Área de una región en el plano
Entonces si y  f (x) es una función positiva y se quiere encontrar el área bajo la curva desde
x  a hasta x  b ,tomando f ( xi ) el mayor valor que toma la función f (x) en el intervalo
xi1 , xi  y f ( xi1 ) el menor valor de la función en el intervalo (si la función f es creciente
en
a, b ), haciendo una partición regular del intervalo a, b donde x  (b  a) / n , si f (ci ) es
el valor de f en el i  ésimo subintervalo. La medida de la región R está dada por:
n
A  lim
n
 f (c )x .
i 1
i
Un método de aproximación al área que se está buscando es, haciendo una subdivisión del
 
intervalo a, b en subintervalos de longitudes iguales x  (b  a) / n (a lo que se le llamará
partición regular del intervalo). La Partición de un intervalo a, b es un conjunto finito de
puntos de a, b de los cuales uno es a y otro es b . Donde: x0  a, x1  a  x,...,

8
xi  a  ix,..., xn1  a  (n  1)x, xn  b . Asimismo, se denota el i-ésimo intervalo por

xi1 , xi , siendo n  N es una manera de numerar los puntos de la partición; n es el número de
partes.
Figura 2
Puesto que f es continua el teorema del valor extremo garantiza la existencia de unos valores
mínimo y máximo de f (x) en cada subintervalo:
f mi   valor mínimo de f (x) en el i-ésimo intervalo

f M i   valor mínimo de f (x) en el i-ésimo intervalo
Por tanto, podemos definir un rectángulo inscrito y un rectángulo circunscrito como se muestra
en la figuras 3 y 4
Figura 3 Figura 4
La relación entre las áreas de estos dos rectángulos es la siguiente:
(Área del rectángulo inscrito) = f mi  x  f M i  x = (área del rectángulo circunscrito)
Sumando estas dos áreas, tenemos
n n
Suma inferior = s n   f (m )x
i 1
i Suma superior = S n   f (M )x ;
i 1
i donde sn  S n
De hecho, si tomamos el límite cuando n   , ambas sumas superior e inferior existen y son
iguales. De este modo, la elección de x en el intervalo i-ésimo no afecta el valor del límite, por lo
que podemos elegir libremente un valor y lo definiremos como ci . Esto es

9
n n n
lim  f (mi )x  lim  ( M i )x  lim  f (ci )x
n n n
i 1 i 1 i 1
Definición 1.4 Sumatoria

n
(a , a , a ,...,a n ) , el símbolo a n
Dado un conjunto de números i i 1 i 2 k i representa su suma indicada
n
a
k i
n  ai  ai 1  ai  2  ...  an

o sumatoria. Esto es . La letra griega sigma mayúscula, ,
a
denota la sumatoria, k representa el k-ésimo término, la letra k se llama índice de sumatoria y
adquiere valores enteros sucesivos, los números i y n son los valores extremos del índice de
sumatoria.
Teorema 1.4.1 Propiedades de la Sumatoria:
n n n
1.  c  cn; c: constante
k 1
2. c  a
k 1
k c ak ; c: constante
k 1
n n n b bc
3. a
k 1
k  bk    ak   bk
k 1 k 1
4.  F (k )   F (k  c)
k a k a c
b b c n
5.  F ( k )   F (k  c)
k a k  a c
6. F (k )  F (k  1)  F (n)  F (0)
k 1

7.1 Si n   entonces 7.2
n
n(n  1)(2n  1)
n(n  1) k
n


2
k 6
2 k 1
k 1
7.3 7.4
n
n (n  1) 2 2 n
n(n  1)(6n 3  9n 2  n  1)

k 1
k  3
4

k 1
k  4
30
Definición 1.5 Partición de un Intervalo cerrado:

 
Una partición  de un intervalo cerrado a, b es el conjunto de todos los subintervalos de la forma
x0 , x1 , x1 , x2 , x2 , x3 ,
..., xn1 , xn , y a  x0  x1  x2  x3  ...  xn1  xn  b, n  .
La longitud del i  ésimo subintervalo xi 1 , xi , xi , está dada por xi  xi  xi 1 . La longitud
del subintervalo más largo de la partición  se llama norma de la partición y se denota por  .
En la figura 4 se ilustra una partición cualquiera de a, b .

10
Definición 1.6 Suma de Riemann:
 
Sea f una función definida en a, b , y sea  una partición cualquiera de a, b , una suma de  
Riemann (llamada así en memoria del matemático alemán G.F. Bernard Riemann (1826- 1886)) es
la que está dada por:
 f ( ) x  f ( ) x  f (
i 1
i i 1 1 2 ) 2 x  f ( 3 ) 3 x  ...  f ( i ) 4 x  ...  f ( n ) n x
Donde  i es un punto cualquiera del i  ésimo subintervalo y,  i x es la longitud de este

i  ésimo subintervalo.
Definición 1.7 la Integral definida:
 
Sea f una función definida en a, b , la integral definida de f entre a y b , denota como
n n
f ( x)dx  lim  f ( i ) i x  lim  f ( i ) i x.
b

b
a
f ( x)dx, está dada por: a
x 0 i 1 n i 1
b
En 
a
f ( x)dx, las denominaciones son:  : signo de integración ( es una “s” estirada); a:
extremo inferior; b : extremo superior; f (x) integrando.
Definición 1.8 Área e Integral definida:
Si f es continua en a, b , y f ( x)  0 x  a, b , entonces el Área A de la Región R bajo la

b
gráfica de f entre a y b , está dada por: A   f ( x)dx
a
Teorema 1.8.1 Propiedades de la Integral Definida:
Para facilitar el cálculo de una integral definida, sin tener que recurrir a la definición dada en
función de la sumatoria, se proporcionan las siguientes propiedades fundamentales:
b a a
1. si a  b, entonces: 
a
f ( x)dx   f ( x)dx
b
2. si f (a) existe, entonces: a
f ( x)dx  0
3. Si k es una constante cualquiera, entonces 4. Si f es integrable en a, b y,   k es una

b
 kdx  k (b  a)
constante arbitraria, entonces:
b b
 k  f ( x)dx  k 
a
f ( x)dx
a a
5. Si f y g son integrables en a, b , entonces 6. Si f es integrable en a,b, a, c y c, b , y

f  g también es integrable en a, b y: a  c  b , entonces:
b c b
a  f ( x)  g ( x)dx  a f ( x)dx  a g ( x)dx  f ( x)dx   f ( x)dx   f ( x)dx

b b b
a a c
6. Si f es integrable en un Intervalo cerrado I y, 7. Si f es integrable en a, b y f ( x)  0

a, b, c I , entonces: x  a, b , entonces:
b

a
f ( x)dx  0

11
b c b

a
f ( x)dx   f ( x)dx   f ( x)dx
a c
8. Si f y g son integrables en a, b y 9. Sea f continua en a, b . Si m es el valor

f ( x)  g ( x) x  a, b , entonces mínimo absoluto y M el valor máximo absoluto de
b b  
f en a, b , y m  f ( x)  M , a  x  b

a
f ( x)dx   g ( x)dx
a entonces,
b
m(b  a)   f ( x)dx  M (b  a)
a
La interpretación geométrica es: Como
f ( x)  0 x   
a,b , el área de la región
bajo la curva de f (x) , encerrada entre las
rectas x  a y x  b y el eje x , está dada
b
por la integral a
f ( x)dx . El área de la región
rectangular de dimensiones M y (b-a) es
mayor que el área dada por la integral, y el
área de la región rectangular de dimensiones
m y (b-a) es menor que el área dada de la
integral.
Ejemplo 1.4
Determine la suma por medio de la definición y propiedades de la sumatoria:

2 20
k
k 3
k  2
 3k (k
k 1
2
 2) =
2 1 0 1 2 3 20 20 20
     
 2  3 1  3 0  3 1  3 2  3 3  3  (3k 3  6k )  3 k 3  6 k
k 1 k 1 k 1
2 2
20 (21) 20(21)
 2 1 0 1 2 3 1 1 2 13   6
       2   0    4 2
1 2 3 4 5 6 2 4 5 2
3  400  441
  3  20  21
 40  10  5  8  10  50  23 27 4
  = 
 132300  1260 = 133560
20 20 20
Ejemplo 1.5
Evalúe el área de la región dada, emplee rectángulos inscritos o circunscritos según se indique.
Para cada ejercicio trace una figura que muestre la región y el i-ésimo rectángulo.
a. La región acotada por la curva de y  x 2 , el eje x , y la recta x  2 , rectángulos inscritos,
(figura a). Dividimos 0,2 en n subintervalos, cada uno de longitud x : x0  0, x1  x ,
20 2
x2  2x , ..., xi 1  (i  1)x , xi  ix , …, xn  2. x   ; f ( x)  x 2 . Como f
n n

12
es creciente en 0,2, el valor mínimo absoluto de f en el i-ésimo subintervalo ( xi 1 , xi ) es

n n
f ( xi 1 ) , Por lo tanto: A  lim  f ( xi 1 )x  lim  ((i  1)x) 2 x,
n n
i 1 i 1
figura b
figura a
b. La región acotada por y  2 x , el eje x , y las rectas x  1 y x  4; rectángulos circunscritos,

(Figura b)
 
Dividimos 1,4 en n subintervalos, cada uno de longitud x : x0  1, x1 1  x ,
x2  1  2x ,…,
4 1 3
xi  1  ix,..., xn  4 . x   , . Como f es creciente en 1,4 , el valor máximo
n n
absoluto de f en el i-ésimo subintervalo ( xi 1 , xi ) es f ( xi ). Por lo tanto:
n n
A  lim  f ( xi )x  lim  (1  ix)x,
n n
i 1 i 1
n n
 3 3 n
6 6 n n

A  lim  2(1  ix)x  lim  21  i     lim  2 (n  3i)  lim 2   n  3 i 
i 1  n  n n i 1 n  i 1 i 1 
n n n n
i 1
6  2 3n(n  1)  6  5n 2  3n   3  3
A  lim  n   n 2 
 lim   lim 3 5    3 lim  5    3(5  0)
n n 2
 2  n  2  n 
 n n 
 n
A  15 unidades cuadradas
Ejemplo 1.6
1
Halle la suma de Riemann para la función f ( x)  en el intervalo 1  x  3 , (Figura c); emplee
x
5 9 8
la partición dada  : x0  1, x1  , x2  , x3  , x4  3; y los valores de  i :
3 4 3

13
5 5 11
1  ,  2  2,  3  ,  4  . Trace la gráfica de la función en el intervalo dado, y muestre los
4 2 4
rectángulos cuyas medidas de área sean los términos de la suma de Riemann
4
 f   x  f ( ) x  f (
i 1
i i 1 1 2 ) 2 x  f ( 3 ) 3 x  f ( 4 ) 4 x
4
 5  5  9 5  5  8 9  11  8
 f   x  f  4  3 1  f (2) 4  3   f  2  3  4   f  4  3  3 
i 1
i i
4
4 2  1  7  2  5  4 1 8 7 1 4 1469
 f ( ) x  5  3   2  12   5  12   11  3   15  24  6  33 = 1320
i 1
i i
Figura c
Ejemplo 1.7
Encuentre el área exacta de la región acotada por la recta y  2 x  1 , el eje x y las rectas x  1 y
x  5 , como se indica: a) Exprese la medida del área como límite de una suma de Riemann con
particiones regulares; b) Exprese este límite con la notación de integral definida; c) Evalúe la
integral definida con el método de esta sección y una elección indicada de 1 . Trace una grafica
que muestre la región.
1,5 en
n
a) A  lim
n
 f ( ) x
i 1
1 i (1). Haciendo una partición regular de n subintervalos,
entonces:
5 1 4
 i x  x   (2). Sustituyendo (2) en (1)  A  lim
n
4
n n n
 f (1 ) 
n i 1
5
b) A   (2 x  1)dx
1
4
c) Si escogemos 1 como el punto extremo derecho de cada subintervalo, se tiene 1  1 
n
8
, 2  1 ,...,
n
4
 i  1  i,..,  n  5. Puesto que f ( x)  2 x  1 , entonces
n
 n  4i 
 1  n  4i   1;
2
f ( i )  2 
 n  n

14
n
2 4
  n n  4i 1 n
5
A   (2 x  1)dx  lim
1 n
i 1
4 2 n
 4 2  n n
 n 
 lim   n  4i   1  lim   n  4 i   1
i 1  n  n n  n  i 1 i 1 
n n
i 1 
 lim
4 2 2
   4

n  2n(n  1)  n  lim 2 6n 2  4n  n 2  

n n n
 n n
4
  4
 
 lim 2 5n 2  4n  4 lim 5    4 lim 5  lim 
4
n n n
 n  n   n  n
A   (2 x  1)dx  45  0  45  20 unidades cuadradas
5
Ejemplo 1.8
2
Encuentre el valor exacto de la integral definida 
0
x 2 dx por Sumas de Riemann.
Consideremos una partición regular del intervalo 0,2en n subintervalos. Entonces x  2 n . Si
escogemos 1 como el punto extremo derecho de cada subintervalo, se tiene:
2
2 2 2  2i  4i 2
1  ,  2  2 ,..., i  i ,..., n  2 . Como f ( x)  x 2 , entonces f ( i )     2
n n n n n

 4i 2  2 8  n(n  1)(2n  1) 
 
n
8 n 2 4
 
2
0     i  lim 3   lim 3 2n 3  3n 2  n
2
x dx lim   lim 
  n 3n
n 2 n n 3 n n
i 1  n  n i 1 6
 3 1  4 1 4
 lim 2   2   lim 2  lim  lim 2   2  0  0
4 3
3 n  n n  3 n n n n n
 3
2 8
  x 2 dx 
0 3
Nota: La interpretación geométrica del resultado es la siguiente: como x  0, x  0,2, la
2
región R, acotada por la curva y  x , el eje x y las rectas x  0 y x  2, tiene un área cuya
2
medida es de 8 3 unidades cuadradas.
Ejemplo 1.9
Aplique las propiedades de la integral definida para evaluar las siguientes integrales:
5 5 5 3 3
  4dx  4(5  2)  4(3)   4dx  12  4 x 2 dx =  4 x dx  0
2
1. 4dx = 2.
2 2 2 3 3
Ejemplo 1.10
Use las propiedades para resolver los siguientes ejercicios:

15
7 6
1.  3
2xdx 2. 
3
3  x dx
f es una función polinomial, por lo que es continua en f ( x)  3  x : 3  x  0  x  3  Dom   3, 
R , y en particular, continua en 3,7  f es continua en  3,  y particular en  3,6
f ' ( x)  2 : Siempre existe y nunca es 0; por lo que no 1
tiene números críticos. f ' ( x)  , f ' no existe en x  3 y f ' ( x) nunca
f (3)  2(3)  6 : Valor mínimo absoluto 2 3 x
es cero, entonces el único número critico de f es  3
f (7)  2(7)  14 : Valor máximo absoluto.
Por lo tanto de acuerdo con el teorema 10, se tiene: f (3)  0 : Valor máximo absoluto de f en  3,6
7
6(7  3)   2 xdx  14(7  3)  24   2 xdx  56 R
7
f (6)  3 : Valor mínimo absoluto de f en  3,6
3 3 De acuerdo con el teorema 10, se tiene:
espuesta: El valor de la integral está en el 24,56 0(6  3)  
6
3  x dx  3(6  3)  0  
6
3  x dx  27
3 3
Respuesta: El valor de la integral está en el 0,27

2
b) 2
( x 3  1)dx  4 . Solución:
2 2
2
( x 3  1)dx  f ( z )(2  (2))   ( x 3  1)dx  4 f ( z ) ,
2
2
 ( x  1)dx  4 , esto es 4 f ( z )  4, f ( z )  1 es
3
Pero
2
decir, z  1  1  z
3 3
 0;  z  0
De tal modo que :
2
 2
( x 3  1)dx  f (0)(2  (2))
Teorema 1.8.2 Primer Teorema Fundamental del Cálculo
Sea f continua en el intervalo cerrado [a,b], y sean x un punto en (a,b). Entonces,
Ejemplo 1.11
d x 1 1
Calcule la derivada: a) 
dx t  4
2 4
dt = 4
x 4
d x3 3 2 d x3 3 2 d x3 3 2 du
b)
dx 1
t  1dt Aplicamos la regla de la cadena:
dx 1
t  1dt 
du 1
t  1dt 
dx
. (1)
du d x3 3 2 d u 3 2
Si u  x ,   3x 2 , sustituyendo en (1) se obtiene:  t  1dt 
du 1
t  1dt  3x 2 ,
3
dx dx 1

16
d x3 3 2
dx 1
 t  1dt  3 u 2  1  3x 2  3 ( x 3 ) 2  1  3x 2  3 x 6  1  3x 2
d x3 3 2
dx 1
 t  1dt  3x 2 3 x 6  1
Teorema 1.8.3 Segundo Teorema Fundamental del Cálculo
Sea f continua en [a,b], y sea F cualquier anti derivada de f en [a,b],. Entonces
Ejemplo 1.12
Evalúe la siguiente integral
Teorema. 1.8.4 Teorema del valor Medio:

 
Si f es una función continua en a, b , entonces existe un número z en a, b , tal que:
b
a
f ( x)dx  f ( z )(b  a)
a, b ; en este caso, a f ( x)dx se toma como el área de la región encerrada

b
Sea f ( x)  0 , x 
por la curva de f (x) , las rectas x  a y x  b y el eje x . Entonces, existe un número

z  a, b tal que el área del rectángulo ABCD cuyas dimensiones son la altura f (z ) y el ancho
(b  a) es igual área de la región ABDF.
El número z no es necesariamente único, no obstante, el teorema 11, garantiza al menos la

existencia de un número que satisfaga la igualdad.

17
Definición1.9 El Valor Promedio
Sea f continua en a, b , el valor medio ( o promedio ), f med , de f en a, b es:

1 b
b  a a
f med  f ( x)dx
Ejemplo 1.13
2
Halle el valor promedio de f(x) = 3x - 2x en el intervalo [1, 4]. Calculamos:
4
1  3x 3 2 x 2 
b 4
1 1 1
f prom   f ( x)dx   (3x  2 x)dx      (64  16  1  1)  16
2
ba a 31 3 3 2 1 3
Ejemplo 1.14
En los siguientes ejercicios encuentre el valor de z que satisfaga el Teorema del valor medio para
2 2
la integral definida. Emplee los siguientes resultados: 
0
x 2 dx  8 3 , 
2
( x 3  1)dx  4

18
2
a)  0
x 2 dx . Solución:
2 2
0
x 2 dx  f ( z )(2  0)   x 2 dx  2 f ( z ) , Pero
0
2
 x dx  8 / 3,  2 f ( z )  8 / 3;  f ( z)  4 / 3,
2
0
Esto es z  4 / 3  z  2 3 / 3, como  2 3 / 3  0,2

2
 
se toma z  2 3 / 3 de tal modo que
2
0
x 2 dx  f (2 3 / 3)(2  0)

19
UNIDAD 2 TECNICAS DE INTEGRACIÓN
2.1 Regla de la sustitución simple o cambio de variable
Sea g una función derivable y supóngase que F es una anti derivada de f., entonces
 f ( g ( x)) g ( x)dx . La sustitución o cambio de variable u  g (x)

la transforma en  f (u)du = F(u) = F(g(x)) +C
Ejemplo 2.1
Aplique el método de la sustitución simple par a evaluar las siguientes integrales
1
a.  x 2 ( x 3  1)10 dx 
 ( x 3  1)10 3x 2 dx
3
u  x  1  du  3x dx
3 2
Entonces
1 10 u 11
 x ( x  1) dx  3  u du  33  C
2 3 10
1 3
x ( x 3  1)10 dx  ( x  1)11  C
2
33
sec 2 3 t 2  3dt 
b.
t
dt =
3  sec 2 3 t 
2 t


3
u  3 t  du  dt
2 t
Entonces
sec 2 3 t 2 2
 t
dt 
3  sec 2 udu  tan u  C
3
sec 2 3 t 2
 t
dt 
3
tan 3 t  c
d . sec xdx
sec x(sec x  tan x) sec 2 x  sec x tan x
 sec xdx   sec x  tan x
dx  
sec x  tan x
dx
u  sec x  tan x
du  (sec x tan x  sec 2 x)dx
du
 sec xdx   u  ln u  C
 sec xdx  ln sec x  tan x  c

20
2.2 Integración por partes
Sean u y v funciones derivables e integrables entonces aplicando la regla del producto para
derivar y posteriormente integrando a ambos lados obtenemos una fórmula para integral un
producto de funciones
d (u.v)  udv  vdu
 d (u.v)  udv   vdu

 udv  u.v   vdu
Ejemplos 2.2
Usando l integración por partes evalúe las siguientes integrales

a. xsenxdx
u  x  du  dx
dv  senxdx  v   cos x
Aplicando la regla de por partes se obtiene
 xsenxdx   x cos x   cos xdx

 xsenxdx   x cos x  senx  c
b. x 2 ln xdx
dx
u  ln x  du 
x
x3
dv  x 2 dx  v 
3
Aplicando la regla de por partes se obtiene
x3 1 2
 x ln xdx  3 ln x  3  x dx
2
1 3 1 3
 x ln xdx  3 x ln x  9 x  c
2
c. x sec x tan xdx

u  x  du  dx
dv  sec x tan xdx  v  sec x
 x sec x tan xdx  x sec x   sec xdx
 x sec x tan xdx  x sec x  ln sec x  tan x  c
d . cos x dx

21
Primero se realiza una sustitución simple
w  x  w2  x  2wdw  dx
El integrando quedaría
 cos xdx  2 w cos wdw

Aplicando integración por partes
u  w  du  dw
dv  cos wdw  v  senw
Aplicando la regla de integración por partes se obtiene:
 w cos wdw  wsenw   senwdw  wsenw  ( cos w  c ) 1
Y el resultado sería
 cos xdx  2(wsenw  ( cos w  c1 ))  2wsenw  2 cos w  c

w  x , entonces:
Reemplazando
 cos xdx  2 x sen x  2 cos x  c
2.3 Integración de funciones trigonométricas
En este apartado aprenderemos a integrar funciones que presentan potencias trigonométricas, es

decir, funciones con alguna de las siguientes formas:
m n
Caso: sen xcos x
-Si al menos uno de los exponentes es impar, se separa un término de la potencia impar se hace la
2 2
sustitución con la función que no se separó el factor y se utiliza la identidad sen x + cos x = 1.
Ejemplo 2.3
a. sen5 x cos 2 xdx   ( sen2 x)2 cos 2 xsenxdx   (1  cos 2 x)2 cos 2 xsenxdx 
  (1  2 cos 2 x  cos 4 x) cos 2 xsenxdx   cos 2 xsenxdx  2 cos 4 xsenxdx   cos 6 xsenxdx
u  cos x
du   senxdx
1 2 1
 u du  2 u du   u du   3 u u5  u7  C
2 4 6 3
5 7
1 2 1
 sen x cos xdx   3 cos x  5 cos x  7 cos x  c
5 2 3 5 7

22
- Si ambos exponentes son pares se usan las identidades trigonométricas:

2 2
Cos x = (1+cos2x)/2 y sen x =(1-cos2x)/2
Ejemplo 2.4
1 1 1
b. sen2 3x cos 2 3xdx   (1  cos 6 x)(1  cos 6 x)dx   (1  cos 2 6 x)dx   sen2 6 xdx
4 4 4
1 1 1
8  (1  cos 12 x)dx  x 
8 96
sen12 x  C
1 1
 sen 3x cos 3xdx  x sen12 x  c
2 2
8 96
m n
Caso: tan x sec x
2
- Si el exponente de secx es par, se separa un factor sec x , se hace u=tanx , se utiliza la identidad
2 2
1+tan x = sec x
Ejemplo 2.5
d . tan6 x sec4 xdx   tan6 x sec2 x sec2 xdx   tan6 x(1  tan 2 x) sec2 xdx
u  tan x
du  sec2 xdx
u7 u9
 u (1  u )du   u du   u du   C
6 2 6 8
7 9
1 1
 tan x sec 4 xdx  tan 9 x  tan 7 x  c
6
9 7
- Si el exponente de tanx es impar, se separa el factor sec x tanx y se hace u= secx.
2.4 Sustitución trigonométrica
A menudo es posible hallar la antiderivada de una función cuando el integrando presenta

expresiones de la forma:
a 2  u 2 ; a 2  u 2 ; u 2  a 2 . Siendo a una constante y u una función de x
Se elimina el radical haciendo la sustitución trigonométrica pertinente; el resultado es un integrando
que contiene funciones trigonométricas cuya integración nos es familiar.
Completa la siguiente tabla:
Expresión en el integrando Sustitución trigonométrica Radical se convierte

a2  u 2 u  asen a cos 
a2  u 2 u  a tan a sec
u2  a2 u  a sec a tan 

23
Ejemplo 2.6
Usando una sustitución trigonométrica evalúe la integral
dx
a.
x2 4  x2
Solución
En este ejercicio la expresión dentro del radical es de la forma a 2  u 2 ; por lo que la sustitución
debe ser:
x  2sen
dx  2 cos d
dx 2 cos  1 1
x 2
4  x2

4sen  2 cos 
2
d   csc2 d   cot   C
4 4
dx 4  x2
x 2
4  x2

4x
c
1
b. dz
( z 2 z  5)
2
2
Solución
1 dz
 ( z 2 z  5)
2 2 dz  
(( z  1) 2  4) 2
z  1  2 tan
dz  2 sec2 d
1 2 sec2  1 1 1 1
 ( z 2 z  5)
2 2 dz  
16 sec 
4
d   cos 2d   (1  cos 2 )d   
8 16 16 32
sen2  C
1 1 1
 ( z 2 z  5)
2 2 dz 
16
  sen cos   C
16
1 1 z 1 1 z 1
 ( z 2 z  5)
2 2 dz   tan 1
8 ( z 2 z  5) 16
2
2
C
1 1 z 1 1 z 1
 ( z 2 z  5)
2 2 dz   tan1
8 ( z 2 z  5) 16
2
2
c

24
sen2 x
c. dx
sen 4 x  9
Solución: Primero debe realizarse una sustitución simple de la siguiente forma
u  sen 2 x du  2senx cos xdx  du  sen2xdx
du
Por lo que la integral se transforma a  u2  9
Sea u  3sec  du  3sec tand
Con estos datos construye el triangulo______________________
u 2  9  3 tan x
2 2 4
du 3 sec  tan d u u 9 sen x sen x  9
    sec d  ln sec   tan   c  ln   c  ln  c
2
u 9 3 tan  3 3 3 3
2.5 Integración por fracciones parciales
Veremos cómo integrar cualquier función racional expresándola como una suma de fracciones
P( x)
más simple. Una función racional tiene la forma general donde P(x) y Q(x) son polinomios.
Q( x)
Las funciones racionales se clasifican en:
Impropias: Cuando el grado de P es mayor que el grado de Q, entonces se realiza la división entre
P y Q hasta obtener un cociente C y un residuo R tal que el grado de R es menor que el grado de
Q
P( x) R
C donde R y Q son polinomios
Q( x) Q( x)
Propias: Cuando el grado se P es menor que el grado de Q, entonces puede descomponerse en

una suma de fracciones simples siempre que Q sea factorizable (factores lineales y cuadráticos)
de las siguientes cuatro formas:
Factores lineales distintos
P( x) A B
  Donde a, b, A y B son constantes
( x  a)( x  b) ( x  a) ( x  b)
Factores lineales repetidos

P( x) A B C
   ...  Donde n es un entero positivo y a, A, B y C son
( x  a) n
( x  a) ( x  a) 2
( x  a) n
constantes

25
Factores cuadráticos distintos

P( x) Ax  B Cx  D
  donde a, b, c y d, A, B, C y D son constantes
(ax  b)(cx  d ) (ax  b) (cx 2  d )
2 2 2
Factores cuadráticos repetidos

P( x) Ax  B Cx  D Ex  F
   ....  Donde n es un entero
(ax  b)
2 n
(ax  b) (ax  b)
2 2 2
(ax 2  b) n
positivo y a, b, A, B, C, D, E y F son constantes
Ten en cuenta que existe la combinación de las formas anteriores
Ejemplo 2.7
Evalúe las siguientes integrales
1
a. dx
9x  x 2
4
Es una función racional propia entonces el primer paso es factorizar el denominador y separar en
fracciones parciales así:
1 A B Cx  D
 2   2
x (9 x  1) x
2 2
x 9x  1
Los coeficientes A, B, C y D se pueden encontrar de la siguiente manera:
 Se multiplica cada término de la identidad por el mínimo común divisor

1  A(9 x 2  1)  Bx(9 x 2  1)  (Cx  D) x 2
 Se destruyen los paréntesis

1  9 Ax 2  A  9Bx 3  Bx  Cx 3  Dx 2
 Se agrupan términos semejantes

1  (9B  C ) x 3  (9 A  D) x 2  Bx  A
 Se encuentran las ecuaciones para determinar coeficiente
9B  C  0
9A  D  0
B0
A 1
 Se resuelve el sistema y se obtiene

1 1 0 0x  9 1 9
 2   2  2  2
x (9 x  1) x
2 2
x 9x  1 x 9x  1
De tal manera que:

26
1  1 9 
 9x 4
x 2
dx    2  2
x
dx
9x  1 
 Se integra y se obtiene
1 1
 9x 4
x 2
dx    3 tan 1 3x  c
x
x2
b. 2 dx
x  x6
Es una función racional impropia por lo que se realiza la división de polinomios y se reescribe de la
forma: parte entera y fracción propia.
x2 x6
 1 2
x  x6
2
x  x6
Para integrar la fracción propia se procede como en el ejemplo anterior
 Se Factoriza el denominador y se separar en fracciones parciales

x6 A B
 
( x  3)( x  2) ( x  3) ( x  2)
Los coeficientes A y B se pueden encontrar de la siguiente manera:
 Se multiplica cada término de la identidad por el mínimo común divisor

x  6  A( x  2)  B( x  3)
 Se destruyen los paréntesis

x  6  Ax  2 A  Bx  3B)
 Se agrupan términos semejantes

x  6  ( A  B) x  (3B  2 A)
 Se encuentran las ecuaciones para determinar coeficiente
A B 1
3B  2 A  6
 Se resuelve el sistema y se obtiene

x6 9 4
 
( x  3)( x  2) 5( x  3) 5( x  2)
De tal manera que:
x2 9 dx 4 dx
 x 2  x  6 dx   dx  5  ( x  3)  5  ( x  2)
 Se integra y se obtiene
2
x 9 4
x 2
 x6
dx  x  ln( x  3)  ln( x  2)  C
5 5

27
UNIDAD 3 APLICACIÓN DE LA INTEGRAL
3.1 Área entre curvas
Si f y g son continuas en a, b y g (x)  f (x) para todo x en a, b , entonces el

área de la región limitada por las gráficas de f y g y las líneas verticales x  a y x  b es
A  a  f ( x)  g ( x) dx
b
Es importante tener en cuenta que el desarrollo de la fórmula del área en el teorema anterior
depende solamente de la continuidad de f y g y del supuesto de que g (x)  f (x). No
depende de las posiciones de las gráficas de f y g con respecto al eje x .
Si las gráficas de las figuras se localizan por encima del eje x , podemos interpretar
geométricamente el área de la región entre las gráficas como el área de la región situada debajo de
la gráfica de f menos el área de la región situada debajo de la gráfica de g , como se muestra
en la figura.
Utilizaremos el mismo procedimiento que se usó para encontrar el área bajo una curva. Se
aproximará el área entre las dos curvas haciendo una partición del intervalo [a,b] en n subintervalos
de longitud (b-a)/n. En cada subintervalo escogemos un valor particular de x, al que llamaremos x*.
1. Evaluamos f(x*) y g(x*) y formamos rectángulos de base (b-a)/n y de altura f(x*)-g(x*) (si
f(x*)>g(x*)).
2. El área de dicho rectángulo es (f(x*)-g(x*))((b-a)/n). Al sumar las áreas de los rectángulos
obtenemos una aproximación al valor del área entre las curvas.
3. Tomando el límite cuando n--->Infinito obtendremos el valor exacto del área buscada.
4. Por definición, el límite de la sumatoria de Riemann es la integral definida de f(x)-g(x) en
[a,b].
5. Si g(x)>f(x) en alguna parte del intervalo, entonces la altura de los rectángulos es g(x*)-
f(x*).
Ejemplo 3. 1
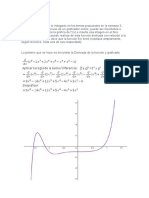
Hallar el área de la región limitada por las gráficas de f ( x)  2  x 2 y g ( x)  x.

28
(Dos gráficas que se cortan)
Vemos que las gráficas f y g tienen dos puntos de intersección. Para hallar las coordenadas
x de estos puntos, igualamos f (x) con g (x) y despejamos a x .
2  x2  x
 x2  x  2  0
 x  2x  1  0
Por tanto a  2 y b  1 . Por ser g (x)  f (x) en el intervalo  1, 1 . Por tanto el área de
la región es:
1
 x3 x2 
A
1
2
2  x  
2
 x dx   
 1 1   8  9
 2 x      2      2  4  
 3 2  2  3 2   3  2
Ejemplo 3. 2
Hallar el área de la región limitada por las gráficas de y  x 2  2 , y  x , x  0 y x  1 .
(Región delimitada por dos gráficas que no se cortan)
Por el teorema mencionado anteriormente el área de la región es:
1
 x3 x 2 
b
a
1
0
 2
  1
0
 2

A    f ( x)  g ( x)dx   x  2  ( x) dx   x  x  2 dx     2 x     2 
1 1 17
3 2 0 3 2 6
Ejemplo 3.3
Calcular el área de la región situada entre las gráficas de f ( x)  x 3  2 x 2  x  1 y

g ( x)   x 2  3x  1.

29
Para hallar las coordenadas x de estos puntos, igualamos f (x) con g (x) y despejamos a x
.
x 3  2 x 2  x  1   x 2  3x  1
x 3  2 x 2  x 2  x  3x  1  1  0

x x2  x  2  0 
xx  2x  1  0
Por tanto los puntos de corte son x  0, x  2, x  1.
Podemos apreciar en la figura que g (x)  f (x) en  1, 0 , sin embargo las curvas se cruzan
en el punto 0,1 y f ( x)  g ( x) en 0, 2 .
Entonces
   
A  1  f ( x)  g ( x) dx  0 g ( x)  f ( x) dx  1 x 3  x 2  2 x dx  0  x 3  x 2  2 x dx 
0 2 0 2
0 2
 x4 x3 2  x4 x3  1 1   8  37
   x      x 2      1    4   4  
4 3  1  4 3 0 4 3   3  12
Ejemplo 3. 4
Calcular el área de la región limitada por la gráficas de x  3  y y y  x  1 Imaginemos que

2
rebanamos esta región en dirección vertical. Afrontamos el problema de que el límite inferior consta
de dos curvas diferentes. Las rebanadas del extremo izquierdo se extienden de la rama inferior de
la parábola a la recta. (ver figura)

30
y

        




( AR1  Rebanadas del extremo izquierdo)

Las rebanadas del extremo derecho se extienden de rama inferior de la parábola a su rama
superior.(ver figura)
y

        




( AR 2  Rebanadas del extremo derecho)

Resolver este problema con rebanadas verticales requiere que dividamos primero nuestra región
en dos partes, formulemos una integral para cada parte y evaluemos después ambas integrales.
Primero necesitamos los puntos de intersección de estas dos curvas. Luego las coordenadas de
estos puntos se pueden encontrar igualando las dos expresiones:
3  x  x  1
2
3  x  x 2  2x  1
x 2  2x  1  3  x  0
x2  x  2  0

31
x  2x  1  0
Por tanto los puntos de corte son x  2, x  1.
Sea f (x)  x  1 y sea g ( x)   3  x

Podemos apreciar en la figura que g (x)  f (x) en  1, 3
A  AR1  AR 2  1  f ( x)  g ( x) dx  2  f ( x)  g ( x) dx 

2 3
Entonces
    3  x   3  x dx 
1  x  1   3  x dx  2
2 3
2
1  x  1  3  x dx    3  x  3  x dx 
3
2
2
1  x  1 dx   3  xdx    3  x dx   3  xdx 
2
1
3
2
3
2
     32 3  x  
2
 x2 
  x  3  x  3  x 2
2 3 2 2 3 3 3 3
1 
2 2
2 2
 2  1 3 3
1  2
   1  1  8  0  1  0  1      
2 2 3 14 2 2 9
2  3 3 3 2 3 3 3 2
En general, para determinar el área entre dos curvas, hacemos:
A  x12 curva de arriba   curva de abajo  dx  Rectángulos verticales

x
Si la gráfica de una función de y es el borde de una región, con frecuencia es conveniente usar
rectángulos representativos horizontales y calcular el área integrando respecto a y .
A  y12 curva derecha   curva izquierda dy  Rectángulos horizontales

y
Luego el ejercicio anterior se puede realizar de una manera más sencilla, es decir, tomando
rectángulos representativos horizontales, así:
Estas curvas se cortan en y  2, y  1. Como f ( y)  g ( y) tenemos que:

1
 y3 y2 
A
1
2
 3  y 2
 1
2

  y  1 dy    y  y  2 dy    2
 2 y  
 3 2  2
 1 1  8 2  9
   2     4 
 3 2  3 2  2
Ejemplo 3. 5. Hallar el área de la región limitada por las gráficas de f ( x)  3x3  x2  10 x y
g ( x)   x 2  2 x
3 2 2
f(x)= 3x - x - 10x g(x)= - x + 2x

32
Se encuentran los puntos de corte igualando las ecuaciones f ( x)  g ( x )
3x3  x2  10 x   x2  2 x
3x3  12 x  0
3x( x  2)( x  2)  0
Entonces los puntos de corte son x  0 , x  2 y x  2
Para encontrar el área se tiene en cuenta los puntos de corte y por la gráfica se observa la curva
que está por arriba y la que está por debajo, además se encuentran dos áreas asi:
 (3x   
0 2
A  A1  A2  3
 x 2  10 x)  ( x 2  2 x) dx   ( x 2  2 x)  (3x3  x 2  10 x) dx
2 0
 3x   
0 2
A 3
 12 x dx   12 x  3x3 dx
2 0
A =0
3. 2 Volúmenes de Sólidos de Revolución
Al tratar de hallar el volumen de un sólido enfrentamos el mismo tipo de problema que el de buscar
áreas. Este tipo de sólidos suele aparecer frecuentemente en ingeniería y en procesos de
producción. Son ejemplos de sólidos de revolución: ejes, embudos, pilares, botellas y émbolos.

33
Si giramos una región del plano alrededor de una línea, el sólido resultante es conocido como
sólido de revolución y la línea como eje de revolución.
3.2.1 Método de discos y arandelas
El más simple de los sólidos de revolución es el cilindro circular recto o disco, que se forma al girar
un rectángulo alrededor de un eje adyacente a uno de los lados del rectángulo.
Para calcular el volumen de un sólido de revolución por el método de discos, se usa una de las
siguientes fórmulas:
Eje horizontal de revolución Eje vertical de revolución
V   a R( x) dx  V   c R( y) dy

b 2 d 2
Volumen Volumen
Si la región limitada por un semicírculo y su diámetro gira en torno a éste, genera un sólido
esférico. Si la región interior de un triángulo rectángulo gira alrededor de uno de sus catetos,
genera un sólido cónico. Cuando una región circular gira alrededor de una recta en un plano que
no intercepta al círculo genera un toro (o una dona). En cada caso, es posible representar el
volumen como una integral definida.
Ejemplo 3.6
Hallar el volumen de un sólido formado al girar la región limitada por la gráfica de f ( x)  sin x
y el eje x 0  x    alrededor del eje x.
(Región plana)
Del rectángulo representativo de la figura anterior se observa que el radio de este sólido viene
dado por:
R( x )  f ( x )  sin x
y se sigue que su volumen es:
V   a R( x) dx   0
b 2 
 sin x  dx
2
  0 sin xdx   cos x0   1  1  2
 
Sólido de revolución

34
Ejemplo 3.7
Hallar el volumen del sólido generado por la rotación de la región limitada por la curva y  x 3 el
eje de las y y la recta y  3 en torno al eje de las y .
(Región plana)
Aquí rebanamos horizontalmente, lo que hace que y sea la elección apropiada para la variable de
yx equivale a x  3 y . Luego la integral quedaría:
3
integración. Observe que
 y  dy
3
2 3 5  93 9
V      y 3  dy  
1
3 3
0
5  0 5
3.2.2 Método de cascarones cilíndricos
Hay otro método para encontrar el volumen de un sólido de revolución: el método de cascarones
cilíndricos o envolventes. En muchos casos, es mejor utilizar los métodos vistos anteriormente
(discos y arandelas)
Un cascarón cilíndrico es un sólido limitado por dos cilindros circulares rectos concéntricos. Si el
radio interior es r 1 , el exterior es r 2 y la altura es h , entonces el volumen está dado por:
 
V  área de la basealtura   r22  r12 h   r2  r1 r2  r1  h  2  hr
r2  r1
2 2  r1  Por
tanto:
V  2 radio medio altura grosor 
V  2rhr
Ejemplo 3.8
La región limitada por y  1 / x , el eje de las x , x  1 , x  4 gira alrededor del eje de las x
Encuentre el volumen del sólido resultante.

35
V  2 1 x
4
 dx  2  x
1
x 1
4
1
2
dx  2  x  
2
3
3
2
4
1
28
3  29.32
3.2.3 Volumen por Secciones Transversales

Hasta aquí los sólidos vistos han tenido secciones transversales circulares. Sin embargo, nuestro
método funciona también para sólidos cuya sección transversal son cuadrados o triángulos. En
realidad lo único que se necesita es calcular el área de la sección trasversal.
Ejemplo 3.9
y  1  x4 , el eje de las
2
La base de un sólido es la región plana del primer cuadrante limitada por
x y el eje de las y. Suponga que las secciones transversales perpendiculares al eje de las x
son cuadradas. Encuentre el volumen del sólido.
Cuando rebanamos este sólido mediante planos perpendiculares al eje de las x , se obtienen
delgadas cajas cuadradas.

36
2
 x2 x4   x3 x5  8 32 16
V   1    dx   x     2     1.07
2
0
 2 16   6 80  0 6 80 15
Ejemplo 3.10
La base de un sólido es la región comprendida entre el arco de y  sin x y el eje de las x .

Cada sección transversal perpendicular al eje de las x es un triángulo equilátero apoyado sobre
su base. Encuentre el volumen del sólido.
Necesitamos conocer el área del triángulo equilátero. Entonces supongamos que u es el lado del
triángulo equilátero, luego el área va a ser igual a 3 u 2 /4 (veamos en la figura)
A 1
2
u u  
2
3
3u 2 14  3u 2 / 4

37
Para realizar la integración indicada, usamos la fórmula de ángulo medio sin 2 x  1  cos 2 x  / 2
3  3  3  1cos 2 x
V  u dx 
4 0
2
4 0 sin xdx 
2

4 0 2 dx 
 1  cos 2 x  dx 
3  3 
 sin xdx 
2
4 0 8 0
8
3
 1dx 

0
1 
 cos 2 xdx 
2 0

8
3
x  12 sin 2x0 
8
3
  0.68

38
UNIDAD 4 COORDENADAS POLARES
Definición 4.1 Sistema de coordenadas polares
Las coordenadas polares o sistemas polares son un sistema de coordenadas bidimensional en el

cual cada punto del plano se determina por un ángulo ϴ y una distancia r
4.2 Representación de Puntos en el Plano Polar
Se traza una circunferencia de radio r y centro O, se dibuja el ángulo ϴ, con lado inicial el eje polar.
El punto de intersección de la circunferencia y el lado terminal del ángulo ϴ, corresponde al punto
de coordenadas P(r, ϴ)
Ejemplos 4.1
a) El punto (3, 60º) indica que está a una distancia de 3 unidades desde O, medidas con un ángulo
de 60º sobre OL.
b) El punto (4, 210º) indica que está a una distancia de 4 unidades desde O y un ángulo de 210º
sobre OL.

39
4. 3 Coordenadas Polares y Cartesianas
A partir de la siguiente gráfica podemos establecer las relaciones que se establecen entre la
representación en coordenadas cartesianas y polares.
a)
b)
c)
d)
Ejemplos 4.2
a) El punto en coordenadas polares P (2, 30º) convertirlo a coordenadas cartesianas
x= 2 cos 30º, x= 1,7
y= 2 sen30º, y = 1
b) El punto en coordenadas cartesianas P (1, -2)
2 2 ½
r= ((1) + 2 ) r= 2.2
-1
ϴ = tan (-2/1) = -63.4°
4.4 Ecuaciones polares
Se le llama ecuación polar a la ecuación r = f (ϴ) que define una curva expresada en coordenadas
polares.
La curva resultante consiste en una serie de puntos en la forma ( (θ), θ) y se puede representar

40
como la gráfica de una función .
Ejemplos 4.3
a) Circunferencias: r= asen ϴ; r = acos ϴ¸
b) Cardioides: r= a+b sen ϴ ; r= a+b cos ϴ
c) rosas: r= asenk ϴ ; r= acos k ϴ
Para hacer la representación gráfica de una curva se hace una tabla de algunas coordenadas y
se representan los puntos en el plano polar.
ϴ r= sen2
ϴ
0 0
45° 1
90° 0
135° -1
180° 0
225° 1
270° 0
315° -1
360° 0
La gráfica obtenida es:

41
4.5 Área de curvas polares
Sea R una región del plano delimitada por la curva continua r(θ) y las semirrectas θ = a y θ = b,
donde 0 < b − a < 2π. Entonces, el área de R viene dado por
l intervalo [a, b] se divide en n subintervalos, donde n es un entero positivo cualquiera. Por lo tanto
Δθ, la longitud de cada subintervalo, es igual a b − a (la longitud total del intervalo) dividido por n (el
número de subintervalos). Para cada subintervalo i = 1, 2, …, n, sea θi su punto medio. Se puede
construir un sector circular con centro en el polo, radio r(θi), ángulo central Δθ y longitud de arco
. El área de cada sector es entonces igual a
Por lo tanto, el área total de todos los sectores es
En el límite, cuando n → ∞, converge en la integral
Ejemplos 4.4
a) hallar el área de la región encerrada por la curva r= sen 2 θ , como la gráfica está formada por 4
pétalos, hallamos el área de un pétalo y lo multiplicamos por 4.

42
El área es igual a 1.57 unidades cuadradas.
b. Hallar el área dentro de la curva r= 2 y fuera de la curva r= 1+senϴ
- Hallamos el punto de corte de las curvas igualando las ecuaciones:
2= 1+senϴ, se tiene que senϴ = 1 por tanto ϴ= π/2

43
BIBLIOGRAFÍA
LARSON, Edwards, Cálculo Sexta Edición. España: McGraw Hill, 1998.
PURCELL, Vargerg Rigdon. Cálculo Novena Edición. México: Pearson Hill Educación, 2007.
STEWART, James. Cálculo Trascendente Temprano, Sexta Edición. México: Cengage Learning,
2008.

Apuntes Docentes PDF

Încărcat de

Informații document

Titlu original

Drepturi de autor

Formate disponibile

Partajați acest document

Partajați sau inserați document

Opțiuni de partajare

Vi se pare util acest document?

Este necorespunzător acest conținut?

Drepturi de autor:

Formate disponibile

Apuntes Docentes PDF

Încărcat de

Drepturi de autor:

Formate disponibile

1

APUNTES DOCENTES DE CÁLCULO INTEGRAL

YASMITH BOCANEGRA ARAGON

MARISEL ARDILA AMADOR

DEPARTAMENTO DE CIENCIAS BÁSICAS

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

1.1 Anti derivada o primitiva. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ………. 5

1.2 Integral Indefinida……………... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

1.3 Área de una región en el plano. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

1.4 Sumatoria . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ... . . . . . 9

1.4.1 Propiedades de la Sumatoria. . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . ..9

1.5 Partición de un intervalo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1.6 Suma de Riemann. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .... 10

1.7 Integral Definida. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.8 Área e integral definida. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10

1.8.1 Propiedades de la integral definida. . . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . . . . . .10

1.8.2 Primer teorema Fundamental del Cálculo. . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . .15

1.8.3 Segundo teorema Fundamental del Cálculo... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

1.8.4 Teorema del valor Medio. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 16

1.9 Valor Promedio. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

2. TÉCNICAS DE INTEGRACIÓN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19

2.1 Regla de la Sustitución Simple. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19

2.2 Integración por Partes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . .20

2.3 Integración de Funciones Trigonométricas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

2.4 Sustitución Trigonométrica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

2.5 Integración por Fracciones Parciales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

3.1 Área entre Curvas: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

3.2 Volúmenes de Sólidos de Revolución. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 32

3.2.1 Método de Discos y Arandelas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

3.2.2 Método de Cascarones Cilíndricos. . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . .. ... 34

3.2.3 Volumen por Secciones Transversales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . .35

4.1 Sistema de Coordenadas s Polares. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .38

4.2 Representación de Puntos en el Plano Polar. . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 38

4.3 Coordenadas Polares y Cartesianas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

4.4 Ecuaciones Polares... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 39

4.5 Área entre Curvas Polares. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

Esta asignatura contribuye a desarrollar un pensamiento lógico, heurístico y algorítmico al modelar

Buscando la comprensión del signiﬁcado de la integral se propone un tratamiento que comience

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

Definición 1.1 Anti derivada o primitiva

Se dice que la función F es una anti derivada o primitiva de f , en un intervalo I si y solo si

Si F es una anti derivada de f en un intervalo I, entonces G es una anti derivada de f en el intervalo

A continuación se presentan las antiderivadas de algunas funciones:

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

Definición 1.2 Integral Indefinida

La integral indefinida de la función f con respecto a x es igual a la anti derivad de f.

Escribamos la integral definida de las funciones reales básicas.

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

Halle las siguientes integrales indefinidas:

Definición 1.3 Área de una región en el plano

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

xi  a  ix,..., xn1  a  (n  1)x, xn  b . Asimismo, se denota el i-ésimo intervalo por

f mi   valor mínimo de f (x) en el i-ésimo intervalo

Sumando estas dos áreas, tenemos

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

Definición 1.4 Sumatoria

Teorema 1.4.1 Propiedades de la Sumatoria:

Definición 1.5 Partición de un Intervalo cerrado:

APUNTES DOCENTES DE CÁLCULO INTEGRAL 2014

Definición 1.6 Suma de Riemann:

Donde  i es un punto cualquiera del i  ésimo subintervalo y,  i x es la longitud de este