Documente Academic
Documente Profesional
Documente Cultură
Probability Normal Distribution
Încărcat de
Hayati Aini AhmadDescriere originală:
Drepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
Probability Normal Distribution
Încărcat de
Hayati Aini AhmadDrepturi de autor:
Formate disponibile
Normal Distribution Form 5
PAPER 1(SET 1) 1. X is a random variable of a normal distribution with a mean of 6.4 and a variance of 1.96. Find (a) (b) 2. the z-score if [1.5] [0.4332] and a
X is a continuous random variable of a normal distribution with a mean of standard deviation of . Find (a) (b) the Z-score when the value of if [-1.175] [-0.524] when [1.4] [-1.96]
[4 marks]
3.
Find the value of (a) (b)
[4 marks] and a variance of
4.
is a random variable of a normal distribution with a mean of . Find (a) the z-score if [0.5] (b)
[0.4235]
[4 marks]
5.
is a random variable which is normally distributed with mean Find (a) (b) the value of given that the z-score is 1.5 when
and variance 16.
[ 65] [3 marks] and a
[0.0668]
6.
X is a continuous random variable of a normal distribution with a mean of standard deviation of . Find (a) (b) the Z-score when the value of when [3.04] [1.13]
[4 marks]
7.
The masses of watermelons produced by an orchard have a normal distribution with a mean of 3.2 kg and a standard deviation of 0.6 kg. (a) (b) Find the mass, in kg, of a watermelon whose Z-score is [2.9]
If a watermelon is chosen at random, find the probability that the watermelon has a mass of at least kg.[0.7734] [4 marks]
Prepared by : Puan Hayati Aini Ahmad
Page 1
Normal Distribution Form 5
8. The heights of a group of students in SMK Bandar Baru Selayang have a normal distribution with mean of cm and a standard deviation of cm. Calculate the probability that a student chosen at random from this group (a) (b) 9. is taller than cm[0.1587] [4 marks]
is between 147 cm and 165.8 cm tall[0.7528]
The height of employees in a company has a normal distribution with a mean of 160 cm and a standard deviation of 10 cm. Find (a) (b) the height of employees which gives a standard score of 0.8.[168] the percentage of employees with height greater than 155 cm[69.15%]
10.
The masses of students in a class normally distributed with a mean of 50 kg and a standard deviation of 1.2 kg. Find (a) (b) the mass, in kg, which is equivalent to the standard score of 0.6.[50.72] the percentage of students that have a mass of less than 48 kg.[4.78%]
11.
The masses of students in a school have a normal distribution with a mean of 50 kg and a standard deviation of 8 kg. Find (a) (b) the masses of students which gives a standard score of 0.75[56] the percentage of students with mass greater than 38 kg.[93.32%] [3 marks]
12.
The mass of the residents in Kampung Manis is found to be normally distributed with mean 52 kg and standard deviation 8 kg. Calculate (a) (b) the probability that the mass of a resident chosen at random is more than 56 kg.[0.3085] the value of , if 5% of the residents have mass of less than kg.[38.84]
13.
The mass of durians collected in an orchard has a normal distribution with a mean of g and a standard deviation of g. The probability that a durian is chosen at random with a mass greater than g is . (a) (b) Find the value of [3094]
A total of 4 600 durians are collected. Find the number of durians with mass greater than g [115] [4 marks]
14.
The heights of a group of students, in cm, are normally distributed with a mean of and a standard deviation of . If 8.08% of the students have heights exceeding 168 cm and 15.87% of the students have heights less than 160 cm, find the value of and .[163.33 ; 3.333]
Page 2
Prepared by : Puan Hayati Aini Ahmad
Normal Distribution Form 5
PAPER 1(SET 2) 1. 2. Given that , find the value of . [2 marks]
If X is a random variable of normal distribution with a mean of 25 and a variance of 1.72, find (a) the Z-value if if [1.25] [0.2] [4 marks] [2.211] (b) [0.6062]
3.
Find the value of (a) (b)
4.
The mass, in kg, of the students in a school are normally distributed with a mean of 45 kg and a variance of 9 kg2. Find the standard score for the mass of 48 kg.[1] X is a random variable of a normal distribution with mean of 4.8 and a variance of 2.25. Find (a) (b) the z-score if [1.2] [0.72627]
5.
6. 7.
If the random variable X has a normal distribution with mean 45 and standard deviation and , find the value of .[10.73] The mass of students in a school has a normal distribution with a mean 60 kg and a standard deviation of 10 kg. Find (a) (b) the mass of the students which gives a standard score of 0.25 the percentage of students with mass greater than 55 kg.
8.
The mass, in kg, of the students in a school are normally distributed with a mean of 60 kg and a variance of 25 kg2. Find the mass that corresponds to the Z-score of .[61]
9.
M is a random variable of normal distribution with a mean of 120 and a variance of 100. Find (a) (b) the Z-score if M=100
10.
The ages, in years, of the members of a squash club are found to be normally distributed with a mean of 48 and a standard deviation of 6. Find the probability that a member chosen at random will have an age between 45 and 52.[0.4392]
Page 3
Prepared by : Puan Hayati Aini Ahmad
Normal Distribution Form 5
11. Find the value of (a) 12. if [0.24] (b) [0.94]
X is a random variable of a normal distribution with a mean of 12.45 and variance of 9. Find (a) (b) the value of if [0.2747] [14.805]
13.
The life span of a battery is normally distributed with a mean of 200 days and standard deviation of 30 days. Find (a) (b) the life span in days, which is equivalent to the standard score of -2[140] the percentage of batteries that have a life span of more than 180 days.[74.52%]
14.
The marks for the Physics test of the students in a class are found to be normally distributed with a mean of 55 and a standard deviation of 10. If the range of marks to obtain a credit is from 50 to 70, calculate the percentage of students who obtained a credit.[62.47%] Find the value of (a) (b) if [1.14] [0.82]
15.
16.
X is a continuous random variable of a normal distribution with a mean of 28 and a standard deviation of 4. Find (a) (b) the z-score when the value of when [1.125] [-0.723]
17.
A normal distribution has a mean of 5 and a standard deviation of 2. Calculate the standard score if [0.9] The mass of durians produced in an orchard is normally distributed with a mean of 950 g and a standard deviation of 140 g. If a durian is picked at random, calculate the probability that its mass is between 790 g and 1 030 g.[0.5895]
18.
Prepared by : Puan Hayati Aini Ahmad
Page 4
Normal Distribution Form 5
PAPER 1(SET 3) 1.
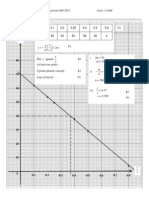
Diagram above shows a standard normal distribution graph. The probability represented by the area of the shaded region is 0.2881. (a) (b) Find the value of [0.8] X is a continuous random variable which is normally distributed with a mean of 80 and a standard deviation of 5. Find the value of when the z-score is .[84]
f(z)
2.
0 -k k
Diagram above shows a standardised normal distribution graph. If , find .[0.296]
Prepared by : Puan Hayati Aini Ahmad
Page 5
Normal Distribution Form 5
3.
Diagram above shows a standardised normal distribution graph. The probability represented by the shaded region is 0.2846. (a) (b) Find the value of .[0.788] If X is a continuous random variable of a normal distribution with a mean of 68 and a standard deviation of 5, find the value of X when its z-score is .[64.06]
4.
f(z)
0 k
If 5.
, find
.[0.3352]
Prepared by : Puan Hayati Aini Ahmad
Page 6
Normal Distribution Form 5
If 6. , find the value of [0.7896]
The probability represented by the area of the shaded region is 0.3925. (a) (b) Find the value of [1.24] X is a continuous random variable which is normally distributed with a mean of 72 and a standard deviation of 4. Find the value of X when the Z-score is .[67.04]
7.
The probability represented by the area of the shaded region is 0.1554. (a) (b) Find the value of [0.4] X is a continuous random variable which is normally distributed with a mean of and a standard deviation of . Find the value of X when the z-score is .[162.4] [4 marks]
Prepared by : Puan Hayati Aini Ahmad
Page 7
Normal Distribution Form 5
8.
Diagram above shows a standardised normal distribution graph. If 9. , find
If 10.
, find
Given that
, find the value of [0.4]
Prepared by : Puan Hayati Aini Ahmad
Page 8
S-ar putea să vă placă și
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDe la EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeEvaluare: 4 din 5 stele4/5 (5795)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDe la EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreEvaluare: 4 din 5 stele4/5 (1091)
- Never Split the Difference: Negotiating As If Your Life Depended On ItDe la EverandNever Split the Difference: Negotiating As If Your Life Depended On ItEvaluare: 4.5 din 5 stele4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDe la EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceEvaluare: 4 din 5 stele4/5 (895)
- Grit: The Power of Passion and PerseveranceDe la EverandGrit: The Power of Passion and PerseveranceEvaluare: 4 din 5 stele4/5 (588)
- Shoe Dog: A Memoir by the Creator of NikeDe la EverandShoe Dog: A Memoir by the Creator of NikeEvaluare: 4.5 din 5 stele4.5/5 (537)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDe la EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersEvaluare: 4.5 din 5 stele4.5/5 (345)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDe la EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureEvaluare: 4.5 din 5 stele4.5/5 (474)
- Her Body and Other Parties: StoriesDe la EverandHer Body and Other Parties: StoriesEvaluare: 4 din 5 stele4/5 (821)
- The Emperor of All Maladies: A Biography of CancerDe la EverandThe Emperor of All Maladies: A Biography of CancerEvaluare: 4.5 din 5 stele4.5/5 (271)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)De la EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Evaluare: 4.5 din 5 stele4.5/5 (121)
- The Little Book of Hygge: Danish Secrets to Happy LivingDe la EverandThe Little Book of Hygge: Danish Secrets to Happy LivingEvaluare: 3.5 din 5 stele3.5/5 (400)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDe la EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyEvaluare: 3.5 din 5 stele3.5/5 (2259)
- The Yellow House: A Memoir (2019 National Book Award Winner)De la EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Evaluare: 4 din 5 stele4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDe la EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaEvaluare: 4.5 din 5 stele4.5/5 (266)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDe la EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryEvaluare: 3.5 din 5 stele3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnDe la EverandTeam of Rivals: The Political Genius of Abraham LincolnEvaluare: 4.5 din 5 stele4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealDe la EverandOn Fire: The (Burning) Case for a Green New DealEvaluare: 4 din 5 stele4/5 (74)
- The Unwinding: An Inner History of the New AmericaDe la EverandThe Unwinding: An Inner History of the New AmericaEvaluare: 4 din 5 stele4/5 (45)
- KMC 2014 School List Registration v1-1Document15 paginiKMC 2014 School List Registration v1-1Hayati Aini AhmadÎncă nu există evaluări
- Index Number - Set 2@2010Document2 paginiIndex Number - Set 2@2010Hayati Aini AhmadÎncă nu există evaluări
- Linear Law 2014Document8 paginiLinear Law 2014Ainol Bazlin FarhanaÎncă nu există evaluări
- Integration and DifferentiationDocument7 paginiIntegration and DifferentiationHayati Aini AhmadÎncă nu există evaluări
- Jom Tanya Sifu@Form 5: Chapter 1: PROGRESSIONSDocument15 paginiJom Tanya Sifu@Form 5: Chapter 1: PROGRESSIONSHayati Aini Ahmad100% (1)
- Index Number Set3@2010Document2 paginiIndex Number Set3@2010Hayati Aini AhmadÎncă nu există evaluări
- Module 11 (B) Add Math - Index NumberDocument10 paginiModule 11 (B) Add Math - Index NumberHayati Aini AhmadÎncă nu există evaluări
- Module 8A - Circular MeasureDocument11 paginiModule 8A - Circular MeasureHayati Aini Ahmad100% (2)
- Solutions of Triangle - Set 2Document2 paginiSolutions of Triangle - Set 2Hayati Aini AhmadÎncă nu există evaluări
- 3472 MT - Skema Kertas 2no.7Document1 pagină3472 MT - Skema Kertas 2no.7Hayati Aini AhmadÎncă nu există evaluări
- 3472 MT - Skema Kertas 2no.14Document1 pagină3472 MT - Skema Kertas 2no.14Hayati Aini AhmadÎncă nu există evaluări
- MT k2 Marking Scheme 2010Document8 paginiMT k2 Marking Scheme 2010Hayati Aini AhmadÎncă nu există evaluări
- Module 10B - Solution of TrianglesDocument9 paginiModule 10B - Solution of TrianglesHayati Aini AhmadÎncă nu există evaluări
- Circular Measure@Set 1Document2 paginiCircular Measure@Set 1Hayati Aini AhmadÎncă nu există evaluări
- 15 Days Programme Part 3Document15 pagini15 Days Programme Part 3Basri JaafarÎncă nu există evaluări
- 1.PTSP SyllabusDocument2 pagini1.PTSP SyllabusSaivenkat BingiÎncă nu există evaluări
- MIE1605 1b ProbabilityReview PDFDocument96 paginiMIE1605 1b ProbabilityReview PDFJessica TangÎncă nu există evaluări
- Chapter 3: Some Special Distributions: Phan Thi Khanh VanDocument79 paginiChapter 3: Some Special Distributions: Phan Thi Khanh VanHuỳnh Nhật HàoÎncă nu există evaluări
- ProbabilityDocument78 paginiProbabilitylupus359Încă nu există evaluări
- Probability and Statistics Module 1Document24 paginiProbability and Statistics Module 1Jude MetanteÎncă nu există evaluări
- Table 1: Cumulative Normal DistributionDocument1 paginăTable 1: Cumulative Normal DistributionMohamaad SihatthÎncă nu există evaluări
- Newbold Sbe8 Tif ch05 PDFDocument58 paginiNewbold Sbe8 Tif ch05 PDFak100% (1)
- Normal To Binomial ApproximationDocument2 paginiNormal To Binomial ApproximationTito Bayu ArtomoÎncă nu există evaluări
- m4 PDFDocument23 paginim4 PDFSantosh SanthuÎncă nu există evaluări
- Lesson 11:: Expected Value of Random VariablesDocument20 paginiLesson 11:: Expected Value of Random VariablesNyah MargarettÎncă nu există evaluări
- Les4e Alq 04acDocument17 paginiLes4e Alq 04acsai raoÎncă nu există evaluări
- MartingalesDocument40 paginiMartingalesSidakpal Singh SachdevaÎncă nu există evaluări
- QT - Bba - Module Iv - JurazDocument6 paginiQT - Bba - Module Iv - JurazMohammed Shalbin mpÎncă nu există evaluări
- Course Notes Stochastic Processes - AucklandDocument195 paginiCourse Notes Stochastic Processes - AucklandRR886Încă nu există evaluări
- AnalysisDocument3 paginiAnalysisLau MerchanÎncă nu există evaluări
- Session 4Document41 paginiSession 4Aditi BadwayaÎncă nu există evaluări
- Quiz On Normal DistrributionDocument2 paginiQuiz On Normal Distrributiongulafshan100% (1)
- Probabilty DistributionsDocument7 paginiProbabilty DistributionsK.Prasanth KumarÎncă nu există evaluări
- TA: Yury Petrachenko, CAB 484, Yuryp@ualberta - Ca, HTTP://WWW - Ualberta.ca/ YurypDocument6 paginiTA: Yury Petrachenko, CAB 484, Yuryp@ualberta - Ca, HTTP://WWW - Ualberta.ca/ YurypMotseilekgoaÎncă nu există evaluări
- Full Download Solutions Manual To Accompany Stochastic Calculus For Finance I 9780387249681 PDF Full ChapterDocument34 paginiFull Download Solutions Manual To Accompany Stochastic Calculus For Finance I 9780387249681 PDF Full Chapterbriber.soordus2a4j100% (16)
- MIT18 05S14 Class4slides PDFDocument16 paginiMIT18 05S14 Class4slides PDFAftab SaadÎncă nu există evaluări
- LSU MATH 7311 Qual QuestionsDocument39 paginiLSU MATH 7311 Qual QuestionsHunter PattonÎncă nu există evaluări
- 2.7 Correlation Coefficient and Bivariate Normal DistributionDocument11 pagini2.7 Correlation Coefficient and Bivariate Normal DistributionPawan NayakÎncă nu există evaluări
- SI Lec 5Document5 paginiSI Lec 5Muhammad Rafeeq0% (2)
- BIOSTAT Random Variables & Probability DistributionDocument37 paginiBIOSTAT Random Variables & Probability DistributionAnonymous Xlpj86laÎncă nu există evaluări
- Table Common DistributionsDocument3 paginiTable Common DistributionsAndrew GoodÎncă nu există evaluări
- MA6451 Probability and Random ProcessDocument59 paginiMA6451 Probability and Random ProcessPrajwal BirwadkarÎncă nu există evaluări
- Exploring Random Variables: Lesson 1Document18 paginiExploring Random Variables: Lesson 1Jaylou AntipuestoÎncă nu există evaluări
- MODULE 1: Probability DistributionsDocument2 paginiMODULE 1: Probability DistributionsS.L.L.CÎncă nu există evaluări
- IE 5004 Lecture 2Document45 paginiIE 5004 Lecture 2Prashant TolaniÎncă nu există evaluări