PHYSICAL REVIEW E 71, 066304 2005

Fast-convergent iterative scheme for ltering velocity signals and nding Kolmogorov scales
J. Mi, R. C. Deo, and G. J. Nathan
School of Mechanical Engineering, University of Adelaide, South Australia 5005, Australia Received 30 September 2004; published 13 June 2005 The present fundamental knowledge of uid turbulence has been established primarily from hot- and coldwire measurements. Unfortunately, however, these measurements necessarily suffer from contamination by noise since no certain method has previously been available to optimally lter noise from the measured signals. This limitation has impeded our progress of understanding turbulence profoundly. We address this limitation by presenting a simple, fast-convergent iterative scheme to digitally lter signals optimally and nd Kolmogorov scales denitely. The great efcacy of the scheme is demonstrated by its application to the instantaneous velocity measured in a turbulent jet. DOI: 10.1103/PhysRevE.71.066304 PACS number s : 47.27. i, 47.80. v

In his pioneering work 1 on turbulence, Kolmogorov derived, based on dimensional reasoning, the characteristic length of the nest-scale turbulent motions to be
3

1/4

It is important to note that the nonltered or slightly ltered velocity signals uim the subscript m means measured is inevitably contaminated by high-frequency electronic noise n , i.e., uim = ui + n. 7

which is hence called the Kolmogorov length scale. In Eq. 1 , is the kinematic viscosity and is the average dissipation rate of the turbulence kinetic energy given by e.g., Hinze 2 = u i/ x j + u j / x i u i/ x j 2

This contamination causes both the spatial and temporal gradient variances to be overestimated, i.e., uim/ x j 2 = uim/ t 2 = u i/ x j 2 + u i/ t 2 + n/ x j 2 , n/ t 2 . 8

with standard Cartesian tensor notation and summation on repeated indices, where i or j = 1, 2, and 3 represent the streamwise, lateral, and spanwise directions, respectively. The appropriate estimate of is of signicant importance for improving our understanding of the ne-scale turbulence. However, great difculty occurs in directly measuring this characteristic scale. To obtain requires all the 12 terms of gradient correlations in Eq. 2 to be measured. This task cannot be realized by presently available experimental techniques. Accurate measurements of even one component of ui / x j, as is well known, requires a multisensor probe with extremely high spatial and temporal resolution to incorporate even the smallest scales of velocity uctuations. Moreover, several cross-correlation terms in Eq. 2 simply cannot be measured directly now 3 or in the foreseeable future, let alone direct measurements of and . In this context, it remains necessary to estimate from hot-wire measurements of using the isotropic relation = 15 and also Taylors hypothesis u1/ x1 2 = U2 u1/ t 2 , 1 4 u 1/ x 1
2

where U1 is the local streamwise mean velocity. Substitution of Eq. 4 into Eq. 3 leads to = 15 U2 u1/ t 2 . 1 In addition, the Kolmogorov frequency is dened as fK U1 2
1

The extra terms n / x j 2 and n / t 2 are the unwanted noise contributions. Therefore, to achieve accurate measurements of the velocity gradients, it is necessary that the raw velocity signals uim be low-pass ltered at a specic cutoff frequency f c to eliminate the effect of noise. The choice of f c is critical. Too high and it will not remove noise contributions sufciently, while too low and it will wipe out some content of the signal. The right choice for f c is the Kolmogorov frequency f K, i.e., the characteristic frequency of the smallest structures. However, f K not only is a function of the ow but also varies with spatial locations in the ow so that it cannot be determined a priori. The method described in 4 to determine f c in situ is complex, requiring two mechanical analog lters, a differentiator, a real-time spectrum analyzer, visual inspection, and optimization at each measurement location. This procedure is only realistic where the number of spatial locations or ow conditions is limited, and is prohibitive for experiments where these are large. In the absence of a simpler procedure, more arbitrary criteria are usually adopted, so that most previous measurements of must be contaminated by noise to some extent. The importance of this issue is also evident from 5 from which it is deduced that even slightly over ltering uim at f c f K may cause substantial underestimate of the velocity gradients. From the above discussion it is obvious that substantial benet would arise from a procedure that could correctly obtain f K without prior knowledge of , or obtain both and f K solely from a nonltered signal of u1m. The present work aims to address this issue, i.e., to develop a simple and ef2005 The American Physical Society

1539-3755/2005/71 6 /066304 5 /$23.00

066304-1

MI, DEO, AND NATHAN

PHYSICAL REVIEW E 71, 066304 2005

fective scheme that can denitively obtain and f K from u1m t , and thus a means by which to low-pass lter all the velocity components uim t at f c = f K, thereby minimizing the effect of noise on gradients ui / x j and other derived quantities such as structure functions. Let us rst inspect the contributions of noise to the measured kinetic energy u2 and dissipation . This is illustrated 1 using the one-dimensional spectral forms of u2 and for 1 isotropy, which are see 6 u2 = 1
0

E1 k1 dk1

and = 15
0

k2E1 k1 dk1 , 1

10
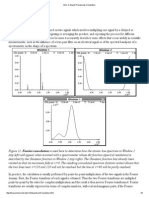
2 FIG. 1. Color online Power spectra of u1m and without noise contamination. m

respectively, where E1 is the one-dimensional spectrum function and k1 is the wave number in the streamwise x1 direction. To demonstrate the inuence of noise on u2 and , we 1 consider the model spectrum function e.g., 7,8 E1 k1 = CK 2/3k5/3 1 exp k1
3/4

with and

/C

1/4

= C1/4 .

16

11

Then, from Eq. 6 , we obtain f Km = C1/4 f K . 17

where CK is a constant determined empirically by experi3 ments and = 2 CK. Note that Eq. 11 has been veried by a large body of experimental high-Re data see 9 which references relevant experiments . Using Eq. 6 and k1 = 2 f / U1 Taylor hypothesis , Eq. 11 may be rewritten as E1 f = CK 2 /U1
5/3 5/3

exp

f/f K

3/4

12

Suppose the noise-contaminated velocity spectrum to be E1m = E1 + En, where En is the noise contribution. Then, from Eqs. 9 and 10 and k1 = 2 f / U1, we can obtain
2 u1m = 2 U1 1 0

E1 + En df

13

and
m

= 120

U3 1
0

f 2 E1 + En df .

14

Using Eq. 12 with CK = 1.7 and then = 2.55 e.g., 10 we 2 illustrate in Fig. 1 the spectral density distributions of u1m 3 2 and m with En = 0 and En = 10 f / f K . This demonstrates 2 that, when f c f K, the contributions of the noise to u1m and to m are very different. For example, if f c = 10f K, the ratios 2 u1m u2 / u2 and m / are approximately 3.3% and 1 1 2000%, respectively. This indicates that the high-frequency noise contamination, if not properly ltered out, has an ex2 tremely large impact on m while its inuence on u1m, or 2 more generally on uim, is very much less. Next we examine the effects of noise on the measured Kolmogorov scales m and f Km. Let us express the measured dissipation m by
m

= +

1+

n/

=C

15

1, where n denotes the noise contribuwith C = 1 + n / tion. Substituting Eq. 15 into Eq. 1 leads to

Accordingly, the error in m, m, or f Km from high-frequency noise can be measured by the departure of C p from unity. As seen from Eqs. 15 17 , the exponent p varies from p = 1 for m to p = 1 / 4 for m and f Km. This implies a much greater error for m than for m and f Km. For example, the case m = 5 results in an error of 400% overvalued , while the corresponding error is only 33% underestimated for m and 50% overestimated for f Km. It follows that, if we can relter uim at f Km calculated from Eq. 6 and then recalculate m, the noise part n or C 1 see Eq. 15 will reduce dramatically. Subsequent recalculations of m, f Km, and then m will further reduce their errors until m , m , and f Km f K. In principle, this analysis does not require any assumptions such as isotropy or Taylors hypothesis. That is, were the true or all terms of Eq. 2 measurable, it would result in such an iterative scheme by which all noise contaminations of uim i = 1 , 2 , 3 can be optimally ltered and therefore by which the true , , and f K can be found from postprocessing of sampled signals of uim. However, since the direct measurement of is impossible at present, and in the foreseeable future, this scheme currently can be implemented only by invoking the isotropy assumption Eq. 3 and Taylors hypothesis Eq. 4 . Here we propose it in Fig. 2 and provide more details below. 0 The original velocity signal U1m t is measured by a hotwire probe and sampled at a very high frequency 20 kHz, say . Application of analog lters is not necessary, i.e., no ltering is needed f c0 = . Otherwise, use a high cutoff 0 frequency f c0 . With the signal collected, rst calculate m 0 from Eq. 5 and then m from Eq. 1 . Next, substituting 0 0 0 0 0 , where m into Eq. 6 results in f Km. If f c f Km / f c is a threshold of convergence and should be small, say, 0 0 103 , lter u1m at f c1 = f Km digitally using, e.g., MATLAB.

066304-2

FAST-CONVERGENT ITERATIVE SCHEME FOR

PHYSICAL REVIEW E 71, 066304 2005

FIG. 2. Iterative scheme of and f K digital lter to obtain from u1m.

1 The newly ltered velocity signal u1m is thus generated. The above process may be repeated as many times as 2 3 N necessary to generate u1m , u1m , . . . , u1m , and then 2 3 N N N u1m / t , u1m / t , . . . , u1m / t, until f c f Km / f cN or N N N until f Km, m , and m have converged satisfactorily. From N N the converged data, we nally obtain = m , f K = f Km, and N = m . i i Based on Eqs. 15 17 , both f Km and m should converge quickly to their respective asymptotic values. This is true as demonstrated as an example in Table I for the case of f c0 = 10f K, with reference to Figs. 1 and 2. Clearly, for this case, m , m , and f Km f K just in two iterations, with an accuracy of 99.8%. To validate the present scheme for real measurements, the instantaneous streamwise velocity =U1 + u1 is obtained using hot-wire anemometry along the centerline of a twodimensional plane jet issuing from a rectangular w h = 340 5.6 mm2 slot, with aspect ratio w / h = 60. Here only a brief description of the jet facility is given as details may be found in 11 . To ensure statistical two-dimensionality, two parallel plates 2000 1800 mm2 are attached to the short sides of the slot so that the jet mixes with ambient uid only in the direction normal to the long sides, following, e.g., Gutmark and Wygnanski 12 . The jet exit velocity is U j 8 m / s, which corresponds to a Reynolds number Re U jh / of approximately 3000. Velocity measurements are performed over the region 20 x1 / h 160 using a single hot-wire tungsten probe.

The hot-wire sensor is 5 m in diameter and approximately 0.8 mm in length, aligned in the spanwise x3 direction. Velocity signals obtained at all the measured locations are lowpass ltered with a high and identical cutoff frequency of f c = 9.2 kHz. Then they are digitized at f s = 2f c = 18.4 kHz via a 16-channel, 12-bit analog-to-digital converter on a personal computer. The sampling duration is approximately 22 s. The wire calibration is conducted using a standard pitot tube in the jet potential core near to the exit where u21/2 / U j 0.5%. 1 The above measurements yield the original velocity sig0 0 0 nals U1m t = U1m + u1m t , which are corrected for the hotwire length of 0.8 mm using Wyngaards approach 13 , and, consequently, the original time derivatives along the jet centreline at x1 / h 20 are obtained as follows:
0 u1m/ t 0 0 1 0 u1m/ t = f s u1m t + f s u1m t

with

1 t = fs .

18
0 In this region, the original mean velocity U1m not presented is found to follow closely the relation Uc / U j x1 / h 1/2 here Uc denotes the centreline mean velocity , which is required by self-preservation of the jet. This relation and also that for the half-velocity width, i.e., L1/2 / h x1 / h, are well satised by previous data e.g., 4 obtained in the far eld. For high-Re ows, it is usually considered that the dissipation of turbulent kinetic energy out of the smallest-scale structures is equal to the supply rate of the turbulence energy from the large-scale structures, which is of order U3 / L0, 0 where U0 and L0 are the local characteristic velocity and length scales see, e.g., 14 . Based on this argument, we obtain U3 / L1/2, by taking U0 = Uc and L0 = L1/2, for a c plane jet. It follows that self-preservation of the ow further requires

TABLE I. Use of the iterative scheme for f c = 10f K. Iterations i 0 1 2

i i m i m i

fc

f Km 2.0f K 1.02f K 1.002f K

10f K 2.0f K 1.02f K

17.0 1.10 1.02

0.5 0.98 0.998

hU3 = C x1/h j and

5/2

19

066304-3

MI, DEO, AND NATHAN

PHYSICAL REVIEW E 71, 066304 2005

FIG. 3. Color online Centerline variations of h1 for the plane jet. m

hU3 and j

/h = C x1/h

5/8

20

where C and C are constants determined by experiments. Indeed, both Eqs. 19 and 20 have been veried by Antonia et al. 4 who found that C 1.3 and C 0.94 Re3/4. j These relations provide a rigorous basis against which to validate the proposed iterative ltering scheme using our jet 0 0 0 centerline velocity signal U1m t = U1m + u1m t for x1 / h 20. Figure 3 presents the results of m and m calculated from the original signal and after three iterations of digital lteri ing. The iterative procedure is involved in obtaining m from i i 5 via 18 and m and f Km from 1 and 6 . As with the example presented earlier, it is found that only three iterai i i tions N = 3 are required for m , m , and f Km at all measured locations to converge to their asymptotic values when setting = 103 note that a smaller value of requires more iterations; e.g., N = 5 if = 104 . Also shown in Fig. 3 are Eqs. 19 and 20 using C 1.3 and C 0.94 Re3/4 obtained j by Antonia et al. 4 . 3 3 Figure 3 demonstrates that the data of m and m agree almost identically with the curves of Eqs. 19 and 20 throughout the measured region. This provides strong support both for the validity of the iterative scheme and for the values C 1.3 and C 0.94 Re3/4. It is also noted that, j 0 0 while m lies well above Eq. 20 , m falls below Eq. 19 . As x1 increases, f K decreases and thus the ratio f c0 / f K increases so that the relative contribution of electronic noise 0 0 grows rapidly. Consequently, m and m show increased departures from their true values with increased x1. This problem may be responsible for errors in some previously reported data, since the delicate setting for the low-pass lter

described in 4 may not work very well due to the fact that f K is unknown a priori. A typical example of data that is apparently contaminated by noise can be found in 15 see their Figs. 3 and 4 , where various velocity and scalar structure functions are reported. That these measurements are quite recent highlights the need for a more rigorous approach to obtain such data for basic research of turbulence. Figure 3 also illustrates the effect of overltering u1m t . In this case, the measured values of m and m can never agree with the relations 19 and 20 . The results presented 0 for this case are obtained from ltering all u1m t along the centerline at f c = 350 Hz, which is one-half of f K for x1 / h = 160. Interestingly, these measurements of m agree quite well with those from previous studies 12,16 , where their values of mh / U3 were converted from their reported data. j Gutmark and Wygnanski 12 and Heskestad 16 did not offer any detailed information about their lter settings. However it is quite clear that their measurements do not follow relations 19 and 20 and therefore that their signals might well be overltered. Hence, their data offered wrong information that Eq. 19 does not hold in the far eld of their jet where self-similarity of the mean ow has developed. The above observation provides further support for our iterative scheme. In summary, based on the denitions of the Kolmogorov scales and f K, a fast-convergent iterative scheme has been developed to both optimally lter the noise-contaminated hot-wire velocity signals and simultaneously nd the values of and f K. The scheme, implemented via use of the isotropy assumption and Taylors hypothesis, has been validated rmly by its application to the instantaneous velocities measured in a turbulent plane jet presented and other ows not presented here . The proposed scheme is believed to have wide signicance for basic research on ne-scale turbulence because nearly all experimental studies in this eld to date have used hot-wire measurements 17 . It has implications for past measurements, and the conclusions based on them, which may suffer to an unknown extent from the contamination of noise resulting from underltered or overltered data. Application of our scheme will allow future measurements to determine the correct cutoff frequency, as well as and f K, easily and unambiguously, so generating reliable data for better understanding of small-scale turbulence. Our scheme is much simpler and more rigorous than the previous scheme 4 and even obviates the need for analog lters, differentiators, and the like. The present scheme also applies for the measurement of temperature scalar using cold-wire anemometer for estimates of the Batchelor, instead of the Kolmogorov, scale. The support of the Australian Research Council is gratefully acknowledged.

066304-4

FAST-CONVERGENT ITERATIVE SCHEME FOR 1 N. Kolmogorov, Dokl. Akad. Nauk SSSR 30, 299 1941 Proc. R. Soc. London, Ser. A 434, 9 1991 . 2 J. O. Hinze, Turbulence, 2nd ed. McGraw-Hill, New York, 1975 , p. 218. 3 L. W. Browne, R. A. Antonia, and D. A. Shah, J. Fluid Mech. 179, 307 1987 . 4 R. A. Antonia, B. R. Satyaprakash, and A. K. M. F. Hussain, Phys. Fluids 23, 695 1980 . 5 J. Mi and G. J. Nathan, Exp. Fluids 34, 687 2003 . 6 F. H. Champagne, J. Fluid Mech. 86, 67 1978 . 7 S. Corrsin, Phys. Fluids 7, 1156 1964 . 8 Y.-H. Pao, Phys. Fluids 8, 1063 1965 . 9 S. G. Saddoughi and S. V. Veeravalli, J. Fluid Mech. 268, 333

PHYSICAL REVIEW E 71, 066304 2005 1994 . 10 L. M. Smith and W. C. Reynolds, Phys. Fluids A 3, 992 1991 . 11 R. Deo, J. Mi, and G. J. Nathan unpublished . 12 E. Gutmark and I. Wygnanski, J. Fluid Mech. 73, 465 1976 . 13 J. C. Wyngaard, J. Sci. Instrum. 1, 1105 1968 . 14 H. Tennekes and J. L. Lumley, A First Course in Turbulence MIT Press, Cambridge, 1972 . 15 E. Lvque, G. Ruiz-Chavarria, C. Baudet, and S. Ciliberto, Phys. Fluids 11, 1869 1999 . 16 G. Heskestad, J. Appl. Mech. 87, 735 1965 . 17 K. R. Sreenivasan and R. A. Antonia, Annu. Rev. Fluid Mech. 29, 435 1997 .

066304-5