Documente Academic
Documente Profesional
Documente Cultură
CH5-Frequency Response PDF
Încărcat de
Ridir ZolkefleDescriere originală:
Titlu original
Drepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
CH5-Frequency Response PDF
Încărcat de
Ridir ZolkefleDrepturi de autor:
Formate disponibile
KJM/MEC 522: ControlEngineering
FREQUENCY RESPONSE ANALYSIS Frequency response means the steady state response of the system to a sinusoidal input. In the frequency response methods, the input frequency is varied over the certain range and the resulting response is noted.
x(t) X(s)
G(s)
y(t) Y(s)
For the system shown in figure
Y (s) = G(s) X (s)
The input x(t ) is sinusoidal and is given by
x ( t ) = X sin t
The steady state response of a stable, linear, time invariant system to a sinusoidal input does not depend on the initial conditions.
Y (s) = G (s) X (s) = G (s) =
X s +2
2
b b b a a + + 1 + 2 + + n s + j s j s + s1 s + s 2 s + sn
Inverse Laplace gives
y (t ) = ae jt + a e jt + b1e s1t + + bn e bnt
the steady state response becomes y (t ) = ae jt + a e jt where constant a = G(s)
X (s + j ) s = j = XG ( j ) and 2 2j s +
2
KJM/MEC 522: ControlEngineering
a = G ( s)
X (s j ) s = j = XG ( j ) 2 2j s +
2
Since G ( j ) is a complex quantity,
G ( j ) = G ( j ) e j
where = G ( j ) = tan 1
Im G ( j ) Re G ( j )
but G ( j ) = G ( j ) e j = G ( j ) e j therefore a= X G ( j ) e j X G ( j ) e j and a = 2j 2j
Then
yss (t ) = X G ( j ) e j ( t + ) e j ( t + ) 2j
= X G ( j ) sin(t + ) = Y sin(t + )
If the system is stable, then the output y (t ) can be given by
y( t ) = Y sin( t + )
where
Im G ( j) Y = X G( j) and = G ( j) = tan 1 Re G ( j)
Note that for sinusoidal input
G ( j) =
Y ( j) = Amplitude ratio of the output sinusoid to the input sinusoid X ( j)
KJM/MEC 522: ControlEngineering
G ( j) = phase
Y( j) = Phase shift of the output sinusoid with respect to the input X( j)
-Input
output
Figure 2: Input and output sinusoidal signals.
There are three commonly used representations of sinusoidal transfer function: 1. Bode diagram or Logarithmic plot 2. Nyquist plot or polar plot 3. Log-magnitude versus phase plot
KJM/MEC 522: ControlEngineering
Bode diagrams or logarithmic plot. A sinusoidal transfer function may be represented by two separate plots, magnitude versus frequency plots and phase angle (in degrees) versus frequency. Therefore, Bode diagram consists of two graphs: Magnitude and phase angles are plotted against frequency in logarithmic scale. Standard representation of the logarithmic magnitude of G ( j) is 20 log G ( j) where the base of the logarithm is 10 and the unit is decibel (dB). The main advantage of using the Bode diagram is that multiplication of magnitudes can be converted into addition. A simple method of sketching is available based on asymptotic approximation. Basic factors G ( j) H ( j) The basic factors that very frequently occur in the arbitrary transfer function G ( j) H ( j) are: 1. Gain K 2. Integral and derivative factors ( j) m1 3. First order factors (1 + jT) m1 4. Quadratic factors 1 + 2 ( j / n ) + ( j / n ) 2 The gain K A number greater than unity has positive value in decibels, while a number smaller than unity has a negative value. The log-magnitude curve for a constant gain K is a horizontal straight line at the magnitude of 20 log K decibels. The phase angle of the K gain is zero. Integral and derivative factors ( j) m1 . The logarithmic magnitude of 1 / j in decibels is
m1
20 log
1 = 20 log dB j
KJM/MEC 522: ControlEngineering
The phase angle of 1 / j is constant and equal to 900. If the log-magnitude m 20 log dB is plotted against on logarithmic scale, it is a straight line with the slope of the line is m 20 dB/decade (or m 6 dB/octave).
( m log 10)dB = ( m20 log m 20)dB
If the transfer function contains the factor (1 / j) n or ( j) n , the log magnitude becomes,
20 log( j)
mn
= m20n log dB
KJM/MEC 522: ControlEngineering
The slopes of the log-magnitude curves are thus m 20 n dB/decade and the phase angles are equal m 90 0 n over the entire range. The magnitude curves will pass through the point ( 0dB, = 1) First-order factors (1 + jT) m1 The log magnitude of the first-order factor (1 + jT) m1 is
20 log(1 + jT) m1 = m 20 log 1 + 2 T 2 dB
For low frequencies, << 1 / T , the log magnitude may be approximated by m log 1 + 2 T 2 m20 log 1 = 0dB For high frequencies, >> 1 / T , m log 1 + 2 T 2 m20 log TdB Thus, m log T dB decreases/increases by 20 dB for every decade of . The curve is straight line with a slope of m 20 dB/decade. At = 1 / T , the log magnitude equals 0 dB. The exact phase angles of the factor (1 + j) m1 are m tan 1 T
At zero frequency the phase angles are 00. At corner frequency, the phase angles are = m45 0 . At infinity, the phase angles become m 90 0 .
KJM/MEC 522: ControlEngineering
Figure Normalized and scaled Bode plots for a. G(s) = s; b. G(s) = 1/s; c. G(s) = (s + a); d. G(s) = 1/(s + a) Quadratic factors 1 + 2 ( j / n ) + ( j / ) 2 Asymptotic frequency response curve
m1
KJM/MEC 522: ControlEngineering
2 20 log = 20 log 1 2 2 n 1 + 2 j + j n n 1
for low frequencies << n ,
+ 2 n
20 log 1 = 0dB , thus a horizontal line at 0 dB.
for >> n , the log magnitude becomes
2 dB 20 log 2 = 40 log n n
The equation for high-frequency is a straight line having slope 40 dB/decade The phase angle is
2 n = tan 1 2 1 2 n
1 1 + 2 j + n j n
2
KJM/MEC 522: ControlEngineering
Figure Bode asymptotes for normalized 2 and scaled G(s) = s 2 + 2 n s + n a. magnitude; b. phase
KJM/MEC 522: ControlEngineering
10
KJM/MEC 522: ControlEngineering
11
Figure Bode magnitude plot for G(s) =(s + 3)/[(s + 2)(s2 + 2s + 25)]: a. components; b. composite
KJM/MEC 522: ControlEngineering
12
Example: Draw the Bode diagram for the following transfer function
G (s) =
10(s + 3) s(s + 2)(s 2 + s + 2)
solution
G ( j) =
10( j + 3) j( j + 2)(( j) 2 + j + 2)
normalised
j + 1 7.5 3 G ( j) = 2 ( j) j + 1 ( j) + j + 1 2 2 2
This function are composed of the following factors
7.5, ( j) 1 ,1 + j ( j) 2 j , (1 + j ) 1 , 1 + j + 3 2 2 2
and the corner frequencies
= 3, 2, and
KJM/MEC 522: ControlEngineering
13
KJM/MEC 522: ControlEngineering
14
Phase Margin and Gain Margin
The gain crossover frequency is the frequency at which G ( j) , the magnitude of the open loop transfer function is unity. The phase margin is that amount of additional phase lag at the gain crossover frequency required to bring the system to the verge of instability. The phase margin is 180o plus the phase angle of the open loop transfer function at the gain crossover frequency
= 180 o +
The gain margin is the reciprocal of the magnitude G ( j) at the frequency at which the phase angle is 180o. Defining the phase crossover frequency , to be the frequency at which the phase angle of the open loop transfer function equals 180o gives the gain margin Kg.
Kg = 1 G ( j)
The gain margin is positive if Kg is greater than unity and negative if Kg is smaller than unity.
KJM/MEC 522: ControlEngineering
15
Figure 3: Gain margin and phase margin.
Figure 4: Stability using Bode plots
1. The phase margin m is the distance of the phase angle curve above 180o at the crossover frequency c , where the magnitude plot crosses the 0dB axis. 2. The gain margin, GM dB in decibels, is the distance of the magnitude plot below 0 dB axis at the frequency where the phase angle curve shows an angle of 180o.
KJM/MEC 522: ControlEngineering
16
Example Consider a system with loop gain function
G (s) =
0.325 s(s + 1)(0.5s + 1)
Determine: The asymptotic magnitude plot The crossover frequency The phase margin The frequency where the phase is 180o. The gain margin
Solution
KJM/MEC 522: ControlEngineering
17
Tutorial 1. Construct asymptotic Bode plots for the following transfer functions. 4 (a) (0.4s + 1)(s + 1) 8 (b) s(1.25s + 1)(s + 2) 3.125 (c) 2 s(s + 0.625s + 1.5625) 1.6 (d) (s + 0.4)(s + 0.8)(s + 1) 2. For a system with loop gain function 20 G (s) = (s + 5)(0.1s + 1)(0.025s + 1) (a) Plot the asymptotic Bode plot (b) At two convenient frequencies, 10 and 20, find the deviation of the true magnitude curve from the asymptotes, and sketch a section of this curve for use in part (c) (c) Determine the phase and gain margin 3. In figure 1, Gc = K and G = 2000 /[ s ( s + 20)(0.01s + 1)] (a) Construct the asymptote Bode plot and find the approximate deviation with the true curve for the frequency near the cross over to get a better approximation of the crossover frequency for K=1 (b) determine the phase margin for K =1 (c) How does a change of gain K affect Bode magnitude and the phase angle plots? What is the effect of reducing K by a factor m.
KJM/MEC 522: ControlEngineering
18
POLAR PLOTS or NYQUIST PLOTS The polar plot of a sinusoidal transfer function G ( j) is a plot of the magnitude of G ( j) versus the phase angle of G ( j) on polar co-ordinates as is varied from zero to infinity. Thus, the polar plot is the locus of vectors G ( j) G ( j) . The polar plot is often called the Nyquist plot. In polar plots the positive (negative) phase is measured counterclockwise (clockwise) from the real axis. An advantage in using a polar plot is that it depicts the frequency-response characteristics of a system over the entire frequency range in a single plot. The disadvantage is that the plot does not clearly indicate the contributions of each individual factor of the open-loop transfer function.
Figure 1
Integral and derivative factors ( j) m1 .
KJM/MEC 522: ControlEngineering
19
The polar plot of G ( j) = 1 j is the negative imaginary axis since
G ( j) =
1 1 1 = j = 90 0 j
the polar plot of G ( j) = j is the positive imaginary axis. First-order factors (1 + j) m1 For the sinusoidal transfer function
KJM/MEC 522: ControlEngineering
20
0.5 0.4 0.3 0.2 0.1 0 -0.1 -0.2 -0.3 -0.4 -0.5
Nyquist Diagram
Imaginary Axis
0.1
0.2
0.3
0.4
0.5 Real Axis
0.6
0.7
0.8
0.9
G ( j) =
1 1 = tan 1 T 2 2 1 + T 1+ T
If
approaches infinity, the magnitude of G ( j) approaches zero and the phase
angle approaches -900. The polar plot of this transfer function is a semicircle at the frequency is varied from zero to infinity. The centre is located at 0.5 on the real axis and the radius is equal to 0.5. To prove that the polar plot is a semicircle, define
G ( j) = X + jY where X =
1 and 1 + 2 T 2
2
Y=
2
T then we obtain 1 + 2 T 2
2
1 1 2 T 2 1 2 X + Y = 2 1 + 2 T 2 2
2
T 1 + = 2 2 2 1+ T
KJM/MEC 522: ControlEngineering
21
Quadratic factors 1 + 2 ( j / n ) + ( j / n ) n
The low and high frequency portions of the polar plot of the following transfer function are given as:
G ( j) =
1 , for > 0 1 + 2 ( / n ) + ( j / n ) 2
lim G ( j) = 10 0 and lim G ( j) = 0180 0
o
Figure : Polar plot of Figure 4: Polar plot showing the resonant peak and resonant frequency r
KJM/MEC 522: ControlEngineering
22
The polar plot of this sinusoidal transfer function starts at 10 0 and ends as 0180 0 as increases from zero to infinity. Thus, the high frequency portion of G ( j) is tangent to the negative real axis. The value of G ( j) in the frequency range of interest can be calculated directly or using Bode diagram of Matlab.
The exact shape of a polar plot depends on the value of the damping ratio , but the general shape of the plot is the same for both the underdamped case and overdamped case. For the underdamped case at = n , we have G ( j n ) = 1 /( j2 ) , and the phase
angle is -900. Therefore, it can be seen that the frequency at which the G ( j) locus intersects the imaginary axis is the undamped natural frequency n . The frequency point whose distance from the origin is maximum corresponds to the resonant frequency r . The peak value of G ( j) is obtained as the ration of the magnitude of the vector at the resonant frequency r to the magnitude of the vector at = 0 .
Transport lag The transport lag
G ( j) = e jT
can be written as
G ( j) = cos T j sin T = 1 T
Since the magnitude of G ( j) is always unity and the phase varies linearly with
, the polar plot of the transport lag is a unit circle.
KJM/MEC 522: ControlEngineering
23
KJM/MEC 522: ControlEngineering
24
Nyquist Stability Criterion If the open-loop transfer function G(s) has a P poles in the right-half of s plane, then for stability the G(s) locus, as a representative point s traces out the Nyquist path in the clockwise direction must encircle the 1+j0 point P times in counterclockwise.
Figure 2: Stability using Bode plots Phase margin. The phase margin is the amount of additional phase lag at the gain crossover frequency required to bring the system to the verge of instability. The gain crossover frequency is the frequency at which G ( j) , the magnitude of the open-loop transfer function, is unity. The phase margin is 180o plus the phase angle of the open-loop transfer function at the gain crossover frequency, or = 180o + . On the Nyquist plot, a line may be drawn from the origin to the point at which the unit circle cross the G(jw) locus. The angle from the negative real axis to this line is the phase margin. ths phase margin is positive for > 0 and negative
KJM/MEC 522: ControlEngineering
25
for < 0 . For a minimum phase system to be stable, the phase margin must be positive. Gain Margin. The gain margin is the reciprocal of the magnitude G ( j at the frequency at which the phase angle is 180o. Defining the phase crossover frequency 1 to be the frequency at the frequency at which the phase angle of the open-loop transfer function equals 180o gives the gain margin K g .
Kg = 1 G ( j1 )
KJM/MEC 522: ControlEngineering
26
KJM/MEC 522: ControlEngineering
27
Tutorial 1. Use the Nyquist criterion to determine the range of values of K for the stability of the system 8K a) G ( s ) = ( s + 1)( s 2 + 2s + 2) 4 K ( s + 1) b) G ( s) = 2 s (1 + 0.1s ) 4 K (1 + 0.1s ) c) G ( s ) = s 2 (1 + s ) d) G ( s ) =
Ke 0.8 s s +1
2. Consider a unity feedback control system with the open-loop transfer K function G ( s ) = 2 s( s + s + 4) Determine the value of the gain K such that the phase margin is 50o. What is the gain margin with this gain K. 3. Consider the unity-feedback control system whose open loop transfer function is
G( s) = as + 1 s2
Determine the value of a so that the phase margin is 45o. 4. Consider the control system shown in fig. Using Nyquist criteria determine the range of gain K for the stability of the system.
R(s) + C(s)
+ -
K ( s + 0.5)
+ -
1 s (s + 1)
2
S-ar putea să vă placă și
- R(S) C(S)Document16 paginiR(S) C(S)Ananthan SrijithÎncă nu există evaluări
- Unit Iii Frequency ResponseDocument28 paginiUnit Iii Frequency ResponseRaghu RamÎncă nu există evaluări
- Module 2 - 2Document68 paginiModule 2 - 2abcdÎncă nu există evaluări
- ELEC4410 Control System Design Revision NotesDocument10 paginiELEC4410 Control System Design Revision Notescjman404Încă nu există evaluări
- EE 312 Lecture 8Document15 paginiEE 312 Lecture 8دكتور كونوهاÎncă nu există evaluări
- Review On Robust Control For SISO SystemsDocument7 paginiReview On Robust Control For SISO Systemsrodrigo_trentiniÎncă nu există evaluări
- Mapping Between Z Plane and S PlaneDocument15 paginiMapping Between Z Plane and S Planeamanpanghal67% (3)
- Frequency ResponseDocument9 paginiFrequency ResponseAnanda RamanÎncă nu există evaluări
- Notes Tee602 Polar PlotDocument33 paginiNotes Tee602 Polar PlottansnvarmaÎncă nu există evaluări
- Lecture 9-10 - Frequency Response MethodsDocument68 paginiLecture 9-10 - Frequency Response MethodsDerrick Maatla Moadi100% (1)
- Lecture 14Document35 paginiLecture 14AhsabÎncă nu există evaluări
- Frequency Response Analysis: Sinusoidal Forcing of A First-Order ProcessDocument27 paginiFrequency Response Analysis: Sinusoidal Forcing of A First-Order ProcessAna PereiraÎncă nu există evaluări
- Bandpass SignallingDocument16 paginiBandpass SignallingNitin SahuÎncă nu există evaluări
- Gate Control QuestionsDocument4 paginiGate Control QuestionsAtanuMajiÎncă nu există evaluări
- EP 5511 - Lecture 07Document33 paginiEP 5511 - Lecture 07Solomon Tadesse AthlawÎncă nu există evaluări
- Lect 9-Frequency-Response-techniques 1Document68 paginiLect 9-Frequency-Response-techniques 1Tarik ZiadÎncă nu există evaluări
- Chapter 13Document27 paginiChapter 13vishiwizardÎncă nu există evaluări
- Part A: Digital Processing of Continuous-Time Signals Sampling of Continuous-Time SignalsDocument9 paginiPart A: Digital Processing of Continuous-Time Signals Sampling of Continuous-Time SignalsAnonymous PkeI8e84RsÎncă nu există evaluări
- 15.3.3 More Complex Transfer FunctionsDocument5 pagini15.3.3 More Complex Transfer Functionsramian10Încă nu există evaluări
- Notes Tee602 Bode PlotDocument23 paginiNotes Tee602 Bode PlottansnvarmaÎncă nu există evaluări
- Freq Resp BodePlots Part1Document28 paginiFreq Resp BodePlots Part1varasala sanjayÎncă nu există evaluări
- Frequency Response AnalysisDocument94 paginiFrequency Response AnalysisaniketÎncă nu există evaluări
- 5.0 Frequency ResponseDocument80 pagini5.0 Frequency ResponseIka PriyantiÎncă nu există evaluări
- Control Systems Formula SheetDocument12 paginiControl Systems Formula SheetliamhrÎncă nu există evaluări
- 08 Frequency Response Methods MechDocument21 pagini08 Frequency Response Methods MechMamodiÎncă nu există evaluări
- Freq ResponseDocument23 paginiFreq Responselili aboudÎncă nu există evaluări
- Automatic Control II - Frequency ResponseDocument49 paginiAutomatic Control II - Frequency Responseعبدالحميد أبوشينةÎncă nu există evaluări
- GMSKDocument17 paginiGMSKZahrah SaadÎncă nu există evaluări
- Frequency Response Analysis: Section 6Document45 paginiFrequency Response Analysis: Section 6Ahmed HassanÎncă nu există evaluări
- 5.4 Stability Margins: 5.4.1 Stability Margins in Terms of Gain Margin and Phase MarginDocument7 pagini5.4 Stability Margins: 5.4.1 Stability Margins in Terms of Gain Margin and Phase MarginDevesh JayaswalÎncă nu există evaluări
- Polar Plot and Its Analysis GATE Study Material in PDFDocument6 paginiPolar Plot and Its Analysis GATE Study Material in PDFimvuuser1Încă nu există evaluări
- EE2 SignalsComms SCEE08007 Datasheet 2014 Complete PDFDocument6 paginiEE2 SignalsComms SCEE08007 Datasheet 2014 Complete PDFErica StevensÎncă nu există evaluări
- Frequency Response: 1 Systems Subjected To A Sinusoidal InputDocument8 paginiFrequency Response: 1 Systems Subjected To A Sinusoidal InputFaizal Bin IbrahimÎncă nu există evaluări
- Stability Margins: NegativeDocument5 paginiStability Margins: NegativeTejaswi J DamerlaÎncă nu există evaluări
- An Introduction To Discrete Wavelet TransformsDocument36 paginiAn Introduction To Discrete Wavelet TransformsAtacan ÖzkanÎncă nu există evaluări
- Chapter5 Part2Document19 paginiChapter5 Part2Grant HeilemanÎncă nu există evaluări
- Polar Plot and Its Analysis - GATE Study Material in PDFDocument6 paginiPolar Plot and Its Analysis - GATE Study Material in PDFnidhi tripathiÎncă nu există evaluări
- 1 - Compensator Design Procedure - Lead - Lag - With ExamplesDocument12 pagini1 - Compensator Design Procedure - Lead - Lag - With ExamplesMadhav SÎncă nu există evaluări
- Geng4402 - Assignment 2: Question 1 - Nyquist Plot/Frequency Response PerformanceDocument9 paginiGeng4402 - Assignment 2: Question 1 - Nyquist Plot/Frequency Response PerformanceangelosoutiÎncă nu există evaluări
- Tutorial II DesignDocument4 paginiTutorial II Designgeofrey fungoÎncă nu există evaluări
- Fourier TransformDocument11 paginiFourier TransformpeekoenholicÎncă nu există evaluări
- 13 Freq Response AICDocument84 pagini13 Freq Response AICDavid BayuÎncă nu există evaluări
- Control Systems EE-475: Bode Plots Frequency Response AnalysisDocument59 paginiControl Systems EE-475: Bode Plots Frequency Response AnalysisTalha YousufÎncă nu există evaluări
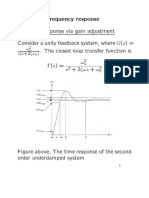
- Design via frequency response Transient response via gain adjustment Consider a unity feedback system, where G(s) = - The closed loop transfer function is T (s) = ω s + 2ζωs + ωDocument12 paginiDesign via frequency response Transient response via gain adjustment Consider a unity feedback system, where G(s) = - The closed loop transfer function is T (s) = ω s + 2ζωs + ωmdthÎncă nu există evaluări
- Chapter 6slideDocument72 paginiChapter 6slidehailegebreselassie24Încă nu există evaluări
- Control SystemsDocument18 paginiControl SystemsSengottu VelusamyÎncă nu există evaluări
- Control Systems 2Document18 paginiControl Systems 2Sengottu VelusamyÎncă nu există evaluări
- Notes Tee602 Bode Plot PDFDocument23 paginiNotes Tee602 Bode Plot PDFtansnvarmaÎncă nu există evaluări
- Digital Filters (IIR)Document28 paginiDigital Filters (IIR)Sujatanu0% (1)
- Chapter 4Document39 paginiChapter 4Joseph IbrahimÎncă nu există evaluări
- Non-Idealities of Switched Capacitor Filter DesignDocument19 paginiNon-Idealities of Switched Capacitor Filter Designhariprasath_vÎncă nu există evaluări
- Prestige Institute of Engineering & Science Indore (M.P.)Document3 paginiPrestige Institute of Engineering & Science Indore (M.P.)SagarManjrekarÎncă nu există evaluări
- Adv Contrl Tut 1Document5 paginiAdv Contrl Tut 1Anonymous LFupAa4DUÎncă nu există evaluări
- Ec1406 Control Systems Engineering 2023-2024Document38 paginiEc1406 Control Systems Engineering 2023-2024saravanan.9344308178Încă nu există evaluări
- Emcs - 607P 11-07-2014Document68 paginiEmcs - 607P 11-07-2014abdulbari.abÎncă nu există evaluări
- ConSys Compre (2017-18)Document2 paginiConSys Compre (2017-18)Dev ShahÎncă nu există evaluări
- Control System Engineering: Prof. Amitkumar B. Panchal, Assistant ProfessorDocument76 paginiControl System Engineering: Prof. Amitkumar B. Panchal, Assistant ProfessorSudhanshu Singh0% (1)
- Fundamentals of Electronics 3: Discrete-time Signals and Systems, and Quantized Level SystemsDe la EverandFundamentals of Electronics 3: Discrete-time Signals and Systems, and Quantized Level SystemsÎncă nu există evaluări
- Proportional & Integral Controllers: S K K S E S UDocument25 paginiProportional & Integral Controllers: S K K S E S UAvik GhoshÎncă nu există evaluări
- Block Diagrms ListDocument4 paginiBlock Diagrms ListRidir ZolkefleÎncă nu există evaluări
- 29 - Properties of Air and Water 61294 - 27Document30 pagini29 - Properties of Air and Water 61294 - 27Ridir ZolkefleÎncă nu există evaluări
- GMAW WeldingDocument20 paginiGMAW WeldingEdwin HarrisÎncă nu există evaluări
- Elec 436Document2 paginiElec 436Ridir ZolkefleÎncă nu există evaluări
- Descriptions of Reversed Yielding in BendingDocument21 paginiDescriptions of Reversed Yielding in BendingRidir ZolkefleÎncă nu există evaluări
- X 9Document1 paginăX 9Ridir ZolkefleÎncă nu există evaluări
- Elec 436Document2 paginiElec 436Ridir ZolkefleÎncă nu există evaluări
- OpenCV 3.0 Computer Vision With Java - Sample ChapterDocument27 paginiOpenCV 3.0 Computer Vision With Java - Sample ChapterPackt PublishingÎncă nu există evaluări
- Built in Classes in JavaDocument104 paginiBuilt in Classes in JavaarchanaÎncă nu există evaluări
- Blender 04Document38 paginiBlender 04Ana Maria100% (1)
- Document R0908A - Complete Guide To Reach OnAir! V3.0Document33 paginiDocument R0908A - Complete Guide To Reach OnAir! V3.0scribdlertooÎncă nu există evaluări
- Electrical Power Systems Wadhwa 15Document1 paginăElectrical Power Systems Wadhwa 15ragupaÎncă nu există evaluări
- Design and Analysis of Different Orders of Active-Rc Butterworth FilterDocument124 paginiDesign and Analysis of Different Orders of Active-Rc Butterworth FilterPradeep Kumar Goud NadikudaÎncă nu există evaluări
- Novel PWM Inverter Strategy For A Inverter Open End Winding Induction MotorDocument7 paginiNovel PWM Inverter Strategy For A Inverter Open End Winding Induction MotorGanesh ChallaÎncă nu există evaluări
- Lewmar Marine Equipment Guide Ed 14Document224 paginiLewmar Marine Equipment Guide Ed 14Renato Fonseca100% (1)
- Resume Executive Summary ExampleDocument5 paginiResume Executive Summary ExampleSathish GunasekarÎncă nu există evaluări
- KPODocument18 paginiKPOjohnrichardjasmineÎncă nu există evaluări
- TM - A5ck, CC, CM - y PDFDocument102 paginiTM - A5ck, CC, CM - y PDFslipargolokÎncă nu există evaluări
- SCDL - PGDBA - Finance - Sem 2 - Strategic ManagementDocument20 paginiSCDL - PGDBA - Finance - Sem 2 - Strategic Managementapi-3762419100% (2)
- Hw3 UpdatedDocument2 paginiHw3 UpdatedGeoffrey Liu0% (1)
- CE Board Nov 2020 - Hydraulics - Set 11Document1 paginăCE Board Nov 2020 - Hydraulics - Set 11Justine Ejay MoscosaÎncă nu există evaluări
- 29 Oct. To 4 Nov. 211Document16 pagini29 Oct. To 4 Nov. 211pratidinÎncă nu există evaluări
- 6141-Article Text PDF-9899-1-10-20130718 PDFDocument15 pagini6141-Article Text PDF-9899-1-10-20130718 PDFGroup-IV ADAM 2019-20Încă nu există evaluări
- CASE STUDY - Collapsed Wind Tower - A Root Cause Investigation (Element Materials Technology)Document3 paginiCASE STUDY - Collapsed Wind Tower - A Root Cause Investigation (Element Materials Technology)engrrahman3135Încă nu există evaluări
- Pressure Sensors - Nautilus: For Control Circuits, Type XML-F PresentationDocument11 paginiPressure Sensors - Nautilus: For Control Circuits, Type XML-F PresentationxzxÎncă nu există evaluări
- Drawings Phase IIDocument12 paginiDrawings Phase IIY Go GltdÎncă nu există evaluări
- Power GenerationDocument34 paginiPower GenerationTaufiq AkbarÎncă nu există evaluări
- 2020.04.24 BC thamtratonghop TKCS Trường Fulbright Lần 1Document32 pagini2020.04.24 BC thamtratonghop TKCS Trường Fulbright Lần 1Khac Hoang PhamÎncă nu există evaluări
- Drilling Data Handbook 9th EditionDocument4 paginiDrilling Data Handbook 9th Editiondedete50% (2)
- Chhattisgarh Swami Vivekanand Technical University, BhilaiDocument26 paginiChhattisgarh Swami Vivekanand Technical University, BhilaiSK BeharÎncă nu există evaluări
- English Daily ConversationDocument27 paginiEnglish Daily ConversationIrma Chyntia Dewi100% (2)
- Passport Appointment PDFDocument5 paginiPassport Appointment PDFRitu AgarwalÎncă nu există evaluări
- Electronic Let Off MotionDocument3 paginiElectronic Let Off MotionWaqar Baloch100% (2)
- Technology Architecture For NginX, postgreSQL, postgRESTDocument5 paginiTechnology Architecture For NginX, postgreSQL, postgRESTkarelvdwalt9366Încă nu există evaluări
- ERPtips SAP Training Manual SAMPLE CHAPTER From Basic PayrollDocument20 paginiERPtips SAP Training Manual SAMPLE CHAPTER From Basic Payrollravibabu1620Încă nu există evaluări
- Jobs Movie ReviewDocument2 paginiJobs Movie ReviewSaleh RehmanÎncă nu există evaluări
- Chapter 1: INTRODUCTION: 1.1 BackgroundDocument5 paginiChapter 1: INTRODUCTION: 1.1 BackgroundAhsan azizÎncă nu există evaluări