Documente Academic
Documente Profesional
Documente Cultură
Akaike 1981
Încărcat de
elfo111Descriere originală:
Drepturi de autor
Formate disponibile
Partajați acest document
Partajați sau inserați document
Vi se pare util acest document?
Este necorespunzător acest conținut?
Raportați acest documentDrepturi de autor:
Formate disponibile
Akaike 1981
Încărcat de
elfo111Drepturi de autor:
Formate disponibile
Journal
of Econometrics
16 (1981) 3-14. North-Holland
Publishing
Company
LIKELIHOOD
OF A MODEL Hirotugu
AND INFORMATION AKAIKE
CRITERIA
The Institute
ofStatisticul Muthematics. Tokyo, 106, Japan
1. Introduction Akaike (1977) introduced a principle of statistical model building, the entropy maximization principle, which regards any statistical activity as an effort to maximize the expected entropy of the resulting estimate of the distribution of a future observation. The principle is characterized by the introduction of the entropy criterion and the predictive point of view. The entropy of a distribution f (. ) with respect to another distribution g( . ) is defined by
The entropy is a natural criterion of fit of g( . ) to f (. ). The larger is the entropy the better is the approximation of f( ) by g( . ). Since the entropy can be represented in the form
B(J;g)=Elogg(x)-Elogf(x),
where E denotes the expectation with respect to the true distribution f (. ) of x, large expected log likelihood E log g(x) means large entropy. The importance of the log likelihood logg(x) stems from the fact that it is a natural estimate of Elog g(x). The basic idea underlying the use of an information criterion, called AIC, for model selection is the maximization of the expected log likelihood of a model determined by the method of maximum likelihood [Akaike (1973, 1974)]. Thus it can be viewed as a realization of the entropy maximization as the Kullback-Leibler principle. The negentropy -B (A g) is known information I (f, g). It is only by this coincidence that the criterion was called an information criterion rather than an entropy criterion. 01657410/81/0000-0000/$02.50 0 North-Holland Publishing Company
H. Akaike, Likelihood of a model and information criteria
The entropy maximization principle provides a unifying view of statistical model building. Particularly it allows the evaluation of the role of Bayesian models in statistical inference. The principle naturally suggests the necessity of the analysis of the concept of likelihood at various levels of Bayesian modeling. In this paper we start with the discussion of a paradox in the definition of the likelihood of a Bayesian model with a vague prior distribution of the parameter. Our analysis leads to the concept of the predictive likelihood of a model which solves the paradox and naturally leads to the definition of AIC as minus twice the predictive log likelihood of a model. The criteria for model selection developed by Schwarz (1978) and Sawa (1978) are discussed briefly to eliminate possible misconceptions about information criteria.
2. A paradox Model selection is a problem of statistical decision. Thus it is natural and useful to try to formulate it within the Bayesian framework. Consider the composite Bayesian model which is composed of the component models specified by the data distributions fk(. 1O,), prior distributions pk(dk), and prior probabilities n(k), k = 1,2,. . ., L. When data x is observed the prior distribution p,(O,)n(k) is transformed by the Bayes procedure into the posterior distribution
where pk(ek,x),h~+k)Pko
n(k,X)Jw)~(k)
f(x)
f(x)k)
and where
Here pk(& ) x) is the posterior assumption of the kth model defined by the distribution
distribution of the parameter and f(x 1k) is the likelihood
8, under the of the model
We will call f(x ( k) the likelihood
of the kth model.
H. Akaike, Likelihood of a mode/ and information criteriu
In practical applications it is sometimes diflicult to specify a prior distribution ~~(0~) completely and the concept of vague prior distribution is developed. The difficulty with this concept in the case of a model selection is that, since it avoids the explicit specification of pk(Ok), it does not allow the calculation of the likelihood f (X ) k) of the model. To illustrate the difficulty consider the set of data distributions fk(x) l&J, k = 0,1,2,. ., L, defined by
where the parameter 6, is a k-dimensional vector assumed to be known. We assume the prior k = 1,2,. . ., L, defined by
(8,,,&, . . ., 19~~) and rr2 is distributions pk(&) for
For a given x the likelihood
&(x [ k) of the kth model is given by
exp
When 6 is increased to infinity the likelihood goes down to zero, except for the model with k=O. This constitutes a paradox in the use of vague prior distributions for model selection. This difticulty is well known in the literature on Bayesian approach to model selection; see, for example, Atkinson and Cox (1974) and Atkinson (1978).
3. Incremental A suggestion the relation
likelihood for the solution of the above paradox can be obtained from
Log likelihood
= Incremental -t-Prior
log likelihood
log likelihood as the expected log likelihood under
Here the prior log likelihood
is defined
H. Akaike, Likelihood of a model and information criteria
the assumption of the model. The incremental log likelihood is the difference between the log likelihood of the model and its expected value and represents the net effect of the evidence produced by data on the likelihood of the model. In the composite Bayesian model considered in the preceding section, the prior log likelihood of the kth model is given by
Nd=.kdy) kVogS,b) k)dy.
B(k) represents our expectation of the log likelihood under the assumption of the kth model and the effect of the evidence produced by data x in support of the kth model is measured by the incremental log likelihood, the difference of logf,(x 1k) and B(k). We have -2B(k)=klog(a2+S2)+(L-k)logcr2+C, where C = L(log 2n + 1). The incremental given by likelihood of the kth model is then
= exp [
-f
g&i~x~+~j~~+lx:-L)].
If we let 6 grow to infinity trivial limit
the incremental
likelihood
converges
to a non-
Thus we can see that the incremental likelihood of a model does not cause the paradox observed in the preceding section. Incidentally we note that g, (x 1k) is proportional to the maximum likelihood of the kth model which is defined by putting Oki= xi, i = 1,2,. . ., k, in f(x IO,). One may consider the use of g, (x (k) as an approximation to g,(x ( k), but this is rather problematical. Actually g,(x) k) should be considered as an approximation to g, (x 1k) defined by replacing d2 of g,(x ) k) by s2 which is much larger than 6 of the original model. g,(x I k) is then the incremental likelihood of the model specified by the prior distribution of the parameter 61k which is normal with mean zero and variance matrix ~~1, xk. To consider such a model means that, even though we know that the original prior distribution of tIk is with mean zero and variance matrix ~3~1,we consider the
H. Akaike,
Likelihood
of a model and information
criteria
use of a model with much larger dispersion of the prior distribution the difficulty of explicitly specifying the value of 6. Now we have
to avoid
with respect to the true distribution Eyld denotes the expectation e correct this bias caused by the change of the model and MYI k) of Y. W define the incremental log likelihood of the kth model with the vague prior distribution of ok by where
4. Prior likelihoods For a finite 6 the prior log likelihood B(k)= B(k) of the kth model is given by
-(~)[klog(aZ+62)+(L-k)loga2+C].
Obviously, except for k =O, B(k) goes to minus infinity when 6 grows to infinity. This explains the nature of the paradox of the likelihood of a Bayesian model with a vague prior distribution. To solve this difficulty we must develop a deeper analysis of the likelihood of a model. The following representation of the prior log likelihood is useful for this purpose: Prior log likelihood of the kth model
where
Here we invoke the predictive point of view underlying the entropy maximization principle. When data x is observed the prior distribution pk(Bk) will be replaced by the posterior distribution p(& Ix). At this point the distribution f, (y 1k) will be replaced by the predictive distribution
If. Akaike, Likelihood of a model and information criteria
The expected log likelihood of this assumption of the kth model is given by
predictive
distribution
under
the
This expected log likelihood is a quantity defmed prior to the observation of x and we call it the prior predictive log likelihood. The use of the prior predictive log likelihoods of the component models in a composite Bayesian model, in place of the prior log likelihoods, constitutes the departing point of our approach to model selection from the conventional Bayesian approach. The definition of the prior predictive likelihood allows a natural extension to the case where the prior distribution pk(Ok) is vague. The posterior distribution ~(0, 1 of ek defined with the prior distribution x) pk.&) is normal with mean [??/(a + S)]x[k] and variance matrix [02S2/(02 + S2)]Z,, k, where x[k] denotes the vector (x,, x2,. . ., xk). The posterior distribution corresponding to the vague prior distribution of 8, is then defined by letting 6 go to infinity and is normal with mean x[k] and variance matrix 0~1, x k. For this posterior distribution we have the predictive distribution
p(y[ k,x)=(&~2(&)*:2($~-k)2
x exp
Accordingly
we get
= -(+)[Llog(2za2)+L.+klog2]. Since this quantity is independent of the value of 13~it is natural to define the prior predictive likelihood of the kth model by exp [C*(k)] or 2-k2. It should be noticed that the prior predictive likelihood can be defined if only a predictive distribution is given. A conventional use of a posterior distribution of a parameter is to use its mode as an estimate of the parameter. The mode of the posterior distribution of Ok for the vague prior distribution defined in the preceding paragraph is identical to the maximum The corresponding predictive likelihood estimate of the parameter.
H. Akaike,
Likelihood
of a model and information
criteria
distribution
is then defined by f (y If?,) with Ok=x[k].
For this case we have
C**W=~{f(x(Wf(y[
e,)Closf(Y(xCkl)ldydx
= -(+)[Llog(2r&)+L+k]. The prior predictive likelihood of the kth model for the present choice of the predictive distribution is thus defined by exp [C**(k)] or eCki2.
5. Predictive likelihood of a model If we put pk(Qk 1x)=pk(Bk) in the definition of the predictive distribution p (y 1k, x) we get p (y 1k, x) =fs (y 1k) and the prior likelihood of this predictive distribution is exactly the prior likelihood of the model specified by pk(Br). This corresponds to the extreme situation of the choice of the predictive distribution where the information supplied by the prior distribution is by far the more significant than that provided by the likelihood function fk (x IO,). If pk(Ok) is well concentrated, compared with the likelihood function fk(x ) /iI,), the posterior distribution pk (OkIx). will be a good approximation to pk(Ok) and the prior predictive likelihood provides a reasonable approximation to the prior likelihood. When the prior distribution pk(ek) is vague, all that we know is that eventually we will define some kind of predictive distribution by using the information supplied by data. Here the original definition of the prior log likelihood loses its meaning as a measure of the expected goodness of the to each individual data distribution distribution fs ( .I k) as an approximation fk( / 0,). In this case it would be more natural to shift the meaning of the prior log likelihood from the original definition to that of the prior predictive log likelihood which evaluates the expected goodness of the predictive distribution as an approximation to each individual data distribution. These observations suggest that the prior predictive likelihood is a natural extension of the prior likelihood of a model. A natural definition of the likelihood of a predictive distribution is then given by Log likelihood = Prior predictive + Incremental log likelihood log likelihood.
Although the likelihood defined by the above equality is the likelihood of the predictive distribution, we will simply call it the predictive likelihood of the model. Obviously the definition depends on the choice of the predictive distribution. We arrived at the same definition of the predictive likelihood of a model in Akaike (1978b, c) by a slightly different reasoning. The derivation
10
H. Akaike,
Likelihood
of a model and information criteria
developed in this paper provides a better explanation of its relation to the Bayesian modeling. Our main proposal in this paper is to use the predictive likelihoods in place of the original likelihoods of the component models of a composite Bayesian model. In the case of a component Bayesian model defined with a proper prior distribution this means a modification of the prior probability by multiplying it with a factor proportional to the ratio of the prior predictive likelihood to the prior likelihood. This modification of the prior probability may be viewed as the change of our preference of the model caused by the shifting of our attention from I)~(&) to ~~(0~ 1x). With this shift of the viewing position and with the aid of the definition of the incremental likelihood we can develop a fairly systematic procedure of handling vague prior distributions.
6. Maximum
predictive likelihood
selection procedure and AIC
For the composite Bayesian models, discussed in the proceding sections, if the predictive distributions are defined by the models with the parameters determined by the method of maximum likelihood, the predictive likelihoods are given by 4(x( k)=h(x = exp
1 k)exp (-Sk)
xf
Thus we have the relation (- 2) log q (x 1k) = (- 2) log maximum
likelihood
of the model f(x18,)+2k*+c,
where k* denotes the dimension of 8, which is now identical to k and c denotes a constant independent of k. This last quantity is equivalent to an information criterion (AIC) introduced by the present author for the comparison of models with parameters determined by the method of maximum likelihood [Akaike (1973, 1974)]. Thus the minimum AIC procedure which selects the model with the minimum value of AIC is now viewed as the maximum predictive likelihood selection procedure.
H. Akaike,
Likelihood
of a
model and information
criteria
11
7.
Schwa&s
criterion (1978) proposed a selection procedure which minimizes the
Schwarz criterion
( - 2) log maximum
likelihood
+ log N (number
of parameters),
where N is the number of independently repeated observations. In the case of the model considered in this paper, we may envisage the situation by putting 0 = az/N, where gg is a constant, and xi =Xi, the sample mean of N observations. The criterion is obtained by analyzing the behavior of the posterior probability of the kth model when N grows to infinity under the assumption of some proper prior distributions of the parameters. For any finite and fixed N the procedure formally reduces to the maximum predictive likelihood selection procedure with the predictive likelihoods defined by the products of the incremental likelihoods h(x 1k) and the prior likelihoods (N/e)- k2. Consider the two situations where c2 = cr:lN, =0:/N, defined with different values N, and N, of N. Even though the likelihoods of Ok behave similarly for the two situations, the prior likelihoods are significantly influenced by the knowledge of N. Thus the criterion is not an information criterion which is based on the expected behavior of the log likelihood of 0,. The use of this type of procedure is possible only under the strong conviction of the assumed prior distributions of the parameters. This is possible only when we have clearly defined proper prior distributions, a situation where straightforward application of the Bayes procedure is all that is necessary to solve the problem of model selection. This observation shows that the use of Schwarzs procedure in a practical situation will be problematical. Stone (1979) developed a comparative study of Schwarzs criterion and AIC. He also questions the realism of asymptotic investigations under the assumption of a fixed model. Schwarz did not develop any characterization of his procedure for finite N. For the composite model treated in this paper we actually have N = 1 with 0 = O& and there is no hope of getting meaningful result by the procedure. This shows that anyone who wants to use the procedure must develop his own justification for each particular application. Similar consideration is necessary for the application of the criterion of Hannan and Quinn (1979) for the selection of the order of an autoregression.
8. Sawas criterion Sawa (1978) developed a critical analysis of AIC. AIC was originally defined as an estimate of minus twice the expected log likelihood of the model specified by the parameters determined by the method of maximum
12
H. Akaike, Likelihood
of a model
and information criteria
likelihood. Sawa considers that the assumption underlying the derivation of AIC is unsatisfactory. The criterion is derived under the assumption that the deviation of the best approximating model from the true distribution is of comparable order to the sampling variability of the estimated model, as measured in terms of the expected log likelihood. Sawa introduced a criterion for the selection of regression models which was supposed to be free from this assumption. This correction of AIC was further pursued and generalized by Chow (1979). Earlier Takeuchi (1976) proposed similar correction. These corrections were introduced based on some analyses of the characteristics of the maximum likelihood estimates under non-standard conditions. Unfortunately the corrections do not seem quite successful. This is due to the fact that they require either some additional assumptions or ad hoc estimates of the necessary quantities. This makes unclear the practical advantage of these corrected estimates over the original ATC. The implication of the minimum AIC procedure for model selection is that, if a researcher feels definite uncertainty about the choice of his models, he should try to explicitly represent it by introducing new models, rather than to apply a refined criterion to the original models. The analysis of the present paper also suggests the possibility of developing other corrections by modifying the structure of the assumed prior distribution of the parameter. Although this is not concerned with the correction of AIC one such example is given by Akaike (1978a) in developing the proof of a minimax type optimality of the minimum AIC procedure. Another example is seen in a paper by Smith and Spiegelhalter (1980). A typical Bayesian reaction to information criteria can be found in the comment on Sawas paper by Learner (1979). Learner dispenses with the inferential aspect by saying that solutions to the inference problem are well known through Bayesian modeling. However, as our present analysis has shown, the main problem of inference lies in the choice of the prior probabilities of the component models. Information criteria are implicitly producing practical solutions to this problem.
9. Information
criteria and Bayesian modeling
In a practical situation of model selection it is desirable to develop a proper Bayesian modeling as far as possible. Nevertheless we often come to the stage where we must accept the vagueness of the prior distributions of some parameters or hyperparameters. When these parameters have different dimensionalities in different models a criterion like AIC is required to realize a selection procedure. As was noticed in the discussion of predictive likelihood the choice of a particular prior predictive likelihood may be viewed as a way of defining a
H. Akaike, Likelihood of a model and information criteria
13
prior probability of the model within the Bayesian framework. This does not contain any problem from the Bayesian point of view. In the case of the model treated in this paper the problem lies in the process of replacing the incremental likelihood g,(x 1k) by h(x 1k) w h en the prior distribution of the parameter is vague. This replacement means to adopt k as an approximation of the term
in the definition of the incremental log likelihood. Under the assumption of the kth model this quantity is distributed chi-square variable with the degrees of freedom k. The expected error approximation increases with k. Since the incremental likelihoods h(x introduced as approximations to g, (x 1k), this fact must be reflected choice of the prior probabilities of the models. One may consider the the prior probabilities defined by the relation n(k)cc exp (-yk). With this choice of the prior probability model is defined by the relation log (posterior =Predictive probability the posterior probability
as a of this ) k) are in our use of
of the kth
of the kth model) of the kth modelyk.
log likelihood
By a proper choice of y the penalty for the error in the approximation of the incremental likelihood will find a reasonable representation at least for a small group of neighboring values of k. The main problem here is the choice of y. This problem has been discussed in relation to the application of AIC to the autoregressive model fitting [Akaike (1978b, 1979)]. There exp (-0.5 AIC) is used as the definition of the likelihood of a model specified by the maximum likelihood estimate of the parameter. Further extension of the procedure to all subset regression analysis type problem is discussed in Akaike (1978~). These results are extensively used in the program package TIMSACfor time series analysis and control [Akaike, Kitagawa, Arahata and Tada (1979)].
Akaike, H., 1973, Information theory and an extension of the maximum B.N. Petrov and F. Csaki, eds., 2nd international symposium (Akademiai Kiado, Budapest).
likelihood principle, in: on information theory
14
H. Akaike, Likelihood of a model and information criteria
Akaike, H., 1974, A new look at the statistical model identification, IEEE Transactions on Automatic Control AC-19, 716-723. Akaike. H., 1977, On entropy maximization principle, in: P.R. Krishnaiah ed., Applications of statistics (North-Holland: Amsterdam). Akaike, H., 1978a, A Bayesian analysis of the minimum AIC procedure, Annals of the Institute of Statistical Mathematics 30, A, 9-14. Akaike, H., 1978b, On the likelihood of a time series model, The Statistician 27, 217-235. Akaike. H.. 1978~. Likelihood of a model. Research memorandum no. 127 (The Institute of Staiistical Mathematics, Tokyo). Akaike, H., 1979, A Bayesian extension of the minimum AIC procedure of autoregressive model fitting, Biometrika 66, 237-242. Akaike, H., G. Kitagawa, E. Arahata and F. Tada, 1979, TIMSAC-78, Computer Science Monographs no. 11 (The Institute of Statistical Mathematics, Tokyo). Atkinson, AC., 1978, Posterior probabilities for choosing a regression model, Biometrika 65, 3948. Atkinson, A.C. and D.R. Cox, 1974, Planning experiments for discriminating between models (with discussion), Journal of the Royal Statistical Society B36, 321-348. Chow, G.C., 1979, Selection of econometric models by the information criterion, Economic Research Program research memorandum no. 239 (Econometric Research Program, Princeton University, Princeton, NJ). Hannan, E.J. and B.G. Quinn, 1979, The determination of the order of an autoregression, Journal of the Royal Statistical Society B41, 190-195. Learner, E.E., 1979, Information criteria for choice of regression models: A comment, Econometrica 47, 507-510. Sawa, T., 1978, Information criteria for discriminating among alternative regression models, Econometrica 46, 1273-1291. Stone. M.. 1979. Comments on model selection criteria of Akaike and Schwarz, Journal of the Royal &ati&al Society B41, 276-278. Schwarz, G., 1978, Estimating the dimension of a model, Annals of Statistics 6, 461464. Smith, A.F.M. and D.J. Spiegelhalter, 1980, Bayes factors and choice criteria for linear models, Journal of the Royal Statistical Society B42, 213-220. Takeuchi, K., 1976, The distribution of information statistic and the criterion of the adequacy of a model, Suri-Kagaku (Mathematical Sciences), no. 3, 12-18 (in Japanese).
S-ar putea să vă placă și
- Mathematical Foundations of Information TheoryDe la EverandMathematical Foundations of Information TheoryEvaluare: 3.5 din 5 stele3.5/5 (9)
- Marginal Likelihood Estimation Via Power Posteriors: N. FrielDocument13 paginiMarginal Likelihood Estimation Via Power Posteriors: N. FrielsssÎncă nu există evaluări
- Digital Signal Processing (DSP) with Python ProgrammingDe la EverandDigital Signal Processing (DSP) with Python ProgrammingÎncă nu există evaluări
- Hist PDFDocument17 paginiHist PDFrushitaaÎncă nu există evaluări
- Machine Learning and Pattern Recognition Week 3 Intro - ClassificationDocument5 paginiMachine Learning and Pattern Recognition Week 3 Intro - ClassificationzeliawillscumbergÎncă nu există evaluări
- Chap 4Document21 paginiChap 4ehsan_civil_62Încă nu există evaluări
- Mixed Model Selection Information TheoreticDocument7 paginiMixed Model Selection Information TheoreticJesse Albert CancholaÎncă nu există evaluări
- Bayesian Monte Carlo: Carl Edward Rasmussen and Zoubin GhahramaniDocument8 paginiBayesian Monte Carlo: Carl Edward Rasmussen and Zoubin GhahramanifishelderÎncă nu există evaluări
- Digital Communication NotesDocument9 paginiDigital Communication NotesSABHASACHI POBIÎncă nu există evaluări
- CHP 1curve FittingDocument21 paginiCHP 1curve FittingAbrar HashmiÎncă nu există evaluări
- Markov Chain Order Estimation and The Chi-Square DivergenceDocument19 paginiMarkov Chain Order Estimation and The Chi-Square DivergenceYXZ300Încă nu există evaluări
- Comparison of Resampling Method Applied To Censored DataDocument8 paginiComparison of Resampling Method Applied To Censored DataIlya KorsunskyÎncă nu există evaluări
- Gap PDFDocument13 paginiGap PDFAdeliton DelkÎncă nu există evaluări
- Guessing Probability Distributions From Small Samples: Obs K K ObsDocument10 paginiGuessing Probability Distributions From Small Samples: Obs K K Obsibrahim1Încă nu există evaluări
- Theory For Penalised Spline Regression: Peter - Hall@anu - Edu.auDocument14 paginiTheory For Penalised Spline Regression: Peter - Hall@anu - Edu.auAnn FeeÎncă nu există evaluări
- Breidt Claeskens Opsomer 2005Document31 paginiBreidt Claeskens Opsomer 2005RaulÎncă nu există evaluări
- Negative Spherical PerceptronDocument14 paginiNegative Spherical Perceptroncrocoali000Încă nu există evaluări
- Kernal Methods Machine LearningDocument53 paginiKernal Methods Machine LearningpalaniÎncă nu există evaluări
- General Least Squares Smoothing and Differentiation of Nonuniformly Spaced Data by The Convolution Method.Document3 paginiGeneral Least Squares Smoothing and Differentiation of Nonuniformly Spaced Data by The Convolution Method.Vladimir PelekhatyÎncă nu există evaluări
- Research PaperDocument10 paginiResearch PaperAaron StewartÎncă nu există evaluări
- 10.3934 Amc.2021067Document25 pagini10.3934 Amc.2021067Reza DastbastehÎncă nu există evaluări
- Particlefilter EqualizationDocument4 paginiParticlefilter Equalizationnguyentai325Încă nu există evaluări
- Engineering Statistics - 4Document43 paginiEngineering Statistics - 4Kader KARAAĞAÇÎncă nu există evaluări
- Chap 2Document28 paginiChap 2Abdoul Quang CuongÎncă nu există evaluări
- Line of Sight Rate Estimation With PFDocument5 paginiLine of Sight Rate Estimation With PFAlpaslan KocaÎncă nu există evaluări
- A Ballistic Monte Carlo Approximation of πDocument4 paginiA Ballistic Monte Carlo Approximation of πWink ElliottÎncă nu există evaluări
- Factoring With Cyclotomic Polynomials : by Eric Bach and Jeffrey ShallitDocument19 paginiFactoring With Cyclotomic Polynomials : by Eric Bach and Jeffrey Shallitoctavinavarro8236Încă nu există evaluări
- NIPS 2000 The Kernel Trick For Distances PaperDocument7 paginiNIPS 2000 The Kernel Trick For Distances PaperstiananfinsenÎncă nu există evaluări
- 978-1-6654-7661-4/22/$31.00 ©2022 Ieee 1Document12 pagini978-1-6654-7661-4/22/$31.00 ©2022 Ieee 1vnodataÎncă nu există evaluări
- MCMC OriginalDocument6 paginiMCMC OriginalAleksey OrlovÎncă nu există evaluări
- Mathematics 05 00005 PDFDocument17 paginiMathematics 05 00005 PDFTaher JelleliÎncă nu există evaluări
- Kriging - Method and ApplicationDocument17 paginiKriging - Method and ApplicationanggitaÎncă nu există evaluări
- Global Convergence of A Trust-Region Sqp-Filter Algorithm For General Nonlinear ProgrammingDocument25 paginiGlobal Convergence of A Trust-Region Sqp-Filter Algorithm For General Nonlinear ProgrammingAndressa PereiraÎncă nu există evaluări
- A Truncated Nonmonotone Gauss-Newton Method For Large-Scale Nonlinear Least-Squares ProblemsDocument16 paginiA Truncated Nonmonotone Gauss-Newton Method For Large-Scale Nonlinear Least-Squares ProblemsMárcioBarbozaÎncă nu există evaluări
- An Adjusted Boxplot For SkewedDocument8 paginiAn Adjusted Boxplot For SkewedrebbolegiÎncă nu există evaluări
- Wa0193.Document4 paginiWa0193.jagarapuyajnasriÎncă nu există evaluări
- Deviance Information Criterion (DIC)Document1 paginăDeviance Information Criterion (DIC)muralidharanÎncă nu există evaluări
- Mathematical Aspects of Impedance Imaging: of Only One orDocument4 paginiMathematical Aspects of Impedance Imaging: of Only One orRevanth VennuÎncă nu există evaluări
- cdd4 PDFDocument75 paginicdd4 PDFUsman HamIdÎncă nu există evaluări
- Determining The Number of Clusters in A Data SetDocument6 paginiDetermining The Number of Clusters in A Data Setjohn949Încă nu există evaluări
- A Survey of Dimension Reduction TechniquesDocument18 paginiA Survey of Dimension Reduction TechniquesEulalio Colubio Jr.Încă nu există evaluări
- Steven L. Mielke Et Al - Extrapolation and Perturbation Schemes For Accelerating The Convergence of Quantum Mechanical Free Energy Calculations Via The Fourier Path-Integral Monte Carlo MethodDocument25 paginiSteven L. Mielke Et Al - Extrapolation and Perturbation Schemes For Accelerating The Convergence of Quantum Mechanical Free Energy Calculations Via The Fourier Path-Integral Monte Carlo MethodWippetsxzÎncă nu există evaluări
- Continuation Ratio LogitDocument13 paginiContinuation Ratio LogitamrulÎncă nu există evaluări
- Classifier Conditional Posterior Probabilities: Robert P.W. Duin, David M.J. TaxDocument9 paginiClassifier Conditional Posterior Probabilities: Robert P.W. Duin, David M.J. Taxtidjani86Încă nu există evaluări
- Advances On The Continued Fractions Method Using Better Estimations of Positive Root BoundsDocument6 paginiAdvances On The Continued Fractions Method Using Better Estimations of Positive Root Boundsnitish102Încă nu există evaluări
- Pareto Analysis TechniqueDocument15 paginiPareto Analysis TechniqueAlberipaÎncă nu există evaluări
- E$cient Estimation of Binary Choice ModelsDocument17 paginiE$cient Estimation of Binary Choice ModelsMOHAMMED DEMMUÎncă nu există evaluări
- Autocovariance Least Square Method For Estimating Noise CovariancesDocument6 paginiAutocovariance Least Square Method For Estimating Noise Covariancesnadamau22633Încă nu există evaluări
- At Salak Is 2009Document2 paginiAt Salak Is 2009ymt1123Încă nu există evaluări
- Foundations Computational Mathematics: Online Learning AlgorithmsDocument26 paginiFoundations Computational Mathematics: Online Learning AlgorithmsYuan YaoÎncă nu există evaluări
- Kernel Methods in Machine LearningDocument50 paginiKernel Methods in Machine Learningvennela gudimellaÎncă nu există evaluări
- What Is A Martingale - DoobDocument14 paginiWhat Is A Martingale - DoobSayak KolayÎncă nu există evaluări
- Cox MixturesDocument13 paginiCox MixturesRiccardo Meine ScaramuzzaÎncă nu există evaluări
- Estimating The Support of A High-Dimensional DistributionDocument28 paginiEstimating The Support of A High-Dimensional DistributionAndrés López GibsonÎncă nu există evaluări
- Kmenta Ridge RegressionDocument7 paginiKmenta Ridge RegressionTiberiu TincaÎncă nu există evaluări
- Mean Shift ClusterDocument10 paginiMean Shift ClusterSoumyajit JagdevÎncă nu există evaluări
- A Predictive Approach To The Random Effect ModelDocument7 paginiA Predictive Approach To The Random Effect ModelKamal DemmamiÎncă nu există evaluări
- On The Nystr Om Method For Approximating A Gram Matrix For Improved Kernel-Based LearningDocument23 paginiOn The Nystr Om Method For Approximating A Gram Matrix For Improved Kernel-Based LearningJhony Sandoval JuarezÎncă nu există evaluări
- David Naccache, Nigel P. Smart, and Jacques SternDocument11 paginiDavid Naccache, Nigel P. Smart, and Jacques Sternjoaozinho maneirinhoÎncă nu există evaluări
- Costos de La Tarifa 2: Periodo PeriodoDocument22 paginiCostos de La Tarifa 2: Periodo PeriodoJesús Valdez RÎncă nu există evaluări
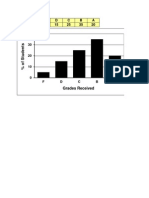
- F D C B A 5 15 25 35 20: Grades ReceivedDocument2 paginiF D C B A 5 15 25 35 20: Grades ReceivedJesús Valdez RÎncă nu există evaluări
- Available Fault Current Selective Coordination SpreadsheetDocument20 paginiAvailable Fault Current Selective Coordination SpreadsheetOmer SyedÎncă nu există evaluări
- Ansi c84.1 Voltage Level and RangeDocument6 paginiAnsi c84.1 Voltage Level and RangeJesús Valdez RÎncă nu există evaluări
- 100M Offers Made Easy: Create Your Own Irresistible Offers by Turning ChatGPT into Alex HormoziDe la Everand100M Offers Made Easy: Create Your Own Irresistible Offers by Turning ChatGPT into Alex HormoziÎncă nu există evaluări
- ChatGPT Side Hustles 2024 - Unlock the Digital Goldmine and Get AI Working for You Fast with More Than 85 Side Hustle Ideas to Boost Passive Income, Create New Cash Flow, and Get Ahead of the CurveDe la EverandChatGPT Side Hustles 2024 - Unlock the Digital Goldmine and Get AI Working for You Fast with More Than 85 Side Hustle Ideas to Boost Passive Income, Create New Cash Flow, and Get Ahead of the CurveÎncă nu există evaluări
- Generative AI: The Insights You Need from Harvard Business ReviewDe la EverandGenerative AI: The Insights You Need from Harvard Business ReviewEvaluare: 4.5 din 5 stele4.5/5 (2)
- Scary Smart: The Future of Artificial Intelligence and How You Can Save Our WorldDe la EverandScary Smart: The Future of Artificial Intelligence and How You Can Save Our WorldEvaluare: 4.5 din 5 stele4.5/5 (55)
- HBR's 10 Must Reads on AI, Analytics, and the New Machine AgeDe la EverandHBR's 10 Must Reads on AI, Analytics, and the New Machine AgeEvaluare: 4.5 din 5 stele4.5/5 (69)
- ChatGPT Money Machine 2024 - The Ultimate Chatbot Cheat Sheet to Go From Clueless Noob to Prompt Prodigy Fast! Complete AI Beginner’s Course to Catch the GPT Gold Rush Before It Leaves You BehindDe la EverandChatGPT Money Machine 2024 - The Ultimate Chatbot Cheat Sheet to Go From Clueless Noob to Prompt Prodigy Fast! Complete AI Beginner’s Course to Catch the GPT Gold Rush Before It Leaves You BehindÎncă nu există evaluări
- Mastering Large Language Models: Advanced techniques, applications, cutting-edge methods, and top LLMs (English Edition)De la EverandMastering Large Language Models: Advanced techniques, applications, cutting-edge methods, and top LLMs (English Edition)Încă nu există evaluări
- Four Battlegrounds: Power in the Age of Artificial IntelligenceDe la EverandFour Battlegrounds: Power in the Age of Artificial IntelligenceEvaluare: 5 din 5 stele5/5 (5)
- The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our WorldDe la EverandThe Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our WorldEvaluare: 4.5 din 5 stele4.5/5 (107)
- Artificial Intelligence: The Insights You Need from Harvard Business ReviewDe la EverandArtificial Intelligence: The Insights You Need from Harvard Business ReviewEvaluare: 4.5 din 5 stele4.5/5 (104)
- Working with AI: Real Stories of Human-Machine Collaboration (Management on the Cutting Edge)De la EverandWorking with AI: Real Stories of Human-Machine Collaboration (Management on the Cutting Edge)Evaluare: 5 din 5 stele5/5 (5)
- ChatGPT Millionaire 2024 - Bot-Driven Side Hustles, Prompt Engineering Shortcut Secrets, and Automated Income Streams that Print Money While You Sleep. The Ultimate Beginner’s Guide for AI BusinessDe la EverandChatGPT Millionaire 2024 - Bot-Driven Side Hustles, Prompt Engineering Shortcut Secrets, and Automated Income Streams that Print Money While You Sleep. The Ultimate Beginner’s Guide for AI BusinessÎncă nu există evaluări
- Who's Afraid of AI?: Fear and Promise in the Age of Thinking MachinesDe la EverandWho's Afraid of AI?: Fear and Promise in the Age of Thinking MachinesEvaluare: 4.5 din 5 stele4.5/5 (13)
- Artificial Intelligence: A Guide for Thinking HumansDe la EverandArtificial Intelligence: A Guide for Thinking HumansEvaluare: 4.5 din 5 stele4.5/5 (30)
- Python Machine Learning - Third Edition: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow 2, 3rd EditionDe la EverandPython Machine Learning - Third Edition: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow 2, 3rd EditionEvaluare: 5 din 5 stele5/5 (2)
- Your AI Survival Guide: Scraped Knees, Bruised Elbows, and Lessons Learned from Real-World AI DeploymentsDe la EverandYour AI Survival Guide: Scraped Knees, Bruised Elbows, and Lessons Learned from Real-World AI DeploymentsÎncă nu există evaluări
- Make Money with ChatGPT: Your Guide to Making Passive Income Online with Ease using AI: AI Wealth MasteryDe la EverandMake Money with ChatGPT: Your Guide to Making Passive Income Online with Ease using AI: AI Wealth MasteryÎncă nu există evaluări
- A Brief History of Artificial Intelligence: What It Is, Where We Are, and Where We Are GoingDe la EverandA Brief History of Artificial Intelligence: What It Is, Where We Are, and Where We Are GoingEvaluare: 4.5 din 5 stele4.5/5 (3)
- T-Minus AI: Humanity's Countdown to Artificial Intelligence and the New Pursuit of Global PowerDe la EverandT-Minus AI: Humanity's Countdown to Artificial Intelligence and the New Pursuit of Global PowerEvaluare: 4 din 5 stele4/5 (4)
- The AI Advantage: How to Put the Artificial Intelligence Revolution to WorkDe la EverandThe AI Advantage: How to Put the Artificial Intelligence Revolution to WorkEvaluare: 4 din 5 stele4/5 (7)
- The Roadmap to AI Mastery: A Guide to Building and Scaling ProjectsDe la EverandThe Roadmap to AI Mastery: A Guide to Building and Scaling ProjectsÎncă nu există evaluări
- Hands-On System Design: Learn System Design, Scaling Applications, Software Development Design Patterns with Real Use-CasesDe la EverandHands-On System Design: Learn System Design, Scaling Applications, Software Development Design Patterns with Real Use-CasesÎncă nu există evaluări
- System Design Interview: 300 Questions And Answers: Prepare And PassDe la EverandSystem Design Interview: 300 Questions And Answers: Prepare And PassÎncă nu există evaluări
- Architects of Intelligence: The truth about AI from the people building itDe la EverandArchitects of Intelligence: The truth about AI from the people building itEvaluare: 4.5 din 5 stele4.5/5 (21)