Seismic Analysis of Structures - II

T.K.
Datta
Department Of Civil Engineering, IIT Delhi Response Analysis for specified ground motion

Chapters 3 & 4

Chapter -3
RESPONSE ANALYSIS
FOR
SPECIFIED GROUND MOTION
1
T.K. Datta
Introduction
Time history analysis of structuures is carried out
when input is in the form of specified time history of
ground motion.
Time history analysis can be performed using direct
integration methods or using fourier transform
techniques.
In the direct integration methods, there are many
integration schemes; two most popular methods used
in earthquake engineering will be discussed here.
In addition, time history analysis using FFT will be
presented.
Before they are described, several concepts used
in dynamic analysis of structures under support
motion will be summerised ( assuming that they are
already known to the students).

1/1
T.K. Datta
1/2
Models for an SDOF
Spring-mass-dashpot system
Fig: 3.1 a
k

c

x

m

g
x
..
Idealized single frame
Fig: 3.1b
Rigid beam
Lumped mass
All members
are inextensible

g
x

g
x
.. ..
T.K. Datta
Equation of motion of an SDOF system can be
written in three different ways:

For MDOF system, equations of motion are written
for two cases; single & multi support excitations.

Contd..

(
` `
(
)
)
g
t t t
g g
g
t t
mx + cx + kx = -mx (3.1)
mx + cx + kx = cx + kx (3.3)
X = AX+f (3.4a)
0
x 0 1
X= A = f = (3.4b
-x
x -k/m -c/m
X = AX + Ff (3.5a)
in which
(3.5 ) b

(
` `
(

) )
t
g
t
t
g
x
0 0
x
X = ; F = ; f =
x
k/m c/m
x
1/3
T.K. Datta
For single support single component excitation

For two component ground motion

For three component ground motion

Contd..
{ }
(
(

T
T
g g1 g2
1 0 1 0 - - - - - -
I = (3.9a)
0 1 0 1 - - - - - -
X = x x (3.10a)
{ }
(
(
(
(

T
T
g g1 g2 g3
1 0 0 1 0 0 - - - -
I = 0 1 0 0 1 0 - - - - (3.9b)
0 0 1 0 0 1 - - - -
X = x x x (3.10b)
1/4
g
MX + CX + KX = -MIX (3.8)
T.K. Datta
Contd..
Example 3.1: Determine for the following structures .
Solution :

I
( (
( (

1 1 2 3 1 2 3 T T
u v u u u u u
I = I =
1 0 1 1 1 1 1
Bracket frame

3
u

2
u

1
u

Shear building frame
u
2
u
3
u
1
v
1
g
x
g
x
Fig3.4a
Fig3.4b
1/5
T.K. Datta
| |
(
=
=
0 1 0 0 1 0
0 0 1 0 0 1
0 0 1 0 0 1
T
T
I
I
Contd..

Case 1 Single component

Case 2 Two component

1 1
& v u

u
2

u
1
v
2
u
2
v
1
u
1
3-D model of a shear building frame
Fig3.4c
1/6
T.K. Datta

Example 3.2 : Find the mass and stiffness matrices
for the two models of 3D frame shown in Fig 3.5.
Solution :
Contd..

3
u

2
u

1
u
L

x

y
C.M.
L
k
k

g
x

Model-1
( (

( (
`
( (

( (
)
4 -2 2 4 -1 3 0
m
K = k -2 3 -2 ; M = -1 4 -3 ; I = 0
6
2 -2 3 3 -3 6 1
Fig3.5a
1/7
| |
T
eff g
m
P (model1) = - 3 -3 6 x
6
T.K. Datta
Contd..

g
x

u

C.M.
u
C.R.

v
L

k

k
Model-2
For Model -2
(
(
(
(

(
`
(
(

(
(
)
(

2
3 0 0.5L 1 0 0 0
K = k 0 3 0.5L ; M = m 0 1 0 ; I = 1
0.5L 0.5L 1.5L L 0
0 0
6
Fig3.5b
1/8
| |
T
eff g
P (model2) = -m 0 1 0 x
T.K. Datta
Example 3.3 : All members are inextensible for the
pitched roof portal; column & beam rigidities are K &
0.5K obtain mass matrix & force vector.

Solution:
For Model 1

Contd..
(
`
(
)
2.5 1.67 1
M = m I =
1.67 2.5 0

2
u

l
m

u
1

m
L
L

g x

2
m
3
L

g x

1
u

2
u
m
2
m

m
Model-1
Model-2
Fig3.6a Fig3.6b
1/9
T.K. Datta
(
` `
(
) )
eff g
1.406 -0.156 1 1.25
M = m I = P = -m x
-0.156 1.406 1 1.25
Contd..
For Model 2

C

B

m
m

D

A
E
2
m
Instantaneous Centre

o
C

l
B
u
D

A
E

m
2
m
sec
u
m
Unit acceleration given
to u
1
(model-1)

Unit acceleration given
to u
1
(model-2)

Fig3.6c Fig3.6d
1/10
T.K. Datta

For multi support excitation, equation of motion

Contd..
) 11 . 3 (
0
)
`
g g
t
gg gs
sg ss
g
t
gg gs
sg ss
g
t
gg gs
sg ss
P X
X
K K
K K
X
X
C C
C C
X
X
M M
M M

(3.12)
0 (3.13)
(3.14)
(3.15)
( ) ( )
( )
t
g
t t
ss sg g ss sg g ss g
t t t
ss ss ss sg g sg g sg g
t t t
ss ss ss sg g
ss ss ss sg ss g sg ss g
sg ss g
X X rX
M X M X C X C X K X
or M X C X K X M X C X K X
M X C X K X K X
M X C X K X M M r X C C r X
K K r X
= +
+ + + + =
+ + =
+ + =
+ + = + +
+
1
(3.16)
0 (3.17)
(3.18 )
0 (3.18 )
(3.19)
ss s sg g
s ss sg g g
ss sg
ss ss ss ss g
K X K X
X K K X rX a
K r K b
M X C X K X M rX
+ =
= =
+ =
+ + =
2/1
T.K. Datta
Contd..

Example 3.4 : Find the r matrices for the two frames
shown in Fig 3.7 & 3.8.
Solution :
For the rectangular frame

k
k

k

1 u
1

u
5

2 k

2 k
2 k

x
g1

2 m
Fig3.7
2/2
(
(

ss
3 -3
K = k
-3 9
(
(

sg
0 0 0
K =
-2k -2k -2k
(
(
(
(

gg
2k 0 0
K = 0 2k 0
0 0 2k
(
(
( (
(
( (
(
(

-1
ss sg
1 1
0 0 0 1 1 1
1 1
2 6
r = -K K = - =
1 1 -2k -2k -2k 1 1 1 k 3
6 6
..
..
x
g2
..
x
g3
u
3
u
4
m
u
2
T.K. Datta
Contd..
For the inclined leg portal frame
Unit rotation given
at B

1

B
(1)
(2)
(3)
3 L

D
(5)
C

(4)

B

A
E
L

(6)

(7)
Kinematic D.O.F.
Fig3.8
2/3
2
38.4 12 0 6 20 6 0
12 48 12 0 0 0 0
3.6
0 12 38.4 6 12 6 6
rr ru
EI EI
K K
L L

( (
( (
= =
( (
( (

3 3
24 16 12 12 8 5.53 8 4
16 181 0 16 5.53 52 5.33 6.33
12 0 12 0 8 5.33 8 4
12 16 0 12 4 6.33 4 3.69
uu
EI EI
K
L L

( (
( (

( (
=
( (
( (

3 3
1
19.56 10.51 4 8
10.51 129 5.33 22.3
0.0661 0.0054 4 8
0.0054 0.0082 5.33 22.31
0.2926 0.4074
0.654 0.1389
us usg
us usg
EI EI
K K
L L
r K K

( (
= =
( (

( (
= =
( (

(
=
(

T.K. Datta
Contd..
Example 3.5 : Obtain the r matrix for d.o.fs 1, 2 & 3 for
the bridge shown in Fig 3.9.

Solution: To solve the problem, following values are
assumed

2/4
Simplified model of a cable stayed bridge
Fig 3.9

60 m

(3)
Cables
1
l
20 m

(1)

(9)
240m
20 m

(2)

(10)

3

(6) 120m

(7)

4
50m
30m

(5)

2

(8)
120m

(4)

1

g
x

g
x

g
x

g
x
t d
EI =1.25EI =1.25EI;
1
0.8
480
deck
cable
AE AE
L
| |
| |
=
| |
\ .
\ .
12
Cos=
13
5
13
Sinu =
( ) ( ) ( )
; ;
3 3 3
1
AE 12EI 3EI 120m 12EI
= = =400m
l 80
120 80 120
T.K. Datta
( )
( )
( )
2 2
11 3
i
21 31
i
2
41 51 3
i
61 81 91 101
2
22 11; 32 31 71 52
1
62 51 72 41 82 92 102
33 3
1
3.75EI 2AE
k = + cos =1.875m+800mcos
l
80
AE
k =0; k =- cossin;
l
3 AE 3.75EI
k =- cos ;k =-
2 l
80
k =k =k =k =0
AE
k =k k =-k ; k =- cos ; k =0
2L
k =k ;k =k ;k =k =k =0
24EI 2AE
k = +
L
120
( )
2 2
43 53 63 73
sin =800m 1+sin ;
k =k =k =k =0
2/5
Contd..
T.K. Datta
( )
( )
;
| |
|
\ .
83 93 103
2
44 42 71 74
deck
54 64 84 94 104
55 65 75 85 95 105
3
66 76 86 96 106
3
77 87 97 107
88
6EI
k = - = -24000m;k =0;k = 24000m
L
AE
k = =320m;k =k k = -320m
480
k =k =k =k =k =0
3.75EI
k = ;k =k =k =k =k =0
80
3.75EI
k = ;k =k =k =k =0
80
k =320m;k =k =k =0
7EI
k =
12
( )
2
98 88 108
99 88 109 88 1010 88
7 2
= 400m 120 ;k = k ;k =0
0 12 7
7EI 8 2
k = = k ;k = k ;k =k
120 7 7
2/6
Contd..
T.K. Datta
(
(
(
(

-0.781 - 0.003 0.002 - 0.218
r = - -0.218 0.002 - 0.003 - 0.781
-0.147 - 0.0009 0.0009 0.147
2/7
Using the above stifness coefficients,the condensed
stifness matrix corresponding to the translational degees
of freedom is obtained.

The first 3X3 sub matrix is the stifness matrix corresponding
to the non support translational degrees of freedom.

The coupling matrix between the support and non support
translational degree of freedom is the upper 3X4 matrix.

Using them the above matrices the r matrix is obtained as

Contd..
T.K. Datta
Contd..
Equation of Motion in state space
Z = AZ + f (3.20)
in which
(
` `
(
) )
-1 -1
g ss ss ss ss
0 0 I x
Z = ; f = ; A = (3.21)
-rx -K M -C M x
t t
Z = AZ + f (3.22)
in which

` `
) )
t
t
-1
t
ss ss g
0
x
Z = ; f = (3.23)
-M K x
x
2/8
Example 3.6: Write equations of motion in state
space for example problem 3.4 using both relative &
absolute motions.
T.K. Datta

For relative motion of the structure

Contd..
2/9
2 2
1 2
k k k m
=1.9 ; =19.1 ; =0.105 ; =0.017
m m m k
( ( (
( ( (

ss
1 0 3 -3 0.156 -0.051
C = m+ k = km
0 2 -3 9 -0.051 0.205
(
(
(
(
(

2 2
2 2
0 0 1 0
0 0 0 1
A =
-3 1.5 -0.156 0.026
3 -4.5 0.051 -0.182
T.K. Datta
2/10
For absolute motion of the structure
( )
1 2 3
2
0
0
0
g g g
x x x

=
`

+ +
)
f
( )
( )

`

)
1 2 3
1 2 3
g g g
g g g
0
0
k
= ; f =
-0.33 x +x +x
m
-0.33 x +x +x
Contd..
T.K. Datta
Both time & frequency domain solutions for
SDOF system are presented first and then, they are
extended to MDOF system.

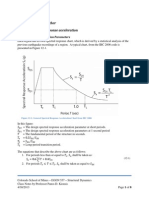
Two methods are described here: duhamel integration
&Newmarks - - methods.

Duhamel integration treats the earthquake force as a
series of impulses of short duration shown in the
figure.

In Newmarks method, the equation of motion is solved
using a step by step numerical integration technique.

For both methods, a recursive relationship is derived
to find responses at K+1 time station given those at K
time station.

|
t A
Response analysis
2/11
T.K. Datta
Contd..

g x

t

d t
t
t
( ) ( )
n
- t
1 d 2 d
x t =e Ccos t +C sin t (3.24)
( ) ( ) ( )
(

n
- t
n 1 2 d d d 1 n 2 d
x t =e - C +C cos t + - C - C sin t (3.25)
Fig3.10
Duhamel Integration:
t = t - t (3.34)
k+1 k
( )
| |
|
\ .
k+1 k
k
F - F
F =F + (3.35)
t
2/12
T.K. Datta

Responses at the t
k+1
is the sum of following :

Response for initial condition

Response due to F
k
between t
k
and t
k+1

Response due to triangular variation of F

Response at t
k+1
clearly depends upon

The constants etc can be evaluated from the
three response analyses mentioned above.

Contd..
(0) 0 (0) 0 x x = =
x = C x +C x +C F +C F (3.36)
1 4 k+1 k 2 k 3 k k+1
x = D x +D x +D F +D F (3.37)
1 4 k+1 k 2 k 3 k k+1
2
x = -x - 2 x - x (3.38)
n n
k+1 gk+1 k+1 k+1
C ,C
1 2
2/13
T.K. Datta
Contd..
k+1 k k+1
(3.49) q = Aq +HF
in which

` `

)

)
i 4
i i 4
2
i
n 4 n 4
x C
q = x H= D (3.50)
x 1
- 2 D - C
m
{ } { }
{ }
( )
( )
( )
( )
(
(
(
(
(
(

(
` ` `
( )
) )

1 3 2 3 3
1 3 2 3 3
2 2
3 n 1 3 n 2 3
n 3 n 1 3 n 2 3
C +kC C +cC m C
A = D +kD D +cD mD (3.51)
-m C - C +kC - C +cC
-2 mD -2 D +k D -2 D +cD
2/14
Using expression for these constants, the respons at
can be written in recursive form as
t
k+1
T.K. Datta
(
| |
( |
( |
|
(
\ .

(
| |
( |
( |
\ .

(
| |
| | | |
( |
| |
( |
| |
|
\ . \ .
(
\ .

- t

n
C =e cos t + sin t (3.39a)
1 d d
2
1-
- t
1
n
C =e sin t (3.39b)
2 d
d
2
- t
1 2 2 1- 2
n
C = +e - 1+ cos t + - sin t
3 d d k t t t
2
n n
1- d

`
)

(
| |
| | | |

( |
| |
`
| | ( |

\ . \ .
\ .

)
(3.40)
2
- t
1 2 2 2 -1
n
C = 1- +e cos t + sin t (3.41)
4 d d k t t t
n n
d
Contd..
2/15
T.K. Datta
( | |
( |
( |
|
(
\ .

( | |
( |
( |
|
(
\ .

( | |
| | | | ( |
`
| |
( |
\ . \ .
|
(
\ .
)
- t
n n
D =e - sin t (3.42)
1 d
2
1-
- t

n
D =e cos t - sin t (3.43)
2 d d
2
1-
- t
1 1 1
n n
D = - +e cos t + + sin t (
3 d d k t t
2 2
1- t 1-
( | |
( |
`
( |
|
(
\ .
)
3.44)
- t
1
n
D = 1- e cos t + sin t (3.45)
4 d d kt
2
1-
Contd..
2/16
T.K. Datta
Contd..
Newmarks - method:

With known displacement, velocity & acceleration at kth
time, it calculates the corresponding quantities at k+1th
time; F
k+1
is known.

Two relationships are used for this purpose; they mean
that within time interval , the displacement is
assumed to vary quadratically.

Substituting these relationships in the equation of
motion & performing algebraic manipulation,
following recursive relationship is obtained.
|
t A
( )
( ) ( )
| |
|
\ .
k+1 k k k+1
2 2
k+1 k k k k+1
x = x + 1- x t +x t (3.52)
1
x = x +x t + - t x + t x (3.53)
2
3/1
T.K. Datta
Contd..
k+1 N k N k+1
(3.66) q =F q +H F
( )

` ` `
)

)
)
2
i
i i N
i
x t
1
q = x H = t (3.67)
m
x 1
( ) ( ) ( ) ( ) ( )( )
( ) ( )
(
(
(
(
(
(
(

2 2 3 2 2
2 2
n n n
2
2 2
N n n n
2 2
n n n
1
- t t - 2 t - t t - + t
2
1
F = - t - 2 t - t t - + t
- -2 - t -
(3.68)
in which
3/2
( )
2
2
1 2
n n
t t o e o e | = + A + A
T.K. Datta

With known responses at kth time step, responses
at k+1 th time step are obtained.

State space solution in time domain
( )
( )
( ) ( )
( )
(

(
` `
(
)
)

}
}
0
0
k+1
k+1
k
g
g
g
t
A t-t
At -As
0 g
t
t
At At -As
k+1 k g
t
Z= AZ+f (3.69)
0 1
0
x
A = f = Z= (3.70)
k c
-x
x - -
m m
Z t = e Z t +e e f s ds (3.71)
Z = e Z +e e f s ds (3.72)
3/3
T.K. Datta
Eqn (3.73) is preferred since it does not require
inversion.

Once Z is known, displacement and velocity are
known.

Second order differential equation is solved to find the
acceleration .
Contd..
( )
At At
Z = e Z + t e f (3.73)
k+1 k gk
At -1 At
Z = e Z + A e - I f (3.74)
k+1 k gk
At t -1
e = e (3.75)
The integration in Eqn (3.72) can be performed in two
ways.
3/4
T.K. Datta
It obtains steady state solution of the equation of
motion & hence, not strictly valid for short
duration excitations like, earthquake.

However, under many cases (as mentioned before) a
good estimate of rms & peak values of response may
be obtained.

For obtaining the response, ground motion is Fourier
synthesized and responses are obtained by the use of
the pair of Fourier integral (discussed before) .

Frequency domain analysis
( ) ( )
( ) ( )
}
}
-it
g g
-
it
g g
-
1
x i = x t e dt (3.76)
2
x t = x i e d (3.77)
3/5
T.K. Datta

The FFT algorithm now available solves the integral
using their discrete forms.

For linear systems, the well known response
equation in complex frequency domain is used:

For earthquake excitation, the response due to the
jth frequency component of excitation is given by
Contd..
( )
( )
N-1
-i 2kr N
gk gr
r=0
N-1
i 2kr N
gr gk
k=0
1
x = x e (3.78)
N
x = x e (3.79)
x(i )= h(i)p(i)
( ) ( ) ( )
j
it
j j gj
x t =h i x i e (3.80)
3/6
T.K. Datta

Total response is given by
N/2
j
j=0
x(t)= x(t)
Contd..
in which
( ) ( )
(

-1
2 2
n j n j
j
h i = - +2i

The following steps may be used for programming
the solution procedure.
Sample at an interval of (N).

Input in FFT.

Consider first N/2+1 values of the output

Obtain
( )
g
x t t A
( 0... 1)
gr
x r N =
( )
e
N
T t
t
e =
+ A
| |
|
\ .
j j
N
h(i ); =0...
2
3/7
T.K. Datta
Contd..
Obtain .

Add to make input for IFFT.

IFFT of gives .
j j gj
x(i )= h(i)x (i)
*
j
x(i )
*
j
x(i )j =0...N-1
( ) x t

Since both frequency & time domain ( Duhamel
integration) can be used for the solution, there exists
a relation between and .

This relationships forms Fourier transforms pair of
integral.

) (e h
) (t h
( ) ( )
( ) ( )
}
}
-it
-
it
-
h i = h t e dt (3.83)
1
h t = h i e dt (3.84)
2
3/8
T.K. Datta
Contd..
Example 3.7:Single bay portal frame in Fig 3.11 is
subjected to Elcentro earthquake. Find with

Solution:
For Duhamel integral

n
d
t =0.02s
=12.24 rad/s
=12.23rad/s
0.0150 0.0312 0.0257 0.0098
0.5980 0.9696 0.0146 0.0060
1.5153 3.4804 0.0436 1.0960

( (
( (
= =
( (
( (

A H
( (
( (
( (
( (

n n
0.9854 0.0196 0.0001 0.0001
F = -1.4601 0.9589 0.0097 H = 0.0097
-146.0108 -4.1124 -0.0265 0.9735
3/9

m
m
, EI L

u
, EI L

60
o

k
L
3
= 12EI

10 rad/sec k
m
=

g x

60
o

, EI L
For New Marks method
( ) x t
(0) 0; (0) 0; 0.05 x x = = =
Fig 3.11
T.K. Datta
Contd..
For state space solution
( (
( (

(
(

At
0 1 -0.0161- 0.16045i -0.0161+0.16045i
A = =
-37.50 -1.2247 0.9869 0.9869
0.9926 0.0197
e =
-0.7390 0.9684
Responses for first few time steps are given in Table
3.1 and 3.2.(in the book)

Time history of responses are shown in Fig.3.12
3/10
T.K. Datta
0 4 8 12 16 20 24 28 30
-0.1
-0.05
0
0.05
0.1
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

0 4 8 12 16 20 24 28 30
-0.1
-0.05
0
0.05
0.1
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

Newmarks-|-method
Frequency domain FFT analysis
Fig3.12
Contd..
3/11
T.K. Datta
Response of MDOF system
Two types of analysis are possible: direct & modal
analysis.

For direct analysis damping matrix is generated using
Rayleigh damping,

For modal analysis, mode shapes & frequencies are
used & modal damping is assumed the same for all
modes.

Both time & frequency domain analyses using second
order & state space equations can be carried out.

Frequency domain analysis uses FFT algorithm.
C= M + K
4/1
T.K. Datta
Direct analysis in time domain
Equation of motion takes the form.

The same two equations as used in SDOF are used by
replacing x by vector X

Substituting those two equations in equation (3.85),
the solution is put finally in the recursive form

MX +CX +KX = -MrX (3.85)
k+1 k+1 k+1 gk+1
( )
( ) ( )
| |
|
\ .
k+1 k k k+1
2 2
k+1 k k k k+1
x = x + 1- x t +x t (3.86)
1
x = x +x t + - t x + t x (3.87)
2
( )
k+1 N k N gk+1
Q =F Q +H X 3.92
4/2
Contd..
T.K. Datta
Contd..
{ }
{ }
{ }
(

` (
)
(
(

(
`
(
)
(

(
`
(
)

2 2 2 2 2
2
N
2
St t t Qt St t
I - I t - Q+St I - +
4 4 4 2 4 4
St t t Qt St t
F = - I- Q+St I - + (3.93)
2 2 2 2 4 2
Qt St
-S - Q+St - +
2 4

`

)
2
-1 -1 -1
N
t
-T
4
t
S=G K Q=G C T =G Mr H = -T (3.94)
2
-T
4/3
2
G M C t K t o | = + A + A
T.K. Datta
Frequency domain analysis using FFT

Using the steps mentioned before for SDOF X(t)
is obtained using FFT & IFFT

Note that the method requires inversion of a
complex matrix Eq.(3.98)

Contd..
{ }
( ) ( ) { }
( ) ( ) ( )
( )
....
......
(

T
g 1 2 n g
T
g g 1 11 g1 12 g2 13 g3 2 21 g1 22 g2 23 g3
j j gj
-1
2
j j j
P =- m m m x (3.95 )
P =-Mr X =- m r x +r x +r x ,m r x +r x +r x , (3.96 )
X i =H i P i (3.97 )
H i = K-M +i C (3.98 )
4/4
T.K. Datta
Contd..
Example 3.8 : For the portal frame shown in Fig 3.7 ,
find the displacements by Newmarks method:
time delay = 5 s; k/m = 100; = 5%; duration = 40s

: Last 10s of record have zero values

: First 5s & last 5s have zero values

: First 10s have zero values
1
g
x
2 g
x
3
g
x

m

k
k

k

1
u
1

2 u
2

2 k

2 k
2 k

2 m
Fig3.7
4/5
Solution:
x
g2
x
g3
x
g1
.. .. ..
u
3
u
4
u
5
T.K. Datta
Equation of motion can be written as:
1 2
12.25 / ; 24.5 / ; 0.816; 0.0027; 0.02 rad s rad s t s e e o | = = = = A =
Contd..
1
2
3
1 1 1
2 2 2
1 0 1 0 3 3 3 3
0 2 0 2 3 9 3 9
1 0 1 1 1
0 2 1 1 1 3
g
g
g
x x x
m m k k
x x x
x
m
x
x
o |

( ( ( (
+ + +
` ` ` `
( ( ( (

) ) )
)

( (
=
`
( (

)
0.9712 0.0272 0.0193 0.0006 0.0001 0.0
0.0132 0.9581 0.0003 0.0192 0.0 0.0001
2.8171 2.7143 0.9281 0.0611 0.0096 0.0003
1.3572 4.1751 0.0302 0.8973 0.0002 0.0094
281.7651 271.4872 7.1831 6.1402 0.0432 0.0343
135.7433 417.5
n

=
F
091 3.0701 10.2531 0.0171 0.0602
(
(
(
(
(
(
(
(

(

4/6
T.K. Datta
| |
0
0 0
T
x =
Contd..
0.0 0.0 0.0
0.0 0.0 0.0
0.0033 0.0033 0.0033
;
0.0032 0.0032 0.0032
0.3301 0.3301 0.3301
0.3182 0.3182 0.3182
n

(
(

(
(
=
(

(
(

(

(

H
Using recursive Eqn. (3.92), relative displacement,
velocity and accelerations are obtained.

Time histories of displacements, (u
1
and u
2
) are
shown in Fig 3.13
4/7
T.K. Datta
Contd..
0 5 10 15 20 25 30 35 40
-0.04
-0.02
0
0.02
0.04
Time (sec)

D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

0 5 10 15 20 25 30 35 40
-0.02
-0.01
0
0.01
0.02
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

Displacement u
1
Displacement u
2
Fig3.13
4/8
T.K. Datta
Example 3.9: For the pitched roof portal frame shown
in Fig 3.8, find displacements 4 & 5 for zero & 5s time
delay between the supports.

Contd..

1

A

E
1
Unit displacement given
at A
Unit displacement given
at E
Fig3.8
1/ 2
3
2 / ; 5%
EI
rad s
mL

| |
= =
|
\ .
1 2
5.58 / ; 18.91 / ; 0.4311; 0.004; 0.02 rad s rad s t e e o | = = = = A =
4/9
Solution:
T.K. Datta
For the first case , duration is 30s and excitation are
same at all supports.

For the second case, duration = 35 s and excitations
are different at different supports.
Contd..
3
2.50 1.67
;
1.67 2.50
16 10.50
10.50 129
0.2926 0.4074
0.654 0.139
m
EI
L
(
=
(

(
=
(

(
=
(

M
K
r
Time histories of displacements are shown for the
two cases in Fig3.14
4/10
T.K. Datta
4/11
0 4 8 12 16 20 24 28 32 36
-0.1
-0.05
0
0.05
0.1
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

0 4 8 12 16 20 24 28 32 36
-2
-1
0
1
2
x 10
-3
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

Without time delay for the d.o.f. 4
Without time delay for the d.o.f. 5
Contd..
T.K. Datta
Contd..
0 5 10 15 20 25 30 35 40
-0.05
0
0.05
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

0 5 10 15 20 25 30 35 40
-4
-2
0
2
4
x 10
-3
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

With time delay for the d.o.f. 4
With time delay for the d.o.f. 5
Fig3.14
4/12
T.K. Datta
The excitation vector f
g
is of size 2nX1 (single point)

The excitation vector f
g
is of size 2nX1 (multi point
excitation).

The time domain analysis is performed in the same
way as for SDOF system.

In frequency domain, state space solution can be
performed as given below

g g
p rx =
0
(3.99)
g g
x

=
`
)
f
r
0
(3.100)
g
g

=
`
)
f
p
5/1
Contd..
State Space Direct Analysis
T.K. Datta
Contd..
(3.101)
g
= + z Az f
in which
1 1
0
; ; (3.102)
g g g
g
x
and
x

(
= = = =
` `
(

)
)
0 I
A f z p rx
p
KM CM
By using FFT of , j
th
component of is
obtained.

jth frequency component of response is given by:
) ( e i f
gj
g
f
( ) ( ) ( )
( )
1
(3.103)
(3.104)
j j gj
j
i i i
i
e e e
e e

=
(
=

z H f
H I A
By using IFFT, may be obtained (as before)
( ) z t
5/2
T.K. Datta
Contd..
Example 3.9: Find the displacement, responses
corresponding to d.o.f 1,2 and 3 using frequency
domain ordinary & state space solutions for the beam
shown in Fig 3.15
3
3
16; 48 ; 0.6 ; 2%
s s
EI
k m C m
mL
= = = =
5/3
A pipeline supported on soft soil (Exmp. 3.10)
(1) (2) (3)

2 m

m
(4)
2 m

s
k

s
c

g
x

L
L
(5) (6)
(7)
Wave propagation

s
k

s
c

g
x

s
c

s
k

g
x

T.K. Datta
0.0 0.0 0.0 1.0 0.0 0.0 0
0.0 0.0 0.0 0.0 1.0 0.0 0
0.0 0.0 0.0 0.0 0.0 1.0 0
112.0 16.0 16.0 1.622 0.035 0.035 1
32.0 80.0 32.0 0.070 0.952 0.070 1
16.0 16.0 112.0 0.035 0.035 1.622 1
g
m
(
(
(
(

= =
( `

(
(

(

(
)
A f
g
x
Contd..
For solution of second order differential equation,
FFT & IFFT are used as before.
5/4
1 2 3
56 16 8 0.813 0.035 0.017
16 80 16 0.035 0.952 0.035
8 16 56 0.017 0.035 0.813
8.1 / , 9.8 / , 12.2 /
0.1761 0.0022
m m
rad s rad s rad s e e e
o |

( (
( (
= =
( (
( (

= = =
= =
K C
Solution:
T.K. Datta
0 5 10 15 20 25 30
-0.1
-0.05
0
0.05
0.1
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

0 5 10 15 20 25 30
-0.2
-0.1
0
0.1
0.2
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

Displacement for d. o. f. 1
Contd..
Fig3.16
5/5
Time histories of displacements are shown in
Fig 3.16 - 3.17
T.K. Datta
Fig3.17
15 20 25 30 35 40 45
-0.1
-0.05
0
0.05
0.1
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

15 20 25 30 35 40 45
-0.2
-0.1
0
0.1
0.2
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

Contd..
5/6
T.K. Datta
Excitation load vector P
g
is of the form

Generally is set to zero (in most cases)

The solution procedure remains the same.

and are of the order of n x s; s is the number
of supports.

Solution requires time histories of and .

Solutions can be obtained both in time and frequency
domains.
Solution for absolute displacements
( )
(3.105)
g sg g sg g
= + P K x C x
sg
C
sg
k
sg
C
g
x
g
x
5/7
T.K. Datta
Modal analysis
In the modal analysis, equation of motion is decoupled
into a set of N uncoupled equations of motion .

Normal mode theory stipulates that the response is a
weighted summation of its undamped mode shapes.
( )
....
T
i i i i i i i g
T 2
i
i i i i i i i i
i
s
2
i i i i i ik gk
k=1
T
i k
ik
T
i i
X = z (3.106)
mz +c z +k z = - Mrx (3.111)
k
k = K = c = 2 m (3.112)
m
z +2z + z = - x i =1 m (3.113)
Mr
= (3.114)
M
5/8
T.K. Datta
For s=1, equation 3.113 represents the equation for
single point excitation.

Each SDOF system can be solved in time or
frequency domain as describes before.

Example 3.11: For the cable stayed bridge shown
before , find the displacement responses of d.o.f 1,2,3
for Elcentro earthquake; 5s time delay is assumed
between supports.
Contd..
684 0 149 20 0 0
0 684 149 0 20 0
149 149 575 0 0 60
m m
( (
( (
= =
( (
( (

K M
5/9
Solution:
T.K. Datta
Contd..
| |
| |
| |
(
(
(
(

1 2 3
T
1
T
2
T
3
-0.781 - 0.003 0.002 - 0.218
r =- -0.218 0.002 - 0.003 - 0.781
-0.147 - 0.0009 0.0009 0.147
=2.86rad/s =5.85rad/s =5.97rad/s
= -0.036 0.036 -0.125
= 0.158 0.158 0
= -0.154 0.154 0.030
First modal equation

`

)
g1
T
g2
2
1
1 1 1 1 1
T
g3
1 1
g4
x
x
Mr
z +2 z + z =-
x
M
x
5/10
T.K. Datta
| |
1
2
1
3
4
1.474 0.008 0.0061 1.474
g
g
g
g
g
x
x
p
x
x

=
`

)
0.025 t A =
will have first 30s as the actual record & the last
15s as zeros.

will have first 10s as zeroes followed by 30s of
actual record & the last 5s as zeros.

Time histories of generalized loads are shown in
Fig3.18.

Time histories of generalized displacement are
show in Fig 3.19
1
g
x
3
g
x
Contd..
5/11
T.K. Datta
0 5 10 15 20 25 30 35
-1
-0.5
0
0.5
1
Time (sec)
S
e
c
o
n
d

g
e
n
e
r
a
l
i
z
e
d

f
o
r
c
e
(
g
)

0 5 10 15 20 25 30 35
-1
-0.5
0
0.5
1
Time (sec)
F
i
r
s
t

g
e
n
e
r
a
l
i
z
e
d

f
o
r
c
e
(
g
)

First generalized force
Second generalized force (p
g2
)
Fig3.18
Contd..
5/12
T.K. Datta
Contd..
0 5 10 15 20 25 30 35 40 45
-0.04
-0.02
0
0.02
0.04
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

0 5 10 15 20 25 30 35 40 45
-0.04
-0.02
0
0.02
0.04
Time (sec)
D
i
s
p
l
a
c
e
m
e
n
t

(
m
)

First generalized displacement (Z
1
)
Second generalized displacement (Z
2
)
Fig3.19
5/13
T.K. Datta
Contd..
Solution
Z
1
Z
2
Z
3
Time history
rms
(m)
peak
(m)
rms
(m)
peak
(m)
rms
(m)
peak
(m)
0.0091 0.0369 0.0048 0.0261 0.0044 0.0249
Frequency
domain
0.009 0.0368 0.0049 0.0265 0.0044 0.0250
1
z
2
z
3
z
5/14
Table 3.4 Comparison of generalized displacement
T.K. Datta
One index which is used to determine number of
modes required is called mass participation factor.

Number of modes m to be considered in the
analysis is determined by
i r ir
r
i
m
M
|
=

Contd..
1
1
m
i
i

=
~
5/15
Number of modes depends upon the nature of
excitation, dynamic characteristics of structure &
response quantity of interest.
T.K. Datta
The approach provides a good estimate of response
quantity with few number of modes.
) (t R
Mode acceleration approach
| |
( )
( ) ( )
(

i i g i i i
2 2
i i
m m
i
i g i i i i
2 2
i=1 i=1
i i
m
i i i i
2
i=1
i
1 1
z = - x - z +2z (3.117)

1
R(t) =- x - z +2z (3.118)

1
=R t - z +2z (3.119)
is the quasi static response for which

can be proved as below
g
Mrx
( ) ( )
( ) ( )
g
T T
g
KX t =-Mrx t (3.120)
Kz t =- Mr x t (3.121)
6/1
T.K. Datta
The solution is obtained by:

Find quasi static response for .

Find :

The second quantity is obtained from
( )
1
1
2
m
i i i i
i i
z z e |
e
=
+
) (t R
Contd..
( )
;

n n
i g i g
i i i i
2 2
i=1 i=1
i i
- x x
z = R t = z =- (3.122,123)

g
Mrx
( )
| |
|
\ .
i g
i i i i
2 2
i i
- x
1
z +2z = - z (3.124)

6/2
The contribution of the second part of the solution
from higher modes is small; first part contributing
maximum to the response consists of contribution
from all the modes.
T.K. Datta
Computation of internal forces
Determination of internal forces may be
obtained in two ways:

Using the known displacements and member
properties.

Using the mode shape coefficients of the internal
forces.

For the latter , any response quantity of interest is
obtained as a weighted summation of mode shapes;
the mode shape coefficients correspond to those
of the response quantities of interest.

The method is applicable where modal analysis is
possible;number of modes to be considered depends
upon the response quantity of interest.

6/3
T.K. Datta
Contd..
6/4
These coefficients are obtained by solving the MDOF
system for a static load given below & finding
the response quantity of interest.

For the first approach member stiffness matrix is
multiplied by displacement vector in member
co-ordinate system.

Rotations which are condensed out are regenerated
from the condensation relationships.

The second approach is widely used in software
which deals with the solutions of framed structure
in general.
2
; 1 (3.125)
i i i
i m e = = | P M
T.K. Datta
z(t) is expressed as a weighted summation of mode
shapes.

Equation of motion can be then written as

2n uncoupled equations are then obtained as

The initial condition is obtained from

State space analysis
( )
Z t =q (3.126)
g
-1 -1 -1
g
q= Aq+f (3.127)
q= Aq+ f (3.128)
( )
i i i gi
q = q + f i =1.......2n (3.129)
-1
0 0
q = Z (3.130)
6/5
T.K. Datta
In frequency domain, Eq 3.129 is solved using the
same FFT approach with
Contd..
( ) ( )
1
1
(3.131)
j
h i e e

=
Example 3.12: For the frame shown in Fig3.20, find
the base shear for the right column; k/m = 100; 5% =

k
k

k
k

2 k

2 k

2 k

2 k

g x

4 u

3 u

2 u

1 u

m

2 m

2 m

2 m
Fig3.20
Solution:
2 2 0 0
2 4 2 0
0 2 6 4
0 0 4 8
k
(
(

(
=
(
(

K
1 0 0 0
0 2 0 0
0 0 2 0
0 0 0 2
m
(
(
(
=
(
(

M
1 2
5.06rad/s; 12.57rad/s e e = =
3 4
18.65rad/s; 23.85rad/s e e = =
6/6
T.K. Datta
| |
| |
| |
| |
1.0 0.871 0.520 0.278
1.0 0.210 0.911 0.752
1.0 0.738 0.090 0.347
1.0 0.843 0.268 0.145
T
T
T
T
=
=
=
=
1
2
3
4
|
|
|
|
Contd..
1.500 1.140 0.0 0.0
1.140 3.001 1.140 0.0
0.0 1.140 4.141 2.280
0.0 0.0 2.280 5.281
m o |
(
(

(
= + =
(
(

C M K
0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0
2.0 1.0 0.0 0.0 1.454 0.567 0.0 0.0
2.0 2.0 1.0 0.0 1.134 1.495 0.567 0.0
0.0 1.0 3.0 2.0 0.0 0.567 2.062 1.134
0.0 0.0 2.
=

A
0 4.0 0.0 0.0 1.134 2.630
(
(
(
(
(
(
(
(
(
(
(
(

6/7
T.K. Datta
Time histories of the base shear obtained by mode
simulation, mode acceleration and modal state space
analyses are shown in Fig 3.21.
Contd..
1 2
3 4
1.793 1.571 ; 1.793 1.571 ;
1.157 1.461 ; 1.157 1.461
i i
i i

= + =
= + =
0 5 10 15 20 25 30
-0.1
-0.05
0
0.05
0.1
Time (sec)
S
h
e
a
r

(
i
n

t
e
r
m
s

o
f

m
a
s
s

m
)

0 5 10 15 20 25 30
-0.1
-0.05
0
0.05
0.1
Time (sec)
S
h
e
a
r

(
i
n

t
e
r
m
s

o
f

m
a
s
s

m
)

Mode acceleration method
State space method
10
2
10
2
6/8
Fig 3.21
T.K. Datta
Computational steps for MATLAB programming
are given in the book in section 3.5.7 for all
types of analyses.

Steps are given in following sections:
Contd..
Computation of basic elements required for all
types of analysis.

Time domain analysis covering direct analysis,
modal analysis, mode acceleration approach,
state space analysis (modal and direct).

Frequency domain analysis covering all
cases considered for the time domain analysis
6/9
T.K. Datta
Lec-1/74
T.K. Datta

Chapter -4
FREQUENCY DOMAIN
SPECTRAL ANALYSIS
T.K. Datta
Introduction
Spectral analysis is a popular method for finding
seismic response of structures for ground motions
modeled as random process.

Since the analysis is performed in frequency domain
it is known as frequency domain spectral analysis.

The analysis requires the knowledge of random
vibration analysis which forms a special subject.

However, without the rigors of the theory of random
vibration, spectral analysis is developed here.

It requires some simple concepts which will be
explained first.

1/1
T.K. Datta
Stationary random process

x
2
(t)
x
1
(t)
t
1
t
2

x
3
(t)
x
4
(t)

1
( ) x t
1
( ) x t
Fig 4.1
Mean of is
2 2
1 1
[{ ( ) ( )} ]
X
E x t x t o =
Sample
2 2
1
[ ( ) ( )]
i
xi i i T
x t x t dt o =
}
Ergodic process
2 2
x xi
o o =
1/2
T.K. Datta
Fourier series & integral
Fourier series decomposes any arbitrary function
x(t) into Fourier components.

( )
| |
|
\ .
} }
}
0
k k
k=1
T T
2 2
k 0
T T
- -
2 2
T
2
k
T
-
2
a 2kt 2kt
x(t ) = + a cos +b sin (4.1)
2 T T
2 2kt 2
a = x(t )cos dt a = x t dt (4.2)
T T T
2 2kt
b = x(t )sin dt (4.3)
T T
1/3

} `

)
T
2
o
k k
T
2
a
x(t ) = + x(t )cos( t )dt cos( t )+
2
k=1
-
(4.4)
e
e e
t

A
} `

)
T
2
k k
T
2
x(t )sin( t )dt sin( t )
k=1
-
T.K. Datta
( ) ( )
} }
} }

=0 =0

- -
x(t ) =2 A( )cos(t )d+2 B()sin(t )d (4.7a)
x(t ) = A cost d+ B sin t d (4.7b)
Contd.
The complex harmonic function is introduced
to define the pair of Fourier integral.

}
it
-
(4.10) x(t ) = x( )e d
, 2 / T T d e t e A =
. It can be shown that (book)
1/4
}
-it
-
1
x( )= A()- i B()= x(t )e dt (4.9)
2
T.K. Datta
Contd.
Discrete form of Fourier integral is given by

| |
|
\ .
| |
|
\ .
2kr
N-1
-i
N
k r
r=0
2kr
N-1
i
N
r k
k=0
1
x( )= x e (4.12)
N
x(t ) = x e (4.13)
FFT & IFFT are based on DFT.

From , Fourier amplitude is obtained.

x
k
A
k
( )
2 2
k k k
0 0
N
A = 2 c +d k =1...... (4.14)
2
A = c (4.15)
For the Fourier integral to be strictly valid
}
-
x(t ) dt < (4.11)
1/5
T.K. Datta
In MATLAB, , is divided by N/2 (not N), then

Parsavels theorem is useful for finding mean
square value

Note equation 4.18 pertains to Eq 4.1 & Eq 4.19
pertains to Eqs 4.12 4.13.
(X(t) is divided by N not N/2 as in MATLAB)

r
x
Contd.
( )
2 2
k k k
0
0
A = c +d (4.16)
c
A = (4.17)
2
}

}
T 2
2 2 2
0
k k
0
T
N-1 N-1
2
2 2
r k
r=0 K=0
0
a 1 1
x(t )dt = + (a +b ) (4.18)
T 4 2
1 1
x(t )dt = x = x (4.19)
T N
1/6
T.K. Datta
Correlation functions
Random values taken across the ensemble
are different than those would take
although and are the same.

How these two sets of random variables are
different is denoted by auto correlation function

Obviously, mean square value of the
process & the two sets are perfectly correlated.

Similarly, cross correlation between two random
process is given by

1
x(t )
2 1
x(t = t + )
2
1
E [x(t )]
2
2
E [x(t )]
XX
R ( =0) =
| |
yx xy
xy 1 1
( ) R ( )=E x(t )y(t + ); R =R (- ) (4.21)
1/7
xx 1 1
R ( )=E[x(t )x(t + )] (4.20)
T.K. Datta

E [x
2
] = o
2
+ m
2

x R (t)

2 m

t

o
o
2
+ m
2

0
t

o

xy R
(t)
o
x
o
y
+m
x
m
y
m
x
m
y
o
x
o
y
+m
x
m
y
Fig 4.2
Fig 4.3
Contd.
1/8
T.K. Datta
PSDFs & correlation functions
Correlation functions & power spectral density
functions form Fourier transform pairs

From equation 4.23, It follows

e
e
}
}
}
}
-iw
xx xx
-
-iw
xy xy
-
iw
xx xx
-
iw
xy xy
-
1
S ( )= R ()e d (4.22)
2
1
S ( )= R ()e d (4.23)
2
R ( )= S ()e d (4.24)
R ( )= S ()e d (4.25)
yx xy
S ( )= comp.conjugS ()
1/9
T.K. Datta
An indirect proof of the relationships may be
given as
Contd.
| |
(
}
}
2 2
xx x xx
-
xy xy
-
R (0) =r = S ( )d=E x (4.26a)
R (0) = S ( )d=E xy (4.26b)
Eq. 4.26a provides a physical meaning of PSDF;
distribution of mean square value of the process
with frequency.

PSDF forms an ideal input for frequency domain
analysis of structures for two reasons:
1/10
T.K. Datta
A second order random process is uniquely
defined by its mean square value.

Distribution of mean square value with frequency
helps in ascertaining the contribution of each
frequency content to the overall response.

Contd.

S (e)

d e
e

e
Fig 4.4
1/11
T.K. Datta
1/12
Contd
Fig 4.5(b) Fig 4.5(a)

k
S

2 T t

k
e
e
S = | x | at kth frequency

k
e
e

k
S
Compactedordinates
S at closer frequencies

S (e)

e e
k
kth ordinate of the power spectral density function
Fig 4.5(c)
T.K. Datta
Concept of PSDF becomes simple if ergodicity is
assumed;for a single sample, mean square value

For large T , ordinates become more packed; kth
ordinate is divided by ; sum of areas will
result in variance; smooth curve passing through
points is the PSDF.

This definition is useful in the development of
spectral analysis technique for single point
excitation and widely used in the random
vibration analysis of structures.

e d
Contd.
( )

}
T
2
N-1
2
2 2 2 2
0
x k k k
k=0
0
a 1 1
r = x(t ) dt = + a +b = x (4.27a)
T 4 2
1/13
T.K. Datta
It is difficult to attach a physical significance to
cross PSDF; however some physical significance
can be understood from the problem below.

For different values of , degree of correlation
varies; the responses will be different.

Contd.

1
P
1
=

A sin et
P
2
=

A sin (et + |)

For random excitations & ,the response
will be obviously different depending upon the
degree of correlation & hence cross PSDF.
1
p(t )
2
p(t )
1/14
T.K. Datta
PSDF matrix is involved when more than one
random processes are involved

PSDF matrix
( ) ( ) ( )
( ) ( )
( ) ( ) ( )
1 1 2 2
1 2 2 1
1 1 2 2 1 2
1
1 1 2 2 1 2
2
2 2 2 2 2
1 1 2 2 1 2 1 2 2 1 2 1
2 2
1 2
1 2 2 1
2 2
1 2 1 2
[ ] (4.28)
(4.30)
yy x x x x
x x x x
yy x x x x x x
x
y a x a x a a
x
E y E a x a x a a x x a a x x
S d a S d a S d
a a S d a a S d
S d a S a S a a S
o o o
o o o
o o
o o
o
o
e e e e e e
e e e e
e e e e

= + =
`
)
( ( = + + +

= +
+ +
= + +
} } }
} }
}
( ) ( )
{ }
2 1
1 1 2 2 1 2 2 1
2 1
1 1 1 2 1 2 2
1 2 1 2 2 1 1 2
2 1 2 2 2
yy
(4.31)
(4.32 )
S (4.32 )
x x
x x x x
yy x x x x x x x x
x x x x
a a S d
S S a
S a S a S a a S a a S a a a
S S a
b
o
o
e e e
( +

(
= + + + =
`
(
)
=
}
T
xx
aS a
2/1
T.K. Datta
For single variable

Eq (4.32b) can be extended to establish two
stochastic vectors
Contd.
2
y x
S =a S (4.33)
( ) ( )
( ) ( ) ( )
1 1 2 2 1 2 2 1
nm
n1 m1
T
yy xx
nm 1 nr 2
m1 r1
T T T T
yy x x x x x x x x
xy xx
y t = A x t (4.34)
S = AS A (4.35)
y t = A x t +B x t (4.36)
S = AS A +BS B +AS B +BS A (4.37)
S = AS (4.38)
PSDF of the derivatives of the process is
required in many cases. It can be shown (book):
2
x x
2 4
x x x
S = S (4.48)
S = S = S (4.49)
2/2
T.K. Datta
It is assumed that p(t) is an ergodic process; then in
frequency domain

From (4.51a), it is possible to write

Using Eq(4.19), mean square value may be written as

SISO
x()=h()p() (4.51a)
2 2 -1
n n
g
h( )=( - +2i ) (4.51c)
p( )=-x() (4.51d)
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
* * *
2 2 2
x x =h h p p (4.53a)
x = h p (4.53b)

}
}
T
N-1 N-1
2 2
2 2
r K
r=0 K=0
0
T
2 2
2
0
1 1
x(t )dt = x = x = x( ) (4.54)
T N
1
x(t ) dt = h( )p() (4.55)
T
2/3
T.K. Datta
For & use of equations 4.27a-c, Eqn 4.55
gives

Using Eq. 4.26a, it is possible to write

If ergodicity is assumed, then the PSDFs & cross
PSDFs of derivatives of the process may be easily
derived using equations 4.51 and 4.58.

o T
Contd.
} }
T

2
2 2
x p
0
0
1
x(t ) dt =r = h( )S d (4.56)
T
} }

2
x p
0 0
2
x p
*
x p
S( )d= h()S d (4.57)
S( )= h()S (4.58)
S( )= h()S h() (4.59)
2/4
T.K. Datta
( ) ( )
( ) ( )
( )
( )
-
-
2
x x
xx x xx x
2
4
x x
2 2
xx x xx x
2
x x
4
x x
T
xx x xx x
T
2 2
xx x xx x
x =ix (4.60)
S = S (4.61)
S =iS S = -iS (4.62)
x = - x (4.63)
S = S (4.64)
S = - S S = - S (4.65)
S = S (4.66)
S = S (4.67)
S =iS ; S = iS (4.68)
S = - S ; S = - S (4.69a)
xx xx
S +S =0 (4.69b)
Contd.
2/5
T.K. Datta
Example 4.1: For the problem in example3.7, find
the rms value of the displacement;

Solution:
Digitized values of PSDF of Elcentro are given in
Appendix 4A(book)

can be obtained using above
equations.

0
= 12.24 rad/s ;
= 0.209 rad/s
Contd.
2 2 -1
n n
2
x p
h( )=( - +2i ) (4.51c)
S( )= h()S (4.58)
X
h(w ) & S
2/6
T.K. Datta
Contd.
PSDF of Elcentro earthquake, absolute square of
and PSDF of displacements are shown in the
Figs 4.8-4.10 .

h( )
0 20 40 60 80 100 120 140 160
0
0.005
0.01
0.015
0.02
Frequency (rad/sec)
P
S
D
F

o
f

a
c
c
e
l
e
r
a
t
i
o
n

(
m
2

s
e
c

3
/
r
a
d

)

Fig 4.8
2/7
T.K. Datta
Contd.
0 4 8 12 16 20 24
0
2
4
6
8 x 10
-4
Frequency (rad/sec)
|
h
(
w
)
|

2

0 5 10 15 20 25
0
2
4
6
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d

8 x 10
-4
Fig 4.10
Fig 4.9
2/8
T.K. Datta
Single point excitation, P(t) is given by

Using Eqns.4.35 & 4.71, following equation can be
written

Using Eqns.4.35 & 4.72

( ) ( ) ( )
g
P(t ) = -MI x (4.70)
x =H P (4.71)
MDOF system
( ) ( )
*T
xx pp
S =H S H (4.72)
(4.74)
g
T T
pp x
S =MII M S
2/9
(4.75)
g
T T *T
xx
x
S =HM II M H S
g g
x x
S =- HMIS (4.76)
x
T.K. Datta
Example 4.2 : For example 3.8, find PSDFs of the
displacement & for the same excitations
at all supports.
Solution:

1
u
2
u
Contd.
(
(

( (
( (

(
(

2 -1
T
1 2
1 0
M= m
0 2
1 0 3 -3
C=0.816 m+ 0.0027 k
0 2 -3 9
3 -3
K = k
-3 9
H=[K- M +iC]
k
=100; I = { 1 1}
m
=12.25rad/s; = 24.49rad/s
2/10
T.K. Datta
Using Eqn.4.75, is obtained; PSDFs of &
are shown in Fig.4.11
XX
S
Contd.
1
u
2
u
0 5 10 15 20 25
0
0.2
0.4
0.6
0.8
0.1
1.2
1.4
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

(
1
0
-
4
)

0 5 10 15 20 25
0
0.5
1
1.5
2
2.5
3
3.5
Frequency (rad/sec)
-

For u
1
For u
2
Fig 4.11
2/11
u1
u2
= 0.0154m
= 0.0078m
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

(
1
0
-
5
)

T.K. Datta
Contd.
For multipoint excitation:
g g
g g
T T *T
x x x
x x x
S =HMrS r M H (4.77)
S = -HMrS (4.78)
g
x
S is of size s x s; r is of size n x s
If all displacements are not required, then a reduced
is used of size m x n & is given by
H( )
XX
S
g
T T *T
xx mn x nm
S =H MrS r M H ( 4.79)
Without the assumption of ergodicity, Eqns 4.75-
4.78 can be derived (1-3).
3/1
T.K. Datta
Contd.
Example4.2: (a) For example 4.2, if a time lag of 5s is
introduced between supports, find the PSDFs of u
1
& u
2

; b) For example 3.9, find PSDFs of the degrees of
freedom 4 & 5 for correlated and partially correlated
excitations (with time lag 5s).
3/2
Solution: For example 4.2
(
(

| |
|
|
\ .
(
| | | |
(
| |
(
\ . \ .
(

ij
s
1 2
xg 1 1 xg 1 2
2 1
1 1 1
1
r =
1 1 1 3
r
coh(i, j) = exp -
2v
1
5 10
S = 1 S = exp - = exp -
2 2
1
PSDFs & cross PSDFs are shown in Fig4.12 (a-d)
T.K. Datta
Contd.
0 5 10 15 20 25
0
1
2
3
4
5
x 10
-5
Frequency (rad/sec)
0 5 10 15 20 25 30
0
0.2
0.4
0.6
0.8
1
1.2
x 10
-5
Frequency (rad/sec)
Displacement u
1
Displacement u
2
Fig 4.12
3/3

Rms values of u
1
& u
2
are 0.0089m (0.0092m) &
0.0045m (0.0048m)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

T.K. Datta
3/4
0 5 10 15 20 25
0
1
2
3
4
5
x 10
-5
Frequency (rad/sec)
0 5 10 15 20 25 30
0
0.2
0.4
0.6
0.8
1
1.2
x 10
-5
Frequency (rad/sec)
Displacement u
1
Displacement u
2
Contd.
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

T.K. Datta
For the problem of example 3.9, required matrices
& values of other parameters are given below:

3/5
1
5.58rad/s e =
2
18.91rad/s e =
(
(

3
19.56 10.5
EI
K=
10.5 129 L
3
EI
= 2
mL
=0.431
=0.004
(
(

0.479 0.331
r =
-0.131 0.146
C=M+K
(
(

2.5 1.67
M= m
1.67 2.5
Using Eq 4.77, PSDFs are obtained & are
shown in Figs.4.13 & 4.14.
T.K. Datta
Contd.
Rms values for d.o.f 4 & 5 are
0.0237(corr.)& 0.0168(partially corr.)
0.0005(corr.) & 0.0008(partially corr.)
Fig 4.13
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
x 10
-4
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

0 5 10 15 20 25 30
0
0.5
1
1.5
2
3
3.5
x 10
-4
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

Without time lag
With time lag
3/6
T.K. Datta
Contd.
0 2 4 6 8 10 12 14 16 18 20
0
1
2
3
4
x 10
-7
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

0 5 10 15 20 25 30
0
0.5
1
1.5
2
x 10
-7
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

Without time lag
With time lag
Fig 4.14
3/7
T.K. Datta
PSDFs of absolute displacements
Absolute displacement is obtained by adding
ground displacement to the relative displacement

PSDF of is obtained using Eqn. 4.37

Example 4.4: For example 4.3, find the PSDFs of
absolute displacement of d.o.f 4 & 5.
Solution: Let & represent

x =Ix +rx (4.80)
a g
a
x
( ) ( ) ( )
a g g g
g g g g
T T T
x xx x xx x x
2
g g
2 T
x x x xx x x
S =S +rS r +IS r +rS I (4.81)
x = -HMrx =HMr x (4.82)
S =HMr S and S =S (4.83)
x
g
x
| |
(

T T
4 5 g g1 g2
x = x x x = x x
3/8
T.K. Datta
Contd.
Using Eqn. 4.83

Using Eqn. 4.81, is obtained.

The PSDFs of & are shown in Figs 4.15
(a-b). rms values are given as 0.052m & 0.015m
respectively.

(
(

(
(
(

g g g
g g
g1 4 g2 4
g
g1 5 g2 5
2 -2
x x x x
11 21
x x ij
12 22
x x x x
x x
x x x x
S =HMr S =HMr S (4.84)
c c
S = S c =coh(i, j) (4.85)
c c
S S
S = (4.86)
S S
xa
S
4 x a
S
5 x a
S
3/9
T.K. Datta
Contd.
0 2 4 6 8 10 12 14 16 18 20
0
0.2
0.4
0.6
0.8
1
1.2
x 10
-3
Frequency (rad/sec)
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
x 10
-5
Frequency (rad/sec)
For d. o. f. 4
For d. o. f. 5
Fig 4.15
3/10
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2
s
e
c
/
r
a
d
)

T.K. Datta
PSDF of member forces
Consider the frame in Fig 3.7; x is the vector of
dyn. d.o.f. & as that of the condensed out d.o.f.

Consider column i-j; displacement at the ends of
column are

PSDF matrix of the member end forces are

T
xx
T
x xx x x
= Ax (4.87)
S = AS A (4.88)
S = AS & S =S (4.89)
(

T
i i j j
= x x (4.90)
f =K (4.91)
T
ff
S =KS K (4.92)
4/1
T.K. Datta
Contd.
If are in local coordinates, then

Example 4.5 : For the example 3.10, find PSDFs of
displacemens1 & 2; also find the PSDF of bending
moment at the centre.
Solution:

o
T T T
ff
= T (4.93)
S =KS K =KTS T K (4.94)
( (
( (
( (
( (

1 2 3
56 -16 8 0.813 -0.035 0.017
K = -16 80 -16 m C= -0.035 0.952 -0.035 m
8 -16 56 0.017 -0.035 0.811
=8.0rad/s; =9.8rad/s and =12.0rad/s
4/2
T.K. Datta
Following the same procedure , PSDFs of 1& 2
are obtained and are shown in Fig4.16(a-b).

For finding PSDF of bending moment, at the
center is required

& are zero as is zero at the center.

Displacement vector is

Contd.
u
| |
| |
T
1 2 3
x = x x x
3
= -1 0 1 x = Ax
4L
S
x
S

| |
T
2
1 1 2
= x , ,x ,
4/3
T.K. Datta
Contd.
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
x 10
-3
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

Fig 4.16 (a-b)
4/4
T.K. Datta
Contd.
Using modified stiffness for pinned end,
is eliminated ; are abs.displacements.

PSDF of bending moment obtained using Eqn.
4.92 is shown in Fig 4.16c. rms values of
are 0.0637m, 0.1192m & 1.104m .

1
1 2
x &x
1 2
x , x & B.M.
4/5
0 2 4 6 8 10 12 14 16 18 20
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Frequency (rad/sec)
P
S
D
F

o
f

B
.
M
.

x

m
a
s
s

m
(
'
g
'
m
)
2
s
e
c
/
r
a
d
)

Fig 4.16(c)
T.K. Datta
Modal spectral analysis
Advantages of modal analysis have been
described before.

For multipoint excitation, the i
th
modal equation
can be written as

r is the influence coefficient matrix of size mxn.

h
i
(w) for each modal equation can be easily
obtained.

2 T
i i i i i i i i i i g
T
2
i
i i i i i i g i
i
T
i i i
mz +2 mz +m z =-j Mrx (4.95)
-j Mr
z +2 z + z = x =p i =1.....r (4.96)
m
m = j Mj
4/6
T.K. Datta
i
()
i
p( ) can be related to by
Contd.
( ) ( ) ( )
( )
( )
i i i
T
i g
i
i
z =h p i =1.....r (4.97a)
-j Mrx
p = (4.97b)
m
Elements of PSDF matrix of z are given by
i j g
*
i j T T T
z z i x j
i j
h h
S = j MrS r M j i =1....r, j =1....r (4.98)
mm
Using modal transformation rule
T
xx zz
x=z
S = S (4.99)
is mr
4/7
T.K. Datta
Contd.
Example 4.6: For problem example 3.11,find PSDF of
d.o.f 1(tower top) and d.o.f 2(centre of deck). It is
assumed that a uniform time lag of 5s between the
supports exists.

684 0 149 20 0 0
0 684 149 , 0 20 0
149 149 575 0 0 60
m m
( (
( (
= =
( (
( (

K M
0.781 0.003 0.002 0.218
0.218 0.002 0.003 0.781
0.147 0.009 0.0009 0.147

(
(
=
(
(

r
| |
| |
| |
1 2 3
2.86rad/s; 5.85rad/s ; 5.97rad/s
0.036 0.036 0.125
0.158 0.158 0
0.154 0.154 0.030
T
T
T
e e e = = =
=
=
=
1
2
3
|
|
|
Solution
4/8
T.K. Datta
Contd.
rms values of displacement for d.o.f 1 & 2
are:
rms modal direct
d.o.f1 0.021m 0.021m
d.o.f2 0.015m 0.015m
value
PSDFs are calculated using equations 4.98-
4.99 and shown in Fig 4.17 a-c.
4/9
It is seen that the values obtained by modal and
direct analyses are the same because the number
of modes taken are equal to the number of d.o.f.
(ie all modes are considered).

T.K. Datta
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
x 10
-4
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

0 5 10 15 20 25 30 35 40 45 50
-6
-4
-2
0
2
4
x 10
-5
Frequency (rad/sec)
Real Part
C
r
o
s
s

P
S
D
F

b
e
t
w
e
e
n

u
1

a
n
d

u
2

(
m
2

s
e
c
/
r
a
d
)

Fig 4.17b
4/10
Contd.
Fig 4.17a
T.K. Datta
Contd.
4/11
0 5 10 15 20 25 30 35 40
-1
0
1
2
3
x 10
-20
Frequency (rad/sec)
Imaginary Part
C
r
o
s
s

P
S
D
F

b
e
t
w
e
e
n

u
1

a
n
d

u
2

(
m
2

s
e
c
/
r
a
d
)

Fig 4.17c
T.K. Datta
4/12
0 1 2 3 4 5 6 7 8 9 10
0
1
x 10
-4
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
x 10
-4
Frequency (rad/sec)
P
S
D
F

o
f

d
i
s
p
l
a
c
e
m
e
n
t

(
m
2

s
e
c
/
r
a
d
)

Top of the left tower
Centre of the deck
Contd.
Fig 4.18
T.K. Datta
Spectral analysis (state space)
When state space equation is used, is obtained
as:
(

g g
*T
zz f f
-1
S =HS H (100a)
H= I- A (100b)
zz
S
g g
f f
S
is the PSDF matrix of vector.

contains and terms; addition of these
two terms becomes zero.

For modal spectral analysis, eigen values &
eigen vector of matrix A are obtained.

Same equations as used before are utilized to
find PSDF of responses.

g
f
xx xx
S +S =0
xx
S
xx
S
zz
S
4/13
T.K. Datta
Contd.
Example4.7: For the exercise problem 3.12, find the
PSDF matrices of top & first floor of displacements;
ground motion is perfectly correlated.

0.0 0.0 0.0 0.0 1 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 1 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 1 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 1
2.0 1.0 0.0 0.0 1.454 0.567 0.0 0.0
2.0 2.0 1.0 0.0 1.134 1.495 0.567 0.0
0.0 1.0 3.0 2.0 0.0 0.567 2.062 1.134
0.0 0.0 2.0 4.0 0.0
=

A
0.0 1.134 2.630
(
(
(
(
(
(
(
(
(
(
(
(

Using eqns 4.100(a-b), PSDFs are calculated
and are shown in fig.4.19.
4/14
Solution
T.K. Datta
Contd.
rms values are as below:
rms modal direct statespace
d.o.f1 0.0903m 0.0907m 0.0905m
d.o.f4 0.0263m 0.0259m 0.0264m
value
Steps for developing a program for spectral
analysis of structures with multi-support excitations
using MATLAB are given.

Steps cover all types of methods ie;modal , direct
and state space formulations.

The program can easily make use of the standard
MATLAB routines.
4/15
T.K. Datta
Lec-1/74

Seismic Analysis of Structures - II

Încărcat de

Informații document

Descriere originală:

Drepturi de autor

Formate disponibile

Partajați acest document

Partajați sau inserați document

Opțiuni de partajare

Vi se pare util acest document?

Este necorespunzător acest conținut?

Drepturi de autor:

Formate disponibile

Seismic Analysis of Structures - II

Încărcat de

Drepturi de autor:

Formate disponibile

T.K.

is the quasi static response for which

S-ar putea să vă placă și