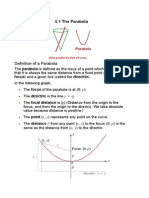
A parabola is the set of all points in a plane such that

each point in the set is equidistant from a line called

the directrix and a fixed point called the focus.
The Standard Form of a Parabola that opens to the right
and has a vertex at (0,0) is



px y 4
2
=
The Parabola that opens to the right and has a vertex at
(0,0) has the following characteristics

p is the distance from the vertex of the parabola to the
focus or directrix
This makes the coordinates of the focus (p,0)
This makes the equation of the directrix x = -p
The makes the axis of symmetry the x-axis (y = 0)
The Standard Form of a Parabola that opens to the left
and has a vertex at (0,0) is





px y 4
2
=
The Parabola that opens to the left and has a vertex at
(0,0) has the following characteristics

p is the distance from the vertex of the parabola to the
focus or directrix
This makes the coordinates of the focus(-p,0)
This makes the equation of the directrix x = p
The makes the axis of symmetry the x-axis (y = 0)


The Standard Form of a Parabola that opens up and
has a vertex at (0,0) is




py x 4
2
=
The Parabola that opens up and has a vertex at (0,0) has
the following characteristics

p is the distance from the vertex of the parabola to the
focus or directrix
This makes the coordinates of the focus (0,p)
This makes the equation of the directrix y = -p
This makes the axis of symmetry the y-axis (x = 0)
The Standard Form of a Parabola that opens down and
has a vertex at (0,0) is



py x 4
2
=
1999 Addison Wesley Longman, Inc.
The Parabola that opens down and has a vertex at (0,0)
has the following characteristics

p is the distance from the vertex of the parabola to the
focus or directrix
This makes the coordinates of the focus (0,-p)
This makes the equation of the directrix y = p
This makes the axis of symmetry the y-axis (x = 0)
The Standard Form of a Parabola that opens to the right
and has a vertex at (h,k) is






) ( 4 ) (
2
h x p k y =
The Parabola that opens to the right and has a vertex at
(h,k) has the following characteristics..

p is the distance from the vertex of the parabola to the
focus or directrix
This makes the coordinates of the focus (h+p, k)
This makes the equation of the directrix x = h p
This makes the axis of symmetry


a
b
y
2

=
The Standard Form of a Parabola that opens to the left
and has a vertex at (h,k) is




) ( 4 ) (
2
h x p k y =
The Parabola that opens to the left and has a vertex at
(h,k) has the following characteristics


p is the distance from the vertex of the parabola to the
focus or directrix
This makes the coordinates of the focus (h p, k)
This makes the equation of the directrix x = h + p
The makes the axis of symmetry

a
b
y
2

=
The Standard Form of a Parabola that opens up and has
a vertex at (h,k) is



) ( 4 ) (
2
k y p h x =
The Parabola that opens up and has a vertex at (h,k) has
the following characteristics

p is the distance from the vertex of the parabola to the
focus or directrix
This makes the coordinates of the focus (h , k + p)
This makes the equation of the directrix y = k p

The makes the axis of symmetry

a
b
x
2

=
The Standard Form of a Parabola that opens down and
has a vertex at (h,k) is




) ( 4 ) (
2
k y p h x =
Copyright 1999-2004 Oswego City School District Regents Exam Prep Center
The Parabola that opens down and has a vertex at (h,k) has the
following characteristics


p is the distance from the vertex of the parabola to the focus or
directrix
This makes the coordinates of the focus (h , k - p)
This makes the equation of the directrix y = k + p

This makes the axis of symmetry
a
b
x
2

=
The huge chimney of a nuclear power plant has the shape of a hyperboloid, as does
the architecture of the James S. McDonnell Planetarium of the St. Louis Science Center.
Jill Britton, September 25, 2003
The set of all points in the plane, the difference of
whose distances from two fixed points, called the
foci, remains constant.

A sonic boom shock wave has the
shape of a cone, and it intersects the
ground in part of a hyperbola. It hits
every point on this curve at the same
time, so that people in different places
along the curve on the ground hear it at
the same time. Because the airplane is
moving forward, the hyperbolic curve
moves forward and eventually the boom
can be heard by everyone in its path.
General Rules
x and y are both squared
Equation always equals(=) 1
Equation is always minus(-)
a
2
is always the first denominator
c
2
= a
2
+ b
2
c is the distance from the center to each foci on the major
axis
a is the distance from the center to each vertex on the major
axis


General Rules
b is the distance from the center to each midpoint of the
rectangle used to draw the asymptotes. This distance runs
perpendicular to the distance (a).
Major axis has a length of 2a
Eccentricity(e): e = c/a (The closer e gets to 1, the closer it is
to being circular
If x
2
is first then the hyperbola is horizontal
If y
2
is first then the hyperbola is vertical.


General Rules
The center is in the middle of the 2 vertices and the 2
foci.
The vertices and the covertices are used to draw the
rectangles that form the asymptotes.
The vertices and the covertices are the midpoints of
the rectangle
The covertices are not labeled on the hyperbola
because they are not actually part of the graph

The standard form of the Hyperbola with a center at
(0,0) and a horizontal axis is




1
2
2
2
2
=
b
y
a
x
The Hyperbola with a center at (0,0) and a horizontal
axis has the following characteristics


Vertices ( a,0)
Foci ( c,0)

Asymptotes:
x
a
b
y =

The standard form of the Hyperbola with a center at

(0,0) and a vertical axis is




1
2
2
2
2
=
b
x
a
y
The Hyperbola with a center at (0,0) and a vertical
axis has the following characteristics


Vertices (0, a)
Foci ( 0, c)

Asymptotes:
x
b
a
y =

The standard form of the Hyperbola with a center at

(h,k) and a horizontal axis is




1
) ( ) (
2
2
2
2
=

b
k y
a
h x
The Hyperbola with a center at (h,k) and a horizontal
axis has the following characteristics


Vertices (h a, k)
Foci (h c, k )

Asymptotes:
) ( h x
a
b
k y =

The standard form of the Hyperbola with a center at

(h,k) and a vertical axis is




1
) ( ) (
2
2
2
2
=

b
h x
a
k y
The Hyperbola with a center at (h,k) and a vertical
axis has the following characteristics

Vertices (h, k a)
Foci (h, k c)

Asymptotes:
) ( h x
b
a
k y =

0
2 2
= + + + + + F Ey Dx Cy Bxy Ax
o o sin ' cos ' y x x =
o o cos ' sin ' y x y + =
B
C A
= o 2 cot
C A
B

= o 2 tan
or
The set of all points in a plane that are the same
distance from a given point called the focus and a
given line called the directrix.
3.5
3
2.5
2
1.5
DIRECTRIX
FOCUS
Same Distance!
POINT
GOAL: Turn
2
into y ax bx c = + +
2
( ) y a x h k = +
1. Start with
2. Group the two x-terms
3. Pull out the constant with x
2
from the grouping
4. Complete the square of the grouping
**Look back to Topic 6.3 for help**
5. Write the squared term as subtraction so that you end
with
2
y ax bx c = + +
2
( ) y a x h k = +
**Remember that whatever you add in the
grouping must be subtracted from the c-value**
Group x-terms
Pull out GCF
Complete the Square
Factor and simplify
4 )) 2 ( ( 3
2
+ = x y
or 4 ) 2 ( 3
2
+ + = x y
12 16 ) 4 4 ( 3
2
+ + + = x x y
____ 16 ___) 4 ( 3
2
+ + + = x x y
16 ) 4 ( 3
2
+ + = x x y
16 ) 12 3 (
2
+ + = x x y
16 12 3 :
2
+ + = x x y Example
1
,
4
h k
a
| |
+
|
\ .
Equation
Axis of symmetry
x = h y = k
Vertex
(h, k) (h, k)
Focus
Directrix
Direction of opening Up: a>0, Down: a<0 Right: a>0, Left: a<0
Latus Rectum

2
( ) y a x h k = +
2
( ) x a y k h = +
1
,
4
h k
a
| |
+
|
\ .
1
4
y k
a
=
1
4
x h
a
=
1
units
a
1
units
a
2
3( ( 2)) 4 y x = +
length of latus rectum:
1
12
directrix: y =
47
12
axis of symmetry: x = -2
vertex: (-2,4)
focus: (-2,
49
12
)
Write the following equation in parabolic form. State the
vertex, axis of symmetry and direction of opening.
2
10 7 x y y =
2
Parabolic form: ( 5) 32 x y =
Vertex: (5, -32)
Axis of symmetry: 5 x =
Direction of Opening: upward
Ken Youssefi Mechanical Engineering Dept. 43
Conic curves or conics are the curves formed by the intersection of a plane
with a right circular cone (parabola, hyperbola and sphere).
A parabola is the curve created when a plane intersects a right circular
cone parallel to the side (elements) of the cone
Cutting plane

Parallel
Ken Youssefi Mechanical Engineering Dept. 44
A hyperbola is the curve created when a plane parallel to the axis and
perpendicular to the base intersects a right circular cone.
Element
(side)
Hyperbola
Orthographic view
A hyperbola is a set of points in a plane the difference of whose distances from two
fixed points, called foci, is a constant.
F
1
F
2
d
1
d
2
P

For any point P that is on the
hyperbola, d
2
d
1
is always the same.
In this example, the origin is the
center of the hyperbola. It is midway
between the foci.
F

F

V V
C
A line through the foci intersects the
hyperbola at two points, called the
vertices.
The segment connecting the vertices
is called the transverse axis of the
hyperbola.
The center of the hyperbola is located
at the midpoint of the transverse
axis.
As x and y get larger the branches of the hyperbola approach a pair of
intersecting lines called the asymptotes of the hyperbola. These
asymptotes pass through the center of the hyperbola.
F

F

V
V
C
The figure at the left is an example
of a hyperbola whose branches
open up and down instead of right
and left.
Since the transverse axis is
vertical, this type of hyperbola
is often referred to as a
vertical hyperbola.
When the transverse axis is
horizontal, the hyperbola is
referred to as a horizontal
hyperbola.
(x h)
2
(y k)
2
a
2
b
2
Horizontal
Hyperbola
(y k)
2
(x h)
2
b
2
a
2
= 1
Vertical
Hyperbola
= 1
The center of a hyperbola is at the point (h, k) in either form
For either hyperbola, c
2
= a
2
+ b
2
Where c is the distance from the center to a focus point.

The equations of the asymptotes are

y = (x h) + k
and
y = (x h) + k
ba
ba -
A parabola is a set of points in a plane that are equidistant from a fixed line, the
directrix, and a fixed point, the focus.
For any point Q that is on the
parabola, d
2
= d
1

Directrix
Focus
Q
d
1
d
2
The latus rectum of a parabola is a
line segment that passes through the
focus, is parallel to the directrix and
has its endpoints on the parabola.
The length of the latus rectum is |4p|
where p is the distance from the
vertex to the focus.
V
Things you should already know
about a parabola.
Forms of equations
y = a(x h)
2
+ k
opens up if a is positive
opens down if a is negative
vertex is (h, k)
y = ax
2
+ bx + c
opens up if a is positive
opens down if a is negative
vertex is , f( )
-b
2a
-b
2a
Thus far in this course we have studied parabolas that are vertical - that is,
they open up or down and the axis of symmetry is vertical
In this unit we will also study
parabolas that are horizontal that
is, they open right or left and the
axis of symmetry is horizontal
In these equations it is the y-
variable that is squared.
V
x = a(y k)
2
+ h
x = ay
2
+ by + c
or
Horizontal
Hyperbola
Vertical
Hyperbola
If a > 0, opens right

If a < 0, opens left

The directrix is vertical

x = ay
2
+ by + c
y = ax
2
+ bx + c
Vertex: x =
If a > 0, opens up

If a < 0, opens down

The directrix is horizontal

Remember: |p| is the distance from the vertex to the focus
vertex:
-b
2a
y =
-b
2a
a =
1
4p
the directrix is the same distance from the vertex as the focus is
A hyperbola is created from the intersection of a
plane with a double cone.
A hyperbola is defined by a group of points that
have a same difference of distance from two foci.
When you subtract the small line from the long
line for each ordered pair the remaining value is
the same.
Hyperbolas can be
symmetrical around the x-
axis or the y-axis The one
on the right is symmetrical
around the x-axis.
A hyperbola is a set of points in a plane the difference of whose distances from two
fixed points, called foci, is a constant.
F
1
F
2
d
1
d
2
P

For any point P that is on the
hyperbola, d
2
d
1
is always the same.
In this example, the origin is the
center of the hyperbola. It is midway
between the foci.
F

F

V V
C
A line through the foci intersects the
hyperbola at two points, called the
vertices.
The segment connecting the vertices
is called the transverse axis of the
hyperbola.
The center of the hyperbola is located
at the midpoint of the transverse
axis.
As x and y get larger the branches of the hyperbola approach a pair of
intersecting lines called the asymptotes of the hyperbola. These
asymptotes pass through the center of the hyperbola.
F

F

V
V
C
The figure at the left is an example
of a hyperbola whose branches
open up and down instead of right
and left.
Since the transverse axis is
vertical, this type of hyperbola
is often referred to as a
vertical hyperbola.
When the transverse axis is
horizontal, the hyperbola is
referred to as a horizontal
hyperbola.