Logic and Sequential Circuit Design

(EC 201)


Textbook


Digital Logic and Computer Design by M.
Morris Mano (Jan 2000 )
Topics
Boolean Algebra and Logic Gates: Binary Logic and
Gates, Boolean Algebra and Functions, Canonical
and Standard Forms, Logic Operations, Digital Logic
Gates, and IC Digital Families.
Simplification of Boolean Functions: K-Map
Method and Simplification using Different Variables
Map, Simplification of Product of Sums,
Implementation with NAND and NOR Gates, Dont
Care Conditions, The Tabulation Method,
Determination of Prime-Implicants, and Selection
of Prime-Implicants.

Continue
Combinational Logic Design: Design Procedure,
Adders, Subtractors, Code Conversion, Analysis
Procedure, Multilevel NAND Circuits, Multilevel
NOR Circuits, Exclusive-OR, and Equivalence
Functions
Combinational Logic with MSI and LSI: Decimal
Adder, Magnitude Comparator, Decoders,
Encoders, Multiplexers, Demultiplexers, Binary
Adders, Binary Subtraction, Binary Adder-
Subtractors, Binary Multipliers and HDL
Representation VHDL/Verilog

Continue
Sequential Logic/Circuits: Latches, Flip-Flops,
Triggering of Flip-Flops, Clocked Sequential Circuits
and their Analysis, State Reduction and Assignment,
Flip-Flop Excitation Tables, Design Procedure,
Designing with D & JK Flip-Flops, HDL/Verilog
Representation for a Sequential Circuits
VHDL/Verilog
Boolean Algebra
&
Logic Gates
Common Postulates (Boolean Algebra)
Closure
N=,1,2,3,4,5,..-
It is closed w.r.t +
i.e. a+b=c
as a,b,cN
Associative Law
(x*y)*z = x*(y*z)
for all x,y,z,S
Commutative Law
x*y = y*x for all x,yS
x+y = y+x

x+y = y+x
x.Y = y.x
Common Postulates (Boolean Algebra)
Identity Element
e*x = x*e = x x S
e+x = x+e = x
0+x = x+0 = x
1*x = x*1 = x
Inverse
x*y = e a*1/a = 1
x+y = e
a+(-a) = 0
Distributed Law
x*(y.z) = (x*y) . (x*z)
x.(y+z) = (x.y) + (x.z)
x+(y.z) = (x+y) . (x+z)
x+0 = 0+x = x
x.1 = 1.x = x
x+x = 1
x.x = 0
Boolean Algebra and Logic Gates
x y x.y x y x+y x x
0 0 0 0 0 0 0 1
0 1 0 0 1 1 1 0
1 0 0 1 0 1
1 1 1 1 1 1
x y z Y+z x.(y+z) x.y x.z (x.y)+x.z
0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0
1 0 0 0 0 0 0 0
1 0 1 1 1 0 1 1
1 1 0 1 1 1 0 1
1 1 1 1 1 1 1 1
x.(y+z) = (x.y)+(x.z)
Postulates and Theorems of Boolean Algebra
Postulate 2 (a) x+0 = x (b) x.1 = x
Postulate 5 (a) x+x = 1 (b) x.x = 0
Theorem 1 (a) x+x = x (b) x.x = x
Theorem 2 (a) x+1 = 1 (b) x.0 = 0
Theorem3, involution (x) = x
Postulate3, commutative (a) x+y = y+x (b) xy = yx
Theorem4, associative (a) x+(y+z)=(x+y)+z (b) x(yz) = (xy)z
Postulate4, distributive (a) x(y+z)=xy+xz (b) x+yz = (x+y)(x+z)
Theorem5, DeMorgan (a) (x+y) = xy (b) (xy) = x+y
Theorem6, absorption (a) x+xy = x (b) x(x+y)=x
Theorems
1a. x+x = x
x+x = (x+x).1
= (x+x)(x+x)
= x+xx
=x+0
=x
1b. x.x = x (Remember Duality of 1a)
x.x = xx+0
= xx+xx
= x(x+x)
= x.1
=x
Theorems
2a. x+1 = 1
x+1 =1.(x+1)
= (x+x)(x+1)
= (x+x)
= x+x
= 1
2b. X.0 = 0 (Remember Duality of
of 2a)
3. (x) = x
Complement of x = x
Complement of x = (x) = x
6a x+xy = x
x+xy = x.1+xy
= x(1+y)
= x.1
=x
6b. x(x+y) = x (Remember Duality of 6a)

Can also be proved using truth table method

x y xy x+xy
0 0 0 0
0 1 0 0
1 0 0 1
1 1 1 1
x y x+y (x+y) x y xy
0 0 0 1 1 1 1
0 1 1 0 1 0 0
1 0 1 0 0 1 0
1 1 1 0 0 0 0
x=x+xy
(x+y) = xy DeMorgans Theorem
(xy) = x +y DeMorgans Theorem
Operator Precedence
1.( )
2.NOT
3.AND
4.OR
x
y
xy xy xy
x
y
x
y
z
x+(y+z)
x
y
z
xy+xz
VENN DIAGRAM FOR TWO VARIABLES
VENN DIAGRAM ILLUSTRATION X=XY+X
VENN DIAGRAM ILLUSTRATION OF THE DISTRIBUTIVE LAW
xy
x
y
TRUTH TABLE FOR F
1
=xyz, F
2
=x+yz, F
3
=xyz+xyz+xy and F
4
=xy+xz
x y z F1 F2 F3 F4
0 0 0 0 0 0 0
0 0 1 0 1 1 1
0 1 0 0 0 0 0
0 1 1 0 0 1 1
1 0 0 0 1 1 1
1 0 1 0 1 1 1
1 1 0 1 1 0 0
1 1 1 0 1 0 0
x
y
z
F1
z
y
F2
x
(a) F1 = xyz
(b) F2 = x+yz
(c) F3 = xyz+xyz+xy
F3
z
y
x
(c) F4 = xy+xz
F4
z
y
x
Implementation of Boolean Function with GATES
Algebraic Manipulations for Minimization of Boolean Functions
(Literal minimization)
1. x+xy = (x+x)(x+y)
= 1.(x+y)=x+y
2. x(x+y) = xx+xy
= 0+xy=xy
3. xyz+xyz+xy
= xz(y+y)+xy
= xz+xy
4. xy+xz+yz (Consensus Theorem)
=xy+xz+yz(x+x)
=xy+xz+xyz+xyz
=xy(1+z)+xz(1+y)
=xy+xz
5. (x+y)(x+z)(y+z)=(x+y)(x+z)
by duality from function 4
Complement of a Function
(A+B+C) = (A+X)
= AX
= A.(B+C)
= A.(BC)
= ABC
(A+B+C+D+..Z) = ABCD..Z
(ABCD.Z) = A+B+C+D+.+Z
Example using De Morgans Theorem (Method-1)
F1 = xyz+xyz
F1 = (xyz+xyz)
= (x+y+z)(x+y+z)
F2 = x(yz+yz)
F2= *x(yz+yz)+
= x+(y+z)(y+z)
Example using dual and complement of each
literal (Method-2)
F1 = xyz + xyz
Dual of F1 = (x+y+z)(x+y+z)
Complement F1 = (x+y+z)(x+y+z)

F2 = x(yz+yz)
Dual of F2=x+*(y+z)(y+z+
Complement =F2= x+ (y+z)(y+z)
Minterm or a Standard Product
n variables forming an AND term provide 2
n
possible
combinations, called minterms or standard products
(denoted as m1, m2 etc.).
Variable primed if a bit is 0
Variable unprimed if a bit is 1
Maxterm or a Standard Sum
n variables forming an OR term provide 2
n
possible
combinations, called maxterms or standard sums
(denoted as M1,M2 etc.).
Variable primed if a bit is 1
Variable unprimed if a bit is 0
MINTERMS AND MAXTERMS FOR THREE BINARY VARIABLES
MINTERMS MAXTERMS
x y z Term Designation Term Designation
0 0 0 xyz m0 x+y+z M0
0 0 1 xyz m1 x+y+z M1
0 1 0 xyz m2 x+y+z M2
0 1 1 xyz m3 x+y+z M3
1 0 0 xyz m4 x+y+z M4
1 0 1 xyz m5 x+y+z M5
1 1 0 xyz m6 x+y+z M6
1 1 1 xyz m7 x+y+z M7
FUNCTION OF THREE VARIABLES
x y z Function f1 Function f2
0 0 0 0 0
0 0 1 1 0
0 1 0 0 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
f1 = xyz+xyz+xyz =m1 + m4 + m7
f2 = xyz+xyz+xyz+xyz = m3 + m5 + m6 + m7
MINTERMS AND MAXTERMS FOR THREE BINARY VARIABLES

f1 = xyz+xyz+xyz
f1 = xyz+xyz+xyz+xyz+xyz
f1 =(x+y+z)(x+y+z)(x+y+z)(x+y+z) (x+y+z)
= M0.M2.M3.M5.M6
= M0M2M3M5M6
f2 = xyz+xyz+xyz+xyz
f2 = xyz+xyz+xyz+xyz
f2 = (x+y+z)(x+y+z)(x+y+z)(x+y+z)
= M0 M1 M2 M4
Canonical Form
Boolean functions expressed as a sum of minterms or product of
maxterms are said to be in canonical form.
M3+m5+m6+m7 or M0 M1 M2 M4
Sum of Minterms (Sum of Products)
Example: F = A+BC
F = A(B+B)+BC(A+A)
= AB+AB+ABC+ABC
= AB(C+C)+AB(C+C)+ABC+ABC
= ABC+ABC+ABC+ABC+ABC+ABC
= ABC+ABC+ABC+ABC+ABC
= m1+m4+m5+m6+m7
F(A,B,C)=E(1,4,5,6,7)


ORing of term AND terms of variables A,B &C
They are minterms of the function
Product of Maxterms (Product of sums)
Example: F = xy+xz
F = xy+xz
F = (xy+x)(xy+z) distr.law (x+yz)=(x+y)(x+z)
= (x+x)(y+x)(x+z)(y+z)
= (x+y)(x+z)(y+z)
= (x+y+zz)(x+z+yy)(y+z+xx)
= (x+y+z)(x+y+z)(x+z+y)(x+z+y)(y+z+x)(y+z+x)
= (x+y+z)(x+y+z)(x+y+z)(x+y+z)
= M0 M2 M4 M5
F(x,y,z) = H(0,2,4,5)


ANDing of terms Maxterms of the function (4 OR terms
of variables x,y&z)
Conversion between Canonical Forms
F(A,B,C) = E(1,4,5,6,7)
sum of minterms
F(A,B,C) = E(0,2,3)
= m0+m2+m3
F(A,B,C) = (m0+m2+m3)
= m0.m2.m3
= M0 M2 M3
= H(0,2,3)
Product of maxterms

Similarly
F(x,y,z) = H(0,2,4,5)
F(x,y,z) = E(1,3,6,7)

Standard Forms

Sum of Products (OR operations)
F1 = y+xy+xyz
(AND term/product term)

Product of Sums (AND operations)
F2=x(y+z)(x+y+z+w)


(OR term/sum term)
Non-standard form
F3=(AB+CD)(AB+CD)

Standard form of F3
F3=ABCD + ABCD

TRUTH TABLE FOR THE 16 FUNCTIONS OF TWO
BINARY VARIABLES


x y F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
Operator
symbols
+ ,
c
,

F0 = 0 F1 = xy F2 = xy F3 = x
F4 = xy F5 = y F6 = xy +xy F7= x +y
F8 = (x+y) F9 = xy +xy F10 = y F11 = x +y
F12 = x F13 = x + y F14 = (xy) F15 = 1



BOOLEAN EXPRESSIONS FOR THE 16 FUNCTIONS OF TWO VARIABLE

BOOLEAN OPERATOR NAME COMMENTS
FUNCTIONS SYMBOL

F0 =0 NULL BINARY CONSTANT 0

F1=xy x.y AND x and y

F2=xy x/y inhibition x but not y
F3=x transfer x
F4=xy y/x inhibition y but not x
F5=y transfer y
F6=xy+xy x y exclusive-OR x or y but not both
F7=x+y x+y OR x or y
F8=(x+y) x y NOR not OR
F9=xy+xy x y *equivalence x equals y
F10=y y complement not y
F11=x+y x c y implication if y then x
F12=x x complement not x
F13=x+y x y implication if x then y
F14=(xy) x y NAND not AND
F15=1 IDENTITY BINARY CONSTANT 1





*Equivalence is also known as equality, coincidence, and exclusive
NOR
16 logic operations are obtained from two variables x &y
Standard gates used in digital design are: complement, transfer, AND,
OR , NAND, NOR, XOR & XNOR (equivalence).
H and L LEVEL IN IC LOGIC FAMILIES

IC Family Voltage
Type Supply (V)
High-level voltage
(V)


Range Typical
Low-level
voltage (V)
TTL Vcc=5
ECL VEE=-5.2
CMOS VDD=3--10
Positive Logic:
Negative Logic

2.4-5 3.5
-0.95- -0.7 -0.8
VDD VDD
Logic-1
Logic-0

0-0.4 0.2
-1.9-- -1.6 -1.8
0-0.5 0
Logic-0
Logic-1

Range Typical
TYPICAL CHARACTERISTICS OF IC
LOGIC FAMILIES
IC Logic
Family
Fan out Power
Dissipation (mw)
Propagation
delay (ns)
Noise Margin (v)
Standard TTL
Shottky TTL
Low power
Shottky TTL
ECL
CMOS

10
10

20
25
50
10
22

2
25
0.1
10
3

10
2
25


0.4
0.4

0.4
0.2
3
TTL basic circuit : NAND gate
ECL basic circuit: NOR gate
CMOS basic circuit: Inverter to construct NAND/NOR
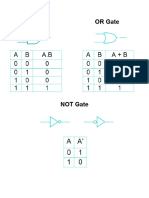
DIGITAL LOGIC GATES

NAME GRAPHIC
SYMBOL
ALGEBRIC
FUNCTION
TRUTH
TABLE
AND F=XY X Y F
0 0 0
0 1 0
1 0 0
1 1 1

OR F=X+Y X Y F
0 0 0
0 1 1
1 0 1
1 1 1

X
Y
F
Y
X
F
NAME GRAPHIC
SYMBOL
ALGEBRIC
FUNCTION
TRUTH
TABLE
Inverter

F=X
X F
0 1
1 0

Buffer

F=X
X F
0 0
1 1



NAND

F=(XY)
X Y F
0 0 1
0 1 1
1 0 1
1 1 0

X F
X F
X
F
Y
NAME GRAPHIC
SYMBOL
ALGEBRIC
FUNCTION
TRUTH
TABLE


NOR


F=(X+Y)
X Y F
0 0 1
0 1 0
1 0 0
1 1 0


Exclusive-OR
(XOR)

F=XY+XY
= X Y
X Y F
0 0 0
0 1 1
1 0 1
1 1 0

Exclusive-NOR
or
Equivalence


F=XY+XY
=X Y
X Y F
0 0 1
0 1 0
1 0 0
1 1 1
F
Y
X
X
F
Y
F
X
Y
Y
(X Y) Z=(X+Y) Z


Y
x
(X+Y)
=XZ+YZ
[Z+(X+Y)]
(Y+Z)
(X ( Y Z)=X(Y+ Z)


=XY+XZ
[X+(Y+Z)]
Z
X
Z
Demonstrating the nonassociativity of the NOR operator
(X + Y)+ Z = X +(Y+ Z)

X
Y
Z
(X+Y+Z)
X
Y
Z
(XYZ)
(a) There input NOR gate (b) There input NAND gate
A
B
C
D
E
F=[(ABC). (DE)]=ABC+DE
(c) Cascaded NAND gates
Multiple-input AND cascaded NOR and NAND gates
X
Y
Z
F=X Y Z
(a) Using two input gates
X
Y
Z
(b) Three input gates
(b) Three input exclusive OR gates
TRUTH TABLE
X Y Z F
0 0 0 0 1
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 0


XOR
XNOR
Odd
function
Even
function
F=X Y Z
IC DIGITAL LOGIC FAMILIES
TTL Transistor- Transistor Logic
Very popular logic family.
It has a extensive list of digital functions.
It has a large number of MSI and SSI devices, also has LSI devices.

ECL Emitter Coupled Logic
Used in systems requiring high speed operations.
It has a large number of MSI and SSI devices, also LSI devices.
MOS Metal-Oxide Semiconductor
Used in circuit requiring high component density
It has a large number of MSI and SSI devices, also LSI devices (mostly)
CMOS Complementary MOS
Used in systems requiring low power consumption.
It has a large number of MSI and SSI devices, also has LSI devices.
I
2
L Integrated - Injection Logic
Used in circuit requiring high component density.
Mostly used for LSI functions







1 2 3 4 5 6 7
14 13 12 11 10 9 8
VCC
GND
1 2 3 4 5 6 7
14 13 12 11 10 9 8
VCC
GND
Some Typical IC Gates
7400 Quadruple 2-input
NAND gates
7404 Hex Inverters
TTL gates
16 15 14 13 12 11 10 9
1 2 3 4 5 6 7 8
VCC 2
VEE 2 (-5.2V)
VCC 1
10107 Triple
Exclusive OR/
NOR gates
16 15 14 13 12 11 10 9
1 2 3 4 5 6 7 8
VCC 2
VCC 1
VEE (-5.2V)
10102 Quadruple
2-Input NOR gate
Some Typical IC Gates
1 2 3 4 5 6
NC
7
Vss (GND)
NC
8
9 10 11 12 13
VDD
14
(3-15 V)
C MOS
GATES
4002 dual 4 input NOR gates
NC
16
1
VDD
3 4 5 6 7 8 Vss
(GND)
9 10 11 12 14 15
2
(3-15 V)
4050 Hex buffer
CMOS
GATES
NC
13
0
1 H
L
0
1
H
L
LOGIC
VALUE
SIGNAL
VALUE
LOGIC
VALUE
SIGNAL
VALUE
Negative Logic
Positive Logic
Signal amplitude assignment and type of logic
X y z
L L H
L H H
H L H
H H L
TTL
7400
GATE
x
y
z
Gate block diagram

Gate block diagram

Truth table in terms of
H and L

X y z
0 0 1
0 1 1
1 0 1
1 1 0
Truth table for positive logic
H=1, L=0

x
y
z
Graphic symbol for
positive logic NAND gate
X y z
1 1 0
1 0 1
0 1 1
0 0 1
Truth table for negative logic
L=1 H=0

x
z
y
Graphic symbol for negative logic
NOR gate

+ive logic NAND or -ive logic NOR
+ive logic NOR or -ive logic NAND

Same gate can function
DEMONSTRATION OF POSITIVE AND
NEGATIVE LOGIC
Fan-out
Specifies the number of standard loads (the amount of current needed by an input
of another gate in the same IC family) that the output of a gate can drive without
impairing its normal operation. it is expressed by a number.
Power dissipation
It is the supplied power required to operate the gate. It is expressed in mw.
Propagation delay
It is the average transition delay time for a signal to propagate from input to
output when the binary signals change in value. It is expressed in ns.
Noise margin
It is the maximum noise voltage added to the input signal of a digital circuit that
does not cause an undesirable change in the circuit output. It is expressed in volts
(v).

Characteristics of IC logic families
(parameters)