1

3. Funciones anaIticas
2
Derivada de una funcin compleja
Teorema del valor medio para funciones reales Si I(x) es continua en a x b y I
'(x) existe para a x b, entonces hay al menos un punto c (a c b) tal que: I '(c)
| I(b) I(a) | / | b a |.
-1
1
0
Adems los dos
caminos tienen
longitudes diferentes.
inguno de los dos teoremas aplican a las Iunciones complejas.
Por ejemplo: el teorema del valor intermedio, nos dice que si I(a)
-1 y I(b) 1 entonces necesariamente existe al menos un valor
, a b, tal que I() = 0. En compleja, podemos empezar en -
1 y acabar en 1 sin haber pasado por (00i).
Teorema del valor intermedio para funciones reales
Sea I(x) continua para a x b y I(a) = I(b) entonces I toma todos los
valores entre I(a) y I(b) en el intervalo a b

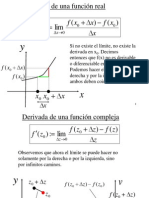
Derivada de una funcin real

x
y
0
x
x
x f x x f
x f
x
A
A +
=
'
A
) ( ) (
lim : ) (
0 0
0
0
x x A +
0
x A
) (
0
x f
) (
0
x x f A +
Si no existe el limite, no existe la
derivada en x
0
. Decimos
entonces que I(x) no es derivable
o no es diIerenciable en x
0
.
Podemos hacer el limite por la
derecha y por la izquierda, y
ambos deben coincidir.
x
y
0
:
:
: f : : f
: f
:
A
A +
=
'
A
) ( ) (
lim : ) (
0
0
0
: A
u
v
) (
0
: : f A +
) (
0
: f
) ( ) (
0 0
: f : : f A +
: : A +
0
Derivada de una funcin compleja
Observemos que ahora el limite se puede hacer no
solamente por la derecha o por la izquierda, sino
por inIinitos caminos. Para que la derivada este deIinida
el limite debe existir y ser el mismo independientemente
del camino.

ostrar que f(:) :

n
es diIerenciable para todo z y
que f
/
(:) n:
n-1
.
Efemplo.
1
0
1
0
1
0
0
1
0
0 0
0
0
0 0
0
0
) ( lim
) (
lim
) (
lim
) (
lim : ) (

=
A

=
A

=
A A
= A

'
+

'

=
A
A

'
+

'

=
A
A

'
+

'

=
A
A +
=
'

n i i n
n
i
:
i i n
n
i
:
n i i n
n
i
:
n n
:
n: : :
i
n
:
: :
i
n
:
: : :
i
n
:
: : :
: f
Observa que el resultado es independiente de la trayectoria
con que se aproxima a cero. Como :
0
es arbitrario, el
resultado es valido para todo : y f'(:) n:
n-1
.
: A

a reglas de derivabilidad son las mismas que en calculo

de Iunciones reales de variable real:
(c I)
/
c I
/
(Ig)
/
I
/
g
/
(I g)
/
I
/
g I g
/
(I/g)
/
(I
/
g - I g
/
)/g
2
a regla de la cadena rige de la misma Iorma.
Efercicio.
Demostrar las reglas a
partir de la deIinicion
de derivada.

#egla de L'Hpital:
Si I(z
0
) 0 y g(z
0
) 0 y las Iunciones son
diIerenciables en z
0
con g'(z
0
) diIerente de 0,
entonces:
) ( '
) ( '
lim
) (
) (
lim
0 0
: g
: f
: g
: f
: : : :
=
Extension: Si I(z
0
) I'(z
0
) ...
I
(n-1)
(z
0
) 0 y g(z
0
) g'(z
0
) ...
g
(n-1)
(z
0
) 0 y las Iunciones y
las 2n Iunciones derivadas son
diIerenciables en z
0
(y con
g
(n)
(z
0
) diIerente de cero),
entonces:
) (
) (
lim
) (
) (
lim
) (
) (
0 0
: g
: f
: g
: f
n
n
: : : :
=
uillaume Franois Antoine
Marquis de L'Hpital
(1671 - 1704)
10
Diferenciales
Si f(:) es continua y tiene primera derivada continua en una
region R, entonces:
:

/:
/
: f /: : f /
:
/: /: : f : : : f
:
A
A
= = =
A
+ = A + A = A
A 0
lim ) ( ' ) ( '
. 0 cuando 0 donde
) ( ' ) ( '
s
s s
DiIerencial de w
11
E8 falacia8.

veces
2
2
2
2
2


2 2 2
1 1
x
x x x + + =
+ + + =
+ + =
+ =
=
Derivando a ambos lados:
1 2
1 1 2
veces
=
= + + = x x
x


12
Algunas Iunciones reales no poseen derivada
(en ciertos puntos)...
Por ejemplo:
De Iorma similar, algunas Iunciones complejas
no poseen derivada. en ningun punto del plano
complejo!
Demostrado por Cauchy en 120
x
y
x
y
x
x f
1
) ( =
1
Fractales: Curva de Koch, copo de nieve o isla del diablo
Continuo en todos sus puntos pero no
diIerenciable en ninguno.Perimetro inIinito en un area Iinita!
Niels Fabian Helge
von Koch (1870 - 1924)
1
Curva de Weierstrass
a curva de Weierstrass es, historicamente
hablando, el primer Iractal conocido. Fue
creado o descubierto (segun las preIerencias
IilosoIicas del lector) por el matematico
Karl Weierstrass en 11. o notable en este
caso, respecto a la curva de Koch, es que
disponemos de la ecuacion, como serie inIinita,
de la curva:

=
=
0
) cos( ) (
n
n n
x b a x W 6
Para que la Iuncion carezca de
tangente unica en cada uno de sus
puntos, es necesario que:
0 a 1, b sea un entero impar
y a b ~
Karl Theodor Wilhelm
Weierstrass (1815 - 1897)
2 / 1 6 +
1
Algunas Iunciones complejas no poseen derivada en ningun punto
Ejemplo
: : f = ) (
y i x
y i x
y i x
y i x
:
:
:
: : :
:
: f : : f
: f
: :
: :
:
A + A
A A
=
A + A
A + A
=
A
A
=
A
A +
=
A
A +
=
'
A A
A A
A
0 0
0 0
0
lim lim
lim lim
) ( ) (
lim ) (
Sigamos dos caminos distintos:
x
y
: : A +
:
x A
y A
1
2
1 2
1 lim
0
=
A:
1 lim
0
+ =
A:
El limite no es unico, por lo tanto no existe limite.
Como z es arbitrario, no existe derivada en ningun punto.
(Iuncion continua en todo el
plano complejo porque sus
componentes u y v lo son)
1
Ejemplo
2
, , ) ( : : f =

'
+

'

A
A
+ A + =
A
A + A +
=
A
A +
=
A
A +
=
'
A
A
A
A
:
:
: : :
:
: : : : : :
:
: : :
:
: f : : f
: f
:
:
:
:
0
0
2 2
0
0
lim
) )( (
lim
, , , ,
lim
) ( ) (
lim ) (
Sigamos de nuevo los dos
caminos distintos anteriores:
(Iuncion continua en todo el
plano complejo porque sus
componentes u y v lo son)
1
2
: : : :
:
= A = A
A 0
lim ;
Como el limite debe ser unico:
: : : :
:
+ = A = A
A 0
lim ;
0 = + = : : : : :
a derivada existe solo en z 0 y vale 0.
Este ejemplo muestra como una Iuncion
puede ser diIerenciable en un punto sin
serlo en ningun otro de su entorno.

btener los puntos del plano complejo donde la funcin

es diferenciable. Calcular su derivada.
) Re( ) ( : : : f =
) ) ) ) )
) . J ) )
) )
y i x
y x y x x y i x x x
y i x
x iy x x x y y i x x
:
: : : : : :
:
: f : : f
:
:
: :
A + A
A A + A + A + A + A
=
=
A + A
+ A + A + + A +
=
=
A
A + A +
=
A
A +
A
A
A A
2
lim
lim
Re Re
lim lim
2
0
0
0 0
) ) )
)
0 ) 0 (
0 Re
lim
Re
lim
0 0
lim
: 0 z Si
0 0 0
=
'

= A =
A
A A
=
A
A +
=
A A A
f
:
:
: :
:
f : f
: : :

) ) )
) ) )
0 ;
0 ;
0
2
2
lim lim lim
: 0
2 2
lim
2
lim lim
: 0
: 0 z Si
0 0 0
0
2
0 0
=
=
|
,
|
=
=
= +
= =
A
A
=
A
A +
A + = A
+ = + + A =
=
A
A + A + A
=
A
A +
+ A = A
=
A A A
A
A A
y
x
y
x x
x iy x
x x
y
y x i
:
: f : : f
y i :
iy x iy x x
x
x iy x x x
:
: f : : f
i x :
y y :
x
x :
z0
0 z puntos los en ble diIerencia es no I(z) =
1
a existencia de derivada en un punto implica la
continuidad de la Iuncion en ese punto.
Supongamos que existe f (:):
. J
) ( ) ( lim 0 0 ) ( '
) ( lim
) ( ) (
lim
) ( ) ( lim
0 0
0
0
0
0
0 0
0
: f : f : f
: :
: :
: f : f
: f : f
: :
: : : :
: :
= =
=

20
A First Course in Complex Analysis
atthias Beck, Gerald archesi, and Dennis Pixton
21
x
y
:
: : A +
x A
y A
1
1
. J
. J

A
A +
+
A
A +
=
'
A
A
x
y x v y x x v
i
x
y x u y x x u
: f
x
x
) , ( ) , (
lim
) , ( ) , (
lim ) (
0
0
x
v
i
x
u
/:
/f
N
N
+
N
N
=
Seguimos el camino : sea Ay0
cuaciones de Cauchy-#iemann
. J . J
y i x
y x v i y x u y y x x v i y y x x u
:
: f : : f
: f
:
:
A + A
+ A + A + + A + A +
=
A
A +
= '
A
A
) , ( ) , ( ) , ( ) , (
lim
) ( ) (
lim ) (
0
0
Si la derivada existe, el limite
es independiente del camino
22
x
y
:
: : A +
x A
y A
2
2
y
v
y
u
i
/:
/f
N
N
+
N
N
=
Seguimos el camino : sea Ax0
xy y x v y x y x u iy x : : f 2 ) , ( ; ) , ( ; ) ( ) (
2 2 2 2
= = + = =
: y i x y i x
x
v
i
x
u
/:
/f
2 ) ( 2 ) 2 ( 2 = + = + =
N
N
+
N
N
=
: y i x x y i
y
v
y
u
i
/:
/f
2 ) ( 2 2 ) 2 ( = + = + =
N
N
+
N
N
=
Efemplo.
. J
. J

A
A +
+
A
A +
=
'
A
A
y
y x v y y x v
y
y x u y y x u
i : f
y
y
) , ( ) , (
lim
) , ( ) , (
lim ) (
0
0
2
y
v
y
u
i
x
v
i
x
u
N
N
+
N
N
=
N
N
+
N
N
gualando ambas expresiones:
gualando las partes real e imaginaria obtenemos las
ecuaciones de Cauchy-#iemann:
Tenemos:
x
v
i
x
u
/:
/f
N
N
+
N
N
=
y
v
y
u
i
/:
/f
N
N
+
N
N
=
x
v
y
u
y
v
x
u
N
N
=
N
N
N
N
=
N
N
2
Despues de 20 aos de casi
'hibernacion compleja, entre
11 y 11 Cauchy y Riemman
Iundan el analisis complejo.
x
v
y
u
y
v
x
u
N
N
=
N
N
N
N
=
N
N
Augustin-Louis Cauchy
(1789-1857)
cuaciones de Cauchy-#iemman (C#)
Propuestas por primera vez por D`Alembert
en 12 en el contexto de la dinamica de
Iluidos.
2
Podemos dar en Iorma polar una Iuncion de variable
compleja cualquiera. Por ejemplo, sea:
) 0 (
1
) ( = + = :
:
: : f
En Iorma polar,
tendremos:

) , ( ) , (
sin
1
cos
1
) sin (cos
1
) sin (cos
) sin (cos
1
) sin (cos ) (
7 7
7 7
7 7 7 7
7 7
7 7
r v r u
r
r i
r
r
i
r
i r
i r
i r : f

'
+

'

'
+

'

+
= + +
=
+
+ + =
2
) ) , (
sin cos
i v(r,0 r u f(:)
0) i 0 r( :
+ =
+ =
7
En Iorma polar
tenemos:
) 0 (
1 1

N
N
=
N
N
N
N
=
N
N
r
u
r r
v v
r r
u
7 7
C# en forma polar
Demostrar que las ECR toman la Iorma:
Ejercicio: Comprobarlo para la Iuncion I(z) 1/z.
2
Recuerda que hemos tomado dos caminos muy particulares
para encontrar las ECR. Hemos demostrado que si
f(:) u(x,y)iv(x,y) es diIerenciable en un punto :
0
,
entonces las primeras derivadas parciales de u(x,y) y v(x,y)
existen en ese punto y satisIacen en el las ECR.
Ademas, podemos calcular el valor de f (:
0
) a traves
de las expresiones:
as ECR son una condicin necesaria para la derivabilidad.
x
v
i
x
u
/:
/f
N
N
+
N
N
=
y
v
y
u
i
/:
/f
N
N
+
N
N
=
2
) 2 ( ) (
) ( ) (
2 2
2
xy i y x
y i x : f
+ =
+ =
y
x
v
y
y
u
x
y
v
x
x
u
2 , 2
, 2 , 2
=
N
N
=
N
N
=
N
N
=
N
N
Efemplo8. 'eamos que , que hemos probado
que es diIerenciable en todas partes, cumple las ECR:
Sin embargo para:
2
) ( : : f =
) ( , , ) (
2 2 2
y x : : f + = =
0 , 2
, 0 , 2
=
N
N
=
N
N
=
N
N
=
N
N
x
v
y
y
u
y
v
x
x
u
as ECR no se satisIacen excepto
para z 0. Entonces la derivada no
existe para ningun z distinto de 0.
Pero no podemos asegurar la
existencia de la derivada en z 0,
aunque en este caso la hemos
demostrado anteriormente.
2 ) 0 , 0 (
) 0 , 0 (
) 0 , 0 (
) 0 , 0 (
0
1
x
v
y
u
y
v
x
u
N
N
= =
N
N

N
N
= =
N
N
'eamo8 un efemplo, un tanto artificial, /on/e veamo8 que la8 ECR 8on
nece8aria8 pero no 8uficiente8

,
|
=
=
=
0 , 0
0 ,
) (

:
:
:
:
: f

0
0 0
lim ) 0 ( '
) (
lim
0
) 0 ( ) (
lim ) 0 ( '

'
+

'

=
=

:
:
f
:
: f
:
f : f
f
:
: :
"ue tiene valor 1 sobre el eje real y -1 sobre la
linea y x, p.ej. De modo que I(z) no tiene
derivada en z 0.
Y sin embargo, las condiciones
de CR en z 0 se cumplen:
De modo que las condiciones
son necesarias, pero no
suficientes.
Calculemos su derivada en z 0:
0
Condiciones suficientes de derivabilidad
Sea f(:) u(x,y) iv(x,y) deIinida en un entorno del punto
:
0
x
0
iy
0
, supongamos que las primeras derivadas parciales de
u(x,y) y v(x,y) existen en el entorno de ese punto y son continuas
en z

. Entonces, si las parciales satisIacen las ECR en :

0
, la derivada
f (:) en :
0
existe.
. 0 0 cuando 0 0 donde
)} , ( ) , ( )} , ( ) , (
) , ( ) , (
1 1
1 1
1 1
A A
A + A + A
N
N
+ A
N
N
= A
= A

'
+

'

+
N
N
+ A

'
+

'

+
N
N
= A
= A + + A + A + A + = A
= A + A + = A
y y x y
y x y
y
u
x
x
u
u
y
y
u
x
x
u
u
y x u y y x u y y x u y y x x u u
y x u y y x x u u
s
s
s
Sumamos y restamos
1
. 0 0 cuando 0 0 donde
2 2
2 2
A A
A + A + A
N
N
+ A
N
N
= A
y y x y
y x y
y
v
x
x
v
v
s
s
De la misma manera, para v(x,y):
. 0 0 cuando
0 0 donde
2 1 2 1
A A
+ = + =
A + A + A

'
+

'

N
N
+
N
N
+ A

'
+

'

N
N
+
N
N
= A + A = A
y y x
i y i
y x y
y
v
i
y
u
x
x
v
i
x
u
v i u
s s s
s
Asi que:
Podemos utilizar en esta ultima igualdad las ECR:
x
v
y
u
y
v
x
u
N
N
=
N
N
N
N
=
N
N
2
x
v
i
x
u
:

/:
/
: f
y x y i x
x
v
i
x
u

y x y
x
u
i
x
v
x
x
v
i
x
u
v i u
:
:
y i
x
v
i
x
u
N
N
+
N
N
=
A
A
= =
A + A + A + A

'
+

'

N
N
+
N
N
= A
A + A + A

'
+

'

N
N
+
N
N
+ A

'
+

'

N
N
+
N
N
= A + A = A
A
A
A

'
+

'

N
N
+
N
N
0
lim ) ( '
) ( s
s


y x y
y
v
i
y
u
x
x
v
i
x
u
v i u A + A + A

'
+

'

N
N
+
N
N
+ A

'
+

'

N
N
+
N
N
= A + A = A s
x
v
y
u
y
v
x
u
N
N
=
N
N
N
N
=
N
N

studiar la derivabilidad de la funcin

y en caso afirmativo hallar la derivada.
2 1
) ( :
:
: f + =
)
2 2 2 2
2
2 2
) (
y x
y
i
y x
y x x
: f
+

+
+ +
=
u
iv
)
) 0 2
0 2
2
2 2
2
2 2
= +
N
N
=
N
N
= +
N
N
=
N
N
y x y
x
v
y
u
y x x
y
v
x
u
se cumplen las ECR
solo en x0, y0
C Z
= =
z derivable no I(z)
0 y 0, x para deIinidas estan no y) y v(x, y) u(x, Pero
xamen
1UNI 02/03: P-1

Funciones analticas u holomorfas

&na Iuncion f(:) es analtica (u holomorfa) en un
abierto A si posee derivada en todo punto de A.
Cuando se dice que una Iuncion f es
analitica en un conjunto S que no es
abierto, quedara sobrentendido que f es
analitica en algun abierto que contiene a S.
Cuando decimos que una Iuncion
es analitica en un punto :
0
, la
derivada debe existir en todos los puntos
de algun entorno de z
0
.
ota: observa que f(:) ,:,
2
es solo derivable en
: 0, pero tampoco ahi es analitica.
x
y
0
:
x
y
A

) , ( ) , ( ) ( y x v i y x u : f + =
continua en un dominio D:
Existe una Iorma rapida y Iacil de comprobar
si una Iuncion f (:) es analitica?
Sea
x
v
y
u
y
v
x
u
N
N
=
N
N
N
N
=
N
N
en todo punto de D.
f(:) es analitica en un dominio D 8ii u(x,y) y v(x,y)
son continuas y poseen primeras derivadas parciales
continuas en D y satisIacen las ecuaciones de C#:

#esumen: Es f(z) analtica en z

0
?
1. Escribe f(z) como f(z) = u(x,y) + iv(x,y).
2. Encuentra u
x
(x,y), u
y
(x,y), v
x
(x,y) y v
y
(x,y).
3. Comprueba que se cumplen las ecuaciones
de Cauchy-#iemann:
u
x
(x
0
,y
0
) = v
y
(x
0
,y
0
)
u
y
(x
0
,y
0
) = -v
x
(x
0
,y
0
)
4. Comprueba que u
x
(x,y), u
y
(x,y),v
x
(x,y) y
v
y
(x,y) son continuas en (x
0
,y
0
).

'
+

'

'
+

'

+
=

+
=
2 2 2 2
1
) (
y x
y
i
y x
x
y i x
y i x
y i x
: f
2 2 2 2 2 2
2 2
) (
2
,
) ( y x
xy
x
v
y
u
y x
y x
y
v
x
u
+

=
N
N
=
N
N
+
+
=
N
N
=
N
N
Ejemplo
Es 1/: analitica?
as ecuaciones de Cauchy-Riemann se cumplen. Pero I(z)
no es continua en cero ni sus parciales tampoco.
a Iuncion es analitica en todo punto, excepto en z 0.
) , ( y x u
) , ( y x v
0

+
+

+

=
+
+
-

+ +
=

+ +
=

+
=
2 2 2 2
2 2
) 1 (
2
) 1 (
1
) 1 (
) 1 (
) 1 (
) 1 (
1
1
1
1
) (
y x
y
i
y x
y x
y i x
y i x
y i x
y i x
y i x
y i x
:
:
: f
u
v
. J
. J . J
x
v
y x
x y
y
u
y
v
y x
y x
x
u
N
N
=
+

=
N
N
N
N
=
+

=
N
N
2
2 2
2
2 2
2 2
) 1 (
) 1 (
,
) 1 (
) 1 ( 2
excepto en x 1 e y 0, en : 1.
Ejemplo
Es (1z)/(1-z) analitica?
Al igual que antes, la Iuncion es analitica en todo punto,
1
2

ota: Para resolver este problema se usa notacion exponencial

que no veremos hasta el capitulo siguiente. Puedes volver a el
mas adelante.

45
#espuesta.
Encontrar todas las posibles funciones complejas
f(z) = u(x,y) + iv(x,y) analticas en la regin D = {z c C/ |z| > 3}, que
cumplan simultneamente:
(a) #e(f(z)) = u(x)
(b) f(0) = 0
(c) mx |f(z)| = 6, z c D
1. f(z) = u(x) + iv(x,y) analtica en D => Se cumplen ecuaciones de
Cauchy #iemann en D

,
|
= = = Z = =
= = = =

/y
/v
/x
/u
: f D y x
/y
/v
/x
/u
v v
v(y) v u(x) u v u
y x
x y
) ( ) , ( ,
ser por , 0
46
R C B
C y v
B x u
Z
|
,
|
+ =
+ =
, ,
2. f(0) = 0 = B + iC B = 0, C = 0
: iy x : f
y v
x u
= + =
|
,
|
)
`

=
=
) ( ) (
3.
|
,
|
=
=
= = = =
=
Z Z Z
: : f
: : f
: : : f
D : D : D :
2 ) (
2 ) (
: Iunciones Dos
2 max max ) ( max
2
1

47
P2. Junio 2006
a) De la funcin f(z) se sabe:
1. Es analtica en |z 2| < 3,
2. f(z) = f(z) en |z 2| < 3,
3. |f(z)| =
#espuesta.
Dar la expresin de f(z) en |z 2| < 3 y, en particular, calcular el
valor de f(2 + i).

f(z) = u(x,y) + iv(x,y)

D : |z - 2| < 3
48
1.- f(z) analtica en D.
D. en

,
|
=
=

x y
y x
v u
v u
Riemann Cauchy
2.- f(z) = f(z), en D.
D. en , 0 ) , (
D. en ), , ( ) , ( ) , ( ) , (
=
= +
y x v
y x iv y x u y x iv y x u
49
De las condiciones 1 y 2,
D. en . ) ( D en D. en
0
0
cte : f cte u
u
u
y
x
= =
|
,
|
=
=
3.- |f(z)| =

f(z) = en D.
z = 2+i pertenece a D:
f(2 + i) =

0
Sol.: (a) a -b; c 1. (b) a b -1
(a) En ningun punto. (b) En ningun punto.
(c) C - z i, -i} (d) C (e) En ningun punto.
(I) C - z 0} (g) En ningun punto.
1
2

(1) as Iunciones polinomicas son analiticas en todo punto.

Son Iunciones enteras.
n
n
: c : c : c : c : c c : f + + + + + + =

2
2 1 0
) (
Gracias a las propiedades de las derivadas, si dos Iunciones
son analiticas en un dominio D, su suma y su producto son
analiticos en D. Y su cociente es analitico en D si el
denominador no se anula en ningun punto de D.
&na composicion de Iunciones analiticas sera analitica.
) (
) (
) (
: h
: g
: f =
(2) a Iunciones racionales
donde g(z) y h(z) son polinomios,
son analiticas excepto, quizas,
en los puntos donde h(z) se anula.

ota: Derivada en el infinito

"ue tienen de especial las Iunciones analiticas?

'eremos mas adelante cosas como:
Si una Iuncion es analitica entonces todas sus derivadas tambien
son analticas (en Iranco contraste con las Iunciones de variable
real).
Toda Iuncion analitica puede expresarse como serie de potencias.
as Iunciones analiticas estan determinadas por sus ~valores de
contorno: si disponemos de los valores de una Iuncion analitica
para los puntos de la circunIerencia unidad, estos valores determinan
totalmente los valores en todo el circulo unidad. Podemos expresar
los valores de la Iuncion en los puntos interiores a traves de una
Iormula integral que involucra los valores del contorno.
0
Efercicio: Encontrar la Iorma mas general de la Iuncion
analitica f(:) cuya parte real u(x,y) es: u(x,y) x
2
- y
2
- x
Exigimo8 que 8e cumplan la8 ECR.
y
v
x
x
u
N
N
= =
N
N
1 2
(x) y xy x /y x x /y
y
v
y x v + = + = +
N
N
=

2 ) ( ) 1 2 ( ) ( ) , (
cte x
/x
x /
y
x
v
y
y
u
= = + =
N
N
= =
N
N
) (
) (
2 2
i : : : f
y xy i x y x y x iv y x u : f
+ =
+ + = + =
2
2 2
) (
) 2 ( ) , ( ) , ( ) (
ntegrando respecto a y:
Exigiendo que se cumpla la segunda ECR:
1
2
. Demostrar que si f(:) es analitica en un dominio D y
1(z) es constante en D, entonces f(:) es constante en D.
2 2 2
) , ( ) , ( , ) ( , y x v y x u : f = + =
Derivando con respecto a x e y:
0 2 2 ) ( 0 2 2 ) ( =
N
N
+
N
N
=
N
N
+
N
N
y
v
v
y
u
u b
x
v
v
x
u
u a
ultiplicando (a) por u y (b) por v:
0 ) ( 0 ) (
2 2
=
N
N
+
N
N
=
N
N
+
N
N
y
v
v
y
u
uv b
x
v
uv
x
u
u a

Exigiendo ECR y sumando ambas ecuaciones:

0 ) (
2 2
=
N
N
+
x
u
v u
y
v
x
u
N
N
=
N
N
x
v
y
u
N
N
=
N
N
ultiplicando (b) por u
y restando (a) por v, tenemos:
0 ) (
2 2
=
N
N
+
x
v
v u
Si
2
u
2
v
2
0 entonces u v 0 f(:) 0 (cte)
Si = 0 entonces u
x
u
y
v
x
v
y
0
u cte, v con8t f(:) cte
0 ) ( 0 ) (
2 2
=
N
N
+
N
N
=
N
N
+
N
N
y
v
v
y
u
uv b
x
v
uv
x
u
u a

Efercicio8:
(1) Demostrar el teorema de la derivada nula,
que si f (:) 0 en todos los puntos de un dominio D,
entonces f(:) es constante en D (Lo tiene8 re8uelto en el
8iguiente par /e tran8parencia8)
(2) Demuestra bajo las mismas condiciones, lo mismo
para Re(f), Im(f) o rg(f) constante en D.

Puntos singulares
&na singularidad o punto singular /e f (:) es un punto :
o
en el cual f (:) no es analitica, pero es analitica en algun
punto de todo entorno de z
0
. (Po8ee f(:) ,:,
2
8ingulari/a/e8)
Tipos de singularidades:
(1) Aislada: si existe un entorno para el que el unico punto singular
es z
0
. Si no podemos encontrar semejante entorno, la singularidad
es no aislada. Si I(z) tiene un numero Iinito de singularidades,
todas seran aisladas.
(2) vitable en z
0
: si el limite cuando z tiende a z
0
de I(z) es Iinito.
() sencial: es una singularidad que no es un polo (otro tipo de
singularidad que deIinimos a continuacion) ni es evitable.
() n el infinito: si g(z) I(1/z) tiene una singularidad en z 0,
decimos que I(z) tiene el mismo tipo de singularidad en el
inIinito.
0
Polos
(otro tipo de
singularidad)
&n polo de orden 3 de 1 (z) es un punto :
0
para el cual se cumple:
= ) ( ) ( lim
0
0
: f : :
n
: :

2
2
) (
2

+
=
:
:
: f
P.ej. El punto : 2 es un polo simple o de orden 1 de
porque
=
= 0 2 lim
) ( ) 2 ( lim
2
2
1
2
= +
=

:
: f :
:
:
El limite
existe y es diIerente de 0.
1
Observa que el orden de un polo es la 'potencia
del termino
o
: :
o
:
) )( (
2
12
2
) (
2
+

=
: :
:
: :
:
: f
:
o
-, son polos
simples.

) (
) (
i :
:
: f
+
=
:
o
-i es un polo de tercer orden.
2 2
) (
) (
+
=
:
:
: f
. J
2 2 2
) 2 ( ) 2 (
) 2 )( 2 (
) (
i : i :
:
i : i :
:
: f
+
=
+
=
Esta Iuncion tiene 2 puntos singulares, polos de 2 orden
en : -2i y : 2i
2
'isualizing complex analytic functions using domain coloring
Hans Lundmark, Department of Mathematics
(Linkping University, Sweden) http://www.mai.liu.se/~halun/complex/complex.html
2
) ( : : f =
1 ) ( = i f
i
i
1
1 ) ( = i f
i
ejor tener un patron
unico en el plano w y
observar que patron en
el plano z nos llevaria a el.

Gradiente de color
para el argumento
en el plano
Escala de grises
para modulo en
plano
Combinacion en
el plano .
Patron de reIerencia
en el plano , al que
hemos aadido una
parrilla cuadriculada.

) , ( ) , (
) (
7 7 r r
: : f

=
) 2 , ( ) , (
) (
2
2
7 7 r r
: : f

=
) , ( ) , (
) (

7 7 r r
: : f

=
) , ( ) , (
) (

7 7 r r
: : f

=
i 2 2 I I Esquinas
Estos son los patrones
en el plano z cuya
imagen bajo las
transIormaciones f(:)
acaban todas en el patron
de reIerencia.
Observa que un cero de
orden k en z
0
se
reconoce porque los anillos
sombreados se acumulan
en el y si recorremos un
pequeo circulo a su
alrededor en sentido
antihorario cambiaremos
ciclicamente de color
(de amarillo a negro)
k veces.

) )( 2 1 ( ) 2 ( ) (
2
i : i : : : f + + =
i :
:
i :
=
=
+ =
2
2 1
Plano z. Esquinas:
i I I
(raiz doble)
'eamos el polinomio:
Ceros del polinomio:

Aqui hacemos la parrilla mas

apreciable. Recuerda que la
imagen de esta cuadricula
distorsionada proporciona en
el plano una parrilla con
cuadrados de lado 1. Observa
que la transIormacion es
conIorme: los angulos se
preservan en la
transIormacion, si dos curvas
se intersectan con un angulo
determinado en el punto z
0
,
entonces sus imagenes bajo la
transIormacion I se intersectan
con el mismo angulo en I(z
0
).
Aqui estamos viendo el
Ienomeno en la direccion
inversa.
Plano z. Esquinas:
i I I
a conIormalidad se rompe en los puntos donde
la derivada de I se hace 0, en los llamados puntos
criticos de I. Puedes encontrar esos puntos en la Iigura?

ota sobre transIormaciones conIormes:

0
Teorema de Lucas
Si I es un polinomio,
entonces los ceros de
su derivada I` caen todos
en el poligono convexo
que tiene como aristas
a los ceros de I.
En el ejemplo que nos
ocupa, el poligono
convexo es el triangulo
de la imagen.
1
Como se ven los polos de una Iuncion racional bajo
este esquema de color?
os ciclos de color van en direccion opuesta (Si recorremos en
sentido horario van de negro a amarillo) y el valor absoluto crece
hasta inIinito a medida que nos aproximamos al polo (en lugar de
de desvanecerse como ocurre al acercarnos a un cero).
:
: f
1
) ( =
2
1
) (
:
: f =
Polo simple en z 0.
Polo de segundo orden en z 0.
2
'eamos una transIormacion de oebius o bilineal:
1
1
) (
+

=
:
:
: f
&n cero en z 1 y un polo simple en z -1.
Plano z. Esquinas:
i 2 2 I I

Funciones armnicas
u(x,y) y v(x,y), las componentes de una Iuncion analitica,
son funcione8 armonica8. cumplen la 0. d0 Lapla.0
Partiendo de
la ECR:
x
v
y
u
y
v
x
u
N
N
=
N
N
N
N
=
N
N
y
y x
v
y
u
y x
v
x
u
N N
N
=
N
N
N N
N
=
N
N
2
2
2 2
2
2
y
0
2
2
2
2
=
N
N
+
N
N
y
u
x
u
Derivando
respecto
a x e y:
0
2
2
2
2
=
N
N
+
N
N
y
v
x
v
Derivando
respecto a
y y x:
Suponiendo que sus segundas derivadas existen y son continuas
(mas adelante se demostrara que si I es analitica en :
0
, u y v poseen
parciales continuas de todo orden en ese punto):

&na Iuncion (x,y) es armnica en un dominio si (x,y)

es C
2
(i.e.: tiene derivadas parciales hasta el orden 2 y son
continuas) y satisIace la ecuacin de Laplace en dicho
dominio:
0
2
2
2
2
2
=
N
N
+
N
N
= ]
y x
Hemos visto que si f(:) es analitica en cierto dominio, entonces su
parte real u(x,y) y su parte imaginaria v(x,y) son armonicas en dicho
dominio (ambas cumplen la ecuacion de aplace).
Dada una (x,y) armonica en un dominio simplemente conexo D,
existe una Iuncion analitica en D cuya parte real es (x,y) y tambien
existe una Iuncion analitica en D cuya parte imaginaria es (x,y).
Dada una Iuncion armonica u(x,y), parte real de una Iuncion compleja,
decimos que v(x,y) es la Iuncion armnica conjugada de u(x,y), si
u(x,y) iv(x,y) es analitica.

1 2 y 2 =
N
N
=
N
N
y
y
u
x
x
u
Efemplo. 'erificar que u(x,y) x
2
- y
2
- y e8 armonica en to/o
el plano complefo y encontrar la funcion armonica confuga/a
v(x,y)
0 2 y 2
2
2
2
2
2
2
2
2
=
N
N
+
N
N
=
N
N
=
N
N
y
u
x
u
y
u
x
u
Si v(x,y) es la armonica conjugada de u(x,y), entonces
ambas cumplen las ECR:
1 2 y 2 =
N
N
=
N
N
=
N
N
=
N
N
y
x
v
y
u
x
y
v
x
u

(x) xy x /y x x /y
y
v
y x v + = + = +
N
N
=

2 ) ( 2 ) ( ) , (
c x xy y x v
c x x
/x
x /
y
x
v
y
y
u
+ + =
+ = =
N
N
= =
N
N
2 ) , (
) (
) (
2 1 2
c) i (: : : f
c) x xy i ( y - y x i v u f(:)
+ + =
+ + + = + =
2
2 2
) (
2
x
y
v
x
u
2 =
N
N
=
N
N

(a) 'eriIica que u(x, y) x

xy
2
y es armonica en todo
el plano complejo.
(b) Encontrar la Iuncion armonica conjugada de la Iuncion u.
0
, , , ) (
2
2
2
2
2
2
2
2
2 2
= =
N
N
+
N
N
=
N
N
=
N
N
=
N
N
=
N
N
x x
y
u
x
u
x
y
u
xy
y
u
x
x
u
y x
x
u
a
C x y y x x,y v
C x x h x h x h xy
x
v
x h y y x y x, v
xy
y
u

x
v
y x
x
u
y
v
b
+ + =
+ = = + =
N
N
+ =
+ =
N
N
=
N
N
=
N
N
=
N
N
) ( : entonces Y
) ( , ) ( ' ), ( '
) ( ) ( primera, la ntegrando
; ) (
2
2
2 2
Como veremos en el siguiente capitulo..
0
En el siguiente ejercicio se resuelve la misma cuestion de
Iorma alternativa...
1
2

(a) v(x,y) -x k
(b) -e
x
cos y k
(c) v(x,y) |(y-1)
2
- (x1)
2
|/2 k
(d) v(x,y) cos x senh y k
(e) v(x,y) arg z k
(I) v(x,y)
xy e
y x
+

) 2 cos(
2 2

100
101
102
Efercicio. Demostrar que si u y v son armonicas conjugadas
mutuamente, entonces son Iunciones constantes.
Efercicio. Si u es armonica conjugada de v en un dominio D,
entonces u es armonica conjugada de v en D.
xy y x v y x y x u iy x : : f 2 ) , ( ; ) , ( ; ) ( ) (
2 2 2 2
= = + = =
v(x,y) es armonica conjugada de u(x,y), pero que si
intercambiamos ambas no es cierto. Es decir, que
2 2
) , ( ; 2 ) , ( ); , ( ) , ( ) ( y x y x v xy y x u y x iv y x u : f = = + =
no es analitica.
Efercicio. Demuestra que para
10
Nikolai gorovich Zhukovskii (1847-1921)
(o Zhukovsky o Joukowski)
a transIormacion de
Zhukovsky
:
:
1
+ =
as general:
:
a
:
2
+ =
a imagen de un circulo que pasa por z 1 o z -1 es una curva
similar a la seccion transversal de un ala de avion.
10

,
|
=
= =
+
2 2
2
) (
7
6
7
7
r r
r
: : f
Puntos de ramificacin y cortes de rama
Para univaluar la raiz cuadrada de z hagamos como en el caso real,
tomando arbitrariamente una de las dos posibilidades:
0
7
r : = =
) (: f
2
0
7
r =
Si giramos siguiendo un camino
continuo como muestra la Iigura
tendremos:
6 7 2
0
+
= r :
) (: f
6
7
+
=
2
0
r
I(z) suIre una crisis de identidad!
10
Este camino continuo
no nos genera problemas.
Cual es la diIerencia?
Rodear el origen z 0
parece ser lo que nos
genera la crisis.
z 0 es en este caso un
punto de ramificacin de
la Iuncion raiz cuadrada.
"ue ocurre si damos dos
vueltas alrededor del origen?
10
Decimos que z
0
es un punto de ramificacin de I(z) si
el valor de I(z) no regresa a su valor original cuando
trazamos una curva cerrada alrededor de el, de manera
que f vara de forma continua a medida que recorremos
la curva.
Observacion: debe ocurrir para cualquier curva alrededor
de z
0
(lejana o cercana). a Iuncion no tiene por que ser
continua o existir en z
0
.
10
Cual es la region mas grande posible sin crisis de identidad?
Para todos los puntos
de la region R la raiz cuadrada
esta univaluada.
Deseamos una region, lo mayor
posible, tal que no exista
posibilidad de trazar un camino
continuo y cerrado que contenga
al origen en su interior: una rama.
Region inIinitesimal alrededor
del eje x positivo.
10
&nivaluamos la Iuncion raiz cuadrada 'cortando
el plano complejo a lo largo del eje real positivo.
Rama
6 7 2 0 6 7 6
Rama
Cortes de rama
A es un punto inIinitesimalmente cercano
al corte por arriba. Y B por abajo. a Iuncion
es discontinua a traves del corte de rama.
ota: El corte es totalmente arbitrario.
10
Hojas y superficies de #iemann
En la superIicie de Riemann la Iuncion esta univaluada. Cada rama
corresponde a un piso (hoja de Riemman). Para el caso de la raiz
cuadrada: las vueltas impares 'tocan arriba y las pares 'abajo.
110
SuperIicie de Riemann para I(z) z
1/
I(z) z
1/n
tendra
n hojas de Riemann.
En particular si I(z)
no posee puntos
de ramiIicacion,
la superIicie de
Riemann coincide
con el plano
complejo C.