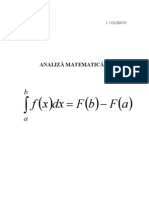Probleme de Analiza Matematica Si Ecuatii Diferentiale

GHEORGHE PROCOPIUC
PROBLEME
DE
ANALIZ
A MATEMATIC
A
SI
ECUATII DIFERENTIALE
IASI, 2007
Cuprins
1 Elemente de teoria spat iilor metrice 4
1.1 Spat ii metrice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2 Mult imea numerelor reale . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2 Siruri si serii 15
2.1 Siruri de numere reale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.2 Principiul contract iei . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.3 Siruri n R
p
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.4 Serii de numere reale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.5 Serii cu termeni pozitivi . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.6 Serii cu termeni oarecare . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
3 Limite de funct ii 42
3.1 Limita unei funct ii reale de o variabila reala . . . . . . . . . . . . . . . . . 42
3.2 Limita unei funct ii de o variabila vectoriala . . . . . . . . . . . . . . . . . 45
4 Funct ii continue 49
4.1 Continuitatea funct iilor reale de o variabila reala . . . . . . . . . . . . . . 49
4.2 Continuitatea uniforma a funct iilor de o variabila . . . . . . . . . . . . . . 51
4.3 Continuitatea funct iilor de o variabila vectoriala . . . . . . . . . . . . . . 53
5 Derivate si diferent iale 55
5.1 Derivata si diferent iala funct iilor de o variabila . . . . . . . . . . . . . . . 55
5.2 Proprietat i ale funct iilor derivabile . . . . . . . . . . . . . . . . . . . . . . 59
5.3 Derivatele si diferent iala funct iilor de n variabile . . . . . . . . . . . . . . 64
6 Funct ii denite implicit 74
6.1 Funct ii denite implicit de o ecuat ie . . . . . . . . . . . . . . . . . . . . . 74
6.2 Funct ii denite implicit de un sistem de ecuat ii . . . . . . . . . . . . . . . 77
6.3 Transformari punctuale . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
6.4 Dependent a si independent a funct ionala . . . . . . . . . . . . . . . . . . . 81
6.5 Schimbari de variabile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
2
CUPRINS 3
7 Extreme pentru funct ii de mai multe variabile 87
7.1 Puncte de extrem pentru funct ii de mai multe variabile . . . . . . . . . . 87
7.2 Extreme pentru funct ii denite implicit . . . . . . . . . . . . . . . . . . . 89
7.3 Extreme condit ionate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
8 Siruri si serii de funct ii 93
8.1 Siruri de funct ii reale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
8.2 Serii de funct ii . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
8.3 Serii de puteri . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
8.4 Serii Taylor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
9 Elemente de geometrie diferent iala 104
9.1 Curbe plane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
9.2 Curbe n spat iu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
9.3 Suprafet e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
10 Integrala Riemann si extinderi 122
10.1 Primitive. Integrala nedenita . . . . . . . . . . . . . . . . . . . . . . . . . 122
10.2 Integrala denita . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
10.3 Integrale improprii . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
10.4 Integrale cu parametri . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
11 Integrale curbilinii 140
11.1 Lungimea unui arc de curba . . . . . . . . . . . . . . . . . . . . . . . . . . 140
11.2 Integrale curbilinii de primul tip . . . . . . . . . . . . . . . . . . . . . . . 141
11.3 Integrale curbilinii de tipul al doilea . . . . . . . . . . . . . . . . . . . . . 143
11.4 Independent a de drum a integralelor curbilinii . . . . . . . . . . . . . . . . 146
11.5 Calculul ariei cu ajutorul integralei curbilinii . . . . . . . . . . . . . . . . 147
12 Integrale multiple 148
12.1 Integrala dubla . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
12.2 Aria suprafet elor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
12.3 Integrala de suprafat a de primul tip . . . . . . . . . . . . . . . . . . . . . 157
12.4 Integrale de suprafat a de tipul al doilea . . . . . . . . . . . . . . . . . . . 158
12.5 Integrala tripla . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160
13 Ecuat ii diferent iale ordinare 167
13.1 Ecuat ii diferent iale de ordinul ntai . . . . . . . . . . . . . . . . . . . . . . 167
13.2 Alte ecuat ii integrabile prin metode elementare . . . . . . . . . . . . . . . 173
13.3 Ecuat ii diferent iale de ordin superior . . . . . . . . . . . . . . . . . . . . . 175
13.4 Ecuat ii carora li se poate micsora ordinul . . . . . . . . . . . . . . . . . . 176
14 Ecuat ii si sisteme diferent iale liniare 178
14.1 Sisteme diferent iale liniare de ordinul ntai . . . . . . . . . . . . . . . . . . 178
14.2 Sisteme diferent iale liniare cu coecient i constant i . . . . . . . . . . . . . 180
14.3 Ecuat ii diferent iale liniare de ordinul n . . . . . . . . . . . . . . . . . . . . 184
14.4 Ecuat ii de ordinul n cu coecient i constant i . . . . . . . . . . . . . . . . . 187
CUPRINS 4
14.5 Ecuat ia lui Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
Capitolul 1
Elemente de teoria spat iilor
metrice
1.1 Spat ii metrice
1.1 Fie (G, +) un grup comutativ si p : G R
+
o funct ie ce satisface proprietat ile:
1) p(x) = 0 d.d. x = 0;
2) p(x) = p(x), x G;
3) p(x +y) p(x) +p(y), x, y G.
Sa se arate ca aplicat ia d : GG R, d(x, y) = p(x y), x, y G este o metrica
pe G.
R: Vericam ca d satisface axiomele metricii: 1
o
. d(x, y) = p(x y) 0, x, y G
pentru ca x y = x + (y) G si d(x, y) = 0 p(x y) = 0 x y = 0 x = y;
2
o
. d(x, y) = p(x y) = p(x + y) = p(y x) = d(y, x); 3
o
. d(x, y) = p(x y) =
p(x z +z y) p(x z) +p(z y) = d(x, z) +d(z, y), x, y, z G.
1.2 Fie N mult imea numerelor naturale. Sa se arate ca urmatoarele aplicat ii sunt
distant e pe N:
1) d : NN R
+
, d(m, n) = [mn[, m, n N.
2) d : N
R
+
, d(m, n) =
1
m

1
n
, m, n N
.
3) d : NN R
+
, d(m, n) =
m
1+m

n
1+n
, m, n N.
1.3 Fie R
n
= R R R, produsul cartezian constand din n 1 factori si
x = (x
1
, x
2
, . . . , x
n
), y = (y
1
, y
2
, . . . , y
n
) R
n
. Sa se arate ca aplicat iile: d, , :
R
n
R
n
R
+
, denite prin:
d(x, y) =
_
n
k=1
(x
k
y
k
)
2
, (x, y) =
n
k=1
[x
k
y
k
[, (x, y) = max
k=1,n
[x
k
y
k
[
sunt metrici pe R
n
.
5
CAPITOLUL 1. ELEMENTE DE TEORIA SPAT IILOR METRICE 6
R: Pentru d se aplica inegalitatea lui Minkowski:
_
n
k=1
(a
k
+b
k
)
2
_
n
k=1
a
2
k
+
_
n
k=1
b
2
k
, a = (a
1
, a
2
, . . . , a
n
), b = (b
1
, b
2
, . . . , b
n
).
1.4 Sa se hasureze n R
2
sferele deschise S(0, r), r > 0, relative la metricile d, , .
1.5 Sa se arate ca d, , sunt metrici echivalente pe R
n
.
R: Se demonstreaza inegalitat ile:
n d n n n
n .
1.6 Sa se arate ca d : RR R
+
, d(x, y) =
|xy|
1+|xy|
, x, y R este o metrica pe R.
R: Se t ine seama ca oricare ar a, b, c 0 cu a b +c, avem:
a
1 +a
a
b
1 +b
b +
c
1 +c
c,
deoarece din 0 urmeaza

1+

1+
.
1.7 Fie d : XXR
+
o metrica pe X. Sa se arate ca aplicat ia : XXR
+
denita prin (x, y) =
d(x,y)
1+d(x,y)
este de asemenea o metrica pe X.
1.8 Sa se arate ca ntr-un spat iu metric (X, d) avem:
1) d(x
1
, x
n
)
n
i=1
d(x
i
, x
i+1
), x
1
, . . . , x
n
X, n 2.
2) [d(x, z) d(z, y)[ d(x, y), x, y, z X.
3) [d(x, y) d(x
, y
)[ d(x, x
) +d(y, y
), x, x
, y, y
X.
R: 3) d(x, y) d(x, x
) +d(x
, y) d(x, x
) +d(x
, y
) +d(y
, y).
1.9 Fie X o mult ime nevida. Sa se arate ca aplicat ia d : X X R, denita prin:
d(x, y) =
_
0, x = y
1, x ,= y
este o metrica pe X (metrica discreta pe X).
1.10 Sa se arate ca aplicat ia d : R
+
R
+
R
+
, denita prin:
d(x, y) =
_
x +y, x ,= y,
0, x ,= y
este o metrica pe R
+
.
1.11 Sa se arate ca aplicat ia d : R
n
R
n
R, denita prin:
d(x, y) =
n
k=1
1
2
k

[x
k
y
k
[
1 +[x
k
y
k
[
,
x = (x
1
, x
2
, . . . , x
n
), y = (y
1
, y
2
, . . . , y
n
) R
n
este o metrica pe R
n
.
1.12 Sa se arate ca urmatoarele aplicat ii sunt metrici pe mult imile indicate:
1) d : (0, ) (0, ) R, d(x, y) =
1
x

1
y
.
2) d : RR R, d(x, y) =
x
1+
1+x
2
x
y
1+
1+y
2
.
3) d : R
2
R
2
R,
d(x, y) =
_
[x
2
y
2
[, x
1
= y
1
,
[x
2
[ +[y
2
[ +[x
1
y
1
[, x
1
,= y
1
,
(metrica mersului prin jungla), unde: x = (x
1
, y
1
), y = (y
1
, y
2
).
4) d : R
2
R
2
R,
d(x, y) =
_ _
(x
1
x
2
)
2
+ (x
2
y
2
)
2
, daca exista o dreapta R
2
a.. 0, x, y ,
_
x
2
1
+x
2
2
+
_
y
2
1
+y
2
2
, n rest,
(metrica caii ferate franceze), unde: 0 = (0, 0), x = (x
1
, y
1
), y = (y
1
, y
2
).
1.13 Sa se arate ca urmatoarele aplicat ii sunt norme pe R
n
:
1) [[x[[ =
k=1
x
2
k
, x = (x
1
, x
2
, . . . , x
n
) R
n
.
2) [[x[[ =
n
k=1
[x
k
[, x = (x
1
, x
2
, . . . , x
n
) R
n
.
3) [[x[[ = sup [x
k
[, k = 1, n, x = (x
1
, x
2
, . . . , x
n
) R
n
.
1.14 Fie / = A =
_
a +bi c +di
c +di a bi
_
, cu a, b, c R, i
2
= 1 si f : / R
+
,
f(A) =

det A. Sa se arate ca (/, [[ [[) este spat iu normat n raport cu norma data
prin [[A[[ = f(A).
1.15 Fie (
0
[1,e]
= f : [1, e] R, f continua pe [1, e]. Sa se arate ca aplicat ia [[ [[ :
(
0
[1,e]
R denita prin [[f[[ =
__
e
1
(f
2
(x) ln x) dx
1/2
este o norma pe (
0
[1,e]
si sa se
gaseasca norma funct iei f(x) =
x.
1.16 Fie (
1
[0,1]
= f : [0, 1] R, f derivabila cu derivata continua pe [0, 1]. Sa se
arate ca urmatoarele aplicat ii sunt norme pe (
1
[0,1]
:
1) [[f[[ = sup [f(x)[, x [0, 1] . 2) [[f[[ =
_
1
0
[f(x)[ dx.
3) [[f[[ = [f(0)[ + sup [f(x)[, x [0, 1] . 4) [[f[[ =
_
_
1
0
f
2
(x) dx
_
1/2
.
1.17 Fie mult imea X = 1, 2, 3, 4 si clasele:
1
= , X, 2, 1, 2, 2, 3, 1, 2, 3,
2
= , X, 1, 2, 3, 4, 2, 3, 4.
1) Sa se arate ca
1
este topologie pe X dar
2
nu este topologie pe X.
2) Sa se gaseasc a sistemele de vecinatat i ale punctelor 3 si 4 din spat iul topologic
(X,
1
).
R: Se verica proprietat ile din denit ia topologiei. Pentru
2
se constata ca, de
exemplu 1 2 = 1, 2 /
2
.
1.18 Fie X = , , , si familia de mult imi:
= , , , , , , , , , , X.
Sa se arate ca este o topologie pe X si sa se determine sistemele de vecinatat i ale
punctelor , , si .
1.19 Daca X ,= si
0
= , X, atunci (X,
0
) este spat iu topologic pe X, numit
spat iul topologic nondiscret (grosier) pe X.
1.20 Daca X ,= si T(X) este mult imea tuturor part ilor mult imii X, iar
1
= T(X),
atunci (X,
1
) este spat iu topologic pe X, numit spat iul topologic discret pe X.
1.21 Daca X are mai mult de doua elemente si a X, xat, atunci = , a, X
este o topologie pe X, diferita de topologia nondiscreta si de cea discreta.
1.22 Fie X = a, b, c, d, e. Sa se precizeze care dintre urmatoarele familii de part i ale
lui X este o topologie pe X:
1)
1
= , X, a, a, b, a, c.
2)
2
= , X, a, b, c, a, b, d, a, b, c, d.
3)
3
= , X, a, a, b, a, c, d, a, b, c, d.
R:
1
si
2
nu,
3
da.
1.23 Fie = , R, (q, ), q Q. Sa se arate ca este o topologie pe R.
R: Mult imea A =

qQ
(q, ), q >
2 = (
2, ) este o reuniune de mult imi din ,

totusi ea nu apart ine lui deoarece

2 / Q.
1.24 Pe mult imea X = a, b, c urmatoarele familii de part i ale lui X sunt topologii:
1
= , X, a, b, c;
2
= , X, a, a, c;
3
= , X, b, a, c;
4
= , X, c, b, c.
1.25 Fie = , R, (, ), > 0. Sa se arate ca este o topologie pe R.
1.26 Pe mult imea X = 1, 2, 3, 4, 5 se considera topologia:
= , X, 1, 1, 2, 1, 3, 4, 1, 2, 3, 4, 1, 2, 5.
1) Sa se gaseasca punctele interioare ale mult imii A = 1, 2, 3.
2) Sa se gaseasca punctele exterioare ale mult imii A.
3) Sa se gaseasca punctele frontiera ale mult imii A.
R: 1) Int A = 1, 2 deoarece 1 1, 2 A, 2 1, 2 A. 3 nu este punct interior
lui A deoarece nu apart ine la nici o mult ime deschisa inclusa n A. 2) (A = 4, 5 si
Int (A = , deci nu exista puncte exterioare lui A. 3) Fr A = 3, 4, 5.
1.27 Sa se arate ca urmatoarele familii de part i sunt topologii pe R:
1)
i
= , R, (a, ), a R, (topologia inferioara sau dreapta a lui R).
2)
s
= , R, (, a), a R, (topologia superioara sau stanga a lui R).
1.28 Sa se gaseasca interiorul, exteriorul si frontiera intervalului I = [3, ) relativ la
spat iul topologic (R,
i
), unde
i
este topologia inferioara pe R.
R: Cea mai ampla mult ime deschisa, cont inuta n I, este (3, ), deci Int A = (3, ).
(I = (, 3) si nu cont ine nici o alta mult ime deschisa n afara de mult imea vida.
Int (A = , Fr A = (, 3].
1.2 Mult imea numerelor reale
1.29 Sa se arate ca mult imea A = x
n
=
n
n +
1
n
n
+
1
n
+ 1, n N, n 2 este
marginita.
R: Din x +
1
x
2 pentru orice numar real pozitiv, rezulta x
n
> 2 + 0 + 1 = 3, adica
a = 3 este un minorant pentru A. Cum pentru n 2, 1 <
n
n < 2 si
1
n

1
2
, urmeaza
x
n
< 2 + 1 +
1
2
+ 1 =
9
2
, adica b =
9
2
este un majorant pentru A.
1.30 Sa se arate ca mult imea A
= y R, y =
x+1
x
2
+x+2
, x R este marginit a pentru
orice R si sa se determine inf A
si sup A
.
R: Fie y A
. Atunci: yx
2
+ (y )x + 2y 1 = 0, care trebuie sa aiba solut ii
reale. Deci (y )
2
4y(2y 1) = 7y
2
2( 2)y +
2
0, de unde, notand cu
= 2
2
2
+ 1,:
y
_
2
7
,
2 +
7
_
.
Asadar:
inf A
= min A
=
2
7
, sup A
= max A
=
2 +
7
.
1.31 Sa se determine minorant ii, majorant ii, cel mai mic element si cel mai mare
element (daca exista) ale urmatoarelor mult imi de numere reale:
1) A = sin 1, sin 2, sin 3. 2) A =
_
1
1
n
, n N
_
.
3) A =
_
2
n
1
2
n
+1
, n N
_
. 4) A = x R, x
2
5.
5) A = x R, x 0, x
2
> 5. 6) A = x R, x
3
x 0.
7) A = x sin x, x R.
R: 1) Cum: sin 2 = sin(2), sin 3 = sin(3), deoarece: 0 < 3 < 1 < 2 <

2
si funct ia sinus este strict crescatoare pe
_
0,

2
, rezulta:
sin 0 < sin( 3) < sin 1 < sin( 2) < sin

2
si deci 0 < sin 3 < sin 1 < sin 2 < 1. Asadar: min A = sin 3, max A = sin 2 si orice numar
a sin 3 este un minorant, iar orice numar b sin 2 este un majorant.
2) Deoarece
1
n
1, rezulta ca 1
1
n
0. Deci 0 este un minorant al mult imii A si
orice numar a (, 0] este minorant. Nici un numar a > 0 nu poate minorant al
mult imii A deoarece 0 A si din denit ia minorantului ar rezulta ca a 0 (contradict ie).
Evident inf A = min A = 0. Mult imea majorant ilor este [1, ).

Intr-adevar, b 1
implica b 1
1
n
, pentru orice n N
. Daca b < 1 rezulta 1 b > 0 si atunci n N
a.. 1 b >
1
n
sau b < 1
1
n
, adica b nu ar mai majorant. Evident sup A = 1, n timp
ce max A nu exista.
3) Din inegalitatea:
1
3

2
n
1
2
n
+ 1
< 1, n N
,
deducem ca mult imea miniorant ilor lui A este
_
,
1
3
, mult imea majorant ilor este

[1, ), inf A = min A =
1
3
, sup A = 1, iar max A nu exista.
4) inf A = min A =
5, sup A = max A =
5,
5) inf A =
5, sup A = , 6) inf A = , max A = sup A = 1,

7) inf A
7
= , sup A
7
= .
1.32 Sa se determine inf A, min A, sup A si max A daca:
1) A = x R, x =
a+1
a
2
+a+1
, a R.
2) A = y R, y =
x
2
3x+2
x
2
+x+1
, x R.
3) A = y R, y =
3x
2
+4x
31
x
2
+1
, x R.
R: 1) Din xa
2
+ (x 1)a + x 1 = 0, cu a R, rezulta A =
_
1
3
, 1
. Deci
inf A = min A =
1
3
, sup A = max A = 1. 2) A =
_
92
21
3
,
9+2
21
3
_
. 3) A = [3, 5].
1.33 Utilizand axioma lui Arhimede, sa se arate ca pentru orice x R
exista n Z
a.. sa avem:
1) x
2
+n nx + 1. 2) x
2
2x +n.
R: 1) Inegalitatea se mai scrie: x
2
1 n(x 1). Pentru x = 1 este evidenta. Daca
x ,= 1, pentru numarul real
x
2
1
x1
= x + 1, conform axiomei lui Arhimede, exista n Z
a.. x + 1 n.
1.34 Fie [a
n
, b
n
] [a
n+1
, b
n+1
], n N
un sir descendent de segmente reale. Sa se

arate ca:
1)
n=1
[a
n
, b
n
] ,= (Cantor-Dedekind).
2) Daca b
n
a
n

1
n
, n N
, atunci exista un numar x

0
R, unic determinat, cu
proprietatea ca:
n=1
[a
n
, b
n
] = x
0
.
R: 1) Din [a
n
, b
n
] [a
n+1
, b
n+1
] rezulta ca a
n
b
m
, n, m N
. Asadar mult imea

A = a
n
, n N
este marginita superior (orice b

m
este un majorant), iar mult imea
B = b
m
, m N
este marginita inferior (orice a

n
este un minorant). Exista deci sup A
si inf B si sup A inf B.

In concluzie,
n=1
[a
n
, b
n
] [sup A, inf B] ,= .
2) Daca ar exista x si y cu x < y si x, y
n=1
[a
n
, b
n
], atunci din a
n
x < y b
n
rezulta: 0 < y x b
n
a
n

1
n
, adica n(y x) 1, n N
, ceea ce ar contrazice
axioma lui Arhimede aplicata numerelor y x si 1.
1.35 Daca a
1
, a
2
, . . . , a
n
R
+
si a
1
a
2
a
n
= 1, atunci a
1
+a
2
+ +a
n
n.
R: Folosim metoda induct iei matematice. P(2) : daca a
1
, a
2
R
+
si a
1
a
2
= 1, atunci
a
1
+a
2
2. Fie a
1
1 si a
2
1. Urmeaza (a
1
1)(a
2
1) 0 sau a
1
+a
2
1+a
1
a
2
2.
P(n) : daca a
1
, a
2
, . . . , a
n
R
+
si a
1
a
2
a
n
= 1, atunci a
1
+a
2
+ +a
n
n.
P(n + 1) : daca a
1
, a
2
, . . . , a
n
, a
n+1
R
+
si a
1
a
2
a
n
a
n+1
= 1, atunci
a
1
+a
2
+ +a
n
+a
n+1
n + 1.
Printre numerele a
1
, a
2
, . . . , a
n
, a
n+1
exista cel put in unul mai mare sau cel put in egal
cu 1 si cel put in unul mai mic sau cel mult egal cu 1. Fara a restrange generalitatea,
putem presupune ca acestea sunt a
1
si a
2
. Din P(2) avem ca a
1
+ a
2
1 + a
1
a
2
, de
unde deducem:
a
1
+a
2
+ +a
n
+a
n+1
1 +a
1
a
2
+a
3
+ +a
n
+a
n+1
1 +n,
deoarece a
1
a
2
, . . . , a
n
, a
n+1
sunt n numere al caror produs este 1.
1.36 Inegalitatea mediilor. Fie x
1
, x
2
, . . . , x
n
R
+
si A media aritmetica, G media
geometric a, H media armonica a celor n numere, denite prin;
A =
x
1
+x
2
+ +x
n
n
, G =
n
x
1
x
2
x
n
, H =
n
1
x
1
+
1
x
2
+
1
x
n
.
Sa se arate ca au loc inegalitat ile: H G A.
R: Din denit ia mediei geometrice avem:
x
1
x
2
x
n
G
n
= 1 sau
x
1
G

x
2
G

x
n
G
= 1.
Luand n exercit iul precedent a
k
=
x
k
G
, k = 1, n, obt inem:
x
1
G
+
x
2
G
+ +
x
n
G
n, sau
A G.

Inlocuind aici pe x
k
prin
1
x
k
, k = 1, n, gasim H G.
1.37 Inegalitatea lui Schwarz-Cauchy. Pentru orice numere reale a
1
, a
2
, . . . , a
n
si
b
1
, b
2
, . . . , b
n
are loc inegalitatea:
(a
1
b
1
+a
2
b
2
+ +a
n
b
n
)
2
_
a
2
1
+a
2
2
+ +a
2
n
_ _
b
2
1
+b
2
2
+ +b
2
n
_
,
sau
k=1
a
k
b
k
_
n
k=1
a
2
k
_
n
k=1
b
2
k
.
R: Fie trinomul de gradul al doilea:
f(x) =
_
a
2
1
+a
2
2
+ +a
2
n
_
x
2
2 (a
1
b
1
+a
2
b
2
+ +a
n
b
n
) x +
_
b
2
1
+b
2
2
+ +b
2
n
_
,
care se mai scrie:
f(x) = (a
1
x b
1
)
2
+ (a
2
x b
2
)
2
+ + (a
n
x b
n
)
2
0
pentru orice x R, deci 0, ceea ce implica inegalitatea data.
1.38 Inegalitatea lui Minkowski. Pentru orice numere reale a
k
, b
k
, k = 1, n are loc
inegalitatea:
_
n
k=1
(a
k
+b
k
)
2
_
n
k=1
a
2
k
+
_
n
k=1
b
2
k
.
R: Tinand seama de inegalitatea lui Schwarz-Cauchy, avem:
n
k=1
(a
k
+b
k
)
2
=
n
k=1
a
2
k
+ 2
n
k=1
a
k
b
k
+
n
k=1
b
2
k

n
k=1
a
2
k
+ 2
_
n
k=1
a
2
k
_
n
k=1
b
2
k
+
n
k=1
b
2
k
,
sau
n
k=1
(a
k
+b
k
)
2
_
_
_
n
k=1
a
2
k
+
_
n
k=1
b
2
k
_
_
2
,
de unde, extragand radicalul rezulta inegalitatea data.
1.39 Inegalitatea lui Bernoulli. Oricare ar a [1, ) si [1, ) avem:
(1 +a)
1 +a.
R: Inegalitatea rezulta din studiul monotoniei funct iei f : [1, ) R, f(x) =
(1 +x)
x 1, observand ca aceasta are un minim egal cu 0 n x = 0.

1.40 Daca a [1, ) si n N
atunci: (1 +a)
n
1 +na.
R: Se ia n inegalitatea lui Bernoulli = n.
1.41 Daca b > 0, b ,= 1, atunci:
_
1+nb
n+1
_
n+1
> b
n
.
R: Aplicand inegalitatea lui Bernoulli, avem:
_
1 +nb
n + 1
_
n+1
=
_
b +
1 b
n + 1
_
n+1
= b
n+1
_
1 +
1 b
b(n + 1)
_
n+1
> b
n+1
_
1 +
1 b
b
_
= b
n
.
1.42 Sa se arate ca:
1)
_
1 +
1
n + 1
1
_
n+1
>
_
1 +
1
n
_
n
. 2)
_
1
1
n + 1
_
n+1
>
_
1
1
n
_
n
.
R: Se ia n inegalitatea precedenta b = 1 +
1
n
, respectiv b = 1 +
1
n
.
1.43 Sa se arate ca oricare ar numerele reale a
1
, a
2
, . . . , a
n
1, de acelasi semn,
are loc inegalitatea (generalizare a inegalitat ii lui Bernoulli):
(1 +a
1
)(1 +a
2
) (1 +a
n
) 1 +a
1
+a
2
+ +a
n
.
R: Se foloseste induct ia matematica.
1.44 Inegalitatea lui Cebsev. Fie a
1
, a
2
, . . . , a
n
si b
1
, b
2
, . . . , b
n
numere reale cu
a
1
a
2
a
n
, b
1
b
2
b
n
si S = a
1
b
i
1
+ a
2
b
i
2
+ a
n
b
i
n
, n 2, unde
i
1
, i
2
, . . . , i
n
= 1, 2, . . . , n. Sa se arate ca:
a
1
b
n
+a
2
b
n1
+ a
n
b
1
S a
1
b
1
+a
2
b
2
+ +a
n
b
n
.
R: Fie j < k, i
j
< i
k
atunci (a
j
a
k
)(b
i
j
b
i
k
) 0 implica: a
j
b
i
j
+a
k
b
i
k
a
j
b
i
k
+
a
k
b
i
j
. Deci orice inversiune n mult imea i
1
, i
2
, . . . , i
n
micsoreaza suma S, ca atare
ea este maxima pentru permutarea identica 1, 2, . . . , n si minima pentru permutarea
n, n 1, . . . , 1.
1.45 Fie a
1
, a
2
, . . . , a
n
si b
1
, b
2
, . . . , b
n
numere reale cu a
1
a
2
a
n
, b
1
b
2

b
n
. Sa se arate ca:
n
_
n
i=1
a
i
b
i
_
_
n
i=1
a
i
_
_
n
i=1
b
i
_
.
R: Din exercit iul precedent rezulta ca max S =
n
i=1
a
i
b
i
. Avem deci inegalitat ile:
n
i=1
a
i
b
i
= a
1
b
1
+a
2
b
2
+ +a
n
b
n
,
n
i=1
a
i
b
i
a
1
b
2
+a
2
b
3
+ +a
n
b
1
,
.....................
n
i=1
a
i
b
i
a
1
b
n
+a
2
b
1
+ +a
n
b
n1
.
Prin adunare membru cu membru obt inem inegalitatea din enunt .
1.46 Fie a, b, c > 0. Sa se arate ca:
1)
a
b+c
+
b
a+c
b +
c
a+b
c
3
2
. 2) a +b +c
a
2
+b
2
2c
+
b
2
+c
2
2a
+
c
2
+a
2
2b

a
3
bc
+
b
3
ca
+
c
3
ab
.
R: Se aplica inegalitatea lui Cebsev:
1) pentru tripletele (a, b, c) si
_
1
b+c
,
1
a+c
,
1
a+b
_
,
2) pentru tripletele: (a
2
, b
2
, c
2
) si
_
1
c
,
1
b
,
1
a
_
, respectiv (a
3
, b
3
, c
3
) si
_
a
abc
,
b
abc
,
c
abc
_
.
1.47 Inegalitatea lui Holder. Daca a
1
, a
2
, . . . , a
n
0, b
1
, b
2
, . . . , b
n
0, p > 1,
q > 1 si
1
p
+
1
q
= 1, atunci:
n
i=1
a
i
b
i

_
n
i=1
a
p
i
_
1/p
_
n
i=1
b
q
i
_
1/q
.
R: Daca
n
i=1
a
p
i
= 0 sau
n
i=1
b
q
i
= 0 inegalitatea este evidenta. Fie:
A =
a
p
i
n
i=1
a
p
i
, B =
b
q
i
n
i=1
b
q
i
si funct ia f : [0, ) R, denita prin: f(x) = x
x, (0, 1). Deoarece f are n

x = 1 un maxim egal cu 1 , rezulta ca: x
x 1 , x [0, ). Luam x =
A
B
si =
1
p
, deci 1 =
1
q
, deducem: A
1
p
B
1
q
A
p
+
B
q
.

Inlocuind aici A si B, sumand
apoi dupa i de la 1 la n, obt inem inegalitatea din enunt .
1.48 Sa se arate ca pentru orice n N
are loc inegalitatea:

1
2
3
3!
N
n!
(n + 1)!
2
n
.
R: Se foloseste majorarea:
k
k! =
k
1 2 k
1+2++k
k
=
k+1
k
.
1.49 Daca x
1
, x
2
, . . . , x
n
R
+
, atunci:
(x
1
+x
2
+ +x
n
)
_
1
x
1
+
1
x
2
+ +
1
x
n
_
n
2
.
R: Se foloseste inegalitatea lui Schwarz-Cauchy cu a
i
=
x
i
, b
i
=
1
x
i
, i = 1, n.
1.50 Daca a
1
, a
2
, . . . , a
n
R
+
, atunci:
(a
2
1
+a
1
+ 1) (a
2
n
+a
n
+ 1)
a
1
a
2
a
n
3
n
.
R: Se foloseste inegalitatea: x +
1
x
2, pentru orice x R
+
.
1.51 Daca a
1
, a
2
, . . . , a
n
R
+
, n 2 si S = a
1
+a
2
+ +a
n
atunci:
a
1
S a
1
+
a
2
S a
2
+ +
a
n
S a
n
n
n 1
.
R: Notam b
i
=
1
Sa
i
1, i = 1, n. Deoarece S > a
i
rezulta ca b
i
> 0. putem scrie:
(b
1
+b
2
+ +b
n
)
_
1
b
1
+
1
b
2
+ +
1
b
n
_
n
2
,
sau
n
2
n 1

_
n
k=1
a
k
__
n
k=1
b
k
_
n
_
a
1
S a
1
+
a
2
S a
2
+ +
a
n
S a
n
_
.
1.52 Daca a, b, c R
+
, atunci:
ab
a +b
+
bc
b +c
+
ca
c +a

a +b +c
2
.
R: Se t ine seama ca
ab
a+b

a+b
4
etc.
1.53 Daca a
1
, a
2
, . . . , a
n
R
+
, n 2, atunci:
a
1
a
2
+
a
2
a
3
+ +
a
n1
a
n
+
a
n
a
1
n.
R: Se foloset e inegalitatea mediilor.
1.54 Daca a
1
, a
2
, . . . , a
n
R
+
, atunci:
(1 +a
1
)(1 +a
2
) (1 +a
n
) 2
n
.
R: Se nmult esc membru cu membru inegalitat ile: 1 +a
i
2
a
i
, i = 1, n.
1.55 Daca a, b, c R
+
, atunci: (a +b)(b +c)(c +a) 8abc.
R: Se nmult esc membru cu membru inegalitat ile: a +b 2
ab etc.
1.56 Daca a
1
, a
2
, . . . , a
n
> 0, b
1
, b
2
, . . . , b
n
> 0, atunci:
n
_
(a
1
+b
1
)(a
2
+b
2
) (a
n
+b
n
)
n
a
1
a
2
a
n
n
_
b
1
b
2
b
n
.
R: Se foloseste inegalitatea mediilor pentru numerele:
a
i
a
i
+b
i
, i = 1, n si respectiv:
b
i
a
i
+b
i
, i = 1, n si se aduna inegalitat ile obt inute.
1.57 Daca a, b, c R
+
, atunci:
a
a
b
b
c
c
(abc)
a+b+c
3
.
R: Fara a restrange generalitatea, putem presupune a b c. Din a
ab
b
ab
,
b
bc
c
bc
, a
ac
c
ac
prin nmult ire membru cu membru se obt ine inegalitatea din
enunt .
Capitolul 2
Siruri si serii
2.1 Siruri de numere reale
2.1 Folosind teorema de caracterizare cu a limitei unui sir, sa se arate ca:
1) lim
n
3 4
n
+ (4)
n
5
n
= 0. 2) lim
n
n
2
+ 2
n + 1
= +.
R: 1) Fie > 0 arbitrar. Este sucient sa aratam ca exista un rang N = N() a..
3 4
n
+ (4)
n
5
n
0
< , n > N.
Dar
34
n
+(4)
n
5
n

44
n
5
n
< pentru n >
ln

4
ln
4
5
. Asadar, putem lua
N() =
_
0, > 4,
_
ln

4
ln
4
5
_
, 4.
2) Fie > 0 arbitrar. Este sucient sa aratam ca exista un rang N = N() a..
n
2
+2
n+1
> , n > N.

Insa
n
2
+2
n+1
= n 1 +
3
n+1
> n 1 > , pentru n > 1 +. Putem lua
N() = [1 +].
2.2 Folosind teorema de caracterizare cu a limitei unui sir, sa se arate ca:
1) lim
n
n
2n 1
=
1
2
. 2) lim
n
4n + 1
5n 1
=
4
5
. 3) lim
n
n
2
2(n
2
+ 1)
=
1
2
.
2.3 Folosind criteriul lui Cauchy, sa se arate ca sirurile (x
n
)
nN
sunt convergente,
unde:
1) x
n
=
n
k=1
1
k
2
. 2) x
n
=
n
k=1
sin(kx)
2
k
, x R.
3) x
n
=
n
k=1
k
a
k
. [
k
[ < 1, k N
, a > 1.
16
CAPITOLUL 2. SIRURI SI SERII 17
R: 1) Aratam ca > 0, N() a.. [x
n+p
x
n
[ < , n > N() si p N
. Deoarece
1
(n +k)
2
<
1
(n +k) (n +k 1)
=
1
n +k 1

1
n +k
,
avem:
[x
n+p
x
n
[ =
1
(n + 1)
2
+ +
1
(n +p)
2
<
1
n

1
n +p
<
1
n
<
pentru n >
1
. Putem lua N() =

_
1
.
2) Aratam ca > 0, N() a.. [x
n+p
x
n
[ < , n > N() si p N
. Avem:
[x
n+p
x
n
[ =
sin(n + 1)x
2
n+1
+ +
sin(n +p)x
2
n+p
1
2
n+1
+ +
1
2
n+p
=
1
2
n
_
1
1
2
p
_
,
deci [x
n+p
x
n
[ <
1
2
n
< pentru n >
ln
1
ln 2
. Putem lua N() =
_
ln
1
ln 2
_
.
3) Avem
[x
n+p
x
n
[ =
n+1
a
n+1
+ +

n+p
a
n+p

[
n+1
[
a
n+1
+ +
[
n+p
[
a
n+p
<
1
a
n+1
+ +
1
a
n+p
,
deci [x
n+p
x
n
[ <
1
a
n
(a1)

_
1
_
1
a
_
p
<
1
a
n
(a1)
1 < pentru n >
ln
1
(a1)
ln a
. Putem lua
N() =
_
ln
1
(a1)
ln a
_
.
2.4 Folosind criteriul lui Cauchy, sa se arate ca sirul (x
n
)
nN
este divergent, unde
x
n
= 1 +
1
2
+
1
3
+ +
1
n
.
R: Este sucient sa aratam ca exista un
0
> 0 si un p N
a.. [x
n+p
x
n
[
0
.
Se constata nsa imediat ca pentru p = n avem:
[x
2n
x
n
[ =
1
n + 1
+ +
1
2n

1
2
=
0
.
2.5 Sa se cerceteze natura urmatoarelor siruri (x
n
)
nN
cu termenii generali:
1) x
n
=
10
1
+
11
3
+ +
n + 10
2n + 1
. 2) x
n
= sin n.
R: 1) Sirul este divergent. Se observa ca:
[x
2n
x
n
[ =
n + 11
2n + 3
+ +
2n + 10
4n + 1
>
2n + 10
4n + 1
>
1
2
.
2) Presupunem ca exista limx
n
= x. Atunci avem si limx
n+1
= x, limx
n1
= x,
ceea ce implica:
lim
n
[sin(n + 1) sin(n 1)] = 0,
adica lim2 sin 1 cos n = 0 sau limcos n = 0. Din sin 2n = 2 sin ncos n ar rezulta ca
limsin 2n = 0. Dar sirul (sin 2n)
nN
este un subsir al sirului (sin n)

nN
, de unde se
deduce ca limsin n = 0. Asadar am avea: lim
_
sin
2
n + cos
2
n
_
= 0. Contradict ie. Deci
sirul (x
n
) este divergent.
2.6 Folosind criteriul lui Cauchy, sa se studieze natura sirurilor cu termenii generali:
1) x
n
=
n
k=1
cos k!
k (k + 1)
. 2) x
n
=
n
k=1
cos kx
a
k
, a > 1. 3) x
n
=
n
k=1
sin kx
3
k
.
2.7 Sa se calculeze limita sirului cu termenul general:
x
n
=

0
n
k
+
1
n
k1
+ +
k
0
n
h
+
1
n
h1
+ +
h
,
0
,
0
,= 0, k, h N.
2.8 Sa se calculeze limitele sirurilor:
1) x
n
=
1 + 2 + +n
n
2
. 2) x
n
=
C
k
n
n
k
. 3) x
n
=
n
2
n
.
2.9 Sa se arate ca daca [a[ < 1, atunci limna
n
= 0.
R: Deoarece [a[ < 1, exista b > 0 a.. [a[ =
1
1+b
si se dezvolta dupa binomul lui
Newton.
2.10 Fie x
1
, x
2
, . . . , x
p
numere reale pozitive. Sa se arate ca:
lim
n
n
_
x
n
1
+x
n
2
+ x
n
p
= maxx
1
, x
2
, . . . , x
p
.
R: Fie x = maxx
1
, x
2
, . . . , x
p
. Rezulta: x
n
x
n
1
+x
n
2
+ x
n
p
px
n
, adica;
x
n
_
x
n
1
+x
n
2
+ x
n
p
x
n
p.
Dar lim
n
p = 1.
2.11 Fie sirul cu termenul general:
x
n
= a +n + 1
n
k=1
k
4
+k
2
+ 1
k
4
+k
.
1) Sa se arate ca (x
n
) este convergent.
2) Sa se gaseasca rangul de la care [x
n
a[ 0, 01.
2.12 Sa se calculeze limitele sirurilor (x
n
) date prin termenii generali:
1) x
n
=
5n
2
3n + 2
4n + 1
. 2) x
n
=
_
3n + 2
3n + 5
_
n
. 3) x
n
=
2a
n
+b
n
3a
n
+ 4b
n
.
4) x
n
=
2
2
+ 4
2
+ + (2n)
2
1
2
+ 3
2
+ + (2n 1)
2
. 5) x
n
=
n + 1 2
n + 2 +
n + 3.
6) x
n
=
_
n + 2
n + 1
_
n + 4
n + 1. 7) x
n
=
3
_
n
2
+n + 1 an.
8) x
n
=
_
2n
2
+ 5n + 4
3n
2
+ 2
_
6n
3n+1
. 9) x
n
=
_
n +
n + 1
n +
3
n + 2
_
n
. 10) x
n
=
_
1 +
1
n
_
3
1
_
3 +
1
n
_
2
9
.
11) x
n
=
n(1
3
+ 2
3
+ +n
3
)
(n + 2)
5
. 12) x
n
=
_
n
4
+n
2
+ 1
_
n
4
n
2
+ 1.
13) x
n
= n
k
_
_
n + 2
n + 5
1
_
. 14) x
n
= n
1
3
_
3
_
(n + 1)
2
3
_
(n 1)
2
_
.
2.13 Se considera curba formata din semicercuri de raze r,
r
3
,
r
9
,
r
27
, . . . cu centrele cer-
curilor coliniare. Sa se calculeze lungimea L
n
a liniei formate din primele n semicercuri,
precum si L = limL
n
. Care sunt valorile lui n pentru care diferent a L L
n
reprezinta
cel mult 5% din L ?
R: Avem:
L
n
=
_
r +
r
3
+
r
3
2
+ +
r
3
n1
_
=
3r
2

_
1
1
3
n
_
si L =
3r
2
. L L
n
=
3r
2

1
3
n

5
100

3r
2
, de unde 3
n
20, adica n 3.
2.14 Sa se discute dupa valorile parametrului real p:
= lim
n
n
p
_
_
n + 1
n + 2

3
_
n + 2
n + 3
_
.
R: Notam
a
n
=
_
n + 1
n + 2

3
_
n + 2
n + 3
=
_
_
n + 1
n + 2
1
_
+
_
1
3
_
n + 2
n + 3
_
.
Avem a
n
0, iar na
n

1
6
. Deci:
=
1
6
lim
n
n
p1
=
_
_
_
0, p (, 1),
1
6
, p = 1,
, p (1, ).
2.15 Sa se calculeze limita sirului (x
n
) cu termenul general:
x
n
=
sin 1 +a sin 2 + +a
n1
sinn
a
n
[1 + 2a + 3a
2
+ + (n + 1)a
n
]
, a > 1.
R: Din [sin x[ 1, x R, deducem:
0 < [x
n
[
(1 a)(1 a
n
)
a
n
[1 (n + 2)a
n+1
+ (n + 1)a
n+2
]
=
n
si cum pentru a > 1,
n
0, rezulta ca x
n
0.
2.16 Sa se arate ca sirul cu termenul general x
n
= 1+
1
1!
+
1
2!
+ +
1
n!
este convergent.
Limita sa este numarul e.
R: Folosim criteriul lui Cauchy:
x
n+p
x
n
=
1
(n + 1)!
+
1
(n + 2)!
+ +
1
(n +p)!
=
=
1
(n + 1)!
_
1
n + 1
+
1
(n + 1)(n + 2)
+ +
1
(n + 1)(n + 2) (n +p)
_
de unde:
x
n+p
x
n
<
1
n!
_
1
n + 1
+
1
(n + 1)
2
1 + +
1
(n + 1)
p
_
<
1
n!

1
n

1
n
< ,
pentru n > N() =
_
1
.
2.17 Sa se arate ca daca a
n
a, atunci s
n
=
a
1
+a
2
++a
n
n
a.
R: Se aplica teorema lui Stolz-Cesaro.
2.18 Sa se arate ca daca sirul de numere pozitive b
n
b, atunci
p
n
=
n
_
b
1
b
2
b
n
b.
2.19 Fie (a)
n
un sir de numere pozitive. Sa se arate ca daca
lim
n
a
n+1
a
n
= lim
n
n
a
n
= .
R: Se t ine seama de egalitatea
n
a
n
=
n
_
a
1
1

a
2
a
1

a
n
a
n1
.
2.20 Sa se calculeze:
1) lim
n
n
n. 2) lim
n
n
_
(n + 1)(n + 2) (2n)
n
n
. 3) lim
n
n
n!
n
.
R: Se aplica exercit iul precedent. Se obt ine: 1) 1, 2)
4
e
, 3)
1
e
.
lim
n
1
p
+ 2
p
+ n
p
n
p+1
=
1
p + 1
, p N.
R: Se aplica teorema lui Stolz-Cesaro:
a
n+1
a
n
b
n+1
b
n
=
(n + 1)
p
(n + 1)
p+1
n
p+1
=
_
1 +
1
n
_
p
n
__
1 +
1
n
_
p
1
+
_
1 +
1
n
_
p
.
Dar limn
__
1 +
1
n
_
p
1
= p.
2.22 Sa se determine limita sirului cu termenul general:
x
n
=
1
p
+ 3
p
+ + (2n 1)
p
n
p+1
, p N
.
lim
n
1 +
2! +
3
3! + +
n
n!
n
2
a
n
, a > 1.
lim
n
a
n+1
a
n
b
n+1
b
n
= lim
n
n+1
_
(n + 1)!
a
n
[(n + 1)
2
a n
2
]
=
1
a 1
lim
n
n+1
_
(n + 1)!
n + 1

n + 1
n
2
a
n
= 0.
lim
n
1 + (2!)
2
2 + (3!)
2
3 + + (n!)
2
n
n! (n + 1)!
n
.
lim
n
a
n+1
a
n
b
n+1
b
n
= lim
n
(n + 1)
n+1
n + 1
(n + 1)(n + 2)
n + 1
n
= 0.
2.25 Se da sirul (x
n
)
nN
cu termenul general:
x
n
=
n
k=0
1
(k + 1)(k + 4)
.
1) Sa se arate ca sirul este marginit si sa se calculeze sup x
n
.
2) Sa se calculeze lim
_
18
11
x
n
n
.
R: 1) Din identitatea
1
(k + 1)(k + 4)
=
1
3
_
1
k + 1

1
k + 4
_
, k N,
deducem:
lim
n
x
n
= lim
n
1
3
_
11
6

1
k + 2

1
k + 3

1
k + 4
_
=
11
18
.
Din x
n+1
x
n
=
1
(n+2)(n+5)
> 0 rezulta ca sirul este crescator si deci sup x
n
=
11
18
.
2) lim
_
18
11
x
n
n
= e
1
.
2.26 Sa se determine limita urmatoarelor siruri:
1) x
n
=
3
1
3
+
5
1
3
+ 2
3
+ +
2n + 1
1
3
+ 2
3
+ +n
3
. 2) x
n
=

n
+
n
n+1
+
n+1
, , > 0.
3) x
n
=
a
n
+b
n
+ 3
n
2
n
+ 5
n
+n
, a, b 0. 4) x
n
=
1
7
n
n!

n
k=1
_
k
2
+ 3k + 9
_
.
R: La 4) se t ine seama de inegalitatea k
2
+ 3k + 9 3
3
27k
3
= 9k.
2.27 Sa se calculeze limita urmatoarelor siruri:
1) x
n
=
n
(n!)
2
(2n)! 8
n
. 2) x
n
=
n
k=1
k
2
+k 1
(k + 1)!
. 3) x
n
=
n
k=1
2
k1
(k 1)
(k + 1)!
.
4) x
n
=
n
3
3n
(n!)
3
(3n)!
. 5) x
n
=
n
k=1
1
n
2
+k
. 6) x
n
=
n
k=1
_
3
_
1 +
k
2
n
3
1
_
.
R: 1) lim
a
n+1
a
n
= lim
n+1
16(2n+1)
=
1
32
. 2) Din
k
2
+k1
(k+1)!
=
1
(k1)!

1
(k+1)!
deducem ca
lim
n
n
k=1
k
2
+k 1
(k + 1)!
= lim
n
_
2
1
n!

1
(n + 1)!
_
= 2.
3) Din
2
k1
(k1)
(k+1)!
=
2
k1
k!

2
k
(k+1)!
deducem ca
lim
n
n
k=1
2
k1
(k 1)
(k + 1)!
= lim
n
_
1
2
n
(n + 1)!
_
= 1.
2.28 Sa se calculeze limitele sirurilor cu termenii generali:
1) x
n
=
(2n + 1)!!
(2n + 2)!!
. 2) x
n
=
n
k=1
k
2
+k
n
3
+k
. 3) x
n
=
n
k=1
k
2
+k 1
(k + 1)!
.
4) x
n
=
_
1 +
1
2
+
1
2
2
+ +
1
2
n
_
3 2
n
+ (1)
n
2
n
. 5) x
n
=
n
k=1
2k + 1
k
2
(k + 1)
2
.
6) x
n
=
1
n
2

_
_
C
2
n
+
_
C
2
n+1
+ +C
2
2n
_
. 7) x
n
=
1
n
3

_
n
k=1
(2k 1)
2
_
.
2.29 Sa se calculeze limita sirurilor cu termenii generali:
1) x
n
=
_
cos

n
_
n
2
. 2) x
n
=
_
1 +
3
n + 1
2
n 3
_
n3
, R.
3) x
n
=
n
k=1
1
(k 1)! +k!
. 4) x
n
=
n
k=1
k (k + 1) (k + 2)
n
4
.
2.30 Sa se calculeze limita sirului cu termenul general
x
n
= ac + (a +ab)c
2
+ (a +ab +ab
2
)c
3
+ + (a +ab + +ab
n
)c
n+1
,
a, b, c R, [c[ < 1, b ,= 1, [bc[ < 1.
R: Sa observam ca se mai scrie
x
n
=
ac
1 b
[(1 +c + +c
n
) b (1 +bc + +b
n
c
n
)] .
Deci
lim
n
x
n
= lim
n
x
n
_
1 c
n+1
1 c
b
1 (bc)
n+1
1 bc
_
=
ac
(1 c)(1 bc)
.
0 < ln [ln (k + 1)] ln (ln k) <
1
k ln k
, k 2
si apoi sa se calculeze lim
n
k=2
1
k ln k
.
R: Inegalitatea din stanga rezulta din faptul ca funct ia lnx este strict crescatoare.
Fie f : (1, ) R, denita prin f(x) = ln (ln x). Pe ecare interval [k, k + 1], k 2,
conform teoremei lui Lagrange, exista c
k
(k, k + 1) a..
ln [ln (k + 1)] ln (ln k) =
1
c
k
ln c
k
.
Din ln k < ln c
k
< ln(k + 1) deducem:
1
(k + 1) ln(k + 1)
<
1
c
k
ln c
k
<
1
k ln k
,
deci
0 <
1
(k + 1) ln(k + 1)
< ln [ln (k + 1)] ln (ln k) <
1
k ln k
.
Sumand pentru k = 2, n rezulta ca limita este .
x
n
=
n
_
(n
2
+ 1)(n
2
+ 2
2
) (2n
2
)
n
2
.
R: Avem ca
ln x
n
=
1
n
n
k=1
ln
_
1 +
k
2
n
2
_
,
care este o suma Riemann pentru funct ia f(x) = ln(1 + x
2
) pe intervalul [0, 1], pentru
diviziunea
n
=
_
0,
1
n
,
2
n
, . . . , 1
_
, cu punctele intermediare
k
=
k
n
si deci
lim
n
ln x
n
=
_
1
0
ln(1 +x
2
) dx = ln 2 2 +

2
.
x
n
=
_
_
b
a
(x a)
n
(b x)
n
dx
_1
n
, a < b.
R: Notam I
m,n
=
_
b
a
(x a)
m
(b x)
n
dx. Integrand prin part i, obt inem
I
m,n
=
m
n + 1
I
m1,n+1
=
m
n + 1

m1
n + 2

1
n +m+ 1
I
0,n+m
.
Se obt ine de aici ca I
n,n
=
(n!)
2
(2n+1)!
(b a)
2n+1
, de unde limx
n
=
_
ba
2
_
2
.
2.34 Sa se calculeze lim
_
n
k=1
_
1 +
k
n
2
1
_
.
R: Deoarece
_
1 +
k
n
2
1 =
1
n
2

k
1+
k
n
2
+1
. Din
1
n
2

k
_
1 +
1
n
+ 1
1
n
2

k
_
1 +
k
n
2
+ 1
1
n
2

k
_
1 +
1
n
2
+ 1
,
sumand pentru k = 1, n, rezulta
n(n + 1)
2n
2

1
_
1 +
1
n
+ 1
_
n
k=1
_
1 +
k
n
2
1
_
n(n + 1)
2n
2

1
_
1 +
1
n
2
+ 1
,
deci sirul are limita
1
2
.
2.35 Fiind data funct ia f : R 2, 1 R, denita prin f(x) =
1
x
2
+3x+2
, sa se
calculeze limita sirului cu termenul general
x
n
= f
(k)
(1) +f
(k)
(2) + +f
(k)
(n),
unde f
(k)
este derivata de ordinul k a funct iei f.
R: Deoarece f(x) se poate scrie: f(x) =
1
x+1

1
x+2
, rezulta ca
f
(k)
(x) = (1)
k
k!
_
1
(x + 1)
k+1

1
(x + 2)
k+1
_
,
si deci
x
n
=
_
1
2
k+1

1
(n + 2)
k+1
_
(1)
k
k!
1
2
k+1
.
2.36 Sa se studieze natura sirului (x
n
) denit prin: x
1
= a [1, 2] si x
n+1
= x
2
n

2x
n
+ 2, pentru n 1.
2.37 Se dau numerele reale a
0
, b
0
, c
0
. Denim sirurile (a
n
)
nN
, (b
n
)
nN
, (c
n
)
nN
prin:
a
n+1
=
1
2
(b
n
+c
n
) , b
n+1
=
1
2
(c
n
+a
n
) , c
n+1
=
1
2
(a
n
+b
n
) .
Sa se arate ca sirurile sunt convergente la
1
3
(a
0
+b
0
+c
0
).
R: Fie x
n
= a
n
+ b
n
+ c
n
. Adunand cele trei relat ii, obt inem: x
n+1
= x
n
, deci (x
n
)
este un sir constant: x
n
= x
0
. Din a
n+1
=
1
4
(a
n1
+x
0
) rezulta ca a
n

1
3
x
0
etc.
2.38 Fie q =
1
5
2
si sirul (x
n
) denit prin: x
1
= q, x
2
= 1 + q, x
n+2
= x
n
+ x
n+1
,
n N
.
1) Sa se arate ca termenii sirului sunt n progresie geometrica.
2) Sa se arate ca are loc egalitatea
n
=
x
n+2
x
n+1
x
n
x
n
x
n+2
x
n+1
x
n+1
x
n
x
n+2
= 4 x
3n+2
.
3) Sa se calculeze limx
n
.
R: 1) Prin induct ie matematica: x
2
= 1 + q = q
2
, x
3
= x
1
+ x
2
= q
3
. Presupunem
x
n
= q
n
. Din x
n+2
= x
n
+x
n+1
= q
n
+q
n+1
= q
n
(1 +q), rezulta x
n+2
= q
n+2
.
2)
n
= q
3n
(q
6
2q
3
+ 1) = 4q
3n+2
= 4x
3n+2
. 3) Deoarece [q[ < 1, limx
n
= 0.
2.39 Sa se calculeze limita sirului:
x
1
=
a, x
n+1
=
a +x
n
, a > 0.
2.40 Sa se calculeze
lim
n
_
4n 4 2a
n
_
n
, a
n
=
_
n
1
2x
2
1 +x
2
dx, n 2.
R: Se obt ine: a
n
= 2n 2 2 arctg n +

2
, iar limita este e
.
2.41 Fie (A
n
)
nN
si (B
n
)
nN
doua siruri de numere rat ionale a..:
_
a +b
k
_
n
= A
n
+B
n
k, n 1, a, b Q
+
,
k R Q.
Sa se calculeze lim
A
n
B
n
.
R: Din A
n
+B
n
k =
_
a +b
k
_
n
si A
n
B
n
k =
_
a b
k
_
n
, urmeaza:
A
n
=
1
2
__
a +b
k
_
n
+
_
a b
k
_
n
_
, B
n
=
1
2
k
__
a +b
k
_
n
_
a b
k
_
n
_
.
Asadar lim
A
n
B
n
=
k.
2.42 Fie matricea A =
_
1 0
3 2
_
si
A
n
=
_
1 0
a
n
b
n
_
, n N
.
Sa se calculeze lim
a
n
b
n
.
R: Se gaseste: a
n
= 3 (2
n
1) si b
n
= 2
n
.
2.43 Sa se calculeze limsin
2
_
n
2
+n + 1
_
.
R: Deoarece sin = sin ( n), urmeaza:
sin
2
_
_
n
2
+n + 1
_
= sin
2
_
_
n
2
+n + 1 n
_
= sin
2
_
n + 1
n
2
+n + 1 +n
_
si deci limsin
2
_
n
2
+n + 1
_
= sin
2
2
= 1.
2.44 Sa se calculeze limita sirului
x
n
=
n+1
_
(n + 1)!
n
n!, n 2.
R: Fie a
n
=
(n+1)
n
n!
. Deoarece
a
n+1
a
n
=
_
1 +
1
n+1
_
n+1
e, rezulta ca
n
a
n
= e. Fie
b
n
=
n+1
_
(n + 1)!
n
n!
=
_
n + 1
n
n!
_ 1
n+1
si b
n
n
=
_
n+1
n
n!
_ n
n+1
e si
e = lim
n
_
1 +
n+1
_
(n + 1)!
n
n!
n
n!
_
n
= lim
n
_
_
_
1 +
x
n
n
n!
_
n
n!
x
n
_
_
x
n
n
n
n!
= e
e limx
n
,
deci limx
n
=
1
e
.
2.45 Sa se determine mult imea punctelor limita, limita inferioara si limita superioara
pentru sirurile date prin:
1) x
n
=
1 + (1)
n
3
+ (1)
n
2n
3n + 1
. 2) x
n
=
_
1 +
1
n
_
n
_
(1)
n
+
1
2
_
+ cos
n
2
.
R: 1) Deoarece x
n
nN
= x
2k
kN
x
2k+1
kN
si
x
2k
=
2
3
+
4k
6k + 1

4
3
, x
2k+1
=
4k + 2
6k + 4

2
3
,
rezulta ca /=
_
2
3
,
4
3
_
, liminf x
n
=
2
3
, limsup x
n
=
4
3
.
2) Deoarece x
n
nN
= x
4k
kN
x
4k+1
kN
x
4k+2
kN
x
4k+3
kN
si
x
4k
=
3
2
_
1 +
1
4k
_
4k
+ cos 2k
3
2
e + 1,
x
4k+1
=
1
2
_
1 +
1
4k+1
_
4k+1
+ cos
(4k+1)
2

1
2
e,
x
4k+2
=
3
2
_
1 +
1
4k+2
_
4k+2
+ cos
(4k+2)
2

3
2
e 1,
x
4k+3
=
1
2
_
1 +
1
4k+3
_
4k+3
+ cos
(4k+3)
2

1
2
e,
rezulta ca /=
_
1
2
e,
3
2
e 1,
3
2
e + 1
_
, liminf x
n
=
1
2
e, limsup x
n
=
3
2
e + 1.
2.46 Sa se determine mult imea punctelor limita, limita inferioara si limita superioara
pentru sirurile date prin:
1) x
n
=
_
1 +
1
n
_
n(1)
n
n
2n + 1
+ cos
n
2
, n N
.
2) x
n
= 5 3 (1)
n(n+1)
2
+ sin
n
2
, n N.
3) x
n
=
1
n
n
(1)
n
+ sin
n
2
, n N
.
4) x
n
=
1 + (1)
n
2

n 1
n + 1
, n N.
5) x
n
= (1)
n(n+1)
2
cos
n
3
, n N.
2.2 Principiul contract iei
2.47 Sa se arate ca ecuat ia x
3
+ 4x 1 = 0 are o singura radacina reala si sa se
determine aproximat iile pana la ordinul trei ale radacinii.
R: Se constata imediat ca ecuat ia are o radacina pe intervalul [0, 1]. Scriind ecuat ia
sub forma echivalenta x =
1
x
2
+4
, problema revine la a arata ca aplicat ia : [0, 1] R,
(x) =
1
x
2
+4
, este o contract ie pe [0, 1]. Dar
d((x), (y)) = [(x) (y)[ =
[x +y[
(x
2
+ 4) (y
2
+ 4)
d(x, y)
1
8
d(x, y).
Intr-adevar, din [x[

x
2
+4
4
, deducem [x +y[ [x[ + [y[
1
4
_
x
2
+ 4
_
(y
2
+ 4). Deci
este o contract ie pe [0, 1], cu q =
1
8
. Sirul aproximat iilor succesive:
x
0
= 0, x
n+1
=
1
x
2
n
+ 4
, n = 0, 1, 2, . . .
ne da x
1
= 0, 25, x
2
= 0, 2461538, x
3
= 0, 2462695 etc.
3
+ 12x 1 = 0 are o singura radacina real a si sa se
calculeze aceasta radacin a cu o eroare mai mica de 0, 0001.
R: Se constata imediat ca ecuat ia are o radacina pe intervalul [0, 1]. Ca n exercit iul
precedent, se arata ca aplicat ia : [0, 1] R, (x) =
1
x
2
+12
, este o contract ie pe [0, 1],
cu q =
2
169
. Sirul aproximat iilor succesive este:
x
0
= 0, x
n+1
=
1
x
2
n
+ 12
, n = 0, 1, 2, . . .
Estimarea erorii metodei este data de
[x
n
[ <

1 q
q
n
, n N,
n care = [x
1
x
0
[.

In cazul nostru
[x
n
[ <
1
12
169
167
_
2
169
_
n
< 10
4
.
Se constata ca este sucient sa luam n = 2. Avem: x
0
= 0, x
1
=
1
12
= 0, 08 3333,
x
2
=
144
1729
= 0, 083285135.
2.49 Sa se arate ca ecuat ia sin x 10x + 1 = 0 are o singura radacina real a si sa se
R: Se constata imediat ca ecuat ia are o radacina pe intervalul [0, 1]. Se constata ca
aplicat ia : [0, 1] R, (x) =
1
10
(1 + sin x), este o contract ie pe [0, 1], cu q =
1
10
. Sirul
aproximat iilor succesive este:
x
0
= 0, x
n+1
=
1
10
(1 + sin x
n
) , n = 0, 1, 2, . . .
Estimarea erorii
[x
n
[ <
1
10
9
10
_
1
10
_
n
< 10
3
.
Este sucient sa luam n = 2. Avem: x
0
= 0, x
1
=
1
10
= 0, 1, x
2
=
1
10
(1 + sin 0, 1) =
0, 10998.
5
+ x
3
1, 16 = 0 are o singura rad acina reala si sa se
2.51 Fie f : [a, b] [c, c] o funct ie derivabila pe [a, b] si a.. 0 < m f
(x) M,
x [a, b]. Ce condit ie trebuie sa ndeplineasc a numarul p (m, M) pentru ca funct ia
(x) = x
1
p
f(x), x [a, b], sa e o contract ie pe [a, b] si deci ecuat ia (x) = 0 sa aiba
o singura solut ie pe [a, b]?
R: Avem: d((x), (y)) = [(x) (y)[ = [
()[ [x y[ = [
()[ d(x, y) si pentru

ca sa e contract ie este necesar sa existe q < 1 a.. [
()[ < q.

Insa
() = 1
1
p
f
(x)
si din 0 < m f
(x) M rezulta 1
M
p

() 1
m
p
< 1 (caci p (m, M)). Este
deci necesar ca 1 < 1
M
p
, adica p >
M
2
.

In concluzie, daca p (max
_
m,
M
2
_
, M),
este o contract ie pe [a, b].
Putem generaliza exercit iul precedent, presupunand p = p(x). Astfel, daca alegem
p(x) =
x x
0
f(x) f(x
0
)
, x [a, b],
se obt ine medoda coardei, iar daca alegem p(x) = f
(x) se ajunge la metoda lui Newton.

2.52 Ce condit ie trebuie sa ndeplineasca funct ia f : [a, b] R, de doua ori derivabila
pe [a, b] pentru ca funct ia (x) = x
f(x)
f
(x)
sa e o contract ie pe [a, b]?
R: Deoarece d((x), (y)) = [(x) (y)[ = [
()[ d(x, y), condit ia [
()[ q < 1
conduce la: [f(x) f
(x)[ q f
2
(x), 0 < q < 1.
2.53 Sa se calculeze aproximativ
p
a, a > 0 si p = 2, 3, . . .
R: Luam f(x) = x
p
a. Atunci (x) = x
f(x)
f
(x)
=
1
p
_
(p 1) x +ax
1p
. Cum
(x) =
p1
p
(1 ax
p
) <
p1
p
, pentru x > 0, rezulta ca este o contract ie si deci putem
lua
p
a x
n+1
=
1
p
_
(p 1) x
n
+ax
1p
n
.
2.3 Siruri n R
p
2.54 Sa se calculeze limitele urmatoarelor siruri din R
3
:
1) x
n
=
_
2n
3n 1
,
_
1 +
1
n
_
2n
,
n
_
n + 1
n 1
_
_
.
2) x
n
=
_
n
2
+ 2
n
2
+ 1
,
n
n
2
, e
1
n
_
.
2.55

In R
4
se considera sirul (x
n
) denit prin relat ia de recurent a:
6x
n+3
= 11x
n+2
6x
n+1
+x
n
, n N,
cu x
0
= (0, 0, 0, 0), x
1
= (1, 9, 3, 6), x
2
= (1, 9, 7, 8). Sa se determine x
n
si sa se calculeze
limita sirului.
R: Se cauta x
n
=
n
a, cu a R
4
. Se obt ine penrtu ecuat ia caracteristica 6
3
11
2
+ 6 1 = 0, cu radacinile: 1,
1
2
,
1
3
. Deci x
n
este de forma: x
n
= a +
1
2
n
b +
1
3
n
c.
Se obt ine limita x =
_
1
2
,
9
2
,
27
2
, 9
_
.
2.4 Serii de numere reale
2.56 Sa se arate ca seria
1
1 2
+
1
2 3
+ +
1
n(n + 1)
+ =
n=1
1
n(n + 1)
este convergenta si s = 1.
R:

In adevar,
s
n
=
1
1 2
+
1
2 3
+ +
1
n(n + 1)
=
n
k=1
_
1
k

1
k + 1
_
= 1
1
n + 1
1.
2.57 Seria
1 +
1
2
+
1
3
+ +
1
n
+ =
n=1
1
n
se numeste seria armonica, deoarece pentru n 2, a
n
este media armonica a termenilor
vecini a
n1
si a
n+1
. Sa se arate ca seria este divergenta si are suma +.
R: Sirul (s
n
) al sumelor part iale este strict crescator si divergent, deoarece
[s
2n
s
n
[ =
1
n + 1
+
1
n + 2
+ +
1
2n

1
2
,
ceea ce arata ca (s
n
) nu este sir fundamental. Deci lims
n
= +.
1 1 + 1 1 + + (1)
n1
+ =
n=1
(1)
n1
este divergenta.
R: Este o serie oscilanta deoarece sirul (s
n
) al sumelor part iale este sirul oscilant: 1,
0, 1, 0, . . ..
2.59 Seria
1 +q +q
2
+ +q
n1
+ =
n=1
q
n1
, q R
se numeste seria geometrica deoarece sirul (a
n
), a
n
= q
n1
, este o progresie geometrica
cu rat ia q. Sa se studieze natura acestei serii dupa valorile lui q.
R: Sirul sumelor part iale are termenul general
s
n
= 1 +q +q
2
+ +q
n1
=
_
1q
n
1q
, q ,= 1,
n, q = 1.
Obt inem
lim
n
s
n
=
_
1
1q
, [q[ < 1,
+, q 1.
Pentru q 1 sirul (s
n
) nu are limita. Astfel, seria geometrica cu rat ia q este convergenta
pentru [q[ < 1 si are suma
1
1q
si divergenta pentru [q[ 1.
2.60 Sa se stabileasca natura seriilor urmatoare si n caz de convergent a sa se determine
sumele lor:
1)
n=1
_
n + + 1 2
n + +
n + 1
_
, > 0.
2)
n=1
1
( +n)( +n + 1)
, R Z
.
3)
n=1
n
n
, > 1. 4)
n=1
1
15n
2
8n 3
.
5)
n=1
ln
n + 1
n
. 6)
n=1
1
n
n
.
7)
n=1
n 2
n
(n + 2)!
. 8)
n=1
2
n
[5 + (1)
n
]
n
.
R: 1) Notam cu a
n
=
n +
n + 1. Se observa ca s
n
= a
n+1
a
n
. Se obt ine
suma

+ 1.
2) Folosind identitatea:
1
( +k)( +k + 1)
=
1
+k

1
+k + 1
,
se obt ine s
n
=
1
+1

1
+n+1
. Seria este convergenta si are suma
1
+1
.
3) Pentru a evalua suma part iala de ordinul n plecam de la identitatea:
x
+
x
2
2
+ +
x
n
n
=
1
n

x
n+1
x
n
x
.
Derivand n raport cu x, avem:
1
+
2x
2
+ +
nx
n1
n
=
nx
n+1
(n + 1)x
n
+
n+1
n
(x )
2
.
De aici, pentru x = 1, obt inem
s
n
=
n (n + 1) +
n+1
n
(1 )
2
.
Seria este convergenta si are suma

(1)
2
.
4) Termenul general al sirului sumelor part iale se descompune n fract ii simple astfel:
1
16k
2
8k 3
=
1
4
_
1
4k 3

1
4k + 1
_
.
Folosind aceasta identitate se obt ine s
n
=
1
4
_
1
1
4n+1
_
. Seria este convergenta si are
suma
1
4
.
5) Sirul sumelor part iale al acestei serii
s
n
=
n
k=1
ln
k + 1
k
= ln(n + 1)
are limita , deci seria este divergenta.
6) Deoarece lim
1
n
n
= 1, seria este divergenta.
7) Fie b
n
=
2
n
(n+2)!
. Atunci termenul general al seriei se scrie a
n
= nb
n
, iar (n+2)b
n
=
2b
n1
. Deci
s
n
=
n
k=1
a
k
=
n
k=1
kb
k
= 2(b
0
b
n
) = 1 2b
n
.
Dar b
n
0 deoarece seria
n=1
2
n
(n+2)!
este convergenta. Rezulta ca seria este convergenta
si are suma 1.
8) Se observa ca:
n=1
2
n
[5 + (1)
n
]
n
=
_
1
2
+
1
2
3
+
1
2
5
+
_
+
_
1
3
2
+
1
3
4
+
1
3
6
+
_
=
19
24
.
2.61 Sa se arate ca urmatoarele serii sunt convergente si sa se determine sumele lor:
1)
n=1
(1)
n+1
3
n
. 2)
n=1
2
n
+ (1)
n+1
5
n
. 3)
n=1
1
4n
2
1
.
R: 1) Serie geometrica cu rat ia
1
3
si suma
1
4
. 2) Serie geometrica cu suma
5
6
. 3) Serie
telescopica cu suma
1
2
.
2.62 Sa se calculeze sumele urmatoarelor serii, stiind ca termenii sirului (a
n
) formeaza
o progresie aritmetica cu a
1
> 0 si rat ia r > 0:
1)
n=1
1
a
n
a
n+1
. 2)
n=1
1
a
n
a
n+1
a
n+2
. 3)
n=1
a
n
+a
n+1
a
2
n
a
2
n+1
.
R: 1) Pentru orice n N, avem:
1
a
n
a
n+1
=
1
r
_
1
a
n
1
a
n+1
_
.
Se obt ine o serie telescopica.
2) si 3) Analog, avem:
1
a
n
a
n+1
a
n+2
=
1
2r
_
1
a
n
a
n+1
1
a
n+1
a
n+2
_
,
a
n
+a
n+1
a
2
n
a
2
n+1
=
1
r
_
1
a
2
n
1
a
2
n+1
_
.
1)
n=1
3
n1
sin
3
x
3
n
=
1
4
(x sin x) . 2)
n=1
2
n
tg 2
n
x = 2 ctg 2x
1
x
.
R: 1) Multiplicam identitatea sin 3 = 3 sin 4 sin
3
cu 3
n1
si luam =
x
3
n
.
Obt inem:
3
n1
sin
3
x
3
n
=
1
4
_
3
n
sin
x
3
n
3
n1
sin
x
3
n1
_
.
Punem a
n
=
3
n1
4
sin
x
3
n1
. Atunci s
n
= a
n+1
a
1
si
lim
n
s
n
=
1
4
(x sin x) .
2) Multiplicam identitatea tg = ctg 2 ctg 2 cu 2
n
si luam = 2
n
x. Obt inem:
2
n
tg 2
n
x = 2
n
ctg 2
n
x 2
n+1
ctg 2
n+1
x.
2.64 Sa se calculeze suma seriei
n=1
arctg
1
n
2
+n + 1
.
R: Din
arctg x arctg y = arctg
x y
1 +xy
,
1
n
2
+n + 1
=
1
n

1
n+1
1 +
1
n

1
n+1
,
rezulta ca a
n
= arctg
1
n
arctg
1
n+1
si deci s
n
= arctg 1 arctg
1
n+1

4
.
p=2
n=2
1
n
p
= 1.
R: Seria
1
2
p
+
1
3
p
+ +
1
n
p
+
este convergenta pentru orice p 2, deci
p=2
n=2
1
n
p
=
n=2
p=2
1
n
p
.
Dar
p=2
1
n
p
=
1
n
2
1
1
1
n
=
1
n(n 1)
=
1
n 1

1
n
si
n=2
_
1
n 1

1
n
_
= 1 lim
n
1
n
= 1.
2.66 Sa se arate ca urmatoarele serii sunt divergente:
1)
n=1
n
2. 2)
n=1
n
n + 1
. 3)
n=1
2
n
+ 3
n
2
n+1
+ 3
n+1
.
4)
n=1
1
n + 1
n
. 5)
n=1
1
2n + 1
2n 1
.
2.67 Sa se studieze natura seriei:
n=1
a
n1
(1 +a
n1
b)(1 +a
n
b)
, a, b R
+
.
R: Deoarece termenul general al seriei se poate scrie, pentru a ,= 1:
a
n
=
1
1 a
a
n1
a
n
(1 +a
n1
b)(1 +a
n
b)
=
1
b(1 a)
(1 +a
n1
b) (1 +a
n
b)
(1 +a
n1
b)(1 +a
n
b)
,
adica
a
n
=
1
b(1 a)
_
1
1 +a
n
b

1
1 +a
n1
b
1
_
, s
n
=
1
b(1 a)
_
1
1 +a
n
b

1
1 +b
_
.
Deci
n=1
a
n1
(1 +a
n1
b)(1 +a
n
b)
=
_
_
_
1
b(a1)(b+1)
, a (1, ),
, a = 1,
1
(1a)(1+b)
, a (0, 1).
2.5 Serii cu termeni pozitivi
2.68 Fie (a
n
) un sir de numere pozitive. Sa se arate ca seria

a
n
este convergenta
d.d. seria

a
n
1+a
n
este convergenta.
R: Deoarece
a
n
1+a
n
a
n
, daca seria
a
n
este convergenta atunci si seria
a
n
1+a
n
este
convergenta.
Daca seria

a
n
1+a
n
este convergenta, atunci
a
n
1+a
n
0, deci a
n
0. Deci pentru n
sucient de mare, 0 a
n
1. Atunci
1
2
a
n

a
n
1+a
n
. Deci seria

a
n
este convergenta.
2.69 Seria
n=1
1
n
, R, numita seria lui Riemann sau seria armonica generalizata

este:
- convergenta pentru > 1;
- divergenta pentru 1.
R:

Intr-adevar, daca 0, seria este divergenta deoarece sirul termenilor ei nu
cunverge la zero.
Daca > 0, srul cu termenul general a
n
=
1
n
este descrescator si deci seria lui

Riemann are aceeasi natura cu seria
n=1
2
n
1
(2
n
)
n=1
_
1
2
1
_
n
,
care este o serie geometrica cu rat ia q = 2
1
> 0, convergenta daca q = 2
1
< 1, adica
> 1, si divergenta daca q = 2
1
1, adica 1.
2.70 Sa se arate ca seria cu termenul general a
n
=
_
n+1
2n1
_
n
este convergenta.
R: Avem:
lim
n
n
a
n
= lim
n
n
_
n + 1
2n 1
_
n
= lim
n
n + 1
2n 1
=
1
2
< 1.
n=0
1
n!
este convergent a.
R:

Intr-adevar:
a
n+1
a
n
=
n!
(n + 1)!
=
1
n + 1

1
2
< 1, n 1.
Suma acestei serii este e = 2, 7182818 . . .
n=0
2
n
(n+1)!
este convergenta si sa se precizeze numarul de
termeni necesar pentru a obt ine suma seriei cu o eroare mai mica de 0, 001.
R: Aplicam criteriul raportului cu limita
lim
n
a
n+1
a
n
= lim
n
2
n + 2
= 0 < 1,
deci seria este convergenta. Deoarece
a
n+1
a
n
=
2
n+2

1
3
, pentru n 4, restul de ordinul n
r
n
= s s
n
=
k=n+1
a
k
a
n
_
1
3
+
1
3
2
+
_
=
1
2
a
n
=
1
2

2
n
(n + 1)!
< 10
3
,
pentru n 9.
2.73 Sa se stabileasca natura seriei:
1
ln 2
+
1
3
ln 3
+ +
1
n
ln n
+
R: Deoarece
n
ln n <
n
n, pentru n 2, avem ca
1
n
ln n
>
1
n
n
. Dar seria

1
n
n
este
divergenta.
2.74 Sa se stabileasca natura seriilor:
1)
n=1
7n
n
2
+ 3n + 5
. 2)
n=1
1
n
n
n
. 3)
n=1
1
a
n
+n
, a > 1.
R: 1) Seria este convergenta. 2) Se aplica criteriul comparat iei cu limita. Se compara
cu seria

1
n
. Deoarece lim
1
n
n
= 1, seria este divergenta. 3) Pentru a > 1, cum
1
a
n
+n
<
1
a
n
, seria este convergenta. Pentru a = 1 seria data este seria armonica. Pentru
[a[ < 1 se aplica criteriul comparat iei cu limita. Se compara cu seria armonica. Deoarece
lim
n
a
n
+n
= 1, seria este divergenta.
1)
n=1
1
n(1 +a + +a
2
+a
n
)
. 2)
n=1
a
n
n
n!
, a > 0.
R: 1) Pentru a 1, 1 +a + +a
2
+a
n
n + 1 > n. Rezulta ca
1
n(1 +a + +a
2
+a
n
)
<
1
n
2
si deci seria este convergenta.
Pentru 0 < a < 1 se aplica criteriul comparat iei cu limita. Se compara cu seria
armonica. Deoarece
lim
n
1
1 +a + +a
2
+a
n
= lim
n
1 a
1 a
n+1
= 1 a,
seria data este divergenta.
2) Deoarece
n
n! 1, avem ca
a
n
n
n!
a
n
. De aici, pentru a < 1, deducem ca seria
este convergenta.
Din
n
n!
n
n
n
= n, obt inem ca
a
n
n
n!

a
n
n
. Dar, pentru a 1, seria

a
n
n
este
divergenta. Rezulta ca seria data este divergenta.
1)
n=1
1
n 2
n
. 2)
n=1
arctg
n
1
n
. 3)
n=1
n
_
1 +
1
n
_
n
2
.
R: Se aplica criteriul radacinii cu limita. Seriile sunt convergente.
1)
n=1
_
a
n
2
+n + 1
n
2
_
n
. 2)
n=1
a
n
_
1 +
1
n
_
n
.
R: Se aplica criteriul radacinii cu limita. Pentru a < 1 seriile sunt convergente, pentru
a > 1, seriile sunt divergente. Pentru a = 1, sirurile termenilor au limita e, deci seriile
sunt divergente.
n=1
a
n
_
n + 1
n
_
n
2
, a > 0.
R: Se aplica criteriul radacinii cu limita. Pentru a <
1
e
seria este convergenta, pentru
a >
1
e
, seria este divergenta. Pentru a =
1
e
, seria devine:
n=1
1
e
n
_
n + 1
n
_
n
2
.
Din e <
_
1 +
1
n
_
n+1
, obt inem:
1
e
n
_
n + 1
n
_
n
2
>
1
_
1 +
1
n
_
n
,
de unde
lim
n
1
e
n
_
n + 1
n
_
n
2
lim
n
1
_
1 +
1
n
_
n
=
1
e
> 0.
Rezulta ca seria data este divergenta.
1)
n=1
n
2
2
n
. 2)
n=1
n
2
arcsin

2
n
.
3)
n=1
n!
n
n
. 4)
n=1
ntg

2
n+1
.
R: Se aplica criteriul raportului cu limita. Seriile sunt convergente.
1)
n=1
2 7 12 (5n 3)
5 9 13 (4n + 1)
. 2)
n=1
1 3 5 (2n 1)
2 5 8 (3n 1)
.
R: Se aplica criteriul raportului cu limita. 1) Serie divergenta. 2) Serie convergenta.
1)
n=1
a
n
n!
. 2)
n=1
a
ln n
, a > 0.
R: 1) Se aplica criteriul raportului cu limita. Seria este convergenta. 2) Criteriul
raportului da dubiu. Aplicam criteriul lui Raabe-Duhamel. Se obt ine = ln a. Seria
este convergenta pentru a <
1
e
si divergenta pentru a >
1
e
. Pentru a =
1
e
se obt ine seria
armonica, deci divergenta.
2.82 Sa se studieze natura seriei cu termenul general a
n
denit astfel: a
1
(0, 1),
a
n+1
= 2
a
n
1, pentru n 1.
R: Fie f : R R, denita prin f(x) = 2
x
x 1. Deoarece f
(x) = 2
x
ln 2 1 si
f
(x) = 0 pentru x
0
= ln(ln 2), avem tabloul de variat ie:
x 0 ln(ln 2) 1
f
(x) 0 + +
f(x) 0 m 0
Deci f(x) < 0 pentru orice x (0, 1), de unde 2
x
< x + 1, x (0, 1).
Aratam, prin induct ie, ca a
n
(0, 1). Avem ca a
1
(0, 1). Presupunem ca a
n

(0, 1). Dar a
n+1
= 2
a
n
1 > 2
0
1 = 0 si a
n+1
= 2
a
n
1 < 2
1
1 = 1. Apoi:
a
n+1
a
n
= 2
a
n
a
n
1 < 0, deci este un sir descrescator si marginit. Fie = lima
n
.
Rezulta ca 2
1 = 0, cu radacinile 0 si 1. Deoarece (a
n
) este descrescator, urmeaza
ca = 0. Putem deci scrie:
lim
n
a
n+1
a
n
= lim
n
2
a
n
1
a
n
= lim
x0
2
x
1
x
= ln 2 < 1
si conform criteriului raportului seria este convergenta.
n=1
(2n + 1)
_
( 1) ( n + 1)
( + 1)( + 2) ( +n + 1)
_
2
, R Z
.
R: Criteriul raportului da dubiu. Aplicam criteriul lui Raabe-Duhamel. Deoarece
= 4a+3, daca >
1
2
seria este convergenta, daca <
1
2
seria este divergenta, daca
=
1
2
seria devine:
4
n=1
1
2n + 1
care este divergenta.
n=1
1
2
5
2
9
2
(4n 3)
2
3
2
7
2
11
2
(4n 1)
2
.
R: Criteriul raportului si criteriul lui Raabe-Duhamel dau dubiu. Aplicam criteriul
lui Bertrand:
lim
n
_
n
_
a
n
a
n+1
1
_
1
_
ln n = lim
n
ln n
16n
2
+ 8n + 1
= 0 < 1,
deci seria este divergenta.
1)
n=1
(2n)!
4
n
(n!)
2
. 2)
n=1
2 4 6 (2n)
1 3 5 (2n 1)

1
n + 2
.
3)
n=1
lg
(n + 1)
2
n(n + 2)
. 4)
n=1
_
n +
n +
_
n
, , , , > 0.
5)
n=2
1
n ln n
. 6)
n=1
1
n(ln n) ln (ln n)
.
1)
n=1
n! n
p
(q + 1) (q + 2) (q +n)
, p, q N.
2)
n=1
n!
( + 1) ( +n 1)
, > 0.
3)
n=1
cos (n) ln n
n
, R.
4)
n=1
( + 1) (2 + 1) (n + 1)
( + 1) (2 + 1) (n + 1)
, , > 0.
n=1
1
n!

a(a + 1) (a +n 1)b(b + 1) (b +n 1)
c(c + 1) (c +n 1)
,
cu a, b R, c R Z, numita seria hipergeometrica.
R:

Incepand de la un rang N care depinde de a, b si c, termenii seriei au acelasi semn
si deci putem presupune ca seria este cu termeni pozitivi. Avem:
a
n
a
n+1
= 1 +
1 +c a b
n
+

n
n
2
,
cu
n
=
[c ab (a +b) (1 +c a b)] n
3
ab (1 +c a b) n
2
n(n +a)(n +b)
.
Sirul (
n
) este convergent, deci marginit. Conform criteriului lui Gauss, pentru c > a+b
seria este convergenta, iar pentru c a +b seria este divergenta.
n=1
( + 1) ( +n 1)
( + 1) ( +n 1)
x
n
, , , x > 0.
R: Se aplica criteriul raportului cu limita. Pentru x (0, 1) seria este convergenta,
pentru x (1, ) seria este divergenta. Pentru x = 1 seria este convergenta daca
b > a + 1 si divergenta daca b a + 1.
n=1
n! b
n
(b +a
1
) (2b +a
2
) (nb +a
n
)
,
unde b > 0, iar (a
n
) este un sir de numere reale pozitive, convergent catre a cu a ,= b.
2.6 Serii cu termeni oarecare
2.90 Sa se arate ca daca

a
2
n
este o serie convergenta, atunci seria

a
n
n
este absolut
convergenta.
R: Din
_
[a
n
[
1
n
2
0 deducem ca
|a
n
|
n

1
2
_
a
2
n
+
1
n
2
_
. Deoarece

a
2
n
si

1
n
2
sunt convergente, conform primului criteriu de comparat ie rezulta ca seria

|a
n
|
n
este
convergenta.

sin nx
n
este convergenta pentru > 0.

R: Pentru > 0, sirul
n
=
1
n
este monoton descrescator la zero, iar

s
n
=
n
k=1
sin kx =
1
sin
x
2
sin
nx
2
sin
(n + 1)x
2
,
pentru x ,= 2k, cu k numar ntreg. De unde,
[s
n
[
1
[ sin
x
2
[
,
adica (s
n
) este marginit.
2.92 Sa se studieze natura seriei
n=1
cos
2n
3
x
2
+n
, x R.
R: Pentru x R, sirul
n
=
1
x
2
+n
este monoton descrescator la zero, iar
s
n
=
n
k=1
cos
2n
3
=
1
sin

3
sin
n
3
cos
(n + 1)
3
,
cu [s
n
[
2
3
, deci marginit. Seria este convergenta.
2.93 Sa se arate ca seria armonica alternata
1
1
2
+
1
3

1
4
+ +
1
2n 1

1
2n
+
este convergenta si sa se determine suma sa.
R: Sirul (
1
n
) este monoton descrescator la zero. Dupa criteriul lui Leibniz seria este
convergenta. Pentru calculul sumei folosim identitatea lui Catalan-Botez :
1
1
2
+
1
3

1
4
+ +
1
2n 1

1
2n
=
1
n + 1
+
1
n + 2
+ +
1
2n
,
care, daca notam a
n
= 1 +
1
2
+
1
3
+ +
1
n
, revine la: a
2n
2
_
a
n
2
_
= a
2n
a
n
. Rezulta
ca:
lim
n
s
n
=
1
n
_
1
1 +
1
n
+
1
1 +
2
n
+ +
1
1 +
n
n
_
=
_
1
0
dx
1 +x
= ln 2.
2.94 Sa se arate ca seria armonica generalizata (sau seria lui Riemann) alternata
n=1
(1)
n+1
1
n
n care 0 < 1 este simplu convergenta.

R: Sirul (
1
n
) cu > 0 este monoton descrescator la zero. Dupa criteriul lui Leibniz

seria este convergenta. Pentru > 1 seria este absolut convergenta.

In concluzie, pentru
0 < 1 seria lui Riemann alternata este simplu convergenta.
1)
n=1
(1)
n1
sin
1
n
. 2)
n=1
(1)
n1
arctg
1
n
.
R: Serii alternate convergente.
1)
n=1
sin
_
_
n
2
+ 1
_
. 2)
n=1
cos n
n
2
, R.
R: 1) a
n
= sin
__
n
2
+ 1 n
_
+n
= (1)
n
sin
_
n
2
+ 1 n
_
si se aplica cri-
teriul lui Leibniz.
2) Deoarece
|cos n|
n
2
<
1
n
2
, seria este absolut convergenta.
n=1
_
1 +
1
2
+ +
1
n
_
sinn
n
.
2.98 Sa se studieze convergent a absoluta si semiconvergent a seriei:
n=1
(1)
n+1
2
n
sin
2n
x
n + 1
.
R: Pentru studiul absolutei convergent e folosim criteriul radacinii. Avem:
lim
n
n
_
[a
n
[ = lim
n
2 sin
2
x
n
n + 1
= 2 sin
2
x.
Pentru 2 sin
2
x < 1 seria este absolut convergenta si deci convergenta. Pentru 2 sin
2
x = 1
obt inem seria armonica alternata care este simplu convergenta. Pentru 2 sin
2
x > 1,
termenul general al seriei nu tinde la 0, deci seria este divergenta.
2.99 Sa se efectueze produsul n sens Cauchy al seriilor absolut convergente
n=0
1
n!
,
n=0
(1)
n
1
n!
si sa se deduca de aici suma ultimei serii.
R: Seria produs
n=0
c
n
are termenul general c
n
= a
0
b
n
+a
1
b
n1
+ +a
n1
b
1
+a
n
b
0
,
adica c
0
= 1, iar, pentru n 1:
c
n
= 1
(1)
n
n!
+
1
1!

(1)
n1
(n 1)!
+
1
2!

(1)
n2
(n 2)!
+
1
(n 1)!

1
1!
+
1
n!
1 =
=
(1)
n
n!
_
1
n
1!
+
n(n 1)
2!
+ + (1)
n1
n
1!
+ (1)
n
_
=
(1)
n
n!
(1 1)
n
= 0.
Deci seria produl are suma egala cu 1. Cum
n=0
1
n!
= e, dupa teorema lui Mertens,
rezulta ca
n=0
(1)
n 1
n!
=
1
e
.
2.100 Sa se efectueze produsul n sens Cauchy al seriilor
1
n=1
_
3
2
_
n
, 1 +
n=1
_
3
2
_
n1
_
2
n
+
1
2
n+1
_
.
R: Ambele serii sunt divergente deoarece ternenii lor generali nu tind la zero. Seria
produs
n=0
c
n
are termenul general
c
n
= 1
_
3
2
_
n1
_
2
n
+
1
2
n+1
_
3
2

_
3
2
_
n2
_
2
n1
+
1
2
n
_

_
3
2
_
n
1 =
=
_
3
2
_
n1
_
2
n
_
2
n1
+ + 2
_
+
1
2
n+1
_
1
2
n
+ +
1
2
2
_
3
2
_
=
_
3
4
_
n
.
Se observa ca seria produs este convergenta, ind seria geometrica cu rat ia q =
3
4
< 1.
Rezulta de aici ca ipotezele teoremei lui Mertens sunt suciente dar nu si necesare.
Capitolul 3
Limite de funct ii
3.1 Limita unei funct ii reale de o variabila reala
1) lim
x
(x + 1)
2
x
2
+ 1
. 2) lim
x
3
x
2
+ 1
x + 1
.
3) lim
x5
x
2
7x + 10
x
2
25
. 4) lim
h0
(x +h)
3
x
3
h
.
5) lim
x0
1 +x 1
3
1 +x 1
. 6) lim
x4
3
5 +x
1
5 x
.
1) lim
x0
sin 5x
sin 2x
. 2) lim
xa
cos x cos a
x a
.
3) lim
x2
tg x
x + 2
. 4) lim
x
_
x 1
x + 1
_
x
.
5) lim
x0
(1 + sin x)
1
x
. 6) lim
x0
(cos x)
1
x
.
3.3 Sa se arate ca funct ia f : R 0 R, denita prin
f(x) =
1
x
cos
1
x
nu tinde catre innit cand x 0.
R: Pentru sirul x
n
=
1
2
+n
0, f(x
n
) = 0 si deci tinde la 0.
3.4 Sa se arate ca funct ia f : R R, denita prin f(x) = sin x, nu are limita pentru
x .
43
CAPITOLUL 3. LIMITE DE FUNCT II 44
3.5 Sa se determine R a.. funct ia f : (0, 2] R, denita prin
f(x) =
_ _
2
2xln (ex) +x
2
, x (0, 1),
+
x
e
, x [1, 2],
sa aiba limita n punctul x = 1.
3.6 Sa se arate ca:
1) lim
x
x
k
e
x
= 0. 2) lim
x
ln x
x
k
= 0, k N
.
3.7 Sa se cerceteze daca funct ia f : R R, denita prin f(x) = [x], are limita n
punctul x = 2.
1) lim
x
_
x
2
2x + 3
x
2
3x + 2
_
x+1
. 2) lim
x0
_
1 + 2 sin
2
x
_ 3
x
2
. 3) lim
x0
ln (1 + arcsin 2x)
sin 3x
.
4) lim
x0
e
sin 2x
e
sin x
sin 2x sin x
. 5) lim
x3
x
2
2x + 6
x
2
+ 2x 6
x
2
4x + 3
.
6) lim
x2
3
x
3
5x + 3
x
2
+ 3x 9
x
2
+x 6
. 7) lim
x5
x + 4
3
x + 22
4
x + 11 2
.
8) lim
x0
3
1 +x
2
1 2x
x +x
2
. 9) lim
x0
arcsin x arctg x
x
3
.
10) lim
x1
_
arcsin x

2
_
2
1 x
2
. 11) lim
x0
_
1
x
2
ctg
2
x
_
. 12) lim
x
_
x x
2
ln
x + 1
x
_
.
13) lim
x0
1 cos x
cos 2x
3
cos 3x
x
2
. 14) lim
x0
[1 + ln (1 +x) + + ln (1 +nx)]
1
x
.
15) lim
x0
_
p
1
x
1
+p
2
x
2
+ +p
n
x
n
n
_1
x
, p
i
> 0,
i
R.
16) lim
x0
_
a
sin x
+b
tg x
2
_
1
x
, a, b > 0.
R: 1) e. 2) e
6
. 3)
2
3
. 4) 1. 5)
1
3
. 6)
7
30
. 7)
112
27
. 8)
1
2
. 9)
1
2
. 10) 1.
11)
2
3
. 12) Se ia x =
1
y
, y 0, limita este
1
2
. 13) 3. 14) e
n(n+1)
2
.
15)
n
_
p
1
1
p
2
2
p
n
n
. 16)

ab.
3.9 Sa se determine parametrul real a..
lim
x
_
_
x
2
+x + 1 +
3
_
x
3
+x
2
+x + 1 ax
_
,
sa e nita si nenula.
R: Adunam si scadem x. Se obt ine a = 2 si limita egala cu
5
6
.
3.10 Sa se determine a, b, c R a..
lim
x
_
_
5x
4
+ 7x
3
8x
2
4x ax
2
bx c
_
= 0.
R: a =
5, b =
7
2
5
, c =
209
40
5
.
1) lim
x0
cos (xe
x
) cos (xe
x
)
x
3
. 2) lim
x0
1 cos x cos 2x cos nx
x
2
, n N
.
3) lim
x0
sin x
n
sin
n
x
x
n+2
, n 2. 4) lim
x0
tg x
n
ln
n
(1 +x)
x
n+1
. 5) lim
x0
_
(1 +x)
1
x
e
_1
x
.
R: 1) Se t ine seama ca cos cos = 2 sin
+
2
sin

2
si se obt ine limita 2. 2)
Notam
a
n
= lim
x0
1 cos x cos 2x cos nx
x
2
.
Avem ca a
1
=
1
2
si a
n
= a
n1
+
n
2
2
. Se obt ine a
n
=
n(n+1)(2n+1)
12
. 3) Funct ia se mai scrie
sin x
n
sin
n
x
x
n+2
=
sinx
n
x
n
x
n+2
+
x
n
sin
n
x
x
n+2
.
Se obt ine limita
n
6
. 4) Funct ia se mai scrie
tg x
n
ln
n
(1 +x)
x
n+1
=
tg x
n
x
n
x
n+1
+
x
n
ln
n
(1 +x)
x
n+1
.
Se obt ine limita
n
2
. 5)
1
e
.
1) lim
x
4
sin x
3
cos x cos x
3
sin x
ln (tg x cos 2x)
. 2) lim
x
x
2
_
e
1
x
e
1
x+1
_
.
R: 1)
3
2
6
. 2) Putem scrie
x
2
_
e
1
x
e
1
x+1
_
=
x
2
x(x + 1)
e
1
x+1
e
1
x(x+1)
1
1
x(x+1)
.
3.2 Limita unei funct ii de o variabila vectoriala
3.13 Sa se gaseasc a si sa se reprezinte grac mult imile de denit ie ale urmatoarelor
funct ii de doua variabile:
1) f (x, y) =
_
1 x
2
y
2
. 2) f (x, y) = 1 +
_
(x y)
2
.
3) f (x, y) = ln (x +y) . 4) f (x, y) = x + arccos y.
5) f (x, y) =
_
1 x
2
+
_
1 y
2
. 6) f (x, y) = arcsin
y
x
.
7) f (x, y) =
_
y sin x. 8) f (x, y) = ln
_
x
2
+y
_
.
9) f (x, y) = arctg
x y
1 +x
2
+y
2
. 10) f (x, y) =
1
_
y
x
.
11) f (x, y) =
1
x y
+
1
y
. 12) f (x, y) =
_
sin (x
2
+y
2
).
3.14 Sa se gaseasca mult imile de denit ie ale urmatoarelor funct ii de trei variabile:
1) f (x, y, z) =
x +
y +
z. 2) f (x, y, z) = arcsin x + arcsin y + arcsin z.

3) f (x, y, z) = ln (xyz) . 4) f (x, y, z) = (xy)
z
. 5) f (x, y, z) = z
xy
.
6) f (x, y, z) =
_
9 x
2
y
2
z
2
. 7) f (x, y, z) = ln
_
x
2
y
2
+z
2
1
_
.
3.15 Se da funct ia f : E R, E R
2
. Sa se arate ca:
lim
(x,y)(x
0
,y
0
)
f(x, y) =
d.d. pentru orice > 0 exista un () > 0, a.. pentru orice (x, y) E pentru care
[x x
0
[ < () , [y y
0
[ < () , [f(x, y) [ < .
R: Armat ia rezulta din dubla inegalitate:
max ([x x
0
[ , [y y
0
[) |x y| ([x x
0
[ +[y y
0
[) .
3.16 Folosind denit ia, sa se demonstreze ca:
1) lim
(x,y)(2,4)
(2x + 3y) = 16. 2) lim
(x,y)(2,3)
(4x + 2y) = 2. 3) lim
(x,y)(5,)
xy
y + 1
= 1.
4) lim
(x,y)(2,2)
x
y
= 1. 5) lim
(x,y,z)(1,2,0)
(2x + 3y 2z) = 4.
R: 1) Vom arata ca pentru orice > 0 exista un () > 0, a.. pentru orice (x, y) R
2
pentru care
[x 2[ < () , [y 4[ < () , [(2x + 3y) 16[ < .
Intr-adevar,
[(2x + 3y) 16[ = [2 (x 2) + 3 (y 4)[ 2 [x 2[ + 3 [y 3[ .
Fie > 0. Luam () =

6
. Atunci pentru [x 2[ < () si [y 4[ < ()
[(2x + 2y) 16[ < 2
6
+ 3
6
=
5
6
< .
2) Este sucient sa luam () =

7
. 3) () =

7
.
3.17 Sa se arate ca funct ia
f (x, y) =
x +y
x y
,
denita pentru x ,= y, nu are limita n origine.
R: Vom arata ca pentru siruri diferite convergente la 0, obt inem limite diferite. Fie
x
n
=
_
1
n
,
2
n
_
. Observam ca punctele x
n
sunt situate pe dreapta y = 2x si limf(x
n
) = 3.
Fie apoi x
n
=
_
1
n
,
1
n
_
. Punctele x
n
sunt situate pe dreapta y = x si limf(x
n
) = 0.
f (x, y) =
y
2
+ 2x
y
2
2x
,
denita pentru y
2
,= 2x, nu are limita n origine.
R: Vom arata ca pentru siruri diferite convergente la 0, obt inem limite diferite. Fie
x
n
=
_
1
n
,
1
n
_
. Observam ca punctele x
n
sunt situate pe parabola y
2
= x si limf(x
n
) =
3. Fie apoi x
n
=
_
1
n
,
2
n
_
. Punctele x
n
sunt situate pe parabola y
2
= 4x si limf(x
n
) =
3.
3.19 Sa se demonstreze ca
lim
(x,y)(0,0)
x
2
+y
2
[x[ +[y[
= 0.
R: Se t ine seama de inegalitat ile:
0 <
x
2
+y
2
[x[ +[y[
<
x
2
+y
2
+ 2 [x[ [y[
[x[ +[y[
< [x[ +[y[ .
f (x, y) =
x
2
y
x
4
+y
2
,
denita pentru x ,= 0 si y ,= 0, are limitele iterate n origine egale cu zero, nsa nu are
limita n origine.
R:

In adevar,
lim
y0
_
lim
x0
f (x, y)
_
= 0, lim
x0
_
lim
y0
f (x, y)
_
= 0.
Insa pe parabola x
2
= my, avem
lim
(x,y)(0,0)
f (x, y) = lim
y0
my
2
(m
2
+ 1) y
2
=
m
1 +m
2
.
Pentru diferite valori ale lui m se obt in valori diferite ale limitei, deci f nu are limita n
origine.
3.21 Sa se cerceteze existent a limitelor iterate si a limitei n origine pentru urmatoarele
funct ii:
1) f (x, y) =
xy
x
2
+y
2
. 2) f (x, y) = xsin
1
y
+y cos
1
x
.
3) f (x, y) =
2x 3y +x
2
+y
2
x +y
. 4) f (x, y) =
2xy
2
2x
2
+ 5y
4
.
5) f (x, y) =
y
2
2x
y
2
+ 2x
. 6) f (x, y) =
x y + 2x
2
+y
2
x +y
. 7) f (x, y) = xcos
1
y
.
8) f (x, y) = (x +y) sin
1
x
sin
1
y
, 9) f (x, y) =
sin
_
x
3
+y
3
_
x
2
+y
2
,
10) f (x, y) =
(x +y) tg
_
x
2
+y
2
_
_
x
2
+y
2
. 11) f (x, y, z) =
xyz
x
3
+y
3
+z
3
.
12) f (x, y) =
x
2
+y
2
_
x
2
+y
2
+ 1 1
. 13) f (x, y) =
_
1 +x
2
y
2
_
1
x
2
+y
2
.
14) f (x, y) =
1 cos
_
x
2
+y
2
_
x
2
y
2
(x
2
+y
2
)
.
R: 1) Exista limitele iterate si sunt egale cu 0, dar nu exista limta n origine. 2) Nu
exista limitele iterate, deoarece sin
1
y
nu are limita pentru y 0 si cos
1
x
nu are limita
pentru x 0. Funct ia are nsa limita n origine, deoarece
0 [f (x, y)[ [x[
sin
1
y
+[y[
cos
1
x
[x[ +[y[ 0.
3) Exista limitele iterate:
lim
y0
_
lim
x0
f (x, y)
_
= 3, lim
x0
_
lim
y0
f (x, y)
_
= 2.
Daca limitele iterate exista, sunt nite si distincte nu exista limita n punct. 8) Se t ine
seama ca
[x +y[ [f (x, y)[ [x +y[ .
9) Funct ia se mai scrie
f (x, y) =
sin
_
x
3
+y
3
_
x
3
+y
3

x
3
+y
3
x
2
+y
2
,
iar

x
3
+y
3
x
2
+y
2
[x[
3
+[y[
3
x
2
+y
2
< 2 ([x[ +[y[) .
lim
(x,y)(1,0)
ln (x +e
y
)
_
(x 1)
2
+y
2
.
R: Fie (x, y) n interiorul discului cu centrul n punctul (1, 0) si de raza r. Obt inem
x = 1 +r cos , y = r sin , [0, 2). Deci
lim
(x,y)(1,0)
ln (x +e
y
)
_
(x 1)
2
+y
2
= lim
r0
ln
_
1 +r cos +e
r sin
_
r
= .
1) lim
(x,y)(0,0)
xy
xy + 1 1
. 2) lim
(x,y)(0,2)
sin xy
x
.
R: 1) Suntem n cazul de except ie
0
0
. Rat ionalizam numitorul. Avem
lim
(x,y)(0,0)
xy
xy + 1 1
= lim
(x,y)(0,0)
_
_
xy + 1 + 1
_
= 2.
2) Avem
lim
(x,y)(0,2)
sin xy
x
= lim
(x,y)(0,2)
sin xy
xy
y = 2.
1) lim
(x,y)(0,0)
_
x
2
+y
2
_
sin
1
xy
. 2) lim
(x,y)(0,0)
x
x +y
.
3) lim
(x,y)(,k)
_
1 +
y
x
_
x
. 4) lim
(x,y)(,)
x +y
x
2
+y
2
.
R: 1) Deoarece
_
x
2
+y
2
_
sin
1
xy
x
2
+ y
2
, limita este 0. 2) Funct ia nu are limita.
De exemplu, pe dreapta y = mx se obt ine o limita ce depinde de m. 3) Limita este e
k
.
4) Putem presupune x +y > 1. Limita este 0.
Capitolul 4
Funct ii continue
4.1 Continuitatea funct iilor reale de o variabila reala
4.1 Sa se determine real a.. urmatoarele funct ii sa e continue pe mult imile lor de
denit ie:
1) f : [1, 3] R, denita prin
f(x) =
_
2
2x +x
2
, x [1, 2),
x + 3, x [2, 3].
2) f : [0, 2] R, denita prin
f(x) =
_
6 sin (x1)
x1
, x [0, 1),
+ 5x, x [1, 2].
R: 1) =
1
3
. 2) = 1.
4.2 Sa se determine real a.. urmatoarele funct ii sa e continue n punctele indicate:
1) f : R R, denita prin
f(x) =
_
(1cos x)
x
2
, x ,= 0,
2
2
, x = 0,
, x
0
= 0.
2) f : [1, ) R, denita prin
f(x) =
_
arctg (x1)
x
2
1
, x ,= 1,
2
, x = 1,
, x
0
= 1.
f(x) =
_
(1 +x)
1
x
, x > 0,
x +e, x 0,
, x
0
= 0.
50
CAPITOLUL 4. FUNCT II CONTINUE 51
f(x) =
_
2
x+2
16
4
x
16
, x ,= 2,
, x = 2,
, x
0
= 2.
5) f : [0, ] R, denita prin
f(x) =
_
e
3x
, x [0, 1],
sin(x1)
x
2
5x+4
, x (1, ],
, x
0
= 1.
f(x) =
_
_
(x +e
x
)
1
x
, x < 0,
e
2
, x = 0,
(sin x + cos x)
x
, x > 0,
, x
0
= 0.
R: 1) 0, 1. 2)
_
0,
1
2
_
. 3) = 1. 4) =
1
2
. 5) = 3e
3
. 6) = 2.
4.3 Sa se determine punctele de discontinuitate ale funct iilor:
1) f(x) =
_
x
x, x > 0. 2) f(x) = x
_
1
x
_
, x ,= 0, f(0) = 1.
3) f(x) = xsin
1
x
, x ,= 0, f(0) = 0. 4) f(x) = x
p
arctg
1
x
, x ,= 0, f(0) = 0, p > 0.
R: 1) Discontinua n x = n
2
, n N. 2) Discontinua n x =
1
k
, cu k ntreg nenul. 3)
si 4) Funct ii continue pe R.
4.4 Sa se studieze continuitatea funct iei f : R R denita prin:
f(x) =
_
x
3
x
2
, x Q,
1
4
x, x R Q.
R: Daca x
0
R este un punct de continuitate pentru f, atunci pentru orice sir
x
n
Q, x
n
x
0
si orice sir x
n
R Q, x
n
x
0
, avem: x
3
0
x
2
0
=
1
4
x
0
, de unde
rezulta ca x
0

_
0,
1
2
_
.
4.5 Fie funct ia f : [0, 1] R, denita prin
f(x) =
_
x, x Q,
1 x, x R Q.
Sa se studieze continuitatea, sa se arate ca f ([0, 1]) este un interval si ca f nu are
proprietatea lui Darboux.
R: Punctul x
0
[0, 1] este un punct de continuitate pentru f d.d.

x
0
= 1 x
0
,
adica x
0
=
1
5
2
este singurul punct de continuitate al lui f. Pentru orice x [0, 1],
x, 1x [0, 1], deci f ([0, 1]) [0, 1]. Fie y [0, 1]. Daca y Q, exista x = y
2
(x Q)
a.. f(x) = y, iar daca y R Q, exista x = 1 y (x R Q) a.. f(x) = y. Asadar,
[0, 1] f ([0, 1]). Avem: f ([0, 1]) = [0, 1]. Pentru a arata ca f nu are proprietatea lui
Darboux, e intervalul
_
1
9
,
1
4
[0, 1], cu f
_
1
9
_
=
1
3
, f
_
1
4
_
=
1
2
. Consideram =
1
4
17

_
1
3
,
1
2
_
si aratam ca ecuat ia f(x) = nu are solut ii n intervalul
_
1
9
,
1
4
_
. Daca x Q,
x =
1
4
17
, da x =
1
17
/ Q, daca x R Q, 1 x =
1
4
17
, da x = 1
1
4
17
/
_
1
9
,
1
4
_
,
deoarece 1
1
4
17
>
1
4
.
4.2 Continuitatea uniforma a funct iilor de o variabila
4.6 Sa se arate ca funct ia f(x) = x
3
, x [1, 3] este uniform continua pe [1, 3].
R:

Intr-adevar,
[f(x) f(x
)[ = [x x
[ (x
2
+xx
+x
2
) < 27 [x x
[ < ,
pentru orice x, x
[1, 3] pentru care [x x
[ < (), cu () =

27
.
4.7 Sa se arate ca funct ia f : (0, ) R, denita prin
f(x) =
x
x + 1
+x,
este uniform continua pe (0, ).
R: Fie x, x
(0, ). Avem
[f(x) f (x
)[ = [x x
[
_
1 +
1
(1 +x) (1 +x
)
_
< 2 [x x
[ < ,
daca [x x
[ < () =

2
.
4.8 Sa se arate ca funct ia f : (1, ) R, denita prin
f(x) =
x
x + 1
+x,
nu este uniform continua pe (1, ).
R:

Intr-adevar, sa consideram sirurile x
n
=
n+1
n+2
, x
n
=
n
n+1
. Avem
[x
n
x
n
[ =
1
(n + 1) (n + 2)
.
Punctele x
n
si x
n
sunt oricat de apropiate pentru n sucient de mare, nsa
[f (x
n
) f (x
n
)[ = 1 +
1
(n + 1) (n + 2)
> 1,
deci funct ia nu este uniform continua.
4.9 Sa se arate ca funct ia f : [a, e] R, a > 0, denita prin f (x) = ln x, este uniform
continu a pe [a, e].
R: Funct ia f este continua pe intervalul [a, e] marginit si nchis, deci este uniform
continua pe acest interval.
4.10 Sa se arate ca funct ia f : (0, 1) R, denita prin f (x) = ln x, este nu uniform
continu a pe (0, 1).
R: Fie x
n
=
1
n
, x
n
=
1
n
2
+1
. Avem [x
n
x
n
[ < , dar
[f (x
n
) f (x
n
)[ =
ln
n
2
+ 1
n
.
4.11 Sa se studieze uniforma continuitate a funct iei f : R R, denita prin f (x) =
xsin
2
x
2
.
R: Fie
x
n
=
_
(4n + 1)

2
, x
n
=
_
(4n + 3)

2
.
Avem
[x
n
x
n
[ =

_
(4n + 1)

2
+
_
(4n + 3)

2
0
si
[f (x
n
) f (x
n
)[ =
_
(4n + 1)

2

_
(4n + 3)

2
0.
Dar, pentru x
n
=
2n, avem
[f (x
n
) f (x
n
)[ =
_
(4n + 1)

2

2n 0
.
Asadar, f nu este uniform continua pe R.
4.12 Sa se studieze uniforma continuitate a urmatoarelor funct ii:
1) f : (0, 1) R, f(x) = ln x. 2) f : [a, e] R, f (x) = ln x, a > 0.
3) f :
_
0,
1
_
R, f (x) = sin
1
x
. 4) f : R [1, 1] , f (x) = sin x
2
.
5) f : [0, 1] R, f (x) =
1
x
2
x 2
. 6) f : R [1, 1] , f (x) = cos x.
7) f : (0, 1) R
+
, f (x) =
1
x
. 8) f : [0, ) R, f (x) = x
2
.
R: 1) Nu. 2) Da. 3) Nu. 4) Nu. 5) Da. 6) Da, se t ine seama ca
[cos x cos x
[ 2
sin
x x
2 [x x
[ .
7) Nu, este sucient sa luam x
n
=
1
n
si x
n
=
1
n+1
. 8) Nu, este sucient sa luam x
n
= n
si x
n
= n +
1
n
.
4.3 Continuitatea funct iilor de o variabila vectoriala
f (x, y) =
_
x
2
y
3
x
2
+y
2
, x
2
+y
2
,= 0,
0, x
2
+y
2
= 0,
este continua pe R
2
.
R: Funct ia este continua n orice punct n care x
2
+ y
2
,= 0, adica n orice punct cu
except ia originii. Ramane de vericat numai continuitatea n origine, ceea ce revine la a
arata ca funct ia are limita n origine si aceasta este egala cu 0. Avem, nsa:
x
2
y
3
x
2
+y
2
<
[x[ [y[
x
2
+y
2
[x[ y
2
1
2
[x[ y
2
,
deoarece x
2
+y
2
2 [x[ [y[. Deci limita funct iei este 0.
f (x, y) =
_
sin(x
3
+y
3
)
x
2
+y
2
, x
2
+y
2
,= 0,
0, x
2
+y
2
= 0,
este continua pe R
2
.
R: Funct ia este continua n orice punct n care x
2
+ y
2
,= 0, adica n orice punct cu
except ia originii. Ramane de vericat numai continuitatea n origine, ceea ce revine la a
arata ca funct ia are limita n origine si aceasta este egala cu 0. Putem scrie:
sin
_
x
3
+y
3
_
x
2
+y
2
=
sin
_
x
3
+y
3
_
x
3
+y
3

x
3
+y
3
x
2
+y
2
.
Insa, pentru (x, y) (0, 0) avem lim

sin(x
3
+y
3
)
x
3
+y
3
= 1 si
x
3
+y
3
x
2
+y
2
[x[
3
+[y[
3
x
2
+y
2
< [x[ +[y[ .
4.15 Sa se cerceteze continuitatea funct iei
f (x, y) =
_ _
1 x
2
y
2
, x
2
+y
2
1,
0, x
2
+y
2
> 1.
R: Punem r =
_
x
2
+y
2
. Funct ia este continua pe R
2
.
f (x, y) =
_
2xy
x
2
+y
2
, x
2
+y
2
,= 0,
0, x
2
+y
2
= 0,
este continua part ial n raport cu x si y, dar nu este continua n origine.
R: Fie (x
0
, y
0
) R
2
. Funct iile f (x, y
0
) si f (x
0
, y) sunt continue n orice punct.
Funct ia f (x, y) nu are limita n origine.
4.17 Sa se cerceteze continuitatea urmatoarelor funct ii:
1) f (x, y) =
_
1cos(x
3
+y
3
)
x
2
+y
2
, x
2
+y
2
,= 0,
0, x
2
+y
2
= 0.
2) f (x, y) =
_
(1 +xy)
1
x+
y
, x > 0, y > 0,
1, x = 0 sau y = 0.
R: 1) Se t ine seama ca 1 cos
_
x
3
+y
3
_
= 2 sin
2 x
3
+y
3
2
. Funct ia este continua. 2)
Putem scrie
(1 +xy)
1
x+
y
=
_
(1 +xy)
1
xy
_
xy
x+
y
si
xy
x+
xy
_
x +
y
_
. Funct ia este continua.
4.18 Sa se discute dupa valorile parametrului continuitatea urmatoarelor funct ii:
1) f (x, y) =
_
1cos
x
2
+y
2
tg (x
2
+y
2
)
, 0 < x
2
+y
2
<

2
,
, (x, y) = (0, 0) .
2) f (x, y, z) =
_
x
2
y
2
z
2
x
6
+y
6
+z
6
, (x, y, z) ,= (0, 0, 0) ,
, (x, y, z) = (0, 0, 0) .
3) f (x, y, z) =
_
3x+2yz+x
2
+yz
x+y+z
, (x, y, z) ,= (0, 0, 0) ,
, (x, y, z) = (0, 0, 0) .
4) f (x, y, z) =
_
_
_
(x+y+z)tg (x
2
+y
2
+z
2
)
x
2
+y
2
+z
2
, (x, y, z) ,= (0, 0, 0) ,
, (x, y, z) = (0, 0, 0) .
R: 1) Notam r =
_
x
2
+y
2
. Pentru r 0 avem lim
1cos
r
tg r
=
1
2
. Funct ia este
continua pe
_
0,

2
_
pentru =
1
2
.
2) Fie x = t, y = mt, z = nt, t R o dreapta prin origine. Deoarece
lim
t0
f (t, mt, nt) =

2
m
2
n
2
6
+m
6
+n
6
,
deci depinde de direct ie, rezulta ca f nu are limita n origine. Funct ia este continua pe
R
3
(0, 0, 0).
Capitolul 5
Derivate si diferent iale
5.1 Derivata si diferent iala funct iilor de o variabila
5.1 Utilizand denit ia, sa se calculeze derivatele urmatoarelor funct ii, n punctele spe-
cicate:
1) f (x) =
x + 2, x
0
= 7. 2) f (x) = ln
_
x
2
+ 5x
_
, x
0
= 1.
3) f (x) = sin 3x
2
, x
0
=
. 4) f (x) = arcsin (x 1) , x
0
= 1.
5) f (x) = e
3x
, x
0
= 1. 6) f (x) = tg x, x
0
=

4
.
5.2 Sa se studieze derivabilitatea urmatoarelor funct ii, n punctele specicate:
1) f :
_
1
2
,
_
R, f (x) =
_
ln (1 + 2x) , x (
1
2
, 0],
2x, x (0, ) ,
x
0
= 0.
2) f : (0, ) R, f (x) =
_
x
2
+ 5x + 2, x (0, 2],
9
8
x +
7
4
, x (0, ) ,
x
0
= 2.
R: 1) f
(0) = 2. 2) f
(2) =
9
8
.
5.3 Sa se calculeze derivatele urmatoarelor funct ii:
1) f (x) = x
4
+ 5x
3
8. 2) f (x) = x
2
+
x
3
x.
3) f (x) = xcos x. 4) f (x) =
x1
x
2
+1
.
5) f (x) =
sin x
2+cos x
. 6) f (x) = ln
x
2
x+1
.
7) f (x) =
3
_
1x
2
1+x
2
. 8) f (x) = e
x
2
cos x
.
R: Se obt ine:
1) f
(x) = 4x
3
+ 15x
2
. 2) f
(x) = 2x +
1
2
x

1
3(
3
x)
2
.
3) f
(x) = cos x xsin x. 4) f
(x) =
x
2
2x1
(x
2
+1)
2
.
5) f
(x) =
2 cos x+1
(2+cos x)
2
. 6) f
(x) =
1
x
x+2
x+1
.
7) f
(x) =
4
3
x
(1+x
2
)
2
3
_
_
1+x
2
1x
2
_
2
.
8) f
(x) =
_
2xcos x x
2
sin x
_
e
x
2
cos x
.
56
CAPITOLUL 5. DERIVATE SI DIFERENT IALE 57
1) f (x) = ln
_
2 sin x + 1 +
2 sin x 1
_
. 2) f (x) =
sin x
cos
2
x
+ ln
1+sin x
cos x
.
3) f (x) =
x
2
x
2
+k +
k
2
ln
_
x +
x
2
+k
_
. 4) f (x) = 5 sh
3 x
15
+ 3 sh
5 x
15
.
5) f (x) = e
x
arctg e
x
ln
1 +e
2x
. 6) f (x) =
x
x
e
x
(xln x x 1) .
7) f (x) =
x
2
a
2
x
2
+
a
2
2
arcsin
x
a
. 8) f (x) = log
e
2
_
x
n
+
x
2n
+ 1
_
.
R: Se obt ine:
1) f
(x) =
cos x
(4 sin
2
x1)
. 2) f
(x) =
2
cos
3
x
.
3) f
(x) =
x
2
+k. 4) f
(x) = sh
2 x
15
ch
3 x
15
.
5) f
(x) = e
x
arctg e
x
. 6) f
(x) = x
x+1
e
x
(ln x) (ln x 1).
7) f
(x) =
a
2
x
2
. 8) f
(x) =
nx
n1
2
x
2n
+1
.
1) f (x) = ln
1+
sin x
1
sin x
+ 2 arctg
_
sin x
_
.
2) f (x) =
3
4
ln
x
2
+1
x
2
1
+
1
4
ln
x1
x+1
+
1
2
arctg x.
3) f (x) =
1
3
ln (1 +x)
1
6
ln
_
x
2
x + 1
_
+
1
3
arctg
2x1
3
.
4) f (x) = 3b
2
arctg
_
x
bx
(3b + 2x)
bx x
2
.
R: 1) f
(x) =
2
cos x
sin x
. 2) f
(x) =
x(x3)
x
4
1
. 3) f
(x) =
1
x
3
+1
.
4) f
(x) = 4x
_
x
bx
.
1) f (x) =
arcsin x
x
+ ln
x
1+
1x
2
.
2) f (x) = ln
x
4
+x
2
+ 1 +
2
3
arctg
2x
2
+1
3
.
3) f (x) =
x
4(x
2
+1)
2
+
3x
8(x
2
+1)
+
3
8
arctg x.
4) f (x) =
5
2
_
(2x
2
+ 8x + 1)
13
2
ln
_
2 (x + 2) +
_
(2x
2
+ 8x + 1)
_
.
R: Se obt ine:
1) f
(x) =
arcsin x
x
2
. 2) f
(x) =
2x
3
+3x
x
4
+x
2
+1
.
3) f
(x) =
1
(x
2
+1)
3
. 4) f
(x) =
5x3
2x
2
+8x+1
.
5.7 Sa se arate ca derivata unei funct ii pare este o funct ie impara, iar derivata unei
funct ii impare este o funct ie para.
5.8 Sa se arate ca derivata unei funct ii periodice este o funct ie periodic a.
5.9 Sa se arate ca funct ia y = xe
x
satisface relat ia xy
= (1 x) y.
5.10 Sa se arate ca funct ia y = xe
x
2
2
=
_
1 x
2
_
y.
5.11 Sa se arate ca funct ia y =
1
1+x+ln x
= y (y ln x 1).
5.12 Sa se calculeze derivatele de ordinul doi ale urmatoarelor funct ii:
1) f (x) = x
8
+ 7x
6
5x + 4. 2) f (x) = (arcsin x)
2
. 3) f (x) = e
x
2
.
4) f (x) = ln
_
x +
a
2
+x
2
_
. 5) f (x) =
_
1 +x
2
_
arctg x. 6) f (x) = sin
2
x.
R: Se obt ine:
1) f
(x) = 56x
6
+ 210x
4
. 2) f
(x) =
2
1x
2
+
2x
(1x
2
)
3
arcsin x.
3) f
(x) = 2e
x
2
+ 4x
2
e
x
2
. 4) f
(x) =
x
(a
2
+x
2
)
3
.
5) f
(x) = 2 arctg x + 2
x
x
2
+1
. 6) f
(x) = 2 cos 2x.

5.13 Sa se calculeze derivatele de ordinul n ale urmatoarelor funct ii:
1) f (x) = e
ax
. 2) f (x) =
1
xa
. 3) f (x) =
1
x
2
a
2
.
4) f (x) = cos x. 5) f (x) = sin x. 6) f (x) = ln
2x
x
2
1
.
7) f (x) = 2
x
. 8) f (x) =
1
x
2
3x+2
. 9) f (x) = ln (ax +b) .
10) f (x) = e
ax
e
bx
. 11) f (x) =
1
ax+b
. 12) f (x) = (1 +x)
.
R: 3) Se t ine seama de identitatea:
1
x
2
a
2
=
1
2a
_
1
xa

1
x+a
_
.
4) f
(n)
(x) = cos
_
x +
n
2
_
. 5) f
(n)
(x) = sin
_
x +
n
2
_
.
6). f
(x) =
x
2
+1
x(x
2
+1)
si se scrie fract ia ca suma de fract ii simple.
7) f
(n)
(x) = 2
x
ln
n
2.
8) f (x) =
1
x2

1
x1
, se obt ine f
(n)
(x) = (1)
n
n!
_
1
(x2)
n+1

1
(x1)
n+1
_
.
9) f
(n)
(x) = (1)
n1 (n1)!a
n
(ax+b)
n . 10) f
(n)
(x) = e
ax
e
bx
(a +b)
n
.
11) f
(n)
(x) = (1)
n
n!a
n
(ax+b)
n+1
.
12) Avem: f
(n)
(x) = ( 1) ( n + 1) (1 +x)
n
.
5.14 Fie f (x) = x
2
e
3x
. Sa se calculeze f
(10)
(x).
R: Se aplica formula lui Leibniz. Se obt ine: f
(10)
(x) = 3
9
e
3x
_
3x
2
+ 20x + 30
_
.
5.15 Fie f (x) = x
2
sin x. Sa se calculeze f
(20)
(x).
R: Se aplica regula lui Leibniz. Se obt ine: f
(20)
(x) = x
2
sinx 40xcos x 380 sin x.
5.16 Utilizand regula lui Leibniz, sa se calculeze derivatele de ordinul n ale funct iilor:
1) f (x) = x e
x
. 2) f (x) = x
2
e
2x
. 3) f (x) =
_
1 x
2
_
cos x.
4) f (x) =
1+x
x
. 5) f (x) = x
3
ln x.
5.17 Se considera funct ia polinomiala f (x) = x
4
+ x
3
+ x
2
+ x + 1. Sa se calculeze
suma: S =
4
k=1
1
x
k
2
, unde x
k
sunt radacinile ecuat iei f (x) = 0.
R: Din f (x) = (x x
1
) (x x
2
) (x x
3
) (x x
4
), prin derivare, deducem:
f
(x)
f (x)
=
4
k=1
1
x x
k
.
Deci S =
f
(2)
f(2)
=
49
31
.
5.18 Sa se determine cu cat se modica (aproximativ) latura unui patrat daca aria sa
creste de la 9 m
2
la 9, 1 m
2
.
R: Daca x este aria patratului si y latura sa, atunci y =
x. Se dau: x
0
= 9, h = 0, 1.
Cresterea laturii patratului este data de:
y y
0
dy = f
(x) h =
1
2
9
0, 1 = 0, 016 m.
5.19 Sa se gaseasca cresterea yy
0
si diferent iala dy ale funct iei y = 5x+x
2
n punctul
x
0
= 2, daca h = 0, 001.
R: y y
0
= 0, 009001 si dy = 0, 009.
5.20 Sa se calculeze diferent iala funct iei y = cos x n punctul x
0
=

6
, pentru h =

36
.
5.21 Sa se calculeze diferent iala funct iei y =
2
x
n punctul x
0
= 9, pentru h = 0, 01.
5.22 Sa se calculeze diferent ialele funct iilor:
1) f (x) =
1
x
n
. 2) f (x) = xln x x. 3) f (x) =
x
1x
.
4) f (x) = ln
1x
1+x
. 5) f (x) = x
2
e
x
. 6) f (x) = e
x
sin x.
R: Se obt ine:
1) df (x) =
n
x
n+1
dx. 2) df (x) = ln xdx. 3) df (x) =
1
(1x)
2
dx.
4) df (x) =
2
x
2
1
dx. 5) df (x) = x(2 x) e
x
dx. 6) df (x) = e
x
(sin x + cos x) dx.
5.23 Sa se calculeze diferent ialele de ordinul doi ale funct iilor:
1) f (x) =
1 x
2
. 2) f (x) = arccos x. 3) f (x) = sin xln x.
4) f (x) =
1
x
ln x. 5) f (x) = x
2
e
x
. 6) f (x) = e
x
sin x.
d
n
(arctg x) = (1)
n1
(n 1)!
(1 +x
2
)
n/2
sin
_
narctg
1
x
_
dx
n
.
5.2 Proprietat i ale funct iilor derivabile
5.25 Sa se determine abscisele punctelor de extrem ale funct iilor:
1) f (x) = 2 cos x +x
2
. 2) f (x) = x
2
(x 12)
2
. 3) f (x) =
x
2
2x+2
x1
.
4) f (x) =
3
_
(x
2
1)
2
. 5) f (x) = 2 sin 2x + sin 4x. 6) f (x) = 2 cos
x
2
+ 3 cos
x
3
.
R: 1) x
0
= 0 este punct de minim.
2) x
1
= 0, x
2
= 12 sunt puncte de minim, x
3
= 6 este punct de maxim.
3) x
1
= 0 este punct de maxim, x
2
= 2 este punct de minim.
4) x
1,2
= 1 sunt puncte de minim, x
3
= 0 este punct de maxim.
5) x
k
=
6
+k sunt puncte de minim, x
k
=

6
+k sunt puncte de maxim, k Z.
6) x
k
= 12k si x
k
= 12
_
k
2
5
_
sunt puncte de maxim, y
k
= 6 (2k + 1) si
y
k
= 12
_
k
1
5
_
sunt puncte de minim, k Z.
5.26 Fie a
1
, a
2
, . . . , a
n
(0, ) si a
x
1
+ a
x
2
+ + a
x
n
n pentru orice x R. Sa se
arate ca atunci a
1
a
2
a
n
= 1.
R: Fie funct ia f : R R, denita prin f (x) = a
x
1
+ a
x
2
+ + a
x
n
. Avem ca
f (x) n = f (0), x R, deci x
0
= 0 este un punct de minim pentru f si conform
teoremei lui Fermat: f
(0) = 0.
5.27 Fie a, b (0, ) 1 a.. a
x
2
b +b
x
2
a 2ab, pentru orice x R. Sa se arate
ca ab = 1.
R: Fie unct ia f : R R, denita prin f (x) = a
x
2
b + b
x
2
a. Avem ca f (x)
2ab = f (1), x R, deci x
0
= 1 este un punct de minim pentru f si conform teoremei
lui Fermat: f
(1) = 0.
5.28 Sa se studieze aplicabilitatea teoremei lui Rolle pentru funct ia f :
_
0,

2
R,
denita prin
f (x) =
_
cos x, x
_
0,

4
,
sinx, x
_
4
,

2
.
R: Funct ia nu este derivabila n

4
.
5.29 Sa se studieze aplicabilitatea teoremei lui Rolle pentru funct iile f : [0, 2] R,
denite prin:
1) f (x) = [x 1[ . 2) f (x) = [x 1[
3
.
R: 1) Nu. 2) Da, c = 1.
5.30 Sa se studieze aplicabilitatea teoremei lui Rolle pentru funct iile f :
_
2
,

2
R,
denite prin:
1) f (x) = [sin x[ . 2) f (x) =
sin
3
x
.
R: 1) Nu. 2) Da, c = 0.
5.31 Sa se arate ca polinomul lui Legendre P
n
(x) =
d
n
dx
n
_
x
2
1
_
n
are n radacini dis-
tincte n intervalul (1, 1).
R: Se aplica de n ori teorema lui Rolle funct iei f (x) =
_
x
2
1
_
n
.
5.32 Fie f : [a, b] R o funct ie continua pe [a, b], derivabila pe (a, b) si a.. f (a) =
f (b). Sa se arate ca exista c (a, b) a.. f (a) f (c) = f
(c) (c a).
R: Se aplica teorema lui Rolle funct iei g (x) = (x a) f (x) xf (a) pe intervalul
[a, b].
5.33 Fie numerele reale a
0
, a
1
, a
2
, . . . , a
n
care verica relat ia
a
0
1
+
2a
1
2
+
2
2
a
2
3
+ +
2
n
a
n
n + 1
= 0.
Sa se arate ca funct ia f :
_
1, e
2
R, denita prin f (x) = a

0
+a
1
ln x+a
2
ln
2
x+ +
a
n
ln
n
x se anuleaza cel put in ntr-un punct din intervalul
_
1, e
2
_
.
R: Se aplica teorema lui Rolle funct iei g (x) = a
0
lnx +
a
1
ln
2
x
2
+ +
a
n
ln
n+1
x
n+1
.
5.34 Fie f : [a, b] R o funct ie continua pe [a, b], derivabila pe (a, b). Sa sea arate ca
exista c (a, b) a.
f
(c) =
a +b 2c
(c a) (c b)
.
R: Se aplica teorema lui Rolle funct iei g (x) = e
f(x)
(x a) (x b) pe intervalul [a, b].
5.35 Se considera funct ia f : [1, 1] R, denita prin:
f (x) =
_
x
2
+mx +n, x [1, 0] ,
px
2
+ 4x + 4, x (0, 1].
Sa se determine m, n, p R a.. f sa satisfaca ipotezele teoremei lui Rolle pe intervalul
[1, 1] si sa se gaseasca valoarea constantei c n acest caz.
R: n = 4, m = 4, p = 7, c =
2
7
.
5.36 Fie f, g : [a, b] R doua funct ii continue pe [a, b], derivabile pe (a, b) si cu
f (a) = f (b). Sa se arate ca ecuat ia f (x) g
(x) + f
(x) = 0 are cel put in o solut ie n

intervalul (a, b).
R: Fie h : [a, b] R, denita prin h(x) = f (x) e
g(x)
, care este o funct ie Rolle. Exista
deci c (a, b) a.. h
(c) = 0. Dar h
(x) = f
(x) e
g(x)
+f (x) g
(x) e
g(x)
.
5.37 Fie f : [a, b] R o funct ie de trei ori derivabila pe [a, b] a.. f (a) = f (b) = 0 si
f
(a) = f
(b) = 0. Sa se arate ca exista cel put in un punct c (a, b) a.. f
(c) = 0.
R: Aplicam teorema lui Rolle. Exista d (a, b) a.. f
(d) = 0. Exista apoi c

1
(a, d)
si c
2
(d, b) a.. f
(c
1
) = 0 si

f
(c
2
) = 0. Deci exista c (c
1
, c
2
) a.. f
(c) = 0.
5.38 Sa se cerceteze aplicabilitatea teoremei lui Lagrange pentru funct ia f : [0, 1] R,
denita prin f (x) =

x
2
+ax, a > 0, si n caz armativ sa se determine constanta c
corespunzatoare.
R: Da, c =
1
2
_
a +
a
2
+a
_
(0, 1).
5.39 Sa se cerceteze aplicabilitatea teoremei lui Lagrange pentru funct iilor f, denite
prin:
1) f (x) =
_
x, x [1, 2] ,
x
2
4
+ 1, x (2, 3].
2) f (x) =
_
x
2
, x [0, 1] ,
2x 1, x (1, 2].
3) f (x) =
_
x + 1, x (0, 3],
x
2
+ 1, x [4, 0] .
4) f (x) =
_
3x
2
2
, x [0, 1] ,
1
x
, x (1, 2].
R: 1) Da, f
(c) =
9
8
, c =
9
4
. 2) Da, c =
3
4
. 3) Da, c =
13
36
. 4) Da, c
1
=
1
2
, c
2
=
2.
5.40 Sa se determine abscisa c a unui punct n care tangenta la gracul funct iei f :
R R, denita prin
f (x) =
_
x+2
2
, x 0,
x + 1, x > 0,
este paralela cu coarda care uneste punctele de pe grac de abscise x
1
= 4 si x
2
= 3.
R: c =
13
36
.
5.41 Sa se arate ca
3
30 3 <
1
9
.
R: Se aplica teorema lui Lagrange funct iei f : [27, 30] R, denita prin f (x) =
3
x.
5.42 Sa se gaseasca solut iile reale ale ecuat iei (a 1)
x
+ (a + 3)
x
= a
x
+ (a + 2)
x
, cu
a > 1.
R: Ecuat ia se mai scrie: a
x
(a 1)
x
= (a + 3)
x
(a + 2)
x
. Consideram funct ia f :
(0, ) R, denita prin f (t) = t
x
, pentru x R, xat. Aplicam teorema lui Lagrange
pe intervalele [a 1, a] si [a + 2, a + 3]. Exista deci c
1
(a 1, a) si c
2
(a + 2, a + 3)
a.. f (a) f (a 1) = f
(c
1
) si f (a + 3) f (a + 2) = f
(c
2
). Din f
(c
1
) = f
(c
2
) cu
c
1
,= c
2
, rezulta x
1
= 0, x
2
= 1.
5.43 Fie f o funct ie de doua ori derivabila ntr-o vecinatate V a punctului a R. Sa
se arate ca pentru orice h sucient de mic exista punctele p, q V a..
f (a +h) f (a h)
2h
= f
(p) ,
f (a +h) 2f (a) +f (a h)
h
2
= f
(q) .
5.44 Sa se cerceteze aplicabilitatea teoremei lui Cauchy pentru funct iile f si g, denite
prin:
1) f, g : [1, e] R, f (x) = ln x, g (x) =
e
x
.
2) f, g : [2, 5] R, f (x) =
_
x + 3, x [2, 1),
x
4
+
7
4
, x [1, 5] ,
g (x) = x.
3) f, g : [0, 3] R, f (x) =
_
x
3
3
x
2
+ 1, x [1, 3] ,
x +
4
3
, x [0, 1] ,
g (x) = x.
R: 1) Da, c =
e
e1
. 2) Da, c =
1
16
. 3) Da, c =
2
2
3
+ 1.
5.45 Sa se calculeze, utilizand regula lui l
Hospital:
1) lim
x0
tg xx
xsin x
. 2) lim
x1
x
x
x
ln xx+1
. 3) lim
x0
ln(sin 2x)
ln(sin 3x)
.
4) lim
x
x
n
e
ax
, a > 0. 5) lim
x0
_
ctg x
1
x
_
. 6) lim
x0
_
(1+x)
1
x
e
_1
x
.
7) lim
x0
_
1
x
2
ctg
2
x
_
. 8) lim
x
_
x x
2
ln
1+x
x
_
. 9) lim
x1
_
tg
x
4
_
tg
x
2
.
R: 1) 2. 2) 2. 3) 1. 4) 0. 5) 0. 6)
1
2
. 7) Putem scrie:
1
x
2
ctg
2
x =
sin
2
x x
2
cos
2
x
x
2
sin
2
x
si se aplica de patru ori regula lui l
Hospital. Se obt ine

2
3
. 8) Luam x =
1
t
, cu t 0
pentru x . Se obt ine
1
2
. 9)
1
e
.
5.46 Sa se calculeze, utilizand regula lui l
Hospital:
1) lim
x0
tg x xsin x
x sin x
. 2) lim
x
x[ln x ln (x + 1)] + 1
ex[ln (ex + 1) ln x] 1
.
R: 1) 5. 2) e.
5.47 Sa se dezvolte polinomul f (x) = x
3
2x
2
+3x +5 dupa puterile binomului x 2.
R: f (x) = 11 + 7 (x 2) + 4 (x 2)
2
+ (x 2)
3
.
5.48 Sa se determine o funct ie polinomiala de gradul trei a.. f (0) = 1, f
(0) = 1,
f
(0) = 2 si f
(0) = 6.
R: Polinomul Taylor al funct iei f este f (x) = 1 +x +x
2
+x
3
.
5.49 Sa se gaseasca primii 5 termeni din dezvoltarea Taylor a funct iei f (x) = e
x
dupa
puterile binomului x + 1.
R: P
4
(x) =
1
e
+
1
e
(x + 1) +
1
2e
(x + 1)
2
+
1
6e
(x + 1)
3
+
1
24e
(x + 1)
4
.
5.50 Sa se gaseasca primii 5 termeni din dezvoltarea Taylor a funct iei f (x) = ln x dupa
puterile binomului x 1.
R: P
4
(x) = (x 1)
1
2
(x 1)
2
+
1
3
(x 1)
3
1
4
(x 1)
4
.
5.51 Sa se evalueze eroarea comisa n aproximarea:
e 2 +
1
2!
+
1
3!
+
1
4!
.
R: Avem ca: e
x
= 1 +
1
1!
x +
1
2!
x
2
+
1
3!
x
3
+
1
4!
x
4
+ R
4
(x), unde R
4
(x) =
x
5
5!
e
x
, cu
(0, 1). Pentru x = 1, [R
4
(1)[
3
5!
=
1
40
.
5.52 Sa se scrie formula Mac-Laurin de ordinul n pentru funct iile:
1) f (x) = e
x
, x R. 2) f(x) = sin x, x R.
3) f(x) = cos x, x R. 4) f(x) = ln(1 +x), x (1, ).
5) f(x) = (1 +x)
, x (1, ), R.
R: Avem dezvoltarile:
1) e
x
=
n
k=0
x
k
k!
+
x
n+1
(n+1)!
e
x
.
2) sin x =
n
k=1
(1)
k1 x
2k1
(2k1)!
+ (1)
n x
2n+1
(2n+1)!
sin(x).
3) cos x =
n
k=0
(1)
k x
2k
(2k)!
+ (1)
n+1 x
2n+2
(2n+2)!
cos(x).
4) ln(1 +x) =
n
k=1
(1)
k1 x
k
k
+ (1)
n x
n+1
(n+1)(1+x)
n+1
.
5) (1 + x)
= 1 +
n
k=1
(1)(k+1)
k!
x
k
+
(1)(n)
(n+1)!
x
n+1
(1 + x)
n+1
, cu
(0, 1).
5.53 Sa se determine n N astfel ca polinomul Taylor de gradul n n punctul x
0
= 0
asociat funct iei f (x) = e
x
sa aproximeze funct ia pe intervalul [1, 1] cu trei zecimale
exacte.
R: Avem
[R
n
(x)[ =
[x[
n+1
(n + 1)!
e
x
<
1
1000
, [x[ 1.
Dar cum x < 1, e
x
< e < 3 si deci [R
n
(x)[ <
3
(n+1)!
<
1
1000
pentru n 6.
5.54 Sa se scrie formula Mac-Laurin de ordinul n pentru funct ia f (x) =
a +x, a > 0,
x > a.
R: Funct ia se mai scrie: f (x) =
a
_
1 +
x
a
_1
2
. Se obt ine:
f (x) =
a
_
1 +
x
2a
+
n
k=2
(1)
k1
1 3 (2k 3)
k! 2
k
_
x
a
_
k
_
+R
n
(x) .
5.55 Sa se determine n N astfel ca valorile polinomului Taylor de gradul n n punctul
x
0
= 0 asociat funct iei f (x) =
1 +x, pe intervalul [0, 1], sa nu difere de f (x) cu mai

mult de
1
16
.
R: Avem
[R
n
(x)[ =
1 3 (2n 1)
(n + 1)! 2
n+1
x
n+1
(1 +x)
n+
1
2
1 3 (2n 1)
(n + 1)! 2
n+1
<
1
16
.
Se obt ine n 2.
5.56 Utilizand formula Mac-Laurin sa se calculeze urmatoarele limite:
1) lim
x0
e
x
+e
x
sin
2
x2
x
4
. 2) lim
x0
ln(1+2x)sin 2x+2x
2
x
3
.
3) lim
x0
sin xsin a
xa
. 4) lim
x0
1
1+x
2
cos x
tg
4
x
.
5) lim
x0
cos xe
x
2
2
x
4
.
R: 1)
1
12
. 2) 4. 3) cos a. 4)
1
3
. 5)
1
12
.
5.3 Derivatele si diferent iala funct iilor de n variabile
5.57 Utilizand denit ia, sa se calculeze derivatele part iale ale urmatoarelor funct ii, n
punctele specicate:
1) f (x, y) = x
3
3x
2
y + 2y
3
n (1, 1) . 2) f (x, y) =
xy
x+y
n (1, 1) .
3) f (x, y) =
_
sin
2
x + sin
2
y n
_
4
, 0
_
. 4) f (x, y) = ln
_
1 +x +y
2
_
n (1, 1) .
5) f (x, y) =
_
x
2
y
2
n (2, 1) . 6) f (x, y) = ln
_
x y
2
_
n (4, 1) .
R: Se obt ine:
1) f
x
(1, 1) = 3, f
y
(1, 1) = 3. 2) f
x
(1, 1) =
1
2
, f
y
(1, 1) =
1
2
.
3) f
x
_
4
, 0
_
=
1
2
2, f
y
_
4
, 0
_
= 0. 4) f
x
(1, 1) =
1
3
, f
y
(1, 1) =
2
3
.
5) f
x
(2, 1) =
2
3
, f
y
(2, 1) =
1
3
. 6) f
x
(4, 1) =
1
3
, f
y
(4, 1) =
2
3
.
5.58 Sa se calculeze derivatele part iale ale urmatoarelor funct ii:
1) f (x, y) = x
3
+y
3
3axy. 2) f (x, y) =
xy
x+y
.
3) f (x, y) =
_
x
2
y
2
. 4) f (x, y) =
x
x
2
+y
2
.
5) f (x, y) = ln
_
x +
_
x
2
+y
2
_
. 6) f (x, y) = arctg
y
x
.
7) f (x, y) = e
sin
y
x
_
x
2
y
2
x
2
+y
2
.
R: Se obt ine:
1) f
x
(x, y) = 3x
2
3ay, f
y
(x, y) = 3y
2
3ax.
2) f
x
(x, y) =
2y
(x+y)
2
, f
y
(x, y) =
2x
(x+y)
2
.
3) f
x
(x, y) =
x
x
2
y
2
, f
y
(x, y) =
y
x
2
y
2
.
4) f
x
(x, y) =
y
2
(x
2
+y
2
)
3
, f
y
(x, y) =
x
2
(x
2
+y
2
)
3
.
5) f
x
(x, y) =
1
x
2
+y
2
, f
y
(x, y) =
y
x
2
+y
2
x+
x
2
+y
2
.
6) f
x
(x, y) =
y
x
2
+y
2
, f
y
(x, y) =
x
x
2
+y
2
.
7) f
x
(x, y) =
y
x
2
e
sin
y
x
cos
y
x
, f
y
(x, y) =
1
x
e
sin
y
x
cos
y
x
.
8) f
x
(x, y) =
xy
2
(x
2
+y
2
)
x
2
y
2
, f
y
(x, y) =
x
2
2
(x
2
+y
2
)
x
2
y
2
.
1) f (x, y) = y
y
x
sin
y
x
_
x
2
y
2
x
2
+y
2
.
3) f (x, y) = arctg
x
y
. 4) f (x, y) = xyarctg
x+y
1xy
.
5) f (x, y, z) =
xyz
x
2
+y
2
+z
2
. 6) f (x, y, z) = e
x
y
e
z
y
.
7) f (x, y, z) = e
xyz
cos
y
xz
. 8) f (x, y, z) = (sin x)
yz
.
5.60 Sa e calculeze derivatele part iale ale urmatoarelor funct ii:
1) f (x, y) = ln
_
xy
2
+x
2
y
_
+
_
1 + (xy
2
+x
2
y)
2
.
2) f (x, y) =
_
1
_
x+y
xy
_
2
+ arcsin
_
x+y
xy
_
.
5.61 Sa se calculeze, utilizand denit ia, urmatoarele derivate part iale de ordinul doi:
1)

2
f
yx
(1, 1) , unde f (x, y) =
_
x
2
+y
2
. 2)

2
f
xy
(2, 2) , unde f (x, y) =
3
_
x
2
y.
3)

2
f
xy
_
4
, 0
_
, unde f (x, y) = xsin (x +y) . 4)

2
f
xy
(1, 1) , unde f (x, y) = xy ln x.
R: 1) Deoarece
2
f
yx
(1, 1) = lim
y1
f
x
(1, y)
f
x
(1, 1)
y 1
,
se obt ine
1
2
2
. 2)
1
9
. 3)
2
2
_
1

4
_
. 4) 1.
1) f (x, y, z) = x
3
y
2
z + 2x 3y +z + 5. 2) f (x, y, z) = (xy)
z
.
3) f (x, y, z) =
_
x
2
+y
2
+z
2
. 4) f (x, y, z) = z
xy
.
R: Se obt ine:
1) f
x
(x, y, z) = 3x
2
y
2
z + 2, f
y
(x, y, z) = 2x
3
yz 3, f
z
(x, y, z) = x
3
y
2
+ 1.
2) f
x
(x, y, z) =
z
x
(xy)
z
, f
y
(x, y, z) =
z
y
(xy)
z
, f
z
(x, y, z) = (xy)
z
ln (xy).
3) f
x
(x, y, z) =
x
x
2
+y
2
+z
2
, f
y
(x, y, z) =
y
x
2
+y
2
+z
2
,
f
z
(x, y, z) =
z
x
2
+y
2
+z
2
.
4) f
x
(x, y, z) = y z
xy
ln z, f
y
(x, y, z) = xz
xy
ln z, f
z
(x, y, z) =
xy
z
z
xy
.
5.63 Sa se arate ca urmatoarele funct ii sunt omogene si apoi sa se verice relat ia lui
Euler:
1) f (x, y) = ax
2
+ 2bxy +cy
2
. 2) f (x, y) =
x+y
3
x
2
+y
2
.
3) f (x, y) =
x
x
2
+y
2
. 4) f (x, y) =
_
x
2
y
2
_
ln
xy
x+y
.
5) f (x, y) =
_
x
2
+y
2
_
sin
y
x
. 6) f (x, y) =
_
x
2
y
2
_
e
y
x
.
5.64 Sa se arate ca daca u = f (x, y, z) este o funct ie omogena de gradul de omogenitate
m, care admite derivate part iale de ordinul doi continue pe T R
3
, atunci:
1) x
2
f
x
2
+y

2
f
xy
+z

2
f
xz
= (m1)
f
x
.
2) x
2
2
f
x
2
+y
2
2
f
y
2
+z
2
2
f
z
2
+ 2xy

2
f
xy
+ 2yz

2
f
yz
+ 2zx

2
f
zx
= m(m1) f.
5.65 Sa se arate ca funct iile date mai jos satisfac egalitat ile scrise n dreptul lor:
1) z = ln
_
x
2
+xy +y
2
_
, x
z
x
+y
z
y
= 2.
2) z = xy +xe
y
x
, x
z
x
+y
z
y
= xy +z.
3) u = (x y) (y z) (z x) ,
u
x
+
u
y
+
u
z
= 0.
4) u = x +
x y
y z
,
u
x
+
u
y
+
u
z
= 1.
5) u = ln
_
x
3
+y
3
+z
3
3xyz
_
,
u
x
+
u
y
+
u
z
=
1
x +y +z
.
5.66 Se da funct ia:
f (x, y) =
_
y
2
ln
_
1 +
x
2
y
2
_
, y ,= 0,
0, y = 0.
Sa se arate ca desi nu sunt satisfacute ipotezele teoremei lui Schwarz, totusi
2
f
xy
(0, 0) =

2
f
yx
(0, 0) .
R: Sa observam ca teorema lui Schwarz da condit ii suciente nu si necesare pentru
egalitatea derivatelor mixte.
Deoarece pentru x > 1, ln x > x, avem
0 < y
2
ln
_
1 +
x
2
y
2
_
= 2y
2
ln
1 +
x
2
y
2
< 2y
2
1 +
x
2
y
2
= 2 [y[
_
x
2
+y
2
,
deci
lim
(x,y)(0,0)
f (x, y) = f (x, y) = 0,
apoi
f
x
(x, y) =
_
2xy
2
x
2
+y
2
, y ,= 0,
0, y = 0,
f
y
(x, y) =
_
2y ln
_
1 +
x
2
y
2
_
2xy
2
x
2
+y
2
, y ,= 0,
0, y = 0,
si
2
f
xy
(0, 0) = lim
x0
f
x
(x, 0)
f
x
(0, 0)
x
= 0,
2
f
yx
(0, 0) = lim
y0
f
x
(0, y)
f
x
(0, 0)
y
= 0.
Dar
2
f
yx
(x, y) =
_
4x
3
y
(x
2
+y
2
)
2
, y ,= 0,
0, y = 0,
nu este continua n origine.
5.67 Sa se calculeze derivatele part iale de ordinul doi ale funct iilor:
1) f (x, y) = 2x
2
3xy y
2
. 2) f (x, y) =
_
x
2
a
2
+
y
2
b
2
.
3) f (x, y) = ln
_
x
2
+y
_
. 4) f (x, y) =
_
2xy +y
2
.
5) f (x, y) = arctg
x+y
1xy
. 6) f (x, y) = (arcsin xy)
2
.
7) f (x, y, z) =
_
x
2
+y
2
+z
2
. 8) f (x, y, z) = xy +yz +zx.
5.68 Sa se calculeze derivatele part iale de ordinul doi, n origine, ale funct iei:
f (x, y) = (1 +x)
m
(1 +y)
n
.
R: f
xx
(0, 0) = m(m1), f
xy
(0, 0) = mn, f
yy
(0, 0) = n(n 1).
5.69 Sa se calculeze derivatele part iale de ordinul m+n:
m+n
f
m
yx
n
(x, y) , unde : 1) f (x, y) =
x +y
x y
. 2) f (x, y) =
_
x
2
+y
2
_
e
x+y
.
R: 1) Prin induct ie dupa n si apoi dupa m, se obt ine:
m+n
f
y
m
x
n
(x, y) = (1)
n
2 (m+n 1)!
mx +ny
(x y)
m+n+1
.
2) Se obt ine:
m+n
f
y
m
x
n
(x, y) =
_
x
2
+y
2
+ 2 (mx +ny) +m(m1) +n(n 1)
e
x+y
.
5.70 Sa se arate ca funct iile:
1) u = arctg
y
x
, 2) u = ln
1
r
, unde r =
_
(x a)
2
+ (y b)
2
,
satisfac ecuat ia lui Laplace:
2
u
x
2
+

2
u
y
2
= 0.
5.71 Sa se arate ca funct ia u = Asin (at +) sin x satisface ecuat ia undelor:
2
u
t
2
a
2
2
u
x
2
= 0.
u =
1
_
t
_
3
e
x
2
+y
2
+z
2
t
satisface ecuat ia caldurii:
u
t
=
1
4
_
2
u
x
2
+

2
u
y
2
+

2
u
z
2
_
.
5.73 Se da funct ia f (x, y) = x
2
+xyy
2
. Sa se gaseasca variat ia si diferent iala funct iei
n punctul (x
0
, y
0
).
R: Variat ia funct iei este:
f (x, y) f (x
0
, y
0
) = [(2x
0
+y
0
) h + (x
0
2y
0
) k] +
_
h
2
+hk k
2
_
.
Deci diferent iala este df (x
0
, y
0
) = (2x
0
+y
0
) h + (x
0
2y
0
) k.
5.74 Se da funcatia f (x, y) = x
2
y. Sa se calculeze variat ia si diferent iala funct iei n
punctul (x
0
, y
0
) = (1, 2), pentru: 1) (h, k) = (1, 2), 2) (h, k) = (0, 1; 0, 2).
5.75 Utilizand denit ia, sa se arate ca urmatoarele funct ii sunt diferent iabile n punctele
specicate:
1) f (x, y) = (x 1)
2
+y
2
n (1, 1) . 2) f (x, y) = x
2
+ (y 2)
2
n (1, 1) .
3) f (x, y) =
z
x
2
+y
2
n (3, 4, 5) . 4) f (x, y) = ln
_
x
3
+y
3
_
n (0, 1) .
R: 1) Pentru orice (h, k) R
2
, avem
f (1 +h, 1 +k) f (1, 1) = 2k +
_
h
2
+k
2
_
= 2k +(k, h)
_
h
2
+k
2
,
cu (k, h) =
h
2
+k
2
0, pentru (k, h) (0, 0), iar df (1, 1) = 2k.
5.76 Sa se arate ca n origine, funct ia
f (x, y) =
_
xy
x
2
+y
2
, x
2
+y
2
,= 0,
0, x
2
+y
2
= 0,
este continua, admite derivate part iale, nsa nu este diferent iabila.
R: Din
0 <
[xy[
_
x
2
+y
2
<
[xy[
_
y
2
= [x[ ,
deducem ca f este continua n origine. Utilizand denit ia se arata ca funct ia are derivate
part iale n origine egale cu 0.
Sa aratam ca funct ia nu este diferent iabila n origine. Daca ar diferent iabila n
origine, ar avea loc egalitatea:
f (x, y) 0 = 0 (x 0) + 0 (y 0) +(x, y)
_
x
2
+y
2
,
n care (x, y) sa aiba limita n origine egala cu 0. Dar din egalitatea precedenta rezulta
(x, y) =
xy
x
2
+y
2
, funct ie care nu are limita n origine.
5.77 Sa se cerceteze daca funct ia f (x, y) =
_
x
2
+y
2
este diferent iabila n origine.
R: Funct ia nu admite derivate part iale n origine, deci nu este diferent iabilan origine.
1) f (x, y) = x
3
+y
3
3xy. 2) f (x, y) = x
2
y
3
.
3) f (x, y) =
x
2
y
2
x
2
+y
2
. 4) f (x, y) = sin
2
x + sin
2
y.
5) f (x, y) = ln
_
x
2
+y
2
_
. 6) f (x, y) = arctg
y
x
+ arctg
x
y
.
R: 1) df (x, y) =
_
3x
2
3y
_
dx +
_
3y
2
3x
_
dy.
1) f (x, y, z) = xyz. 2) f (x, y, z) =
_
x
2
+y
2
+z
2
.
3) f (x, y, z) = arctg
xy
z
2
. 4) f (x, y, z) =
_
xy +
x
y
_
z
.
R: df (x, y, z) = yz dx +zxdy +xy dz.
5.80 Sa se gaseasca cu cat se modica (aproximativ) volumul unui con avand raza bazei
x = 10 cm si nalt imea y = 30 cm daca raza se micsoreaza cu 1 mm, iar nalt imea creste
cu 3 mm.
R: Volumul conului este V =

3
x
2
y. Variat ia volumului este data de:
V V
0
dV =

3
_
2xy dx +x
2
dy
_
=

3
(600 0, 1 + 100 0, 3) = 10 cm
3
.
5.81 Sa se calculeze aproximativ (1, 02)
3,01
.
R: Consideram funct ia z = x
y
. Luam x
0
= 1, y
0
= 3, h = 0, 02 si k = 0, 01. Putem
scrie:
z z
0
dz = x
y
0
1
0
y
0
h +x
y
0
0
ln x
0
k = 3 0, 02 + 0 0, 01 = 0, 06.
Deci z 1 + 0, 06 = 1, 06.
5.82 Sa se calculeze diferent ialele de ordinul doi ale funct iilor:
1) f (x, y) = cos xy. 2) f (x, y) =
_
x
2
+y
2
. 3) f (x, y) = e
xy
.
4) f (x, y) = ln xy. 5) f (x, y, z) = xyz. 6) f (x, y, z) = e
x
sin yz.
R: 1) d
2
f (x, y) =
_
y
2
dx
2
+ 2xy dxdy +x
2
dy
2
_
cos xy.
5.83 Sa se calculeze diferent iala de ordinul doi a funct iei f(x, y, z) = sin (x 2y +z).
5.84 Sa se calculeze diferent iala de ordinul n a funct iei f (x, y) = e
ax+by
.
R: Se obt ine: d
n
f (x, y) = e
ax+by
(a dx +b dy)
n
.
5.85 Aplicand formula de derivare a funct iilor compuse, sa se calculeze F
(x
0
), stiind
ca F (x) = f (u(x) , v (x)) n care:
1) f (u, v) = u +uv, u(x) = cos x, v (x) = sin x, x
0
=

4
.
2) f (u, v) = e
u2v
, u(x) = x
2
, v (x) = x
2
2, x
0
= 2.
5.86 Sa se gaseasca
dz
dt
daca:
1) z = e
3x+2y
, x = cos t, y = t
2
.
2) z =
x
y
, x = e
t
, y = ln t.
3) z = ln sin
x
y
, x = 3t
2
, y =
t
2
+ 1.
5.87 Sa se gaseasca
dz
dt
daca:
1) z = e
x
2
+y
2
, x = a cos t, y = a sin t. 2) z =
1
2
ln
x
y
, x = tg
2
t, y = ctg
2
t.
5.88 Sa se gaseasca
du
dt
daca:
1) u = xyz, x = t
2
+ 1, y = ln t, z = tg t.
2) u =
z
x
2
+y
2
, x = Rcos t, y = Rsin t, z = H.
5.89 Sa se gaseasca
dz
dx
daca z = u
v
, unde u = sin x, v = cos x.
5.90 Sa se gaseasca
z
x
si
dz
dx
daca z = x
y
, unde y = (x).
5.91 Sa se gaseasca
z
x
si
z
y
, daca z = f (u, v), unde u = x
2
+y
2
si v = e
xy
.
5.92 Sa se gaseasca
z
u
si
z
v
, daca z = arctg
x
y
, unde x = usin v si y = ucos v.
5.93 Sa se gaseasca
z
u
si
z
v
, daca z = f (u), unde u = xy +
y
x
.
5.94 Sa se arate ca daca = f
_
x
2
+y
2
+z
2
_
, unde:
x = Rcos ucos v, y = Rcos usin v, z = Rsin u,
atunci:

u
= 0 si

v
= 0.
5.95 Sa se arate ca daca z = f (x +ay), unde f este o funct ie diferent iabila, atunci
z
y
= a
z
x
.
5.96 Sa se arate ca funct ia w = f (u, v), unde f este o funct ie diferent iabila si u =
x +at, v = y +bt, satisface ecuat ia:
w
t
= a
w
x
+b
w
y
.
5.97 Sa se arate ca funct ia z = yf
_
x
2
y
2
_
, unde f este o funct ie diferent iabila,
satisface ecuat ia:
1
x
z
x
+
1
y
z
y
=
z
y
2
.
5.98 Sa se arate ca funct ia z = xy+f
_
y
x
_
, unde f este o funct ie diferent iabila, satisface
ecuat ia:
x
z
x
+y
z
y
= xy +z.
5.99 Sa se arate ca funct ia z = e
y
f
_
ye
x
2
2y
2
_
, unde f este o funct ie diferent iabila,
satisface ecuat ia:
_
x
2
y
2
_
z
x
+xy
z
y
= xyz.
5.100 Sa se arate ca funct ia z = xf
_
y
x
_
+g
_
y
x
_
, unde f si g sunt o funct ii de doua ori
diferent iabile, satisface ecuat ia:
x
2
2
z
x
2
+ 2xy

2
z
xy
+y
2
2
z
y
2
= 0.
5.101 Sa se arate ca funct ia z = f (xy) +
xy g
_
y
x
_
, unde f si g sunt o funct ii de
doua ori diferent iabile, satisface ecuat ia:
x
2
2
z
x
2
y
2
2
z
y
2
= 0.
5.102 Sa se arate ca funct ia z = f (x +g (y)) satisface ecuat ia:
z
x
2
z
xy
=
z
y
2
z
x
2
.
5.103 Sa se gaseasc a d
2
z daca:
1) z = f (u) , u = x
2
+y
2
. 2) z = u
v
, u =
x
y
, v = xy.
3) z = f (u, v) , u = ax, v = ay. 4) z = f (u, v) , u = xe
y
, v = ye
x
.
5.104 Sa se calculeze diferent ialele de ordinul doi ale funct iilor compuse:
1) F (x) = f
_
x
2
, ln x
_
. 2) F (x, y) = f
_
x
2
,
x
y
_
.
3) F (x, y, z) = f
_
x +y +z, x
2
+y
2
+z
2
_
.
5.105 Sa se gaseasc a polinomul Taylor de gradul 3 asociat funct iei
f(x, y) =
_
x
2
+y
2
n punctul (1, 1).
R:Polinomul Taylor de gradul 3 asociat funct iei f este:
T
3
(x, y) =
2 +
1
1!
1
2
[(x 1) +(y 1)] +
1
2!
1
2
2
[(x 1)
2
2(x 1)(y 1) +(y 1)
2
]
1
3!
1
4
2
[(x 1)
3
(x 1)
2
(y 1) (x 1)(y 1)
2
+ (y 1)
3
].
5.106 Sa se gaseasca polinomul Taylor de gradul n asociat funct iei f(x, y) = e
x+y
n
punctul (1, 1).
R: Avem:
T
n
(x, y) = 1 +
n
k=1
1
k!
[(x 1) + (y + 1)]
k
=
n
k=0
k
i=0
1
i!(k i)!
(x 1)
ki
(y + 1)
i
.
5.107 Sa se gaseasc a o valoare aproximativa a numarului (1, 1)
1,2
.
R: Polinomul Taylor de gradul 3 asociat funct iei f(x, y) = x
y
, x > 0, y > 0, n
punctul (1, 1) este:
T
3
(x, y) = 1 +
1
1!
(x 1) +
1
2!
[2(x 1)(y 1)] +
1
3!
[3(x 1)
2
(y 1)].
Putem atunci scrie f(1, 1; 1, 2) T
3
(1, 1; 1, 2) = 1, 1021.
5.108 Sa se dezvolte polinomul
f (x, y) = x
3
2y
3
+ 3xy
dupa formula lui Taylor n vecin atatea punctului (1, 2).
R: Avem:
f (x, y) = 9 (x 1) 21 (y 2) + 3 (x 1)
2
+ 3 (x 1) (y 2) 12 (y 2)
2
+
+(x 1)
3
2 (y 2)
3
.
5.109 Sa se dezvolte polinomul
f (x, y) = x
2
+ 2xy + 3y
2
6x 2y 4
dupa formula lui Taylor n vecin atatea punctului (2, 1).
R: f (x, y) = 1 (x + 2)
2
+ 2 (x + 2) (y 1) + 3 (y 1)
2
.
5.110 Sa se dezvolte polinomul f (x, y, z) = x
2
+y
2
+z
2
+ 2xy yz 4x 3y z + 4
dupa formula lui Taylor n vecin atatea punctului (1, 1, 1).
5.111 Se da polinomul f (x, y, z) = x
2
+ y
2
+ z
2
2xy 2xz 2yz. Sa se dezvolte
f (x +k, y +h, z +) dupa formula lui Taylor n vecin atatea punctului (x, y, z).
5.112 Sa se gaseasc a polinoamele Taylor de gradul 3 asociate, n origine, funct iilor:
1) f (x, y) = e
x
sin y. 2) f (x, y) = cos xcos y.
R: 1) T
3
(x, y) = y +xy
1
6
y
3
+
1
2
x
2
y. 2) T
3
(x, y) = 1
1
2
y
2
1
2
x
2
.
5.113 Sa se gaseasc a polinomul Taylor de gradul 2 asociat funct iei
f (x, y) =
_
x
2
+y
2
n punctul (1, 1).
R: Avem
T
3
(x, y) =
2+
2
1!
[(x 1) + (y 1)]+
1
2!
1
2
2
_
(x 1)
2
2 (x 1) (y 1) + (y 1)
2
_
.
5.114 Sa se deduca formule aproximative (exacte pan a la termeni de gradul doi n x si
y) pentru funct iile:
1) f (x, y) = arctg
1x
1y
, 2) f (x, y) =
_
(1+x)
m
+(1+y)
n
2
,
daca [x[ si [y[ sunt mici n comparat ie cu unitatea.
Capitolul 6
Funct ii denite implicit
6.1 Funct ii denite implicit de o ecuat ie
6.1 Sa se arate ca ecuat ia F (x; y) = y
3
xy
2
xy +x
2
= 0:
1) Admite o innitate de solut ii y = f (x), f : [0, ) [0, ).
2) Admite numai patru solut ii continue y = f (x), f : [0, ) [0, ).
3) Exista o vecinatate U a punctului x
0
= 4 si o vecinatate V a punctului y
0
= 2, n
care ecuat ia F (x; y) = 0 admite o singura solut ie y = f (x), f : U V , continu a pe U,
care satisface condit ia f (4) = 2.
R: 1) Ecuat ia se mai scrie: (y x)
_
y
2
x
_
= 0. Deci, pentru orice , R, cu
0 , funct iile y = f (x), f : [0, ) [0, ), denite prin:
f (x) =
_
x, x [, ),
x, n rest,
f (x) =
_
x, x [, ),
x, n rest.
2) Cele patru solut ii continue pe [0, ) sunt:
f
1
(x) = x, f
2
(x) =
x, f
3
(x) =
_
x, x [0, 1),
x, x [1, ),
f
4
(x) =
_
x, x [0, 1),
x, x [1, ).
3) Deoarece F
y
(4; 2) = 8 ,= 0, daca luam U = (1, ) si V = (1, ), funct ia
f (x) =
x este continua si f (4) = 2.

6.2 Sa se arate ca ecuat ia F (x, y; z) = x
2
+ y
2
z
2
3xyz = 0 admite numai doua
solut ii z = z
1
(x, y) si z = z
2
(x, y) continue si diferent iabile pe o vecinatate a punctului
(0, 1).
R: Ecuat ia F (0, 1; z) = 1 z
2
= 0 are radacinile z
1
= 1 si z
2
= 1, iar F
z
(x, y; z) =
(2z + 3xy), a.. F
z
(0, 1; 1) = 2, F
z
(0, 1; 1) = 2. Deci exista doua funct ii continue
si diferent iabile pe o vecinatate a punctului (0, 1) care satisfac condit iile z
1
(0, 1) = 1 si
respectiv z
2
(0, 1) = 1. Derivatele lor part iale sunt date de:
z
x
=
2x 3yz
2z + 3xy
,
z
y
=
2y 3xz
2z + 3xy
.
75
CAPITOLUL 6. FUNCT II DEFINITE IMPLICIT 76
Valorile lor n punctul (0, 1) sunt:
z
1
x
(0, 1) =
3
2
,
z
1
y
(0, 1) = 1,
z
2
x
(0, 1) =
3
2
,
z
2
y
(0, 1) = 1.
6.3 Sa se calculeze
dy
dx
si
d
2
y
dx
2
daca
1) F (x; y) =
_
x
2
+y
2
_
3
3
_
x
2
+y
2
_
+ 1 = 0.
2) F (x; y) = ln
_
x
2
+y
2
a arctg
y
x
= 0, a ,= 0.
3) F (x; y) = x
2
+y
2
+ ln
_
x
2
+y
2
_
a
2
= 0.
R: 1)
dy
dx
=
x
y
si
d
2
y
dx
2
=
x
2
+y
2
y
3
. 2)
dy
dx
=
x+ay
axy
,
d
2
y
dx
2
=
(a
2
+1)(x
2
+y
2
)
(axy)
3
.
3)
dy
dx
=
x
y
,
d
2
y
dx
2
=
x
2
+y
2
y
3
.
6.4 Sa se calculeze
dy
dx
,
d
2
y
dx
2
si
d
3
y
dx
3
daca
x
2
a
2
+
y
2
b
2
1 = 0.
R:
dy
dx
=
b
2
x
a
2
y
,
d
2
y
dx
2
=
b
4
a
2
y
3
si
d
3
y
dx
3
=
3b
6
x
a
4
y
5
.
6.5 Sa se calculeze
dy
dx
daca F (x; y) = y
x
y + 1 = 0.
R:
dy
dx
=
y
x
ln x
1xy
x1
.
6.6 Ecuat iile:
1) F (x, y; z) = x
3
+ 2y
3
+z
3
3xyz 2y + 3 = 0,
2) F (x, y; z) = xcos y +y cos x +z cos x 1 = 0,
3) F (x, y; z) = x +y +z e
z
= 0,
4) F (x, y; z) = z
2
xe
y
ye
z
ze
x
= 0,
denesc funct ii z = z (x, y). Sa se calculeze:
z
x
si
z
y
.
R: 1)
z
x
=
x
2
yz
xyz
2
,
z
y
=
6y
2
3xz2
3(xyz
2
)
.
2)
z
x
=
z cos xcos y
cos xy sin z
,
z
y
=
x sin ycos z
cos xy sin z
.
3)
z
x
=
z
y
=
1
e
z
1
. 4)
z
x
=
e
y
+ze
x
2zye
z
e
x
,
z
y
=
xe
y
+e
z
2zye
z
e
x
.
6.7 Ecuat iile:
1) xe
y
+ye
x
+ze
x
= 1, 2) x z + arctg
y
z x
= 0, 3) sin xy e
xy
x
2
y = 0.
denesc funct ii z = z (x, y). Sa se calculeze
z
x
.
R: 1)
z
x
= y z e
yx
. 2)
z
x
= 1. 3)
z
x
=
y(e
xy
+2xcos xy)
x(e
xy
+xcos xy)
.
6.8 Sa se calculeze derivatele part iale de ordinul ntai si cele de ordinul al doilea ale
funct iei z = z (x, y) denita de ecuat ia
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1 = 0.
R:
z
x
=
c
2
x
a
2
z
,
z
y
=
c
2
y
b
2
z
,

2
z
x
2
=
c
4
(b
2
y
2
)
a
2
b
2
z
3
,

2
z
xy
=
c
4
xy
a
2
b
2
z
3
,

2
z
y
2
=
c
4
(a
2
x
2
)
a
2
b
2
z
3
.
6.9 Sa se calculeze dz si d
2
z daca funct ia z = z (x, y) este denita de ecuat ia:
x
2
+y
2
+z
2
= a
2
.
R: dz =
x
z
dx
y
x
dy, d
2
z =
y
2
a
2
z
3
dx
2
2
xy
z
3
dxdy +
x
2
a
2
z
3
dy
2
.
6.10 Sa se calculeze dz si d
2
z n punctul (2, 0; 1) daca funct ia z = z (x, y) este denita
de ecuat ia:
2x
2
+ 2y
2
+z
2
8xz z + 8 = 0.
R: dz (2, 0) = 0, d
2
z (2, 0) =
4
15
_
dx
2
+dy
2
_
.
6.11 Funct ia z = z (x, y) este denita de ecuat ia (y +z) sin z y (x +z) = 0. Sa se
arate ca
z sin z
z
x
y
2
z
y
= 0.
R: Avem:
z
x
=
y
sinz +y cos z +z cos z y
,
z
y
=
sin z x z
sinz +y cos z +z cos z y
.
6.12 Funct ia z = z (x, y) este denita de ecuat ia x
2
+y
2
+z
2
= (ax +by +cz), unde
este o funct ie derivabila si a, b, c sunt constante. Sa se arate ca
(cy bz)
z
x
+ (az cx)
z
y
= bx ay.
6.13 Funct ia z = z (x, y) este denita de ecuat ia F (x az, y bz) = 0, unde F este o
funct ie diferent iabila iar a si b sunt constante. Sa se arate ca
a
z
x
+b
z
y
= 1.
6.14 Ecuat ia F (x + 2y, y 2x) = 0 deneste funct ia y = y (x). Sa se calculeze y
(x)
si y
(x).
6.15 Ecuat ia F (sin x +y, cos y +x) = 0 deneste funct ia y = y (x). Sa se calculeze
y
(x) si y
(x).
6.16 Ecuat ia
ln
_
x
2
+y
2
+z
2
_
+ arcsin (ax +by +cz) = 1
deneste funct ia z = z (x, y). Sa se calculeze
z
x
,
z
y
,

2
z
xy
.
6.17 Ecuat ia F
_
x +
z
y
, y +
z
x
_
= 0 deneste funct ia z = z (x, y). Sa se arate ca:
x
z
x
+y
z
y
= z xy.
6.18 Ecuat ia F
_
x
z
,
y
z
_
= 0 deneste funct ia z = z (x, y). Sa se arate ca:
x
z
x
+y
z
y
= z.
6.2 Funct ii denite implicit de un sistem de ecuat ii
6.19 Sistemul
_
F(x; y, z) = x
2
+y
2
z
2
= 0,
G(x; y, z) = x
2
+ 2y
2
+ 3z
2
5 = 0,
deneste funct iile y = y (x), z = z (x). Sa se calculeze y
(x), z
(x), y
(x) si z
(x).
R: Din sistemul: x+yy
zz
= 0, x+2yy
+3zz
= 0, se obt ine: y
=
4x
5y
, z
=
x
5z
.
Derivand din nou si nlocuind y
si z
, obt inem:
y
=
4
25
5y
2
+ 4x
2
y
3
, z
=
1
25
x
2
5z
2
z
3
.
6.20 Sistemul
_
F(x; y, z) = cos x + cos y + cos z a = 0,
G(x; y, z) = x
3
+y
3
+z
3
b = 0,
deneste funct iile y = y (x), z = z (x). Sa se calculeze y
(x), z
(x).
R: Din sistemul: sin x +y
siny z
sin z = 0, x
2
+y
2
y
+z
2
z
= 0, obt inem:
y
=
x
2
sin z z
2
sin x
y
2
sin z z
2
sin y
, z
=
x
2
sin y y
2
sin x
z
2
sin y y
2
sin z
.
6.21 Sistemul xyz = a, x + y + z = b deneste funct iile y = y (x), z = z (x). Sa se
calculeze dy, dz, d
2
y si d
2
z.
R: Din: yzdx +xzdy +xydz = 0 si dx +dy +dz = 0 se obt ine:
dy =
y (x z)
x(y z)
dx, dz =
z (x y)
x(y z)
dx,
d
2
y = d
2
z = 2yz
x
2
+y
2
+z
2
xz xy yz
x
2
(y z)
3
dx
2
.
6.22 Sistemul
_
F(x, y; u, v) = u +v x y = 0,
G(x, y; u, v) = xu +yv 1 = 0,
pentru x ,= y, deneste pe u si v ca funct ii de x si y. Sa se calculeze derivatele part iale
ale funct iilor u = u(x, y) si v = v(x, y).
R: Pentru a calcula derivatele part iale ale funct iilor u = u(x, y) si v = v(x, y), derivam
cele doua ecuat ii n raport cu x si apoi cu y. Se obt in sistemele liniare:
_
u
x
+v
x
= 1,
xu
x
+yv
x
= u,
_
u
y
+v
y
= 1,
xu
y
+yv
y
= v,
al caror determinant este
D(F, G)
D(u, v)
=
1 1
x y
= y x ,= 0.
Aplicand regula lui Cramer se obt ine:
u
x
=
y +u
y x
, v
x
=
x +u
y x
, u
y
=
y +v
y x
, v
y
=
x +v
y x
.
6.23 Sistemul
_
F(x, y; u, v) = u x y = 0,
G(x, y; u, v) = uv y = 0,
deneste pe u si v ca funct ii de x si y. Sa se calculeze derivatele part iale de ordinul ntai
si doi ale funct iilor u = u(x, y) si v = v(x, y).
6.24 Sistemul
_
F(x, y; u, v) = x +y +u +v a = 0,
G(x, y; u, v) = x
3
+y
3
+u
3
+v
3
b = 0,
deneste pe u si v ca funct ii de x si y. Sa se calculeze derivatele part iale de ordinul ntai
si doi ale funct iilor u = u(x, y) si v = v(x, y).
R: Obt inem:
u
x
=
v
2
x
2
u
2
v
2
, v
x
=
x
2
u
2
u
2
v
2
, u
y
=
v
2
y
2
u
2
v
2
, v
y
=
y
2
u
2
u
2
v
2
.
6.25 Sistemul
_
F(x, y; u, v) = u +v x = 0,
G(x, y; u, v) = u yv = 0,
deneste pe u si v ca funct ii de x si y. Sa se calculeze du, dv, d
2
u si d
2
v.
R: Din: du +dv = dx si du y dv = v dy, se obt ine:
du =
1
1 +y
(y dx +v dy) , dv =
1
1 +y
( dx v dy) ,
d
2
u = d
2
v =
2
(1 +y)
2
_
dxdy v d
2
y
_
.
6.26 Sistemul (u, v) = x, (u, v) = y deneste pe u si v ca funct ii de x si y. Sa se
calculeze
u
x
,
v
x
,
u
y
,
v
y
.
R: Derivand cele doua ecuat ii n raport cu x, obt inem:
u
u
x
+

v
v
x
= 1,

u
u
x
+

v
v
x
= 0.
Daca
D(,)
D(u,v)
,= 0, obt inem:
u
x
=
u
D(,)
D(u,v)
,
v
x
=
v
D(,)
D(u,v)
.
6.27 Sa se gaseasca z
x
si z
y
daca:
1) x = ucos v, y = usin v, z = cv. 2) x = u +v, y = u v, z = uv.
R: 1) z
x
= cv
x
=
cy
x
2
+y
2
, z
y
= cv
y
=
cx
x
2
+y
2
. 2) z
x
=
1
2
x, z
y
=
1
2
y.
6.3 Transformari punctuale
6.28 Fie E = (0, ) [0, 2) R
2
si F = R
2
(0, 0). Sa se arate ca transformarea
punctuala:
x = r cos , y = r sin , (r, ) E,
este regulata pe E si sa se determine inversa sa n vecinatatea punctului
_
1,

4
_
E.
R: Determinantul funct ional al transformarii este
D(x, y)
D(r, )
=
cos r sin
sin r cos
= r ,= 0, (r, ) E.
Deci n orice punct cu except ia originii, transformarea este regulata si inversa ei este
r =
_
x
2
+y
2
, = arctg
y
x
.
6.29 Fie E = (0, ) [0, 2) R R
3
si F = R
3
(0, 0, z) , z R. Sa se arate ca
transformarea punctuala:
x = r cos , y = r sin , z = z,
_
1,

4
, 0
_
E.
D(x, y, z)
D(r, , z)
=
cos r sin 0
sin r cos 0
0 0 1
= r ,= 0, (r, , z) E.
Deci n orice punct cu except ia celor de pe axa Oz este regulata si inversa ei este
r =
_
x
2
+y
2
, = arctg
y
x
, z = z.
6.30 Fie E = (0, ) [0, 2) (0, ) R
3
si F = R
3
(0, 0, z) , z R. Sa se arate
ca transformarea punctuala:
x = r cos sin , y = r sin sin , z = r cos , (r, , ) E,
_
1,

4
, 0
_
E.
D(x, y, z)
D(r, , z)
=
sin cos r cos cos r sin sin

sin sin r cos sin r sin cos
cos r sin 0
= r
2
sin ,= 0.
Deci n orice punct cu except ia celor de pe axa Oz este regulata si inversa ei este
r =
_
x
2
+y
2
+z
2
, = arctg
y
x
, = arccos
z
_
x
2
+y
2
+z
2
.
6.31 Se da transformarea punctuala f : R
2
R
2
denita prin:
u = x
2
+y
2
, v = x
2
y
2
.
1) Sa se gaseasca imaginea mult imii E =
_
(x, y) R
2
[ x > 0, y > 0
_
prin transfor-
marea f .
2) Sa se arate ca transformarea f este regulata ntr-o vecinatate a punctului (1, 1).
3) Sa se gaseasca inversa transformarii f .
R: 1) F =
_
(u, v) R
2
u +v > 0, u v > 0
_
. 2)
D(u,v)
D(x,y)
(1, 1) = 8 ,= 0. 3) Inversa
transformarii f este:
x =
1
u +v, y =
1
u v.
6.32 Sa se arate ca transformarea punctuala f : R
2
R
2
denita prin:
u = sin (x +y) , v = y
3
,
nu este regulata pe mult imea D =
_
4
,

4
4
,

4
.
R:
D(u,v)
D(x,y)
= 3y
2
cos (x +y) = 0 pentru y = 0 sau x +y =
2
.
6.33 Sa se arate ca transformarea:
x = cos cos , y = cos sin ,
este regulata pe mult imea E =
_
(, ) [ 0 < <

2
, R
_
. Sa se calculeze:
x
,

x
,

y
,

y
,
n punctul (x
0
, y
0
) =
_
1
2
,
1
2
_
, imaginea prin transformarea data a punctului (
0
,
0
) =
_
4
,

4
_
.
D(x, y)
D(, )
=
sin cos cos sin

sinsin cos cos
= 2 sin cos ,= 0, (, ) E.
Inversa transformarii este: = arccos
_
x
2
+y
2
, = arctg
y
x
, iar:
x
_
1
2
,
1
2
_
=

x
_
1
2
,
1
2
_
=

y
_
1
2
,
1
2
_
=

y
_
1
2
,
1
2
_
= 1.
6.34 Fie transformarea: x = r cos sin , y = r sin sin , z = r cos , (r, , ) R
3
.
1) Sa se determine punctele n care transformarea este regulata.
2) Sa se calculeze jacobianul transformarii inverse si derivatele r
xx
,
yy
,
zz
n
punctul (x
0
, y
0
, z
0
) = (0, 1, 0).
R: 1) Jacobianul transformarii este:
D(x, y, z)
D(r, , )
=
cos sin r sin sin r cos cos

sin sin r cos sin r sin cos
cos 0 r sin
= r
2
sin .
Transformarea este regulata daca r ,= 0 si ,= k, k Z.
2) Jacobianul transformarii inverse n punctul (0, 1, 0) este:
D(r, , )
D(x, y, z)
(0, 1, 0) =
1
D(x,y,z)
D(r,,)
_
1,

2
,

2
_ = 1.
Transformarea inversa este:
r =
_
x
2
+y
2
+z
2
, = arctg
y
x
, = arccos
z
_
x
2
+y
2
+z
2
.
Iar: r
xx
(0, 1, 0) = 1,
yy
(0, 1, 0) = 0,
zz
(0, 1, 0) = 1.
6.4 Dependent a si independent a funct ionala
1) f (x, y, z) = x +y +z, g (x, y, z) = x
2
+y
2
+z
2
, h(x, y, z) = xy +xz +yz.
2) f (x, y, z) = x +y +z, g (x, y, z) = x y +z, h(x, y, z) = 4xy + 4yz.
sunt funct ional dependente pe R
3
.
R: 1) Matricea funct ionala
_
_
x y z
2x 2y 2z
y +z x +z x +y
_
_
are rangul mai mic decat 3. Relat ia de dependent a funct ionala este: g = f
2
2h.
2) Matricea funct ionala
_
_
1 1 1
1 1 1
4y 4x + 4z 4y
_
_
are rangul mai mic decat 3. Relat ia de dependent a funct ionala este: h = f
2
g
2
.
f (x, y, z) = ln
_
x
2
+y
2
+z
2
_
,
g (x, y, z) = arctg
_
x
y

y
x
+z
_
,
sunt funct ional independente pentru x > 0, y > 0, z > 0.
R: Matricea funct ionala
_
_
2x
x
2
+y
2
+z
2
2y
x
2
+y
2
+z
2
2z
x
2
+y
2
+z
2
1
y
+
y
x
2
1+(
x
y
y
x
+z)
2
x
y
2
1
x
1+(
x
y
y
x
+z)
2
1
1+(
x
y
y
x
+z)
2
_
_
are rangul 2.
f (x, y, z) = x +y +z,
g (x, y, z) = x
3
+y
3
+z
3
+ 6xyz,
h(x, y, z) = xy (x +y) +yz (y +z) +zx(z +x) ,
3
si sa se gaseasca relat ia de dependent a funct ional a.
_
_
1 1 1
3x
2
+ 6yz 3y
2
+ 6xz 3z
2
+ 6xy
y
2
+z
2
+ 2x(y +z) z
2
+x
2
+ 2y (z +x) x
2
+y
2
+ 2z (x +y)
_
_
are rangul mai mic decat 3. Relat ia de dependent a funct ionala este: f
3
= g + 3h.
6.38 Daca funct iile f, g, h sunt derivabile si inversabile, atunci funct iile: u = f
_
y
z
_
,
v = g
_
z
x
_
, w = h
_
x
y
_
, denite pe D = R (0, 0, 0), sunt funct ional dependente pe D.
_
_
0
1
z
f

y
z
2
f
z
x
2
g
0
1
x
g
1
y
h

x
y
2
h
0
_
_
are rangul mai mic decat 3.
f (x, y, z) = xy z,
g (x, y, z) = xz +y,
h(x, y, z) =
_
x
2
+ 1
_ _
y
2
+z
2
_
_
x
2
1
_
yz x
_
y
2
z
2
_
,
3
si sa se gaseasca relat ia de dependent a funct ional a.
R: Matricea funct ionala are rangul mai mic decat 3. Relat ia de dependent a funct io-
nala este:
h = f
2
fg +g
2
.
f
1
(x
1
, x
2
, x
3
, x
4
) = x
1
+x
2
x
3
,
f
2
(x
1
, x
2
, x
3
, x
4
) = x
2
1
+x
2
2
+x
2
3
+x
2
4
,
f
3
(x
1
, x
2
, x
3
, x
4
) = 2x
1
x
2
2x
1
x
3
2x
2
x
3
x
2
4
,
4
.
R: Rangul matricei funct ionale este mai mic decat 3. Relat ia de dependent a funct io-
nala este:
f
2
+f
3
= f
2
1
.
f
1
(x
1
, x
2
, . . . , x
n
) = x
1
+x
2
+ +x
n
,
f
2
(x
1
, x
2
, . . . , x
n
) = x
2
1
+x
2
2
+ +x
2
n
,
f
3
(x
1
, x
2
, . . . , x
4
) = x
1
x
2
+x
1
x
3
+ +x
n1
x
n
,
4
.
R: Rangul matricei funct ionale este mai mic decat 3. Relat ia de dependent a funct io-
nala este:
f
2
+ 2f
3
= f
2
1
.
6.5 Schimbari de variabile
6.42 Sa se efectueze schimbarea de variabila independent a x =
1
t
n ecuat ia:
x
2
d
2
y
dx
2
+ 2x
dy
dx
+
a
2
x
2
y = 0.
R: Deoarece:
dt
dx
=
1
x
2
= t
2
si
d
2
t
dx
2
=
2
x
3
= 2t
3
, avem:
dy
dx
=
dy
dt
dt
dx
= t
2
dy
dt
,
d
2
y
dx
2
=
d
2
y
dt
2
_
dt
dx
_
2
+
dy
dt
d
2
t
dx
2
= t
4
d
2
y
dt
2
+ 2t
3
dy
dt
si deci ecuat ia devine:
d
2
y
dt
2
+a
2
y = 0.
6.43 Sa se efectueze schimbarea de variabila independenta indicata n urmatoarele ecu-
at ii pentru funct ia y = y (x):
1) x
2
y
2y = x
2
+
1
x
, x = e
t
.
2) x
3
y
x
2
y
+ 2xy
2y = x
3
+ 3x, x = e
t
.
3)
_
1 +x
2
_
2
y
+ 2x
_
1 +x
2
_
y
+y = 0, x = tg t.
4) (1 +x)
3
y
+ 3 (1 +x)
2
y
+ (1 +x) y = ln (1 +x) , x = e
t
1.
5)
_
1 x
2
_
y
xy
+y = 0, x = cos t.
R: Notam
dy
dt
= y. Se obt ine: 1) y y 2y = e
2t
+e
t
,
2)
...
y
4 y + 5 y 2y = e
3t
+ 3e
t
. 3) y + y = 0. 4) y 2 y +y = te
t
.
5) y + y = 0.
6.44 Sa se efectueze schimbarea variabilei independente n urmatoarele ecuat ii pentru
funct ia y = y (x), luand drept noua variabila independenta funct ia t = t (x) indicata:
1) (1 +x)
2
y
+ (1 +x) y
+y = 4 cos [ln (1 +x)] , t = ln (1 +x) .

2) x
_
1 +x
2
_
y
_
1 x
2
y
1 +x
2
_
y
3x
3
y
2
= 0, t =
1 +x
2
.
R: 1) Notam
dy
dt
= y. Se obt ine: 1) y + y = 4 cos t. 2) y +y y y
2
= 0.
6.45 Funct ia y = y (x) verica ecuat ia
x
2
y
+ 4xy
+
_
2 x
2
_
y = 4x.
Sa se gaseasca ce devine aceasta ecuat ie daca se efectueaza schimbarea de variabila de-
pendent a y =
1
x
2
z, unde z = z (x).
R: z
z = 4x.
6.46 Sa se efectueze schimbarea de variabile independente indicata n urmatoarele ecu-
at ii pentru funct ia z = z (x, y):
1) y
z
x
x
z
y
= 0, u = x, v = x
2
+y
2
.
2) x
z
x
+y
z
y
= z, u = x, v =
x
y
.
3) x
z
x
+
_
1 +y
2
z
y
= xy, u = ln x, v = ln
_
y +
_
1 +y
2
_
.
4) (x +y)
z
x
(x y)
z
y
= 0, u = ln
_
x
2
+y
2
, v = arctg
x
y
.
R: 1)
z
u
= 0. 2) u
z
u
z = 0. 3)
z
u
+
z
v
= e
u
sh v. 4)
z
u

z
v
= 0.
6.47 Sa se efectueze schimbarea de variabile independente x = r cos , y = r sin n
ecuat ia lui Laplace:
2
z
x
2
+

2
z
y
2
= 0.
R: Se obt ine:
2
z
r
2
+
1
r
2
2
z
2
+
1
r
z
r
= 0.
ecuat ia:
y
2
2
z
x
2
2xy

2
z
xy
+x
2
2
z
y
2
x
z
x
y
z
y
= 0.
R: Se obt ine:

2
z
2
= 0.
6.49 Sa se efectueze schimbarea de variabile independente indicata n urmatoarele ecu-
at ii pentru funct ia z = z (x, y):
1) x
2
2
z
x
2
y
2
2
z
y
2
= 0, u = xy, v =
x
y
.
2)

2
z
x
2
a
2
2
z
y
2
= 0, u = ax +y, v = ax +y.
3)

2
z
x
2
4

2
z
xy
+ 3
2
z
y
2
, u = 3x +y, v = x +y.
R: 1)

2
z
uv
=
1
2u
z
v
. 2)

2
z
uv
= 0. 3)

2
z
uv
= 0.
6.50 Sa se efectueze schimbarea de variabile independente u = sin x + x y, v =
x sin x +y, n ecuat ia:
2
z
x
2
+ 2 cos x

2
z
xy
sin
2
x

2
z
y
2
sin x
z
y
= 0.
R:

2
z
uv
= 0.
6.51 Sa se efectueze schimbarea de variabile independente u = x
2
y
2
, v =
y
x
, n
ecuat ia:
xy

2
z
x
2
+
_
x
2
+y
2
_

2
z
xy
+xy

2
z
y
2
y
z
x
x
z
y
= 0.
R: u

2
z
uv

z
v
= 0.
ecuat ia:
dy
dx
=
x +y
x y
.
R: Din
sin dr+r cos d
cos drr sin d
=
cos +sin
cos sin
, se obt ine:
dr
d
= r.
6.53 Sa se efectueze schimbarea de variabile u = x
2
+y
2
, v =
1
x
+
1
y
, w = ln z (x +y),
n ecuat ia:
y
z
x
x
z
y
= (y x) z.
R: Se obt ine:
w
v
= 0.
6.54 Sa se efectueze schimbarea de variabile u = x, v =
1
y
, w =
1
z

1
x
, n ecuat ia:
x
2
z
x
+y
2
z
y
= z
2
.
R: Se obt ine:
w
u
= 0.
6.55 Sa se efectueze schimbarea de variabile u = x +y, v =
x
y
, w =
z
x
, n ecuat ia:
2
z
x
2
2

2
z
xy
+

2
z
y
2
= 0.
R: Se obt ine:

2
w
v
2
= 0.
6.56 Sa se efectueze schimbarea de variabile u = x + y, v = x y, w = xy z, n
ecuat ia:
2
z
x
2
+ 2

2
z
xy
+

2
z
y
2
= 0.
R: Se obt ine:

2
w
u
2
=
1
2
.
Capitolul 7
Extreme pentru funct ii de mai
multe variabile
7.1 Puncte de extrem pentru funct ii de mai multe
variabile
7.1 Sa se determine punctele de extrem ale funct iilor:
1) f(x, y) = x
3
+ 3xy
2
15x 12y. 2) f(x, y) = x
2
+xy +y
2
3x 6y.
3) f(x, y) =
1
2
xy + (47 x y)
_
x
3
+
y
4
_
. 4) f(x, y) = x
3
+y
3
+ 3xy.
R: 1) Punctele stat ionare sunt solut iile sistemului:
f
x
= 3(x
2
+y
2
5) = 0,
f
y
= 6(xy 2) = 0,
adica: (2, 1), (2, 1), (1, 2), (1, 2). Derivatele de ordinul doi sunt:
2
f
x
2
= 6x,

2
f
xy
= 6y,

2
f
y
2
= 6x.
In punctul (2, 1),

1
= 12 > 0,
2
= 108 > 0, (2, 1) este un punct de minim, f(2, 1) =
28.

In punctul (2, 1),
1
= 12 < 0,
2
= 108 > 0, (2, 1) este un punct de
maxim, f(2, 1) = 28.

In punctele (1, 2), (1, 2),
2
= 108 < 0. Nu sunt puncte
de extrem.
2) Un punct stat ionar: (0, 3).
1
= 2 > 0,
2
= 3 > 0. Punctul (0, 3) este un punct
de minim si f
min
= f (0, 3) = 9.
3) Un punct stat ionar: (21, 20).
1
=
2
3
< 0,
2
=
47
144
> 0. Punctul (21, 20) este
un punct de maxim si f
max
= f (21, 20) = 282.
4) Un punct stat ionare: (0, 0), (1, 1). Punctul (0, 0) nu este punct de extrem.
Punctul (1, 1) este un punct de maxim si f
max
= f (1, 1) = 1.
88
CAPITOLUL 7. EXTREME PENTRU FUNCT II DE MAI MULTE VARIABILE 89
7.2 Sa se determine punctele de extrem ale funct iei
f(x, y) = xy +
50
x
+
20
y
, x > 0, y > 0.
R: Punctele stat ionare sunt solut iile sistemului:
f
x
= y
50
x
3
= 0,
f
y
= x
20
y
2
= 0.
Se obt ine un singur punct stat ionar (5, 2). Derivatele de ordinul doi sunt:
2
f
x
2
=
100
x
3
,

2
f
xy
= 1,

2
f
y
2
=
40
y
3
.
Deci
1
=
4
5
> 0,
2
= 3 > 0. Punctul (5, 2) este un punct de minim si
f
min
= f (5, 2) = 30.
7.3 Sa se gaseasca extremele funct iilor:
1) z = (x 1)
2
+ 2y
2
. 2) z = x
2
+xy +y
2
2x y.
3) z = (x 1)
2
2y
2
. 4) z = x
3
y
2
(6 x y) , x > 0, y > 0.
5) z = xy
_
1
x
2
3

y
2
3
. 6) z = x
4
+y
4
2x
2
+ 4xy 2y
2
.
7) z = 1
_
x
2
+y
2
_
2/3
. 8) z =
_
x
2
+y
2
_
e
(x
2
+y
2
)
.
R: 1) z
min
= z (1, 0) = 0. 2) z
min
= z (1, 0) = 1 3) Nu are extreme.
4) z
max
= z (3, 2) = 108.
5) Puncte stat ionare: (0, 0),
_
0,
3
_
,
_
3, 0
_
, (1, 1), (1, 1), (1, 1), (1, 1).
Extreme: z
max
= z (1, 1) = z (1, 1) =
1
3
3, z
min
= z (1, 1) = z (1, 1) =
1
3
3.
6) z
min
= z
_
2,
2
_
= z
_
2,
2
_
= 8. 7) z
max
= z (0, 0) = 1.
8) z
min
= z (0, 0) = 0.

In punctele cercului x
2
+y
2
= 1, z
max
=
1
e
.
1) z =
1+x+y
1+x
2
+y
2
2) z =
_
x
2
+y
2
_
e
2x+3y
, x 0, y 0.
3) z = x
3
+y
3
9xy + 27. 4) z = sin x + sin y + cos (x +y) , x, y
_
0,

2
.
5) z = x
4
+y
4
+ 2x
2
y
2
8x + 8y.
R: 1) z
max
= z (1, 1) =
3. 2) z
min
= z (0, 0) = 0.
3) (0, 0) nu este punct de extrem, z
min
= z (3, 3) = 0.
4)
_
2
,

2
_
nu este punct de extrem, z
max
= z
_
6
,

6
_
=
3
2
.
5) z
min
= z (1, 1) = 12.
1) f (x, y, z) = x
2
+y
2
+z
2
+ 2x + 4y 6z.
2) f (x, y, z) = x
3
+y
2
+z
2
+ 12xy + 2z.
3) f (x, y, z) = sin x + sin y + sin z sin (x +y +z) , x, y, z (0, ) .
R: 1) Un punct stat ionar: (1, 2, 3). d
2
f (1, 2, 3) = 2
_
dx
2
+dy
2
+dz
2
_
este
o forma patratica pozitiv denita si deci punctul (1, 2, 3) este un punct de minim,
f
min
= f (1, 2, 3) = 14.
2) Doua puncte stat ionare: (0, 0, 1), (24, 144, 1).

Insa
d
2
f (x, y, z) = 6xdx
2
+ 2 dy
2
+ 2 dz
2
+ 24 dxdy,
iar: d
2
f (0, 0, 1) = 2 dy
2
+ 2 dz
2
+ 24 dxdy = 2 (dy + 6 dx)
2
72 dx
2
+ 2 dz
2
, forma
patratica nedenita, deci (0, 0, 1) nu este punct de extrem,
d
2
f (24, 144, 1) = 144 dx
2
+ 2 dy
2
+ 2 dz
2
+ 24 dxdy = (12 dx +dy)
2
+dx
2
+ 2dz
2
,
forma patratica pozitiv denita si deci punctul (24, 144, 1) este un punct de minim,
f
min
= f (24, 144, 1) = 6913.
3) f
max
= f
_
2
,

2
,

2
_
= 4.
7.2 Extreme pentru funct ii denite implicit
7.6 Sa se gaseasca extremele urmatoarelor funct ii z = f (x, y), denite implicit prin
ecuat iile:
1) F (x, y; z) = x
2
+y
2
+z
2
2x + 4y 6z 11 = 0.
2) F (x, y; z) = x
3
y
2
+z
2
3x + 4y +z 8 = 0.
R: 1) Sistemul:
F
x
= 2x 2 = 0, F
y
= 2y + 4 = 0, F = x
2
+y
2
+z
2
2x + 4y 6z 11 = 0,
are solut iile: (1, 2; 2) si (1, 2; 8). Ecuat ia F (x, y; z) = 0 deneste doua funct ii:
z = z
1
(x, y) si z = z
2
(x, y).
Pentru z = z
1
(x, y):
A
11
=
F
xx
(1, 2; 2)
F
z
(1, 2; 2)
=
1
5
, A
12
=
F
xy
(1, 2; 2)
F
z
(1, 2; 2)
= 0,
A
22
=
F
yy
(1, 2; 2)
F
z
(1, 2; 2)
=
1
5
si deci
1
=
1
5
> 0,
2
=
1
25
> 0, deci (1, 2) este un punct de minim, z
min
=
z
1
(1, 2) = 2.
Pentru z = z
2
(x, y):
A
11
=
F
xx
(1, 2; 8)
F
z
(1, 2; 8)
=
1
5
, A
12
=
F
xy
(1, 2; 8)
F
z
(1, 2; 8)
= 0, A
22
=
F
yy
(1, 2; 8)
F
z
(1, 2; 8)
=
1
5
si deci
1
=
1
5
< 0,
2
=
1
25
> 0, deci (1, 2) este un punct de maxim, z
max
=
z
2
(1, 2) = 8.
2) Sistemul:
F
x
= 3x
2
3 = 0, F
y
= 2y + 4 = 0, F = x
3
y
2
+z
2
3x + 4y +z 8 = 0,
are solut iile: (1, 2; 2), (1, 2; 1), (1, 2; 3), (1, 2; 2). Ecuat ia F (x, y; z) = 0 deneste
doua funct ii: z = z
1
(x, y) si z = z
2
(x, y), ecare avand cate doua puncte stat ionare.
Pentru z = z
1
(x, y), n primul punct:
A
11
=
F
xx
(1, 2; 2)
F
z
(1, 2; 2)
=
6
5
, A
12
=
F
xy
(1, 2; 2)
F
z
(1, 2; 2)
= 0, A
22
=
F
yy
(1, 2; 2)
F
z
(1, 2; 2)
=
2
5
si deci
1
=
6
5
< 0,
2
=
12
25
< 0, deci (1, 2) nu este un punct de de extrem.

In
punctul al doilea:
A
11
=
F
xx
(1, 2; 1)
F
z
(1, 2; 1)
= 2, A
12
=
F
xy
(1, 2; 1)
F
z
(1, 2; 1)
= 0, A
22
=
F
yy
(1, 2; 1)
F
z
(1, 2; 1)
=
2
3
.
Deci
1
= 2 > 0,
2
=
4
3
min
= z
1
(1, 2) = 1.
Pentru z = z
2
(x, y), n primul punct:
A
11
=
F
xx
(1, 2; 3)
F
z
(1, 2; 3)
=
6
5
, A
12
=
F
xy
(1, 2; 3)
F
z
(1, 2; 3)
= 0, A
22
=
F
yy
(1, 2; 3)
F
z
(1, 2; 3)
=
2
5
si deci
1
=
6
5
> 0,
2
=
12
25
< 0, deci (1, 2) nu este un punct de extrem.

In punctul
al doilea:
A
11
=
F
xx
(1, 2; 2)
F
z
(1, 2; 2)
= 2, A
12
=
F
xy
(1, 2; 2)
F
z
(1, 2; 2)
= 0,
A
22
=
F
yy
(1, 2; 2)
F
z
(1, 2; 2)
=
2
3
si deci
1
= 2 < 0,
2
=
4
3
max
=
z
1
(1, 2) = 2.
ecuat iile:
1) F (x, y; z) =
x
2
12
+
y
2
4
+
z
2
3
1 = 0.
2) F (x, y; z) =
x
2
3
+
y
2
4

z
2
25
+ 1 = 0.
R: 1) Sistemul F
x
= 0, F
y
= 0, F = 0, are solut iile
_
0, 0;
3
_
,
_
0, 0;
3
_
.
Ecuat ia F (x, y; z) = 0 deneste doua funct ii: z = z
1
(x, y) si z = z
2
(x, y), z
min
=
z
1
(0, 0) =
3, z
max
= z
2
(0, 0) =
3.
2) Sistemul F
x
= 0, F
y
= 0, F = 0, are solut iile (0, 0; 5), (0, 0; 5).
Ecuat ia F (x, y; z) = 0 deneste doua funct ii: z = z
1
(x, y) si z = z
2
(x, y), z
min
=
z
1
(0, 0) = 5, z
max
= z
2
(0, 0) = 5.
ecuat iile:
1) F (x, y; z) = 4xy z
2
4x 4y + 8 = 0.
2) F (x, y; z) = 5x
2
+ 6y
2
+ 7z
2
4xy + 4yz 10x + 8y + 14z 6 = 0.
R: 1) Sistemul F
x
= 0, F
y
= 0, F = 0, are solut iile (0, 0; 2), (0, 0; 2).
7.3 Extreme condit ionate
7.9 Sa se gaseasca extremele condit ionate ale urmatoarelor funct ii:
1) z = xy, pentru x +y 1 = 0. 2) z = x + 2y, pentru x
2
+y
2
5 = 0.
3) z = x
2
+y
2
, pentru
x
2
+
y
3
= 1. 4) z = cos
2
x + cos
2
y, pentru y x =

4
.
5) z = x
2
+y
2
, pentru
x
a
+
y
b
= 1. 6) z =
1
x
+
1
y
, pentru
1
x
2
+
1
y
2
=
1
a
2
.
R: 1) Construim funct ia lui Lagrange: L(x, y; ) = xy +(x +y 1). Sistemul:
L
x
= y + = 0, L
y
= x + = 0, L
= x +y 1 = 0
are solut ia: x
0
=
1
2
, y
0
=
1
2
,
0
=
1
2
. Fie (x, y) = L(x, y;
1
2
) = xy
1
2
(x +y 1).
Atunci
d
2
_
1
2
,
1
2
_
= dxdy.
Insa dx +dy = 0 si deci d

2
_
1
2
,
1
2
_
= dx
2
< 0. z
max
= z
_
1
2
,
1
2
_
=
1
4
.
2) z
max
= z (1, 2) = 5, z
min
= z (1, 2) = 5.
3) z
min
= z
_
18
13
,
12
13
_
=
36
13
.
4) z
max
= z
_
7
8
+k,
9
8
+k
_
=
2+
2
2
,
z
min
= z
_
3
8
+k,
5
8
+k
_
=
2
2
2
.
5) z
min
= z
_
ab
2
a
2
+b
2
,
a
2
b
a
2
+b
2
_
=
a
2
b
2
a
2
+b
2
.
6) z
max
= z
_
a
2, a
2
_
= 4a
2
, z
min
= z
_
a
2, a
2
_
= 4a
2
.
1) z = xy, pentru 2x + 3y 5 = 0.
2) z = x
2
+y
2
, pentru
_
x
2
_
2
+
_
y
2
_
2
= 9.
3) z = 6 4x 3y, pentru x
2
+y
2
= 1.
4) z = cos
2
x + cos
2
y, pentru x y =

4
, x, y
_
0,

4
_
.
R: Avem:
1) L(x, y; ) = xy +(2x + 3y 5), =
5
3
, z
max
= z
_
5
4
,
5
6
_
=
25
24
.
2)
1
=
5
3
, z
max
= z
_
5
2
2
,
5
2
2
_
= 25,
2
=
1
3
,
z
min
= z
_
2
2
,
2
2
_
= 1.
3)
1
=
5
2
, z
max
= z
_
4
5
,
3
5
_
= 11,
2
=
5
2
, z
min
= z
_
4
5
,
3
5
_
= 1.
4) z
max
= z
_
3
8
,

8
_
= 1.
1) u = x 2y + 2z, pentru x
2
+y
2
+z
2
= 9.
2) u = x
2
+y
2
+z
2
, pentru
x
2
a
2
+
y
2
b
2
+
z
2
c
2
= 1, a > b > c.
3) u = xy
2
z
3
, pentru x + 2y + 3z = 6, x > 0, y > 0, z > 0.
4) u = xy +xz +yz, pentru xyz = 1, x > 0, y > 0, z > 0.
5) u = x +y +z, pentru
1
x
+
1
y
+
1
z
= 1, x > 0, y > 0, z > 0.
R: Avem:
1) u
min
= u(1, 2, 2) = 9, u
max
= u(1, 2, 2) = 9.
2) u
max
= u(a, 0, 0) = a, u
min
= u(0, 0, c) = c. 3) u
max
= u(1, 1, 1) = 1.
4) u
min
= u(1, 1, 1) = 3. 5) u
min
= u(3, 3, 3) = 9.
1) u = xyz, pentru x +y +z = 5, xy +xz +yz = 8, x y z > 0.
2) u = xyz, pentru x +y +z = 0, x
2
+y
2
+z
2
= 1.
R: 1) Funct ia lui Lagrange:
L(x, y, z; , ) = xyz +(x +y +z 5) +(xy +xz +yz 8) ,
are punctele stat ionare:
_
7
3
,
4
3
,
4
3
;
16
9
,
4
3
_
si (2, 2, 1; 4, 2).
u
max
= u
_
7
3
,
4
3
,
4
3
_
=
112
27
, u
min
= u(2, 2, 1) = 4.
2) u
min
=
1
3
6
, u
max
=
1
3
6
.
1) u = x
4
+y
4
+z
4
, pentru x +y +z = 3.
2) u = x
3
+y
3
+z
3
, pentru x
2
+y
2
+z
2
= 3, x > 0, y > 0, z > 0.
7.14 Sa se determine dimensiunile unui paralelipiped dreptunghic a..:
1) Aria totala sa e egala cu 2a
2
si volumul maxim.
2) Suma celor trei dimensiuni egala cu a si aria totala maxima.
3) Volumul egal cu a
3
si aria totala minima.
R: Avem:
1) 1
max
= 1
_
a
3
,
a
3
,
a
3
_
=
a
3
3
9
.
2) /
max
= /
_
a
3
,
a
3
,
a
3
_
=
2
3
a
2
.
3) /
min
= /(a, a, a) = 6a
2
.
Capitolul 8
Siruri si serii de funct ii
8.1 Siruri de funct ii reale
8.1 Se da sirul de funct ii (f
n
), f
n
(x) =
_
n
2
e
nx
2
2
. Sa se determine mult imea de
convergent a si funct ia limita.
R: Deoarece:
lim
n
f
n
(x) =
_
0, x R 0 ,
, x = 0,
rezulta ca mult imea de convergent a este A = R 0, iar funct ia limita: f (x) = 0.
8.2 Sa se arate ca sirul de funct ii f
n
(x) =
x
2
n+1
, x R, este simplu convergent pe R
catre f(x) = 0.
R:

Intr-adevar,
x
2
n+1
< d.d. n >
x
2
. Deci
N(, x) =
_ _
x
2
_
, < x
2
,
0, x
2
.
n
(x) =
cos nx
n
2
+1
, x [0, ], este uniform convergent
catre f(x) = 0.
R:

Intr-adevar,
cos nx
n
2
+1
< daca
1
n
2
+1
< , adica d.d. n
2
>
1
. Deci
N() =
_ _
1
, < 1,
0, 1.
n
(x) =
sin nx
n
, x R cu > 0, este uniform

convergent pe R catre f(x) = 0.
R:

Intr-adevar,

sin nx
n
1
n
0.
94
CAPITOLUL 8. SIRURI SI SERII DE FUNCT II 95
n
(x) =
1
ne
nx
, x [0, ), este uniform convergent
pe [0, ) catre f(x) = 0.
R: Pentru x 0, e
nx
1 si deci 0 < f
n
(x) <
1
n
0.
8.6 Se da sirul de funct ii f
n
(x) =
x
2
n
2
+x
4
, x [1, ). Sa se calculeze lim
n
f
n
(x) =
f (x). Sa se arate ca sirul de funct ii (f
n
) este uniform convergent pe [1, ) catre f.
R: 0 < f
n
(x) =
2nx
2
n
2
+x
4

1
2n
<
1
2n
0.
n
(x) =
x
n+x
, x (0, ). Sa se calculeze lim
n
f
n
(x) =
f (x). Sa se arate ca sirul de funct ii (f
n
) nu este uniform convergent pe (0, ) catre f.
R: f (x) = 0, nsa pentru x
n
= n, f
n
(x
n
) =
1
2
.
n
(x) =
x
n+x
, x [3, 4]. Sa se arate ca sirul de funct ii (f
n
)
este uniform convergent pe [3, 4] catre funct ia f (x) = 0, x [3, 4].
R: Pentru 3 x 4, avem: 0 < f
n
(x)
4
n+3
<
4
n
0.
8.9 Sa se arate ca sirul de funct ii (f
n
), f
n
(x) =
x
3
x
3
+n
3
, nu este uniform convergent pe
(0, ).
R: f (x) = 0, nsa pentru x
n
= n, f
n
(x
n
) =
1
2
.
n
), f
n
: R R, denite prin: f
n
(x) =
n
n=0
x
k
. Sa se
arate ca mult imea de convergent a a sirului este A = (1, 1), nsa sirul nu este uniform
convergent pe (1, 1). Sa se gaseasc a o mult ime de convergent a uniforma.
R:Deoarece, f
n
(x) =
1
1x
+
x
n+1
x1
, pentru x ,= 1, rezulta ca f
n
(x) este divergent
pentru [x[ > 1, este convergent pentru [x[ < 1. Apoi, f
n
(1) = n + 1 , f
n
(1) =
1
2
(1 + (1)
n
) este un sir divergent. Deci mult imea de convergent a a sirului este A =
(1, 1) si funct ia limita este f (x) =
1
1x
.
Daca sirul ar uniform convergent pe (1, 1), pentru orice > 0 ar exista un N ()
a..
x
n+1
x1
< pentru orice n > N () si orice x (1, 1), inegalitate echivalenta cu:
n + 1 >
1
ln
1
|x|
_
ln
1
ln [x 1[
_
, dar sup
|x|<1
_
ln
1
ln
1
|x|
+
ln
1
|x1|
ln
1
|x|
_
= +.
Pentru orice interval [a, a] (1, 1), putem lua
N () =
_
ln
1
ln
1
|a|
_
si deci sirul (f
n
) este uniform convergent pe orice interval [a, a] (1, 1).
n
), f
n
: R R, denite prin: f
n
(x) = 1 +x
2n
.
1) Sa se gaseasc a mult imea de convergent a a sirului si funct ia limita.
2) Sa se arate ca sirul nu este uniform convergent pe (1, 1).
3) Sa se gaseasc a o mult ime de convergent a uniforma.
R: 1) A = [1, 1], iar funct ia limita este:
f (x) =
_
1, x (1, 1) ,
2, x 1, 1 .
3) Sirul (f
n
) este uniform convergent pe orice interval [a, a] (1, 1).
n
), f
n
: R R, denite prin:
f
n
(x) =
n
k=1
sinkx
k
3
,
este uniform convergent pe R, iar limita sa este o funct ie continua cu derivata continua
pe R.
R: Aplicam criteriul lui Cauchy:
[f
n+p
(x) f
n
(x)[
p
k=1
1
(n +k)
3
<
p
k=1
1
(n +k)
2
<
p
k=1
1
(n +k 1) (n +k)
<
1
n
.
Analog se arata ca sirul (f
n
), f
n
(x) =
n
k=1
cos kx
k
2
, este uniform convergent pe R. Deci
f
(x) = lim
n
n
k=1
cos kx
k
2
.
n
), denite prin f
n
(x) =xarctg (nx), este uniform
convergent pe [0, ).
R: Aplicam criteriul lui Cauchy:
[f
n+p
(x) f
n
(x)[ = x [arctg ((n +p) x) arctg (nx)[ = x arctg
px
1 + (n +p) nx
2
<
< x arctg
px
(n +p) nx
2
x
p
(n +p) nx
=
p
(n +p) n
<
1
n
.
n
), denite prin f
n
(x) =
sin nx
n
2
, converge uniform
pe R catre funct ia f(x) = 0.
R: Se va observa ca

sin nx
n
2
1
n
2
.
n
), denite prin f
n
(x) =
sin
2
nx
n+1
, x [0, ], este
uniform convergent catre funct ia f(x) = 0 si ca desi funct iile f
n
si f sunt derivabile pe
[0, ], sirul derivatelor f
n
(x) =
n
n+1
sin 2nx nu este convergent pe [0, ].
R:

Intr-adevar, pentru x =

4
sirul f
n
_
4
_
este divergent.
n
), f
n
(x) =
x
1+n
2
x
2
, x [1, 1]. Sa se cerceteze daca se
poate aplica sirului (f
n
) teorema de derivare termen cu termen.
R: Sirul este convergent pe [1, 1] la funct ia f (x) = 0. Sirul derivatelor:
f
n
(x) =
1 n
2
x
2
(1 +n
2
x
2
)
2
, are lim
n
f
n
(x) =
_
1, x = 0,
0, x [1, 1] 0
si nu este uniform convergent pe [1, 1]. Deci nu se poate aplica sirului (f
n
) teorema de
derivare termen cu termen.
8.17 Se da sirul (f
n
), f
n
(x) =
1
n
arctg x
n
, x R. Sa se arate ca:
_
lim
n
f
n
(x)
_
x=1
,= lim
n
f
n
(1) .
R: Deoarece mult imea valorilor funct iei arctg x este intervalul
_
2
,

2
_
, rezulta ca
[arctg x[ <

2
si deci:
0 [f
n
(x)[ =
1
n
arctg x
n
<
1
n

2
,
de unde deducem ca sirul este convergent pe R la funct ia f (x) = 0 si deci: f
(1) = 0.
Pe de alta parte:
lim
n
f
n
(1) = lim
n
_
x
n1
1 +x
2n
_
x=1
=
1
2
.
n
), f
n
: [0, 1] R, denite prin: f
n
(x) = nxe
nx
2
este convergent, nsa
lim
n
_
1
0
f
n
(x) dx ,=
_
1
0
lim
n
f
n
(x) dx.
R:

Intr-adevar,
lim
n
_
1
0
f
n
(x) dx = lim
n
_
1
2

1
2e
n
_
=
1
2
,
_
1
0
lim
n
f
n
(x) dx = 0.
n
), f
n
n
(x) =
n
2
x
3
e
n
2
x
3
este convergent, nsa
lim
n
_
1
0
f
n
(x) dx ,=
_
1
0
lim
n
f
n
(x) dx.
R:

Intr-adevar,
lim
n
_
1
0
f
n
(x) dx = lim
n
_
1
3

1
3e
n
2
_
=
1
3
,
_
1
0
lim
n
f
n
(x) dx = 0.
n
), f
n
n
(x) =
nx(1 x)
n
nu este uniform convergent pe [0, 1], totusi
lim
n
_
1
0
f
n
(x) dx =
_
1
0
lim
n
f
n
(x) dx.
R: Sirul este convergent pe [0, 1] la funct ia f (x) = 0. Dar, pentru x
n
=
1
n
0,
f
n
(x
n
) =
_
1
1
n
_
n
1
e
,= 0,
deci convergent a nu este uniforma. Pe de alta parte:
_
1
0
f
n
(x) dx = n
_
1
0
x(1 x)
n
dx =
n
(n + 1) (n + 2)
0,
_
1
0
lim
n
f
n
(x) dx = 0.
8.2 Serii de funct ii
8.21 Sa se determine mult imea de convergent a a urmatoarelor serii de funct ii:
1)
n=1
_
n + 1
n
_
n
_
1 x
1 2x
_
n
. 2)
n=1
sin
n
x
n
, R. 3)
n=2
(1)
n
ln n
_
1 x
2
1 +x
2
_
n
.
R: 1) Aplicam criteriul radacinii: A = (, 0)
_
2
3
, +
_
. 2) Aplicam criteriul
radacinii: A = R
_
2
+ 2k
_
, R. Pentru x =

2
+ 2k, obt inem seria armonica
generalizata, convergenta daca > 1, iar pentru x =
2
+2k, obt inem seria armonica
generalizata alternanta, convergenta daca > 0. 3) Aplicand criteriul raportului obt inem
o serie convergenta pentru: x R0. Pentru x = 0 seria este de asemenea convergenta.
Deci A = R.
1)
n=1
(1)
n
n + 1
n
2
+n + 1
_
x
2
2
1 2x
2
_
n
. 2)
n=1
n + 1
(n
3
+n + 1)
1
ln (n
2
+ 1)

_
x
3
2x
_
n
,
R.
R: 1) Din
x
2
2
12x
2
< 1 rezulta x (, 1) (1, +). Pentru x = 1 seria este

convergenta, conform criteriului lui Leibniz. Deci: A = (, 1] [1, +). 2) Din
x
3
2x
< 1 rezulta ca seria este convergenta pentru orice R pentru:

x
_
1 +
5
2
, 1
_
_
1
5
2
,
1 +
5
2
_
_
1,
1 +
5
2
_
.
Pentru x
_
1+
5
2
,
1+
5
2
, 1
_
seria este convergenta daca
1
6
, iar pentru x
_
1,
1
5
2
,
1+
5
2
_
seria este convergenta daca >
1
2
.
1)
n=1
(1)
n
1
3
n
n
2
+ 1
tg
n
x. 2)
n=0
(1)
n
n
2
+ 1
n
2
+n + 1
_
4x 1
x + 3
_
n
.
R: 1) A =
_
3
,

3
. 2)
_
2
5
,
4
3
.
8.24 Sa se studieze convergent a urmatoarelor serii de funct ii, pe mult imile indicate:
1)
n=1
sinnx
n
, x [, 2 ] , (0, ) . 2)
n=1
cos
2n
3
x
2
+n
, x R.
R: Din criteriul lui Dirichlet rezulta ca seriile sunt uniform convergente pe mult imile
indicate.
8.25 Sa se studieze convergent a urmatoarelor serii de funct ii, denite pe R:
1)
n=1
(1)
n
x
2
1 +n
3
x
4
, 2)
n=1
arctg
2x
x
2
+n
4
. 3)
n=1
_
e
_
1 +
1
n
_
n
_
cos nx
n + 1
.
R: 1) Din
_
1 x
2
n
3
_
2
0 pentru orice x R, deducem ca [f
n
(x)[
1
2
n
3
,
x R si n N
.

In baza criteriului lui Weierstrass, rezulta ca seria este absolut si
uniform convergenta pe R. 2) Deoarece [f
n
(x)[ arctg
1
n
2
, x R si n N
.

In baza
criteriului lui Weierstrass, rezulta ca seria este absolut si uniform convergenta pe R. 3)
Deoarece [f
n
(x)[ <
3
n
2
, x R si n N
.

In baza criteriului lui Weierstrass, rezulta
ca seria este absolut si uniform convergenta pe R.
8.26 Sa se studieze convergent a simpla si uniforma a urmatoarelor serii de funct ii, pe
mult imile indicate:
1) x +
n=1
_
x
1 +nx

x
1 + (n 1) x
_
, x [0, 1] . 2) 1 +
n=1
_
x
n
x
n1
_
, x
_
0,
1
2
_
.
R: 1) s
n
(x) =
x
1+nx
0, deci seria este convergenta la funct ia f (x) = 0 pe [0, 1].
Apoi, din: [s
n
(x) 0[ <
1
n
, x [0, 1], rezulta ca seria este uniform convergenta pe
[0, 1].
2) s
n
(x) = x
n
0 si [s
n
(x) 0[ [x[
n
_
1
2
_
n
, rezulta ca seria este uniform
convergenta pe
_
0,
1
2
.
8.27 Sa se arate ca seria de funct ii:
n=1
_
nx
1 +n
2
x
2

(n 1) x
1 + (n 1)
2
x
2
_
,
este convergenta pe [0, 1] la o funct ie continua, dar nu este uniform convergenta pe [0, 1].
R: 1) Sirul: s
n
(x) =
nx
1+n
2
x
2
converge la funct ia f (x) = 0 pe [0, 1] care este continua.
Pe de alta parte, oricare ar n N, pentru x
n
=
1
n
, avem: [s
n
(x) 0[ =
1
2
. Asadar,
exista un > 0 a.. oricare ar n N, [s
n
(x) 0[ pentru cel put in un punct din
intervalul [0, 1]. Deci seria nu este uniform convergenta pe [0, 1].
8.28 Sa se studieze convergent a simpla si uniforma a urmatoarelor serii de funct ii, pe
mult imile indicate:
1)
n=1
_
nx
1+n+x

(n1)x
n+x
_
, x [0, 1].
2)
n=1
_
nx
1+nx

(n1)x
(n)1+x
_
, x [0, 1].
3)
n=1
_
nxe
nx
(n 1) xe
(n1)x
, x [0, 1].
4)
n=1
(1)
n+1
x
2
(1+x)
n , x R.
5)
n=1
_
x
n
x
2n
x
n1
+x
2n2
_
, x [0, 1].
6)
n=1
(1)
n+1
x
2
+n
, x R.
R: 1) Uniform convergenta. 2) Simplu convergenta. 3) Simplu convergenta. 4) Con-
form criteriului lui Cauchy, seria este uniform convergenta pe R. 5) Simplu convergenta.
6) Uniform convergenta.
8.29 Sa se arate ca seriile urmatoare sunt uniform convergente pe mult imile indicate:
1)
n=1
x
n
n
2
, x [1, 1] . 2)
n=1
sin nx
2
n
, x R. 3)
n=1
(1)
n1
x
n
n
, x [0, 1] .
R: 1) Din [x[ 1, rezulta

x
n
n
2
1
n
2
.
2)

sin nx
2
n
1
2
n
, pe R.
3)
(1)
n1
x
n
n
, pe [0, 1].
8.30 Aplicand derivarea si integrarea termen cu termen sa se gaseasca sumele urma-
toarelor serii de funct ii denite pe intervalul (1, 1):
1)
n=1
nx
n1
. 2)
n=1
1
n
x
n
. 3)
n=1
(1)
n1
n
x
n
. 4)
n=0
(1)
n
2n + 1
x
2n+1
. 5)
n=1
n
2
x
n1
.
R: Seria de funct ii
n=0
x
n
este convergenta pe intervalul marginit (1, 1) si are ca
suma funct ia f (x) =
1
1x
.
1) Derivand termen cu termen seria
n=0
x
n
obt inem
n=1
nx
n1
=
1
(1x)
2
.
2) Integrand termen cu termen seria
n=0
x
n
obt inem
n=1
1
n
x
n
= ln (1 x).
3) Trecand pe x n x n 2) obt inem
n=1
(1)
n1
n
x
n
= ln (1 x).
4) Trecand x n x
2
n seria
n=0
x
n
obt inem convergenta
n=0
(1)
n
x
2n
a carei suma
este
1
1+x
2
. Integrand termen cu termen aceasta serie, obt inem
n=0
(1)
n
2n + 1
x
2n+1
= arctg x.
5)
n=0
n
2
x
n1
=
x(1+x)
(1x)
3
.
_
1
0
_

n=1
_
x
n
x
2n
x
n1
+x
2n2
_
_
dx =
n=1
_
1
0
_
x
n
x
2n
x
n1
+x
2n2
_
dx.
R: Seria
n=1
n=1
_
x
n
x
2n
x
n1
+x
2n2
_
are ca suma funct ia f (x) = 0, deci
_
1
0
f (x) dx = 0. Pe de alta parte:
n=1
_
1
0
_
x
n
x
2n
x
n1
+x
2n2
_
dx =
n=1
_
1
n + 1

1
n
+
1
2n 1

1
2n + 1
_
= 0.
8.3 Serii de puteri
8.32 Sa se calculeze raza de convergent a a urmatoarelor serii de puteri:
1)
n=1
n
2
n
x
n
. 2)
n=1
n
(x 1)
n
. 3)
n=1
(2n)!
(n!)
2
(x + 3)
n
.
R: 1) = lim
n
n
_
[a
n
[ = lim
n
n
_
n
2
n
=
1
2
, deci r = 2. 2) = lim
n
n
_
[a
n
[ =
lim
n
n
= 1, deci r = 1. 3) = lim
n
a
n+1
a
n
= 4, deci r =
1
4
.
8.33 Sa se determine intervalul de convergent a si sa se studieze convergent a la capetele
intervalului, pentru urmatoarele serii de puteri:
1)
n=0
x
n
(n + 1) 3
n
. 2)
n=0
(1)
n
x
n
5
n
n + 1
. 3)
n=0
2
n
(x + 2)
n
(2n + 1)
2
3
n
. 4)
n=1
(x 1)
n
(2n 1) 2
n
.
R: 1) [3, 3). 2) (5, 5]. 3)
_
2
3
2
, 2 +
3
2
_
. 4) [1, 3).
8.34 Sa se determine intervalul de convergent a si sa se studieze convergent a la capetele
intervalului, pentru urmatoarele serii de puteri:
1)
n=2
(1)
n
n
2
+ 1
n ln
n
x
n
, > 1. 2)
n=1
1 5 9 (4n 3)
n!
x
n
.
R: 1) r = 1.

In punctul x = 1 seria este convergenta, conform criteriului lui Leibniz.
In punctul x = 1 seria este convergenta, conform criteriului lui Bertrand. Deci intervalul
de convergent a este [1, 1].
2) r =
1
4
.

In punctul x =
1
4
seria este divergenta, conform criteriului lui Raabe-
Duhamel, iar n punctul x =
1
4
seria este convergenta, conform criteriului lui Leibniz.
Deci intervalul de convergent a este
_
1
4
,
1
4
_
.
8.4 Serii Taylor
1) e
x
= 1 +
1
1!
x +
1
2!
x
2
+ +
1
n!
x
n
+ , x R.
2) sin x =
1
1!
x
1
3!
x
3
+
1
5!
x
5
+ (1)
n1
1
(2n1)!
x
2n1
+ , x R.
3) cos x = 1
1
2!
x
2
+
1
4!
x
4
+ (1)
n
1
(2n)!
x
2n
+ , x R.
4) ln (1 +x) = x
1
2
x
2
+
1
3
x
3
+ (1)
n1
1
n
x
n
+ , x (1, 1].
8.36 Sa se arate ca pentru orice R si x (1, 1) are loc dezvoltarea binomiala:
(1 +x)
= 1 +

1!
x +
( 1)
2!
x
2
+ +
( 1) ( n + 1)
n!
x
n
+ .
8.37 Sa se stabileasca formula lui Euler: e
ix
= cos x +i sin x, x R.
8.38 Sa se gaseasca seriile Mac-Laurin ale funct iilor:
1) ch x =
e
x
+e
x
2
,
2) sh x =
e
x
e
x
2
.
R: Se obt ine:
1) ch x = 1 +
1
2!
x
2
+
1
4!
x
4
+ +
1
(2n)!
x
2n
+ , x R.
2) sh x =
1
1!
x +
1
3!
x
3
+
1
5!
x
5
+ +
1
(2n + 1)!
x
2n+1
+ , x R.
8.39 Sa se gaseasca seriile Mac-Maurin ale urmatoarelor funct ii:
1) f (x) =
3
(1x)(1+2x)
. 2) f (x) = a
x
, a > 0.
3) f (x) = cos (x +) . 4) f (x) = sin
2
x.
5) f (x) = ln (2 +x) .
R: 1) Putem scrie:
f (x) =
1
1 x
+
2
1 + 2x
=
n=0
_
1 + (1)
n
2
n+1
x
n
, [x[ <
1
2
.
2) Se obt ine:
f (x) = 1 +
n=0
ln
n
a
n!
x
n
, x R.
3) Set ine seama ca: f (x) = cos xcos sin xsin . 4) Set ine seama ca: f (x) =
1
2
(1 cos x). 5) Funct ia se mai poate scrie: f (x) = ln 2 +ln
_
1 +
x
2
_
, pentru x (2, 2].
8.40 Aplicand derivarea si integrarea termen cu termen, sa se gaseasca seriile Mac-
Laurin ale urmatoarelor funct ii:
1) f (x) = (1 +x) ln (1 +x) . 2) f (x) = arctg x.
3) f (x) = arcsin x. 4) f (x) = ln
_
x +
1 +x
2
_
.
R: 1) Deoarece f
(x) = ln (1 +x), t inand seama de dezvoltarea funct iei ln (1 +x),

prin integrare obt inem:
(1 +x) ln (1 +x) =
1
1 2
x
2
1
2 3
x
3
+ + (1)
n
1
n(n 1)
x
n
+ , x (1, 1].
2) Avem ca: f
(x) =
1
1+x
2
=
_
1 +x
2
_
1
. Dar, nlocuind n dezvoltarea binomiala,
pentru = 1, pe x prin x
2
, obt inem:
f
(x) =
n=0
(1)
n
x
2n
,
care prin integrare, da:
arctg x =
n=0
(1)
n
1
2n + 1
x
2n+1
, x (1, 1) .
3) Avem ca: f
(x) =
1
1x
2
=
_
1 x
2
_
1/2
. Dar, nlocuindn dezvoltarea binomiala,
pentru =
1
2
, pe x prin x
2
, obt inem:
f
(x) = 1 +
n=1
(2n 1)!!
(2n)!!
x
2n
,
arcsin x = x +
n=1
(2n 1)!!
(2n)!!
1
2n + 1
x
2n+1
, x (1, 1) .
4) Avem ca: f
(x) =
1
1+x
2
=
_
1 +x
2
_
1/2
. Dar, nlocuindn dezvoltarea binomiala,
pentru =
1
2
, pe x prin x
2
, obt inem:
f
(x) = 1 +
n=1
(1)
n
(2n 1)!!
(2n)!!
x
2n
,
ln
_
x +
_
1 +x
2
_
= x +
n=1
(1)
n
(2n 1)!!
(2n)!!
1
2n + 1
x
2n+1
, x (1, 1) .
8.41 Sa se gaseasca seriile Mac-Laurin ale funct iilor:
1) f (x) =
_
x
0
e
t
2
dt, 2) f (x) =
_
x
0
arctg t
t
dt, 3) f (x) =
_
x
0
ln (1 +t)
t
dt.
R: 1)

Inlocuind n dezvoltarea funct iei e
x
pe x prin t
2
si integrand ntre 0 si x,
obt inem:
_
x
0
e
t
2
dt =
n=0
(1)
n
1
n!
1
2n + 1
x
2n+1
, x R.
2)

Inlocuind n dezvoltarea funct iei arctg x pe x prin t, mpart ind prin t si integrand
ntre 0 si x obt inem:
_
x
0
arctg t
t
dt =
n=0
(1)
n
1
(2n + 1)
2
x
2n+1
, x [1, 1] .
3)
Inlocuindn dezvoltarea funct iei ln (1 +x) pe x prin t, mpart ind prin t si integrand
ntre 0 si x obt inem:
_
x
0
ln (1 +t)
t
dt =
n=1
(1)
n1
1
n
2
x
n
, x [1, 1] .
8.42 Sa se determine parametrii reali si a.. seriile:
1)
n=1
n
_
arctg
1
n
+ ln
_
1 +
1
n
_

n
+

n
2
_
. 2)
n=1
n
_
1 +e
1
n
+

n
+
1
n
2
_
sa e convergente.
R: 1) Se folosesc dezvoltarile n serii de puteri ale funct iilor arctg x si ln (1 +x) si se
gaseste = 2 si =
1
2
. 2) Se foloseste dezvoltarea lui e
x
si se obt ine = 1 si =
3
2
.
Capitolul 9
Elemente de geometrie
diferent iala
9.1 Curbe plane
9.1 Sa se gaseasca ecuat ia locului geometric al punctelor M din plan pentru care pro-
dusul distant elor la doua puncte date F
1
si F
2
, cu d(F
1
, F
2
) = 2c, este o constanta egala
cu a
2
( ovalele lui Cassini).
R: Alegem ca axa Ox dreapta F
1
F
2
, originea n mijlocul segmentului [F
1
F
2
]. Atunci
F
1
(c, 0), F
2
(c, 0). Pentru un punct oarecare al locului, M(x, y), avem:
d(M, F
1
) =
_
(x +c)
2
+y
2
, d(M, F
2
) =
_
(x c)
2
+y
2
.
Prin ipoteza d(M, F
1
) d(M, F
2
) = a
2
. De aici, dupa efectuarea calculelor, obt inem:
(x
2
+y
2
)
2
2c
2
(x
2
y
2
) = a
4
c
4
.
Pentru c = 0 se obt ine un cerc de raza a. Pentru c = a curba se numeste lemniscata lui
Bernoulli : (x
2
+y
2
)
2
= 2a
2
(x
2
y
2
). Luand x = r cos , y = r sin , obt inem ecuat ia n
coordonate polare a lemniscatei: r
2
= 2a
2
cos 2, cu
_
0,

4
_
3
4
,
5
4
_
7
4
, 2
.
9.2 Se da un cerc de diametru [[
OA[[ = 2a si tangenta n A. O coarda variabila care

trece prin O ntalneste cercul n P si tangenta n Q. Sa se gaseasca locul geometric al
punctului M de pe coarda pentru care

OM =
PQ (cissoida lui Diocles).

R: Fie x = 2a ecuat ia tangentei n A, y = tx o dreapta variabila prin origine si
(x a)
2
+ y
2
= a
2
ecuat ia cercului. Atunci: Q(2a, 2at), P
_
2a
1+t
2
,
2at
1+t
2
_
. Daca M(x, y)
este un punct curent al locului, scriind ca r =

OM =

PQ, gasim: x =
2at
2
1+t
2
, y =
2at
3
1+t
2
,
t R. Ecuat ia implicita a curbei este x(x
2
+y
2
) = 2ay
2
.
9.3 Dreapta x = a ntalneste axa Ox n punctul A si o dreapta oarecare prin O n
B. Pe dreapta OB se iau de o parte si de alta a lui B segmentele [BM
1
] si [BM
2
] a..
105
CAPITOLUL 9. ELEMENTE DE GEOMETRIE DIFERENT IAL
A 106
d(B, M
1
) = d(B, M
2
) = d(A, B). Sa se gaseasc a locul geometric al punctelor M
1
si M
2
.
Sa se dea o reprezentare parametrica a curbei loc geometric (strofoida).
R: Fie A(a, 0), B(a, ). Punctele M
1
, M
2
, A apart in cercului cu centrul n B si raza
, de ecuat ie: (x a)
2
+ (y )
2
=
2
. Dreapta (AB) are ecuat ia: y =

a
x. Eliminand
pe obt inem ecuat ia inplicita a locului: x(x a)
2
(2a x)y
2
= 0. Ecuat ia explicita a
curbei este:
y =
_
x(x a)
2
2a x
, x [0, 2a).
Punand
y
xa
= t, obt inem reprezentarea parametrica: x =
2at
2
1+t
2
, y =
at(t
2
1)
1+t
2
, t R.
9.4 Extremitat ile segmentului [AB] de lungime a alunec a pe axele Ox si Oy perpendi-
culare. Paralelele la axe prin A si B se intalnesc n C. Din C se coboara perpendiculara
CM pe AB. Sa se gaseasca locul geometric al punctului M (astroida).
R: Fie A(, 0), B(0, ) cu
2
+
2
= a
2
. Atunci: (AB)
x
+
y
1 = 0 sau x+y =
0. Cum C(, ) si v = N(, ) rezulta: (CM) (x ) (y ) = 0. Luand: =
a cos t, = a sint, obt inem reprezentarea parametrica a curbei: x = a cos
3
t, y = a sin
3
t,
t [0, 2). Eliminand parametrul t se gaseste ecuat ia implicita: x
2/3
+y
2/3
= a
2/3
.
9.5 Un cerc ((C, R) se rostogoleste fara alunecare pe axa Ox, adica [[
OI[[ = lg arc IM
(I ind punctul de contact). Sa se gaseasca locul geometric al unui punct M invariabil
legat de acest cerc (cicloida).
R: Fie t unghiul dintre

CI si

CM. Atunci: x
I
= lg arc OI = Rt si: x = x
I
Rsin t,
y = R Rcos t. Se obt ine: r = R(t sin t)i +R(1 cos t)j, t R.
9.6 Se dau: un cerc cu centrul n punctul C si raza d(O, C) = 2a si mediatoarea segmen-
tului [OC]. O coarda variabila care trece prin O ntalneste cercul n P si mediatoarea
segmentului [OC] n Q. Sa se gaseasca locul geometric al punctelor M de pe coarda
pentru care

OM =
PQ (trisectoarea lui Mac Laurin).

R: Fie y = tx ecuat ia secantei, (x 2a)
2
+y
2
= 4a
2
ecuat ia cercului si x = a ecuat ia
mediatoarei. Atunci: P
_
4a
1+t
2
,
4at
1+t
2
_
, Q(a, at). Scriind ca r =

OM =

PQ, obt inem
ecuat iile parametrice ale locului: x = a
t
2
3
t
2
+1
, y = at
t
2
3
t
2
+1
, t R. Ecuat ia carteziana
implicita este x(x
2
+y
2
) a(y
2
3x
2
) = 0.
9.7 Se da cercul C(O, a) si punctul A pe cerc. Fie P si Q doua puncte pe cerc ai caror
vectori de pozit ie

OP si

OQ fac cu

OA unghiurile 2 si respectiv . Sa se gaseasca
locul geometric al punctelor M de intersect ie a tangentelor n P si Q la cerc (Trisectoarea
lui Longchamps).
R:

In reperul n care axa Ox are direct ia si sensul lui
OA, avem P(a cos 2, a sin 2),

Q(a cos , a sin ) si deci tangentele n cele doua puncte au ecuat iile:
xcos 2 +y sin 2 a = 0, xcos y sin a = 0.
Eliminand pe ntre cele doua ecuat ii, observand ca y = xtg , se obt ine ecuat ia
carteziana implicita a curbei: x(x
2
y
2
) a(x
2
+y
2
) = 0.
A 107
9.8 Curba x = x(t), y = y(t) se numeste unicursala daca x(t) si y(t) sunt funct ii
rat ionale de t. Sa se arate ca o curba data printr-o reprezentare implicita de forma:
n
(x, y) +
n1
(x, y) = 0, unde
k
(x, y) este un polinom omogen de gradul k, este o
curba unicursala.
R: Luand y = tx, se obt ine reprezentarea parametrica:
x =
n1
(1, t)
n
(1, t)
, y = t
n1
(1, t)
n
(1, t)
.
9.9 Curba descrisa de un punct M situat pe un cerc de raza R, care se rostogoleste fara
alunecare pe un cerc x de raza R
0
, cele doua cercuri ind tangente exterior, se numeste
epicicloida. Sa se gaseasca o reprezentare parametrica a curbei.
R: O reprezentare parametrica a curbei este
x = (R
0
+R) cos t Rcos
R
0
+R
R
t, y = (R
0
+R) sin t Rsin
R
0
+R
R
t.
In particular, daca R = R
0
, curba se numeste cardioida si are ecuat ia carteziana
(x
2
+y
2
2Rx)
2
= 4R
2
(x
2
+y
2
).
9.10 Curba descrisa de un punct M situat pe un cerc de raza R, care se rostogoleste
far a alunecare pe un cerc x de raza R
0
, cele doua cercuri ind tangente interioare, se
numeste hipocicloida. Sa se gaseasca o reprezentare parametrica a curbei.
R: O reprezentare parametrica a curbei este
x = (R
0
R) cos t +Rcos
R
0
R
R
t, y = (R
0
R) sin t Rsin
R
0
R
R
t.
Pentru R
0
= 3R curba se numeste hipocicloida lui Steiner, iar pentru R
0
= 4R curba
obt inuta este astroida de ecuat ie carteziana x
2/3
+y
2/3
= R
2/3
0
.
9.11 Figura de echilibru a unui r greu si omogen, exibil dar inextensibil ale carui
capete sunt xate n doua puncte se numeste lant isor. Sa se gaseasca ecuat ia carteziana
explicita a curbei.
R: Ecuat ia sa carteziana explicita este y = a ch
x
a
.
9.12 Curba plana descrisa de un punct care se misca uniform pe o dreapta n rotat ie
uniforma n jurul unui punct x al ei O se numeste spirala lui Arhimede. Sa se gaseasca
ecuat ia explicita, n coordonate polare, a curbei.
R: Ecuat ia curbei este r = a.
9.13 Curba plana descrisa de un punct care se misca cu viteza proport ionala cu distan-
t a parcursa pe o dreapta n rotat ie uniforma n jurul unui punct x al ei O se numeste
spirala logaritmica. Sa se gaseasc a ecuat ia explicita a curbei, n coordonate polare.
A 108
R: Ecuat ia curbei este r = ke
m
.
9.14 Sa se gaseasca ecuat iile tangentei si normalei la curbele:
1) x = t
3
2t, y = t
2
+ 1 n punctul M
0
(1).
2) x = a cos
3
t, y = a sin
3
t (astroida) n punctul M(t).
3) x = a(t sin t), y = a(1 cos t) (cicloida) n punctul M(t).
4) y = x
2
+ 4x + 3, n punctele de abscise 1, 0, 1.
5) y = tg x, n punctele de abscise 0,

4
.
6) F(x, y) = x
3
+y
3
3axy = 0 (foliul lui Descartes) n M
0
_
3a
2
,
3a
2
_
.
7) F(x, y) = x(x
2
+y
2
) ay
2
= 0 (cissoida lui Diocles) n M
0
_
a
2
,
a
2
_
.
8) F(x, y) = (x
2
+ y
2
)
2
2a
2
(x
2
y
2
) = 0 (lemniscata lui Bernoulli) n punctul
M
0
(x
0
, y
0
).
9)
x
2
a
2
+
y
2
b
2
1 = 0,
x
2
a
2

y
2
b
2
1 = 0, y
2
= 2px n punctul M
0
(x
0
, y
0
) de pe curba.
R: 1) Ecuat iile tangentei si normalei ntr-un punct M
0
(t
0
) al curbei x = x(t), y = y(t)
sunt:
x x(t
0
)
x
(t
0
)
=
y y(t
0
)
y
(t
0
)
, x
(t
0
)(x x(t
0
)) +y
(t
0
)(y y(t
0
)) = 0.
Dar, x(1) = 1, y(1) = 2, x
(1) = 1, y
(1) = 2, deci:
x+1
1
=
y2
2
, x + 1 + 2(y 2) = 0.
2) x
(t) = 3a cos
2
t sin t, y
(t) = 3a sin
2
t cos t, ecuat ia tangentei: xsin t + y cos t
a sint cos t = 0, ecuat ia normalei: xcos t +y sin t a(1 2 cos
2
t) = 0.
3) x
(t) = a(1 cos t), y
(t) = a sint, ecuat ia tangentei: xsin t y(1 cos t) a(t

sin t) sin t +a(1 cos t)
2
= 0, ecuat ia normalei: (1 cos t)x +y sin t at(1 cos t).
6) Ecuat iile tangentei si normalei ntr-un punct M
0
(x
0
, y
0
) al curbei F(x, y) = 0 sunt:
F
x
(x
0
, y
0
)(x x
0
) +F
y
(x
0
, y
0
)(y y
0
) = 0,
x x
0
F
x
(x
0
, y
0
)
=
y y
0
F
y
(x
0
, y
0
)
.
F(
3a
2
,
3a
2
) = 0, M
0
apart ine curbei. F
x
_
3a
2
,
3a
2
_
= F
y
_
3a
2
,
3a
2
_
=
9
4
a
2
. Ecuat ia tangentei:
x +y 3a, ecuat ia normalei: x y = 0.
7) F
_
a
2
,
a
2
_
= 0, M
0
apart ine curbei. 4x 2y a = 0, 2x + 4y 3a = 0.
8) F
x
(x, y) = 4x(x
2
+y
2
a
2
), F
y
(x, y) = 4y(x
2
+y
2
+a
2
).
9) Ecuat iile tangentelor:
x
0
x
a
2
+
y
0
y
b
2
1 = 0,
x
0
x
a
2

y
0
y
b
2
1 = 0, y
0
y = p(x +x
0
).
9.15 Sa se scrie ecuat iile tangentelor la curba (() x = t
2
1, y = t
3
+1, t R, paralele
cu dreapta (D) 2x y + 3 = 0.
R: r
(t) N = 0, r
(t) = 2ti + 3t
2
j, N(2, 1), 4t 3t
2
= 0, t
1
= 0, t
2
=
4
3
, r
(0) = 0,
M
1
(1, 1) este punct singular, r
_
4
3
_
=
8
3
(i + 2j). Tangenta n M
2
_
7
9
,
91
27
_
are ecuat ia:
54x 27y + 49 = 0.
9.16 Sa se scrie ecuat iile tangentelor la curba (() x = t
3
, y = t
2
, care trec prin punctul
M
0
(7, 1).
R: M
0
/ (. r
(t) = 3t
2
i + 2tj. O dreapta prin M
0
de direct ie r
are ecuat ia:

(D)
x + 7
3t
2
=
y + 1
2t
, t ,= 0.
Punctul M(t
3
, t
2
) D, daca t
3
+ 3t 14 = 0, cu radacina t = 2, deci ecuat ia tangentei
este: x 3y + 4 = 0.
A 109
9.17 Fie T
0
si respectiv N
0
punctele n care tangenta si normala n punctul M
0
, de
abscisa x
0
, al curbei y = f(x), ntalnesc axa Ox si P
0
proiect ia punctului M
0
pe axa
Ox. Sa se arate ca segmentele: tangenta [M
0
T
0
], normala [M
0
N
0
], subtangenta [T
0
P
0
]
si subnormala [P
0
N
0
] sunt date de:
_
_
_
M
0
T
0
_
_
_ =
f(x
0
)
f
(x
0
)
_
1 +f
2
(x
0
),
_
_
_
M
0
N
0
_
_
_ = [f(x
0
)[
_
1 +f
2
(x
0
),
_
_
_
P
0
T
0
_
_
_ =
f(x
0
)
f
(x
0
)
,
_
_
_
P
0
N
0
_
_
_ = [f(x
0
)f
(x
0
)[ .
R: Tangenta si normala n punctul M
0
(x
0
, f(x
0
)) au ecuat iile:
y f(x
0
) = f
(x
0
)(x x
0
), x x
0
+f
(x
0
)(y f(x
0
)).
Facand pe y = 0, se obt in coordonatele punctelor T
0
si N
0
.
9.18 Tractricea este curba cu proprietatea ca n ecare punct al ei, segmentul tangenta
are lungimea constanta a. Sa se gaseasca ecuat ia acestei curbe.
R: Din [
y
y
[
_
1 +y
2
= a rezulta:
dx
dy
=
a
2
y
2
|y|
, de unde prin integrare gasim:
x(y) =
_
a ln
a +
_
a
2
y
2
y

_
a
2
y
2
_
, y [a, a].
O reprezentare parametrica a curbei se obt ine luand y = a sin t, t
_
2
,

2
:
_
x =
_
ln tg
t
2
+ cos t
_
, y = a sint, t
_
2
, 0
,
x =
_
ln ctg
t
2
cos t
_
, y = a sint, t
_
0,

2
.
9.19 Sa se gaseasca punctele multiple si ecuat iile tangentelor n aceste puncte ale curbe-
lor:
1) x(x
2
+y
2
) 2ay
2
= 0 (cissoida lui Diocles).
2) (x
2
+y
2
)(y a)
2
b
2
y
2
= 0 (concoida lui Nicomede)
3) (2a x)y
2
= x(x a)
2
(strofoida).
4) (x
2
+y
2
)
2
2a
2
(x
2
y
2
) = 0 (lemniscata lui Bernoulli).
5) (x
2
+y
2
2ax)
2
4a
2
(x
2
+y
2
) = 0 (cardioida).
R: 1) O(0, 0) este punct de ntoarcere, ecuat ia tangentei: y = 0.
2) O(0, 0) pentru b > a este nod, ecuat iile tangentelor: y =
a
b
2
a
2
x, pentru b < a
este punct izolat, iar pentru b = a este punct de ntoarcere, ecuat ia tangentei: x = 0.
3) M
0
(a, 0) este nod, ecuat iile tangentelor: y = (x a).
4) O(0, 0) este nod, ecuat iile tangentelor: y = x.
5) O(0, 0) este punct de ntoarcere, ecuat ia tangentei: y = 0.
9.20 Sa se calculeze lungimea arcului de curba:
1) y =
1
4
x
2
1
2
ln x, x [1, 4]. 2) x = 8at
3
, y = 3a(2t
2
t
4
), t [0,
2].
3) r = a(1 + cos ), [0, 2). 4) x = a cos
3
t, y = a sin
3
t, t
_
0,

2
.
A 110
R: 1) Daca y = f(x), x [a, b], atunci: s =
_
b
a
_
1 +f
2
(x) dx, deci:
s =
1
2
_
4
1
1+x
2
x
dx = 2 ln 2 +
15
2
.
2) Daca x = x(t), y = y(t), t [a, b], atunci: s =
_
b
a
_
x
2
(t) +y
2
(t) dt, deci:
s = 12a
_
2
0
t
_
1 +t
2
_
dt = 24a.
3) ds =
dr
2
+r
2
d
2
= 2a
cos

2
d, deci s = 2a
_
cos

2
d = 8a.
4) s = 3a
_
2
0
sin t cos tdt =
3
2
a.
9.21 Sa se calculeze curbura curbei:
1) x = a cos t, y = b sin t. 2) x = a cht, y = b sh t. 3) y = sin x.
4) y
2
= 2px. 5) y = a ch (
x
a
). 6) y = ln x.
R: 1) Pentru o curba data printr-o reprezentare parametrica x = x(t), y = y(t),
curbura are expresia:
(t) =
[x
(t)y
(t) x
(t)y
(t)[
(x
2
(t) +y
2
(t))
3/2
.
Se obt ine: =
ab
(a
2
sin
2
t+b
2
cos
2
t)
3/2
. 2) =
ab
(a
2
sh
2
t+b
2
ch
2
t)
3/2
.
3) Pentru o curba data prin reprezentarea y = f(x), curbura are expresia:
(x) =
[f
(x)[
(1 +f
2
(x))
3/2
.
Se obt ine: =
|sin x|
(1+cos
2
x)
3/2
. 4) =
p
(p+2x)
3/2
= p
2
/(y
2
+p
2
)
3/2
. 5) =
a
y
2
.
9.22 Sa se gaseasca curbura unei curbe data prin ecuat ia implicita F(x, y) = 0, ntr-un
punct ordinar al ei.
R: Presupunem F
y
,= 0, atunci y
(x) =
F
x
F
y
. Se obt ine:
=
F
xx
F
2
y
2F
xy
F
x
F
y
+F
yy
F
2
y
(F
2
x
+F
2
y
)
3/2
.
9.23 Sa se gaseasca punctele n care curbura ia o valoare extrema (varfurile curbei):
1) x = at d sin t, y = a d cos t. 2) y = e
x
R: 1) (t) = d
|a cos td|
(a
2
2ad cos t+d
2
)
3
,
(t) = a
sin t(a
2
+ad cos t2d
2
)
(a
2
2ad cos t+d
2
)
3
, pentru a cos t
d > 0 si
(t) = a
sin t(a
2
+ad cos t2d
2
)
(a
2
2ad cos t+d
2
)
3
, pentru a cos t d < 0, M
min
((2k + 1)a, a + d),
M
max
(2ka, a d), k Z.
2) (x) =
e
x
(1+e
2x
)
3
,
(x) =
e
x
(12e
2x
)
(1+e
2x
)
3
, M
max
_
1
2
ln 2,
1
2
_
.
9.24 Sa se gaseasca curbura unei curbe data n coordonate polare prin ecuat ia: r = r().
R: Deoarece x = r cos , y = r sin , o reprezentare parametrica a curbei este: x =
r() cos , y = r() sin . Se obt ine =
[r
2
+2r
2
rr
[
(r
2
+r
2
)
3/2
.
A 111
9.25 Sa se gaseasca nfasuratoarele familiilor de curbe plane:
1) (x )
2
+y
2
= a
2
. 2) (x )
2
+ (y )
2
=
2
.
3) xcos +y sin p = 0. 4) y
2
= (x )
3
.
5) y
3
= (x )
2
. 6) 3(y )
2
2(x )
3
= 0.
7) (1
2
)x + 2y a = 0. 8)
2
(x a) y a = 0.
R: 1) Se elimina ntre ecuat iile: F(x, y) = 0 si F
(x, y) = 0. Se obt ine: y = a.

2) x = 0, y = 0. 3) x
2
+y
2
= p
2
.
4) y = 0 este locul geometric al punctelor singulare.
5) y = 0 este locul geometric al punctelor singulare.
6) y = x este locul geometric al punctelor singulare, x y =
2
9
este nfasuratoarea.
7)
_
x
a
2
_
2
+y
2
=
a
2
4
. 8) y
2
+ 4a(x a) = 0.
9.26 Sa se gaseasca nfasuratoarea unei familii de drepte care formeaza cu axele de
coordonate un triunghi de arie constanta 2a.
R: Daca si sunt taieturile dreptei pe axe, atunci [[ = 4a si F(x, y, ) =
4ax +
2
y 4a = 0, F
(x, y, ) = 2y 4a = 0. Rezulta: xy = a
2
.
9.27 Sa se gaseasca nfasuratoarea unei familii de drepte pe care axele de coordonate
determina un segment de lungime constanta a.
R: Daca si sunt taieturile dreptei pe axe, atunci
2
+
2
= a
2
sau = a cos t,
= a sin t. Deci: F(x, y, t) = xsin t + y cos t a sin t cos t = 0, F
t
(x, y, t) = xcos t
y sin t a cos 2t = 0. Se obt ine astroida: x = a cos
3
t, y = a sin
3
t.
9.28 Sa se gaseasca ecuat iile evolutei curbelor:
1) x = a cos t, y = b sin t. 2) x = a ch t, y = b sh t.
3) y = x
2
. 4) y = ln x.
R: 1) x =
c
2
a
cos
3
t, y =
c
2
b
sin
3
t, c
2
= a
2
b
2
. 2) x =
c
2
a
ch
3
t, y =
c
2
b
sh
3
t,
c
2
= a
2
+ b
2
. 3) Luam x = t, y = t
2
. Obt inem: x = 4t
3
, y = 3t
2
+
1
2
. 4) Luam x = t,
y = ln t. Obt inem: x = 2t +
1
t
, y = ln t t
2
1.
9.29 Sa se gaseasca evolventa curbelor:
1) x
2
+y
2
= a
2
. 2) x = t, y =
t
2
4
.
3) y = a ch
x
a
care trece prin v arful ei.
R: 1) s = at, x = a cos t (k at) sin t, y = a sint + (k at) cos t.
2) x =
t
2
+
2
t
2
+4
_
k ln(t +
t
2
+ 4)
_
, y =
t
t
2
+4
_
k ln(t +
t
2
+ 4)
_
.
3) Se obt ine tractricea: x = a
_
ln tg
x
a
+ cos t
_
, y = a sin t.
9.30 Sa se gaseasca ramurile innite si asimptotele curbelor:
1) x =
2t
(t1)(t2)
, y =
t
2
(t1)(t3)
. 2) x =
2t1
t
2
1
, y =
t
2
t1
.
3) x =
t
2
t1
, y =
t
t
2
1
. 4) xy
2
y
2
4x = 0.
5) (x
2
y
2
)(x y) = 1.
A 112
R: 1) Ramuri innite pentru: t = 1, t = 2, t = 3. Asimptota orizontala: y = 4,
verticala: x = 3. Asimptota oblica: y =
1
4
x
1
4
.
2) y =
1
2
, x = 0, y = 2x +
1
2
. 3) x =
1
2
, y = 0, 2x 4y 3 = 0.
4) Luand y = t se obt ine reprezentarea parametrica: x =
t
2
t
2
4
, y = t. Asimptote:
y = 2, x = 1.
5) Luand x y = t se obt ine reprezentarea parametrica: x =
1+t
3
2t
2
, y =
1t
3
2t
2
.
Asimptote: y = x.
9.31 Sa se studieze variat ia si sa se reprezinte grac curbele:
1) x = t
3
+ 3t, y = 3t
2
.
2) x =
3at
1+t
3
, y =
3at
2
1+t
3
sau x
3
+y
3
= 3axy (foliul lui Descartes).
3) x
3
xy
2
+ 2y
2
= 0.
4) x = r(2 cos t + cos 2t), y = r(2 sin t sin 2t) (hipocicloida lui Steiner).
R: 1) 1. t R, lim
t
x(t) = , lim
t
y(t) = +. Curba are doua ramuri
innite. 2. x(t) = 0 pentru t
1
= 0, t
2,3
=
3, y(0) = 0, y(
3) = 9, y(t) = 0
pentru t
1
= 0, x(0) = 0. Curba intersecteaza axa Oy n doua puncte O(0, 0), A(0, 9).
3. Curba nu este periodica. 4. x(t) = x(t), y(t) = y(t), curba este simetrica fat a
de axa Oy. 5. x
(t) = 3(t
2
1), x
(t) = 0 pentru t = 1, x(1) = 2, y(1) = 3,

y
(t) = 6t, y
(t) = 0 pentru t = 0, x(0) = 0, y(0) = 0. 6. Ecuat ia implicita a curbei este:

F(x, y) = 27x
2
y
3
+ 18y
2
81y = 0, F
x
= 54x, F
y
= 3(y
2
12y + 27) si F
x
= 0,
F
y
= 0, F = 0 pentru x
0
= 0, y
0
= 9, M
0
(0, 9) este nod cu m
2
= 3
2
. 7. Tabelul de
variat ie:
t
3 1 0 1

3 +
x
0 + + + 0
x + 0 2 0 2 0
y
0 + + + + + +
y + 9 3 0 3 9 +
8. Nu exista asimptote.
2) t R 1. Curba este simetrica fat a de prima bisectoare, O(0, 0) nod, x = 0,
y = 0 tangente n origine. Tabelul de variat ie:
t 1 0
1
3
2
3
2 +
x
+ + + + + + 0
x 0 [ 0 a
3
4 a
3
2 0
y
0 + + + 0
y 0 [ 0 a
3
2 a
3
4 0
Asimptota: x +y +a = 0.
3) Luand y = tx se obt ine reprezentarea parametrica: x =
2t
2
t
2
1
, y =
2t
3
t
2
1
. Curba
este simetrica fat a de axa Ox. O(0, 0) este punct de ntoarcere. Tabelul de variat ie:
t
3 1 0 1

3
x
+ + + + + + 0
x 2 3 [ 0 [ 3 2
y
+ + 0 0 0 + +
y 3
3 [ 0 [ 3
3
A 113
Are trei asimptote: x = 2, x y + 1 = 0, x +y + 1 = 0.
4) t [0, 2]. Curba este simetrica fat a de axa Ox.
x
(t) = 2r sin t(1 + 2 cos t), x
(t) = 0 t
_
0,
2
3
, ,
4
3
, 2
_
,
y
(t) = 2r(1 cos t)(1 + 2 cos t), y
(t) = 0 t
_
0,
2
3
,
4
3
, 2
_
.
t = 0, t =
2
3
, t =
4
3
puncte singulare. Tabelul de variat ie:
t 0
2
3

4
3
2
x
0 0 + 0 0 + 0
x 3r
3
2
r r
3
2
r a
y
0 + 0 0 + 0
y 0
3
3
2
r 0
3
3
2
r 0
9.2 Curbe n spat iu
9.32 Se numeste elice curba descrisa de un punct de pe cilindrul x
2
+ y
2
= a
2
a carui
proiect ie n planul Oxy se deplaseaza cu viteza unghiulara constanta si a carui proiect ie
pe axa Oz se deplaseaza cu viteza constanta. Sa se gaseasca o reprezentare parametrica
a elicei si ecuat iile proiect iilor elicei pe planele de coordonate.
R: Proiect ia punctului M(x, y, z) de pe cilindru n planul Oxy are coordonatele:
x = a cos , y = a sin cu
d
dt
= , = const, deci = t. Proiect ia punctului M pe axa
Oz are cota z cu
dz
dt
= k, deci z = kt. Se obt ine reprezentarea parametrica: x = a cos t,
y = a sin t, z = kt. Daca se ia ca parametru, obt inem reprezentarea: x = a cos ,
y = a sin , z = b, cu b =
k
. Ecuat iile proiect iilor pe planele de coordonate sunt: pe

Oxy : x
2
+y
2
= a
2
, z = 0, pe Oyz : y = a sin
z
b
, x = 0, pe Ozx : x = a cos
z
b
, y = 0.
9.33 Un punct M se deplaseaza pe o generatoare a unui cilindru circular cu viteza
proport ionala cu drumul parcurs. Cilindrul se roteste n jurul axei sale cu viteza un-
ghiulara constanta. Sa se gaseasca ecuat iile parametrice ale curbei descrise de punctul
M.
R: x = a cos , y = a sin , z = be
k
.
9.34 Sfera de raza R si cilindrul circular de raz a
R
2
, care trece prin centrul sferei,
se intersecteaz a dupa o curba numita fereastra lui Viviani. Sa se gaseasca ecuat iile
carteziene implicite ale curbei, precum si o reprezentare parametrica a acesteia.
R: Alegem originea reperului n centrul sferei, axa Oz paralela cu axa cilindrului, axa
Ox trecand prin centrul cilindrului. Se obt ine: x
2
+ y
2
+ z
2
= R
2
, x
2
+ y
2
Rx = 0.
Deoarece ecuat ia cilindrului se scrie: (x
R
2
)
2
+ y
2
=
R
2
4
, luand: x
R
2
=
R
2
cos t,
y =
R
2
sin t, obt inem:
x =
R
2
(1 + cos t), y =
R
2
sint, z = Rsin
t
2
.
A 114
9.35 O dreapta prin origine, care nu este perpendiculara pe axa Oz, se roteste n jurul
acesteia cu viteza unghiulara constant a. Curba descrisa de un punct M care se de-
plaseaz a pe aceasta dreapta: 1) cu viteza constanta se numeste elice conica. 2) cu viteza
proport ionala cu distant a parcursa, d(O, M), se numeste spirala conica. Sa se gaseasca
ecuat iile parametrice ale acestor curbe.
R: Daca (r, , ) sunt coordonatele sferice ale punctului M, avem: = const,
_
,=

2
_
,
d
dt
= , deci = t.
1)
dr
dt
= k, deci r = kt. Obt inem: x = kt sin cos t, y = kt sin sin t, z = kt cos
sau, notand: a =
k
sin , b =
k
cos , gasim reprezentarea parametrica: x = acos ,

y = asin , z = b.
2)
dr
dt
= mr, deci r = r
0
e
mt
, obt inem reprezentarea: x = ae
k
cos , y = ae
k
sin ,
z = be
k
, n care k =
m
, a = r
0
sin , b = r
0
cos .
9.36 Axele a doi cilindri circulari, de raze a si b, se taie sub un unghi drept. Cilindrii
se intersecteaza dupa doua curbe nchise numite bicilindrice. Sa se gaseasca ecuat iile
carteziene implicite ale lor si o reprezentare parametrica. Sa se studieze cazul a = b.
R: x
2
+y
2
= a
2
, y
2
+z
2
= b
2
. O reprezentare parametrica (cu a b):
x = a cos t, y =
_
b
2
a
2
sin
2
t, z = a sint.
Pentru b = a se obt in doua elipse.
9.37 Se dau curba: r = a(sin t + cos t)i + a(sin t cos t)j + be
t
k si punctul ei M
0
(0).
Sa se gaseasca ecuat iile tangentei si ecuat ia planului normal n M
0
.
R: Deoarece r(0) = a(ij)+bk, r
(0) = a(i+j)bk, ecuat iile tangentei n M

0
la curba
se scriu
xa
a
=
y+a
a
=
zb
b
, iar ecuat ia planului normal va a(xa)+a(y+a)b(zb) = 0.
9.38 Se dau curba: y = 2e
x
, z = 3 ln(x + 1) si punctul M
0
(0, 2, 0) situat pe curba. Sa
se gaseasca ecuat iile tangentei si ecuat ia planului normal n M
0
.
R: Deoarece f
(0) = 2, g
(0) = 3, ecuat iile tangentei n M

0
vor
x
1
=
y2
2
=
z
3
, iar
ecuat ia planului normal: x + 2(y 2) + 3z = 0.
9.39 Se dau curba: F(x, y, z) = x
2
+ y
2
10 = 0, G(x, y, z) = y
2
+ z
2
25 = 0 si
punctul M
0
(1, 3, 4). Sa se gaseasca ecuat iile tangentei si ecuat ia planului normal n M
0
.
R: Deoarece grad F(x, y, z) = 2xi + 2yj, grad G(x, y, z) = 2yj + 2zk si deci v =
4(12i 4j + 3k), ecuat iile tangentei se scriu
x1
12
=
y3
4
=
z4
3
, iar ecuat ia planului
normal: 12(x 1) 4(y 3) + 3(z 4) = 0.
9.40 Se da curba r =3 cos t i + 3 sin t j + 4t k (elicea circulara). Sa se scrie ecuat iile
axelor si planelor reperului Frenet atasat curbei ntr-un punct M(t) al acesteia.
A 115
R: Deoarece r
= 3 sin t i = 3 cos t j +4k, ds = [[r
(t)[[ dt = 5 dt. Deducem ca t =

s
5
.
Avem deci
r = 3 cos
s
5
i+3 sin
s
5
j+
4
5
s k, r =
3
5
sin
s
5
i+
3
5
sin
s
5
j+
4
5
k, r =
3
25
cos
s
5
i
3
25
sin
s
5
j,
ncat
t =
1
5
(3 sin t i + 3 cos t j + 4 k), n = cos t isin t j, b =
1
5
(4 sin t i 4 cos t j + 3 k).
Ecuat iile axelor sunt:
- ecuat iile tangentei:
x 3 cos t
3 sin t
=
y 3 sin t
3 cos t
=
z 4t
4
,
- ecuat iile normalei principale:
x 3 cos t
cot t
=
y 3 sin t
sin t
=
z 4t
0
,
- ecuat iile binormalei:
x 3 cos t
4 sin t
=
y 3 sin t
4 cos t
=
z 4t
3
.
Ecuat iile planelor sunt:
- ecuat ia planului normal: 3xsint + 3y cos t + 4z 16t = 0,
- ecuat ia planului recticator: xcos t +y sin t 3 = 0,
- ecuat ia planului osculator: 4xsin t 4y cos t + 3z 12t = 0.
9.41 Sa se gaseasca ecuat iile tangentelor si planelor normale la curbele:
1) x =
1
cos t
, y = tg t, z = at, pentru t =

4
.
2) x = e
t
, y = e
t
, z = t
2
, pentru t = 1.
3) x = e
t
cos t, y = e
t
sin t, z = e
t
, pentru t = 0
4) x = a(t sin t), y = a(1 cos t), z = 4a sin
t
2
, pentru t =

2
.
R: 1)
x
2
=
y1
2
=
z
a
2
a
. 2)
xe
e
=
ye
1
e
1
=
z1
2
.
3) x = y + 1 = z. 4) x
a
2
( 4) = y =
1
2
z a.
9.42 Sa se gaseasca punctele curbei x = 3t t
3
, y = 3t
2
, z = 3t +t
3
, n care tangenta
la curba este paralela cu planul (P) 3x +y +z + 2 = 0.
R: M
1
(2, 12, 14), M
2
(2, 3, 4).
9.43 Sa se gaseasca ecuat iile tangentei si planului normal la elicea x = 2 cos t, y =
2 sin t, z = 4t, n punctul M
0
(0).
R: x = 2, 2y z = 0; y + 2z = 0.
A 116
9.44 Sa se gaseasc a curba de intersect ie a tangentelor la curba: x = t, y = t
2
, z = t
3
,
cu planul Oxy.
R: 4y = 3x
2
, z = 0.
9.45 Sa se arate ca curba: x = e
t/
2
cos t, y = e
t/
2
sin t, z = e
t/
2
este situata pe
conul: x
2
+y
2
z
2
= 0 si ntalneste generatoarele sale sub un unghi de 45
o
.
R: F(e
t/
2
cos t, e
t/
2
sin t, e
t/
2
) = 0. Generatoarea prin M(t) are ecuat iile:
x
e
t/
2
cos t
=
y
e
t/
2
sint
=
z
e
t/
2
.
cos =
vr
(t)
||v||||r
(t)||
=
2
2
, deci: = 45
0
.
9.46 Sa se gaseasca ecuat iile tangentei si planului normal la curba: x
2
+y
2
+z
2
= R
2
,
x
2
+y
2
Rx = 0 (fereastra lui Viviani) ntr-un punct M
0
(x
0
, y
0
, z
0
) al acesteia.
R: Ecuat iile tangentei:
xx
0
2y
0
z
0
=
yy
0
z
0
(R2x
0
)
=
zz
0
Ry
0
, iar ecuat ia planului normal:
2y
0
z
0
x +z
0
(R 2x
0
)y Ry
0
z = 0.
9.47 Fie data curba (() r = r(t) si e t(t) =
r
(t)
||r
(t)||
versorul tangentei la curba. Se
numeste indicatoare sferica a tangentelor la curba ( curba de ecuat ie: r = t(t). Sa se
gaseasca indicatoarea sferica a tangentelor la elicea r = a(i cos t +j sin t) +btk.
R: Cercul: x
2
+y
2
=
a
2
a
2
+b
2
, z =
b
a
2
+b
2
.
9.48 Sa se arate ca daca toate planele normale la o curba n spat iu trec printr-un punct
x, atunci curba este situata pe sfera cu centrul n acel punct (curba se numeste sferica).
R: Daca C(a, b, c) apart ine planului normal:
x
(t)(x x(t)) +y
(t)(y y(t)) +z
(t)(z z(t)) = 0,
atunci [(x(t) a)
2
+ (y(t) b)
2
+ (z(t) c)
2
]
= 0 sau
(x(t) a)
2
+ (y(t) b)
2
+ (z(t) c)
2
= R
2
.
9.49 Sa se gaseasca ecuat iile tangentei si planului normal la curba: x
2
= 2az, y
2
= 2bz,
n punctul ei M
0
(x
0
, y
0
, z
0
).
R: Ecuat iile tangentei:
xx
0
ay
0
=
yy
0
by
0
=
zz
0
x
0
y
0
, iar ecuat ia planului normal: ay
0
(x
x
0
) +by
0
(y y
0
) +x
0
y
0
(z z
0
) = 0, cu x
2
0
+y
2
0
> 0.
9.50 Sa se gaseasca ecuat iile planelor osculatoare ale curbei: x = t, y = t
2
, z = t
3
, care
trec prin punctul A(2,
1
3
, 6).
R: r
(t) r
(t) = 6t
2
i 6tj + 2k. Ecuat ia planului osculator n punctul M(t, t
2
, t
3
)
este: (P) 3t
2
(xt) 3t(y t
2
) +(z t
3
) = 0. A P daca 6t
2
t
3
+t 6 = 0, se obt ine:
t
1
= 1, t
2
= 6, t
3
= 1.
A 117
9.51 Sa se gaseasca ecuat ia planului osculator al curbei: x = a cos t, y = b sint, z = e
t
,
n punctul M
0
(0).
R: bx +ay +abz = 2ab.
9.52 Sa se gaseasca ecuat ia planului osculator la curba de intersect ie a sferei x
2
+y
2
+
z
2
= 9 cu cilindrul hiperbolic x
2
y
2
= 3 n punctul M
0
(2, 1, 2).
R: Daca y = f(x), z = g(x) este o reprezentare explicita a curbei, cu x = 2, f(2) = 1,
g(2) = 2, din f
2
(x) + g
2
(x) = 9 x
2
si f
2
(x) = x
2
3, gasim: f(x)f
(x) + g(x)g
(x) =
x, f(x)f
(x) = x, f(x)f
(x) + g(x)g
(x) = 1, f(x)f
(x) + f
2
(x) = 1, de unde:
f
(2) + 2g
(2) = 2, f
(2) = 2, f
(2) + 2g
(2) = 9, f
(2) = 3. Deci: f
(2) = 2,
g
(2) = 2, f
(2) = 3, g
(2) = 3, N = 3(4i j +k) si planul osculator are ecuat ia:

4x y +z 9 = 0.
9.53 Sa se arate ca curba: x = e
t
cos t, y = e
t
sin t, z = 2t este situata pe suprafat a:
x
2
+y
2
e
z
= 0 si ca planul osculator al curbei se confunda cu planul tangent la suprafat a.
R: F(e
t
cos t, e
t
sint, 2t) = 0. r
(t) r
(t) = 2e
t
(2i cos t + 2j sin t e
t
k),
iar grad F(e
t
cos t, e
t
sin t, 2t) = e
t
(2i cos t + 2j sint e
t
k).
9.54 Sa se demonstreze ca tangentele la curba r = a(i cos t +j sin t) +be
t
k intersecteaza
planul Oxy dupa un cerc.
R: r
= a(i sin t + j cos t) + be

t
k. Ecuat iile tangentei:
xa cos t
a sin t
=
ya sin t
a cos t
=
zbe
t
be
t
.
Pentru z = 0 se obt ine curba: x = a(cos t + sin t), y = a(sin t cos t), a carei ecuat ie
implicita este: x
2
+y
2
= 2a
2
.
9.55 Sa se demonstreze ca planele normale n orice punct al curbei: r = a(1 cos t)i +
aj sint + 2akcos
t
2
trec printr-un punct x si sa se determine acest punct.
R: xsin t +y cos t z sin
t
2
= 0, O(0, 0, 0).
9.56 Sa se determine versorii tangentei, normalei principale si binormalei, precum si
ecuat iile planelor normal, recticator si osculator al curbelor (, n punctele indicate:
1) r = e
t
i +e
t
j +tk
2, M
0
(0) (.
2) r = ti +t
2
j +e
t
k, M
0
(0) (.
3) r = ti +
t
2
2
j +
t
2
2
k, M
0
(1) (.
4) r = (t
2
1)i +t
2
j kln t, M
0
(1) (.
9.57 Sa se determine punctele curbei: r =
1
t
i + tj + (2t
2
1)k prin care se pot duce
binormale perpendiculare pe dreapta: x +y = 0, z = 4x.
R: t
3
3t 2 = 0, t
1
= t
2
= 1, t
3
= 2.
9.58 Sa se determine punctele de pe curba: r =
1
t
i+j ln [t[ +tk unde normala principala
este paralela cu planul: 5x + 2y 5z 4 = 0.
A 118
R: 2t
4
5t
3
+ 5t 2 = 0, t
1
= 2, t
2
=
1
2
, t
3,4
= 1.
9.59 Sa se gaseasc a lungimea arcului elicei: x = a cos t, y = a sin t, z = bt, cuprins
ntre punctul de intersect ie cu planul Oxy si un punct arbitrar M(t).
R: s = t
a
2
+b
2
.
9.60 Sa se gaseasca lungimea unei spire a curbei: x = a(t sin t), y = a(1 cos t),
z = 4a cos
t
2
, marginit a de doua puncte consecutive ale sale de intersect ie cu planul Oxz.
R: s = 2a
2
_
2
0
sin
t
2
dt = 8a
2.
9.61 Sa se gaseasca lungimea arcului curbei: x
3
= 3a
2
y, 2xz = a
2
, cuprins ntre planele
y =
a
3
, y = 9a.
R: Cu: x = t, y =
1
2a
2
t
3
, z =
a
2
2t
, obt inem: s =
_
3a
a
_
t
2
a
2
+
a
2
2t
2
_
dt = 9a.
9.62 Sa se arate ca lungimea curbei nchise: x = cos
3
t, y sin
3
t, z = cos 2t este 10.
R: s = 4
5
2
_
/2
0
sin 2tdt = 10.
9.63 Sa se gaseasca lungimea arcului curbei: x = a cht, y = a sh t, z = at, cu ex-
tremit at ile n punctele M
0
(0), M(t).
R: s = a
2 sh t.
9.64 Sa se gaseasca expresia elementului de arc al unei curbe:
1) n coordonate cilindrice. 2) n coordonate sferice.
R: 1) ds
2
= dr
2
+r
2
d
2
+dz
2
. 2) ds
2
= dr
2
+r
2
d
2
+r
2
sin
2
d
2
.
9.65 Sa se calculeze curbura si torsiunea curbelor:
1) x = a ch t, y = a sh t, z = at. 2) x = a cos t, y = a sin t, z = bt.
3) x = t cos t, y = t sin t, z = bt. 4) x = e
t
, y = e
t
, z = t
2.
5) x = 2t, y = ln t, z = t
2
. 6) x = cos
3
t, y = sin
3
t, z = cos 2t.
R: 1) = =
1
2a ch
2
t
. 2) =
a
a
2
+b
2
, =
b
a
2
+b
2
.
3) =
2
1+a
2
. 4) = =
2
(e
t
+e
t
)
2
.
5) = =
2t
(1+2t
2
)
2
. 6) =
3
25 sin t cos t
, =
4
25 sin t cos t
.
9.66 Sa se arate ca urmatoarele curbe sunt plane si sa se gaseasca ecuat iile planelor ce
le cont in:
1) x =
1 +t
1 t
, y =
1
1 t
2
, z =
1
1 +t
.
2) x = a
1
t
2
+b
1
t +c
1
, y = a
2
t
2
+b
2
t +c
2
, z = a
3
t
2
+b
3
t +c
3
.
A 119
R: 1) (r
, r
, r
) = 0. Daca Ax+By+Cz+D = 0 este planul ce cont ine curba, atunci:

Ax(t) +By(t) +Cz(t) +D = 0 pentru t R 1, +1, de unde: x 4y + 2z + 1 = 0.
2) (r
, r
, r
) = 0. Planul curbei:
x c
1
y c
2
z c
3
a
1
a
2
a
3
b
1
b
2
b
3
= 0.
9.67 Sa se gaseasca ecuat iile intrinseci ale curbelor:
1) x = a cht, y = a sh t, z = at. 2) x = ct, y = c
2 ln t, z =
c
t
.
R: 1) = =
a
2a
2
+s
2
. 2) = =
c
2
4c
2
+s
2
.
9.68 Sa se arate ca exista un vector a.. formulele lui Frenet sa se scrie sub forma:
t = t, n = n,

b = b.
R: Formulele lui Frenet sunt:

t = n, n = t + b,

b = n. Luam =
t +n +b. Se obt ine: = t +b.
9.3 Suprafet e
9.69

In planul Oxz se da curba (() x = f(u), z = g(u), u I R. Sa se gaseasca
o reprezentare parametrica a suprafet ei de rotat ie obt inuta prin rotirea curbei ( n jurul
axei Oz.
R: Punctul M (f (u) , 0, g (u)) ( descrie cercul de ecuat ii:
x
2
+y
2
+z
2
_
f
2
(u) +g
2
(u)
= 0, z = g (u) , sau x
2
+y
2
f
2
(u) = 0, z = g (u) .
Rezulta reprezentarea parametrica: x = f(u) cos v, y = f(u) sin v, z = g(u), (u, v)
I [0, 2).
9.70 Sa se gaseacsa cate o reprezentare parametrica pentru suprafet ele de rotat ie obt i-
nute prin rotirea curbei ( n jurul axei Oz, daca curba ( este:
1) Cercul x = a +b cos u, y = 0, z = b sin u, (a > b), u [0, 2).
2) Lant isorul x = a ch
u
a
, y = 0, z = u, u R.
3) Tractricea x = a sin u, y = 0, z = a(ln tg
u
2
+ cos u), u
_
4
,

4
_
.
R: 1) Torul x = (a + b cos u) cos v, y = (a + b cos u) sin v, z = b sin u, (u, v)
[0, 2) [0, 2).
2) Catenoidul x = a ch
u
a
cos v, y = a ch
u
a
sin v, z = u, (u, v) R[0, 2).
3) Pseudosfera x = a sin ucos v, y = a sin usin v, z = a(ln tg
u
2
+ cos u), (u, v)
_
4
,

4
_
[0, 2).
9.71 Numim elicoid suprafat a generata de o curba ( (numita prol) n miscare de
rotat ie n jurul unei axe () si n acelasi timp de translat ie paralela cu aceasta axa,
vitezele acestor miscari ind proport ionale. Sa se gaseasc a ecuat iile elicoidului.
A 120
R: Daca se ia axa Oz drept axa de rotat ie si se presupune ca la momentul t = 0 curba
( este situata n planul Oxz, deci x = f(u), y = 0, z = g(u). Avem: x = f(u) cos v,
y = f(u) sin v,
dz
dt
= a
dv
dt
, cu a = const si z [
t=0
= g(u). Ecuat iile elicoidului sunt:
x = f(u) cos v, y = f(u) sin v, z = g(u) +av.
9.72 Un elicoid se numeste (1) normal sau (2) oblic dupa cum prolul este o dreapta
perpendiculara sau nu pe axa de rotat ie. Sa se gaseasca ecuat iile acestora.
R: 1) Ecuat iile prolului sunt: x = u, y = 0, z = 0, ecuat ia elicoidului normal:
x = ucos v, y = usin v, z = av.
2) Ecuat iile prolului sunt: x = u, y = 0, z = mu, m ,= 0, ecuat ia elicoidului oblic:
x = ucos v, y = usin v, z = mu +av.
9.73 Pe suprafat a: x = u+cos v, y = usin v, z = u, se da punctul M
0
de coordonate
parametrice u
0
= 1, v
0
=

2
.
1) Sa se scrie ecuat iile tangentelor si planelor normale la curbele u = 1 si v =

2
.
2) Sa se gaseasca unghiul dintre curbele u = 1 si v =

2
n M
0
.
3) Sa se arate ca curba: u = sin v si curba u = 1 admit o tangenta comuna n M
0
.
R: 1)
x1
1
=
y
0
=
z
0
,
x1
1
=
y
1
=
z
, x 1 = 0, x +y +z (1 +
2
) = 0.
2) cos =
1
2+
2
. 3) Curba: x = sin v cos v, y = 0, z = cos v admite ca tangenta
n M
0
dreapta D.
9.74 Sa se gaseasca ecuat iile planelor tangente si normalelor la suprafet ele:
1) x = 2u v, y = u
2
+v
2
, z = u
3
v
3
, n punctul M
0
(3, 5, 7).
2) x = u +v, y = u v, z = uv, n punctul M
0
de coordonate parametrice (2, 1).
3) z = x
3
+y
3
, n punctul M
0
(1, 2, 9).
4) x
2
+y
2
+z
2
168 = 0, n punctul M
0
(3, 4, 12).
5) x
2
2y
2
3z
2
4 = 0, n punctul M
0
(3, 1, 1).
6)
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1 = 0, n punctul M
0
(x
0
, y
0
, z
0
) de pe suprafat a.
R: 1) N = r
u
r
v
, u
0
= 2, v
0
= 1, 18x + 3y 4z 41 = 0. 2) 3x y 2z 4 = 0.
3) N = pi qj +k, cu p = f
x
, q = f
y
, 3x +12y z 18 = 0. 4) N = F
x
i +F
y
j +F
z
k,
3x + 4y + 12z 169 = 0. 5) 3x 2y + 3z 4 = 0. 6)
x
0
x
a
2
+
y
0
y
b
2
+
z
0
z
c
2
1 = 0.
9.75 Sa se gaseasca ecuat ia planului tangent la:
1) Pseudosfera x = a sin ucos v, y = a sin usin v, z = a
_
ln tg
u
2
+ cos u
_
.
2) Elicoidul normal x = ucos v, y = usin v, z = au.
3) Torul x = (7 + 5 cos u) cos v, y = (7 + 5 cos u) sin v, z = 5 sin u, n punctul
M
0
(u
0
, v
0
), cu cos u
0
=
3
5
, cos v
0
=
4
5
, u
0
, v
0

_
0,

2
_
.
R: 1) xcos ucos v +y cos usin v z sin u +a(ln tg
u
2
) sin u) = 0.
2) axsin v ay cos v +uz auv = 0,
xucos v
a sin v
=
yusin v
a cos v
=
zav
u
.
3) 12x + 9y + 29z 230 = 0.
9.76 Sa se gaseasca ecuat ia planului tangent suprafet ei: xyz = 1, paralel cu planul:
x +y +z = 0.
A 121
R: y
0
z
0
= 1, x
0
z
0
= 1, x
0
y
0
= 1, cu x
0
y
0
z
0
= 1, M
0
(1, 1, 1), x +y +z 3 = 0.
9.77 Sa se arate ca planele tangente la suprafat a xyz = a
3
formeaza cu planele de
coordonate un tetraedru de volum constant.
R: Planul tangent la suprafat an punctul ei M
0
(x
0
, y
0
, z
0
) are ecuat ia: y
0
z
0
x+z
0
x
0
y+
x
0
y
0
z 3a
3
= 0. Se obt ine 1 =
9a
3
2
.
9.78 Sa se arate ca planele tangente la suprafat a z = x
3
+y
3
n punctele M
0
(, , 0)
formeaz a un fascicul.
R:
2
(x +y) z = 0.
9.79 Sa se gaseasca prima forma fundamentala a urmatoarelor suprafet e de rotat ie:
1) x = f(u) cos v, y = f(u) sin v, z = g(u).
2) x = Rcos ucos v, y = Rcos usin v, z = Rsin u (sfera).
3) x = a cos ucos v, y = a cos usin v, z = c sin v (elipsoidul de rotat ie).
4) x = a ch ucos v, y = a ch usin v, z = c sh u (hiperboloidul cu o panza).
5) x = a sh ucos v, y = a sh usin v, z = c sh u (hiperboloidul cu doua panze).
6) x = ucos v, y = usin v, z = u
2
(paraboloidul de rotat ie).
7) x = Rcos v, y = Rsin v, z = u (cilindrul circular).
8) x = ucos v, y = usin v, z = ku (conul circular).
9) x = (a +b cos u) cos v, y = (a +b cos u) sin v, z = b sin u (torul).
10) x = a ch
u
a
cos v, y = aa ch
u
a
sin v, z = u (catenoidul).
11) x = a sin ucos v, y = a sin usin v, z = a
_
ln tg
u
2
+ cos u
_
(pseudosfera).
R: Prima forma fundamentala a suprafet ei este (dr) = Edu
2
+ 2Fdudv + Gdv
2
,
unde E = r
2
u
, F = r
u
r
v
, G = r
2
v
. Se obt ine:
1) (du, dv) = (f
2
(u) +g
2
(u))du
2
+f
2
(u)dv
2
. 2) (du, dv) = R
2
(du
2
+ cos
2
v dv
2
).
3) (du, dv) = (a
2
sin
2
u +c
2
cos
2
u)du
2
+a
2
cos
2
udv
2
.
4) (du, dv) = (a
2
sh
2
u +c
2
ch
2
u)du
2
+a
2
ch
2
udv
2
.
5) (du, dv) = (a
2
ch
2
u +c
2
sh
2
u)du
2
+a
2
sh
2
udv
2
.
6) (du, dv) = (1 +u
2
)du
2
+u
2
dv
2
. 7) (du, dv) = du
2
+R
2
dv
2
.
8) (du, dv) = (1 +k
2
)du
2
+u
2
dv
2
. 9) (du, dv) = b
2
du
2
+ (a +b cos u)
2
dv
2
.
10) (du, dv) = ch
2 u
a
du
2
+a
2
ch
2 u
a
dv
2
. 11) (du, dv) = a
2
ctg
2
udu
2
+a
2
sin
2
udv
2
.
9.80 Se da suprafat a: x = u
2
+v
2
, y = u
2
v
2
, z = uv.
1) Sa se gaseasca prima forma fundamentala a suprafet ei.
2) Sa se calculeze elementul de arc al curbelor: u = 2, v = 1, v = au.
3) Sa se calculeze lungimea arcului curbei v = au cuprins ntre punctele sale de
intersect ie cu curbele u = 1, u = 2.
R: 1) (du, dv) = (8u
2
+v
2
)du
2
+ 2uvdudv + (8v
2
+u
2
)dv
2
.
2) ds =
_
(du, dv) = 2
2v
2
+ 1dv, ds =
8u
2
+ 1du, ds = 2u
2a
4
+a
2
+ 2du.
3) s = 3
2a
4
+a
2
+ 2.
9.81 Sa se gaseasca unghiul dintre liniile u + v = 0, u v = 0 de pe elicoidul normal:
x = ucos v, y = usin v, z = av.
A 122
R: cos =
_
1 a
2
_
/
_
1 +a
2
_
.
9.82 Sa se gaseasca unghiul dintre liniile v = 2u, v = 2u de pe o suprafat a a carei
prima forma fundamentala este (du, dv) = du
2
+dv
2
.
R: cos = 3/5.
9.83 Sa se gaseasc a unghiul dintre liniile v = u + 1, v = 3 u de pe suprafat a: x =
ucos v, y = usin v, z = u
2
.
R: cos = 2/3.
9.84 Sa se gaseasca aria triunghiului curbiliniu marginit de liniile u = av si v = 1 de
pe o suprafat a a carei prima forma fundamentala este (du, dv) = du
2
+ (u
2
+a
2
)dv
2
.
R: Elementul de arie al suprafet ei r = r(u, v) este: dS =

EGF
2
dudv.

In cazul
nostru: dS =
u
2
+a
2
dudv. Deci
/ =
_
1
0
__
av
av
_
u
2
+a
2
du
_
dv = a
2
_
2
3

1
3
2 + ln
_
1 +
2
_
_
.
9.85 Sa se gaseasc a aria patrulaterului curbiliniu marginit de liniile u = 0, u = a, v = 0
si v = 1 de pe elicoidul normal: x = ucos v, y = usin v, z = av.
R: / =
1
2
a
2
_
2 + ln(1 +
2)
_
.
Capitolul 10
Integrala Riemann si extinderi
10.1 Primitive. Integrala nedenita
10.1 Sa se calculeze integralele:
1)
_
_
6x
2
+ 8x + 3
_
dx. 2)
_
_
2pxdx. 3)
_
dx
n
x
.
4)
_
dx
8 x
2
. 5)
_
dx
x
2
+ 7
. 6)
_
dx
x
2
10
.
R: 1) 2x
3
+ 4x
2
+ 3x +C, 2)
2
3
x
2px +C, 3)
n
n1
x
1
1
n
+C,
4) arcsin
1
4
x
2 +C, 5)
1
7
arctg
x
7
+C, 6)
1
2
10
ln
10
x+
10
+C.
1)
_
xdx
(x 1) (x + 1)
2
. 2)
_
dx
x
3
2x
2
+x
. 3)
_
dx
2x
2
+ 3x + 2
.
4)
_
dx
(x
2
+ 4x + 5)
2
. 5)
_
dx
x
4
+ 1
. 6)
_
x
4
dx
x
3
1
.
R: 1)
1
4
ln
x1
x+1

1
2(x+1)
+C. 2) ln
x
x1

1
x1
+C.
3)
2
7
arctg
1
7
(4x + 3) +C. 4)
1
2
x+2
x
2
+4x+5
+
1
2
arctg (x + 2) +C.
5)
1
8
2 ln
x
2
+x
2+1
x
2
x
2+1
+
1
4
2arctg
_
x
2 + 1
_
+
1
4
2arctg
_
x
2 1
_
+C.
6)
1
2
x
2
+
1
3
ln (x 1)
1
6
ln
_
x
2
+x + 1
_
+
1
3
3arctg
1
3
(2x + 1) +C.
10.3 Sa se calculeze, efectuand schimbarea de variabila indicata:
1)
_

ln x
x
dx, t = ln x. 2)
_
e
x
e
x
+ 1
dx, t = e
x
.
123
CAPITOLUL 10. INTEGRALA RIEMANN SI EXTINDERI 124
3)
_
dx
1 25x
2
, t = 5x. 4)
_
x
3
dx
1 x
8
, t = x
4
.
5)
_
cos x
a
2
+ 2 sin
2
x
dx, t =
1
a
sin x. 6)
_
dx
sin
2
x + 2 cos
2
x
, t =
1
2
tg x.
7)
_
cos x
_
2 + cos (2x)
dx, t =
_
2
3
sin x. 8)
_
xdx
1 +x
4
, t
2
= 1 +
1
x
4
.
R: 1)
2
3
ln
3
2
x +C. 2) ln (e
x
+ 1) +C.
3)
1
5
arcsin 5x +C. 4)
1
4
arcsin x
4
+C.
5)
1
|a|
2
arctg
_
2
|a|
sin x
_
+C. 7)
1
2
2 arcsin
_
1
3
6 sin x
_
+C.
8)
1
2
ln
_
x
2
+
1 +x
4
_
+C.
1)
_
x
_
1 x
2
_
1 +x
4
dx. 2)
_
2
x
1 4
x
dx. 3)
_ _
x +
1
3
x
_
2
dx.
4)
_
2
x
3
2x
5
3x
dx. 5)
_
(tg x + ctg x)
2
dx. 6)
_
x
1 x
2
e
arcsin x
dx.
7)
_
ln
3
x
x
2
dx. 8)
_
e
ax
cos (bx) dx. 9)
_
_
x
2
+ 1dx.
10)
_
_
9 x
2
dx. 11)
_
x
1 x
3
dx. 12)
_
_
x
2
+x + 1dx.
R: 1)
1
2
arctg x
2
1
4
ln
_
1 +x
4
_
+C. 2) t = 2
x
, da:
1
ln 2
arcsin t +C.
3)
1
2
x
2
+
12
7
(
6
x)
7
+ 3
3
x +C. 4)
1
ln 2+3 ln 5+2 ln 3
2
x
3
2x
5
3x
+C.
5) tg x ctg x +C. 6) t = arcsin x, da:
1
2
e
t
(sin t cos t) +C.
7)
ln
3
x
x

3
x
ln
2
x
6
x
ln x
6
x
+C.
8)
a
a
2
+b
2
e
ax
cos bx +
b
a
2
+b
2
e
ax
sin bx +C.
9)
1
2
x
_
(x
2
+ 1) +
1
2
ln
_
x +
_
(x
2
+ 1)
_
+C.
10)
1
2
x
_
(9 x
2
) +
9
2
arcsin
1
3
x +C. 11) t
2
= x
3
, da:
2
3
arcsin t +C.
12)
1
4
(2x + 1)
x
2
+x + 1 +
3
8
ln
_
x +
1
2
+
x
2
+x + 1
_
+C.
10.5 Sa se gaseasca formule de recurent a pentru integralele:
1) I
n
(x) =
_
sin
n
xdx. 2) J
n
(x) =
_
cos
n
xdx.
R: 1) I
n
(x) =
n1
n
I
n2
(x)
1
n
sin
n1
xcos x, n 2.
2) J
n
(x) =
n1
n
J
n2
(x) +
1
n
cos
n1
xsinx, n 2.
10.6 Sa se gaseasca formule de recurent a pentru integralele:
1) I
n
(x) =
_
dx
cos
n
x
. 2) I
n
(x) =
_
x
n
e
x
dx.
R: 1) I
n+2
(x) =
1
(n+1) cos
n+1
x
+
n
n+1
I
n
(x). 2) I
n
(x) = x
n
e
x
+nI
n1
(x).
1)
_
_
x
2
+ 3x 2dx. 2)
_
x
4
+ 1
x
3
+ 1
dx. 3)
_
dx
x
3
+x
5
.
4)
_
x + 1
x
4
+x
2
+ 1
dx. 5)
_
dx
x(x + 1) (x + 2)
. 6)
_
3x 1
x
2
4x + 8
dx.
7)
_
dx
(x
2
+ 1)
2
. 8)
_
x
2
+ 1
(x 1)
3
(x + 3)
dx. 9)
_
dx
2x
2
+ 3x + 2
.
R: 1)
1
4
(2x + 3)
_
(x
2
+ 3x 2) +
1
8
arcsin (2x 3) +C.
2)
1
2
x
2
+
2
3
ln (x + 1)
1
3
ln
_
x
2
x + 1
_
+C.
3)
_
dx
x
3
+x
5
=
1
2x
2
ln x +
1
2
ln
_
x
2
+ 1
_
+C.
4)
1
4
ln
_
x
2
+x+1
x
2
x+1
_
1
6
3arctg
1
3
(2x + 1) +
1
2
3arctg
1
3
(2x 1) +C.
5)
1
2
ln x ln (x + 1) +
1
2
ln (x + 2) +C.
6)
3
2
ln
_
x
2
4x + 8
_
+
5
2
arctg
x2
2
+C. 7)
1
2
x
x
2
+1
+
1
2
arctg x +C.
8)
1
4(x1)
2

3
8(x1)
+
5
32
ln
x1
x+3
+C. 9)
2
7
arctg
1
7
(4x + 3) +C.
1)
_
x +
x
2
+x + 1
x + 1 +
x
2
+x + 1
dx. 2)
_
sin
x + cos
x sin 2
x
dx. 3)
_
3x + 2
x
2
+x + 2
dx.
4)
_
dx
x (
4
x + 1)
10
. 5)
_
dx
x
4
1 +x
2
. 6)
_
dx
5 + 4 sin x
.
7)
_
dx
2 sin x cos x + 5
. 8)
_
dx
sin 2x cos 2x
. 9)
_
tg
7
xdx.
1)
_
dx
x
3
x
2
+ 1
. 2)
_
dx
4
x
4
+ 1
. 3)
_
3
_
1 +
4
xdx.
4)
_
dx
(1 +x)
1 +x +x
2
. 5)
_
x + 1
x
2
+ 4x + 5
dx. 6)
_
1 + sin x
1 + cos x
e
x
dx.
1)
_
_
e
3x
e
x
_
dx
e
4x
e
3x
+ 2e
2x
e
x
+ 1
. 2)
_
cos x cos 3x cos 6xdx.
3)
_
x
2
+x + 1
x
2
+ 1
e
arctg x
dx. 4)
_
2x 5
(x 1) (x 2) (x 3) (x 4) +a
dx, a > 1.
R: 1) ln
e
2x
e
x
+1
e
2x
+1
+C. 2)
1
8
_
1
2
sin 4x +
1
4
sin 8x + sin 2x +
1
5
sin 10x
_
.
3) xe
arctg x
+C. 4)
1
a1
arctg
x
2
5x+5
a1
+C.
I (x) =
_
sin 2x
3 + sin 4x
dx, J (x) =
_
cos 2x
3 + sin 4x
dx.
R: I (x) +J (x) =
1
2
arcsin
_
2 cos 4x
_
+C
1
, I (x) J (x) =
1
3 + sin 4x +C
2
.
I (x) =
_
sin x
e
x
+ sin x + cos x
dx, J (x) =
_
e
x
+ cos x
e
x
+ sin x + cos x
dx.
R: Se calculeaza J (x) +I (x) si J (x) I (x).
1)
_
x
3
+ 2x
2
+ 3x + 4
x
2
+ 2x + 2
dx. 2)
_
x
4
+ 4x
2
x
2
+ 4
dx.
R: 1) Integrala se poate pune sub forma:
_
x
3
+ 2x
2
+ 3x + 4
x
2
+ 2x + 2
dx =
_
x
2
+x +
_
_
x
2
+ 2x + 2 +
_
dx
x
2
+ 2x + 2
.
Derivand si identicand coecient ii, obt inem: =
1
3
, =
1
6
, =
7
6
, =
5
2
. Gasim:
_
1
3
x
2
+
1
6
x +
7
6
_
_
x
2
+ 2x + 2 +
5
2
ln
x + 1 +
_
x
2
+ 2x + 2
+C.
2)
_
1
4
x
3
+
1
2
x
_
x
2
+ 4 2 ln
_
x +
x
2
+ 4
_
+C.
10.14 Sa se calculeze integralele binome:
1)
_
dx
x
3
x
2
+ 1
. 2)
_
dx
4
x
4
+ 1
. 3)
_
xdx
_
1 +
3
x
2
. 4)
_
3
_
1 +
4
x
dx.
R: 1)
m+1
n
= 0, se efectueaza schimbarea de variabila: x
2
+ 1 = t
3
si se obt ine:
3
2
_
tdt
t
3
1
=
1
2
ln
t 1
t
2
+t + 1
+
1
2
3 arctan
1
3
(2t + 1)
3 +C.
2)
m+1
n
+p = 0, se efectueaza schimbarea de variabila: 1 +x
4
= t
4
si se obt ine:
_
t
2
t
4
1
dt =
1
4
ln
_
t + 1
t 1
_
1
2
arctg t +C.
3)
m+1
n
= 3, se efectueaza schimbarea de variabila: 1 +x
2
3
= t
2
si se obt ine:
3
_
_
t
2
1
_
2
dt =
3
5
t
5
2t
3
+ 3t +C.
4)
m+1
n
= 2, se efectueaza schimbarea de variabila: 1 +x
1
4
= t
3
si se obt ine:
12
_
t
3
_
t
3
1
_
dt =
12
7
t
7
3t
4
+C.
10.15 Sa se calculeze integralele binome:
1)
_
x
3
_
2x
2
+ 1
_
3
2
dx. 2)
_
dx
x
2
3
_
(x
3
+ 2)
5
.
3)
_
dx
x
3
3
_
1 +
4
x
3
. 4)
_
3
x
_
5x
3
x + 3dx.
10.2 Integrala denita
1) lim
n
n
n
k=1
1
n
2
+k
2
=

4
. 2) lim
n
n
k=1
1
n +k
= ln 2.
R: Se va observa ca:
1) lim
n
n
n
k=1
1
n
2
+k
2
=
_
1
0
1
1 +x
2
dx. 2) lim
n
n
k=1
1
n +k
=
_
1
0
1
1 +x
dx.
10.17 Sa se calculeze limitele urmatoarelor siruri:
1) a
n
=
1
n
5
n
k=1
k
4
. 2) a
n
=
1
n
2
n
k=1
k
2
n +k
.
3) a
n
=
1
n
2
n
k=1
e
k
2
n
2
. 4) a
n
=
1
n
n
k=1
_
1 +
k
2
n
2
.
10.18 Sa se calculeze, aplicand formula lui Leibniz-Newton:
1)
_
1
0
1
1 +x
dx. 2)
_
x
x
e
t
dt. 3)
_
x
0
cos t dt.
4)
_
1
0
x
x
2
+ 3x + 2
dx. 5)
_
4
1
1 +
x
x
2
dx. 6)
_
1
2
x
x
2
+ 4x + 5
dx.
7)
_
1
0
x
3
x
8
+ 1
dx. 8)
_
3
6
ctg xdx. 9)
_
1
0
chxdx.
R: 1) ln 2. 2) e
x
e
x
. 3) sin x. 4) 2 ln 3 3 ln 2. 5)
7
4
. 6)
1
2
ln 2
1
2
.
7)
1
16
. 8)
1
2
ln 3. 9)
1
2
_
e e
1
_
.
I
n
=
_
2
0
sin
n
xdx =
_
2
0
cos
n
xdx, I
n
=
n 1
n
I
n2
.
10.20 Sa se gaseasc a o formula de recurent a pentru integrala:
J
n
=
_
1
0
_
1 x
2
_
n
dx.
R: Efectuand schimbarea de variabila x = sin t, se obt ine J
n
= I
2n+1
, de unde:
J
n
=
2n
2n+1
J
n1
.
1)
_
1
0
x
2
e
x
dx. 2)
_
b
a
_
(x a) (x b)dx. 3)
_

0
x
2
cos xdx.
4)
_
1
0
x + 1
1 +x
2
dx. 5)
_
1
0
dx
e
x
+e
x
. 6)
_
4
0
x
_
x
2
+ 9dx.
7)
_
4
0
ln (1 + tg x) dx. 8)
_
1
0
x
2
arctg xdx. 9)
_

0
x
2
sin
2
xdx.
R: 1) e 2. 2)

8
(b a)
2
. 3) 2. 4)

2 1 + ln
_
2 + 1
_
.
5) arctge
1
4
. 6)
98
3
. 7)

8
ln 2. 8)
1
6
_
2
1 + ln 2
_
. 9)

2
6

4
.
1)
_
2
0
e
x
max
_
1, x
2
_
dx. 2)
_
3
2
dx
(x + 1)
x
2
1
. 3)
_
2
2
min x 1, x + 1 dx.
4)
_
e
1
sin (ln x)
x
dx. 5)
_
2
0
dx
x + 1 +
_
(x + 1)
3
. 6)
_
3
3
xsinx
cos
2
x
dx.
R: 1) 2e
2
e. 2)
1
2

1
3
. 3) 2. 4) 1 cos 1. 5)

6
. 6) 2
_
2
3
ln
_
tg
5
12
__
.
1) I =
_
2
2
cos x
(2 cos
2
x) (e
x
+ 1)
dx. 2) I =
_
2n
0
sin (x + sin x) dx, n N
.
R: 1) Avem, succesiv:
I =
_
0
2
cos x
_
1 + sin
2
x
_
(e
x
+ 1)
dx +
_
2
0
cos x
_
1 + sin
2
x
_
(e
x
+ 1)
dx =
=
_
2
0
cos x
1 + sin
2
x
dx = arctg (sin x)[
2
0
=

4
.
2) Efectuam schimbarea de variabila: x = t +n si obt inem succesiv:
I =
_
n
n
sin [t +n + sin (t +n)] dt =
_
n
n
sin [n + (t + (1)
n
sin t)] dt =
= (1)
n
_
n
n
sin [t + (1)
n
sin t] dt = 0,
deoarece integrantul este o funct ie impara.
lim
0
_

1 cos kx
1 cos x
dx = k, k Z.
R: Notam I (k) =
_
1cos kx
1cos x
dx. Se constata ca:
I (k + 1) +I (k 1) = 2I (k) + 2
_

cos kxdx,
de unde: lim
0
[I (k + 1) 2I (k) +I (k 1)] = 0. Cum lim
0
I (1) = , presupunand
ca lim
0
I (k 1) = (k 1) si lim
0
I (k) = k, rezulta prin induct ie, ca
lim
0
I (k + 1) = (k + 1) .
10.25 Sa se calculeze integrala:
I
m,n
=
_
b
a
(x a)
m
(b x)
n
dx, cu m, n N.
R: Integrand prin part i, se obt ine formutla de recurent a: I
m,n
=
m
n+1
I
m1,n+1
, de
unde rezulta:
I
m,n
=
n!m!
(n +m+ 1)!
(b a)
n+m+1
.
10.26 Daca a < b si n N
, sa se arate ca:
lim
n
_
_
b
a
(x a)
n
(b x)
n
dx
_1
n
=
1
4
(b a)
2
.
R: Din exercit iul precedent avem ca:
I
n,n
=
(n!)
2
(2n + 1)!
(b a)
2n+1
,
de unde rezulta ca
lim
n
n
_
I
n,n
= (b a)
2
lim
n
n
(n!)
2
(2n + 1)!
=
1
4
(b a)
2
.
10.27 Fie f : [0, 1] R o funct ie continua. Sa se arate ca:
_

0
x f (sin x) dx =
_

0
f (sin x) dx.
R:

Intr-adevar,
_

0
x f (sin x) dx =
_
2
0
x f (sin x) dx +
_

2
x f (sin x) dx.
Efectuand n cea de-a doua integrala schimbarea de variabila: x = t, obt inem:
_

2
x f (sin x) dx =
_
2
0
f (sin x) dx
_
2
0
x f (sin x) dx.
10.28 Fie f : [0, a] R
+
o funct ie integrabila. Sa se arate ca:
_
a
0
f (x)
f (x) +f (a x)
dx =
a
2
.
R: Fie:
I (a) =
_
a
0
f (x)
f (x) +f (a x)
dx, J (a) =
_
a
0
f (a x)
f (x) +f (a x)
dx.
Evident: I (a)+J (a) = a. Efectuandn integrala J (a) schimbarea de variabila x = at,
obt inem ca J (a) = I (a). Deci, I (a) =
a
2
.
1)
_
2
0
(cos x)
sin x
(cos x)
sin x
+ (sin x)
cos x
dx. 2)
_
2
0
sin
2
x + sin x
sin x + cos x + 1
dx.
R: 1) Fie f (x) = (cos x)
sin x
. Atunci, f
_
2
x
_
= (sin x)
cos x
si conform exercit iului
precedent valoarea integralei este

4
. 2) Fie f (x) = sin
2
x + sin x. Atunci, f
_
2
x
_
=
cos
2
x + cos x si deci valoarea integralei este

4
.
10.30 Fie f : [1, 1] R o funct ie continua cu proprietatea ca f (x) + f (x) = ,
pentru orice x [1, 1]. Sa se calculeze integrala:
I =
_
(2n+1)
0
f (cos x) dx.
R: Efectuam schimbarea de variabila: x = (2n + 1) t. Obt inem:
I =
_
(2n+1)
0
f (cos t) dt.
Dar: f (cos t) = f (cos t) si deci I =
2n+1
2

2
.
10.31 Fie f : R
+
R
+
o funct ie continua strict crescatoare pe R
+
si f (0) = 0. Sa
se stabileasca inegalitatea lui Young:
_
a
0
f (x) dx +
_
b
0
f
1
(y) dy ab, a, b R
+
.
R: Fie S
x
aria suprafet ei cuprinsa ntre gracul funct iei f, axa Ox si dreapta x = a
si S
y
aria suprafet ei cuprinsa ntre gracul funct iei f, axa Oy si dreapta y = b. Evident:
S
x
+S
y
ab, de unde inegalitatea ceruta.
10.32 Fie F (x) =
_
x
3
0
e
t
2
dt. Sa se calculeze F
(x).
R: Notam cu G(t) o primitiva a funct iei e
t
2
, deci a.. G
(t) = e
t
2
. Atunci:
F (x) = G(t)[
x
3
0
= G
_
x
3
_
G(0) , de unde, F
(x) = 3x
2
G
(x) = 3x
2
e
x
6
.
10.33 Fie f : R R o funct ie derivabila pe R, denita prin: f (x) =
_
arctg x
0
e
tg
2
t
dt.
Sa se calculeze f
(x) si sa se arate ca:

_
1
0
xf (x)
e
x
2
dx +
1
2e
_
1
0
e
x
2
1 +x
2
dx =

8
.
R: Se constata ca f (0) = 0 si f
(x) =
e
x
2
1+x
2
. Integrand prin part i, avem:
_
1
0
xf (x)
e
x
2
dx =
1
2
f (x) e
x
2
1
0
+
1
2
_
1
0
e
x
2
f
(x) dx =

8

f (1)
2e
.
10.34 Fie f (x) =
_
x
1
x
cos t
2
dt, x > 0. Sa se calculeze f
(x).
R: f
(x) =
1
2
x
cos x +
1
x
2
cos
1
x
2
.
10.35 Sa se determine funct iile derivabile f : [0, ) R, care verica relat ia:
x +
_
x
0
f (t) dt = (x + 1) f (x) .
R: f (0) = 0 si prin derivarea relat iei date, obt inem: 1 + f (x) = [(x + 1) f (x)]
, de
unde: f
(x) =
1
x+1
. Deci f (x) = ln (1 +x).
10.36 Fara a calcula efectiv integrala, sa se arate ca:
0
_
1
0
ln
e
x
+ 1
2
dx ln
e + 1
2
.
R: Fie f (x) = ln
e
x
+1
2
. Din: f
(x) > 0 pe R, rezulta: f (0) < f (x) < f (1) etc.

10.37 Fie f : [0, 1] [a, b] o funct ie continua pe [0, 1]. Sa se arate ca daca:
_
1
0
f (x) dx = 0, atunci
_
1
0
f
2
(x) dx ab.
R: Se integreaza pe [0, 1] inegalitatea: [f (x) a] [f (x) b] 0.
10.38 Fie f : [a, b] R o funct ie derivabila, cu derivata continua, a..
f
(x) 1 +f
2
(x) , x [a, b] .
Sa se arate ca: b a < .
R: Se integreaza pe [a, b] inegalitatea:
f
(x)
1 +f
2
(x)
1, x [a, b]
si se t ine seama de faptul ca:
2
< arctg <

2
, pentru orice R.
10.39 Daca f : R R este o funct ie continua si periodica, de perioada T, atunci:
_
x+T
x
f (t) dt =
_
T
0
f (t) dt, x R.
R: Fie F : R R, denita prin F (x) =
_
x+T
x
f (t) dt. Deoarece F
(x) = f (x +T)
f (x) = 0, rezulta ca F (x) = C. Pentru x = 0 obt inem C =
_
T
0
f (t) dt.
10.40 Fie I
n
=
_
1
0
x
2n
1+x
dx. Se cere:
1) Sa se arate ca pentru orice n N are loc inegalitatea: 0 I
n

1
2n+1
.
2) Sa se calculeze lim
n
I
n
.
3) Folosind identitatea:
1 x +x
2
x
3
+ x
2n1
=
1
1 +x

x
2n
1 +x
,
sa se arate ca:
lim
n
_
1
1
2
+
1
3

1
4
+
1
2n
_
= ln 2.
10.41 Fie P (x) = a
0
+a
1
x +a
2
x
2
+ +a
n
x
n
. Sa se arate ca exista c (0, 1) a..
P (c) = a
0
+
a
1
2
+
a
2
3
+ +
a
n
n + 1
.
R: Aplicam prima formula de medie integralei
_
1
0
P (x) dx.
10.42 Fie f : [0, 1] R o funct ie continua care satisface condit ia:
6
_
1
0
f (x) dx = 2a + 3b + 6c.
Sa se arate ca exista x
0
(0, 1) a.. f (x
0
) = ax
2
0
+bx
0
+c.
R: Fie g : [0, 1] R denita prin: g (x) = 6
_
f (x) ax
2
+bx +c
. Se constata
imediat ca
_
1
0
g (x) dx = 0. Pe de alta parte, din teorema de medie, rezulta ca exista
x
0
(0, 1) a..
_
1
0
g (x) dx = g (x
0
).
10.43 Fie f : [0, 1] R o funct ie continua care satisface condit ia:
_
1
0
f (x) dx =
1
3
.
Sa se arate ca exista c (0, 1) a.. f (c) = c
2
.
R: Condit ia din enunt se mai scrie:
_
1
0
_
f (x) x
2
dx = 0 si se aplica teorema de
medie.
10.44 Fie f : [0, 1] R o funct ie derivabila, cu derivata continua pe [0, 1]. Sa se arate
ca exista c (0, 1) a..
_
1
0
f (x) dx = f (0) +
1
2
f
(c) .
R: Avem:
_
1
0
f (x) dx = (x 1) f (x)[
1
0
_
1
0
(x 1) f
(x) dx,
dar, conform formulei de medie, exista c (0, 1) a..
_
1
0
(x 1) f
(x) dx = f
(c)
_
1
0
(x 1) dx =
1
2
f
(c) .
10.45 Fie f : [0, 1] R o funct ie de doua ori derivabila, cu derivata f
continua pe
[0, 1]. Sa se arate ca exista c (0, 1) a..
_
1
0
f (x) dx = f (0) +
1
2
f
(0) +
1
6
f
(c) .
R: Se integreaza de doua ori prin part i si se aplica teorema de medie.
10.46 Sa se determine funct iile continue f : [0, ) R care verica egalitatea
sin
__
x
0
f (t) dt
_
=
x
1 +x
, x > 0.
R: Din egalitatea data rezulta:
_
x
0
f (t) dt = arcsin
x
1 +x
, de unde f (x) =
1
(1 +x)
1 + 2x
.
10.47 Fie f : [a, b] R o funct ie continua pe [a, b]. Sa se arate ca exista c (a, b)
pentru care:
a
_
c
a
f (x) dx +b
_
b
c
f (x) dx =
_
b
a
xf (x) dx.
R: Fie funct ia F : [a, b] R, denita prin: F (t) =
_
t
a
f (x) dx, derivabila cu F
(t) =
f (t), x [a, b]. Avem, succesiv:
_
b
a
xf (x) dx =
_
b
a
xF
(x) dx = xF (x)[
b
a
_
b
a
F (x) dx = b
_
b
a
f (x) dx
_
b
a
F (x) dx.
Conform teoremei de medie exista c (a, b) a..
_
b
a
F (x) dx = (b a) F (c).
10.48 Fie f : [0, 1] R o funct ie continua pe [0, 1] pentru care exista n N
a..
_
1
0
f (x) dx = 1 +
1
2
+
1
3
+ +
1
n
.
Sa se arate ca exista x
0
(0, 1) a.. f (x
0
) =
1x
n
0
1x
0
.
R: Fie g : [0, 1] R, denita prin:
g (x) = f (x)
_
1 +x +x
2
+ +x
n1
_
.
Se constata imediat ca
_
1
0
g (x) dx = 0, deci dupa teorema de medie exista x
0
(0, 1)
a.. g (x
0
) = 0.
10.3 Integrale improprii
10.49 Sa se studieze natura si n caz de convergent a sa se calculeze integralele improprii:
1) I
n
=
_

0
dx
(a
2
+x
2
)
n
, a > 0, n N
. 2) I
n
=
_
a
0
x
n
a
2
x
2
dx, a > 0, n N.
R: 1) Aplicam Criteriul I. Deoarece [f (x)[ x
2n
=
x
2n
(a
2
+x
2
)
n 1, x (0, ), cum
= 2n > 1 si M = 1, rezulta ca integrala este convergenta. Avem apoi:
I
1
=

2a
, I
n
=
1
a
2
2n 3
2 (n 1)
I
n1
, n 2.
2) Aplicam Criteriul II. Deoarece [f (x)[ (a x)
1
2
=
x
n
a+x

a
n
a
, x (0, a), cum
=
1
2
< 1 si M =
a
n
a
, rezulta ca integrala este convergenta. Avem apoi:
I
1
=

2
, I
n
= a
2
n 1
n
I
n1
, n 2.
1) I =
_

1
1
x
x
2
1
dx. 2) I =
_

a
1
x
x
2
+ 1
dx, a > 0. 3) I =
_

1
ln x
x
dx.
R: 1) Scriem integrala ca suma de doua integrale, una pe intervalul
_
1,
si a doua
pe intervalul [
2, ). Pentru prima integrala =

1
2
< 1, M =
1
2
, pentru a doua
integrala = 2 > 1, M =
2, deci ambele integrale sunt convergente. Se obt ine I =

2
.
2) Convergenta si I =
1
2
ln
a
2
+1
a
2
1
. 3) Convergenta pentru > 1 si I =
1
(1)
2
, divergenta
pentru 1.
1) I =
_

1
dx
x(x + 1)
. 2) I =
_
2
0
dx
(1 +x
2
)
4 x
2
. 3) I =
_
1
1
x 1
3
x
5
dx.
R: 1) Convergenta si I = ln 2. 2) Convergenta si I =

2
5
. 3) Divergenta.
10.52 Sa calculeze integralele:
1) I =
_
2
0
dx
4 3 cos x
. 2) I =
_

0
dx
sin
4
x + cos
4
x + sin
2
xcos
2
x
.
R: 1) Efectuam schimbarea de variabila x = +u si obt inem:
I =
_

du
4 + 3 cos u
=
_

2 dt
t
2
+ 7
=
2
7
.
2) Scriind integrala ca suma a doua integrale, una pe
_
0,

2
si a doua pe
_
2
,
cu
schimbarea de variabila t = tg x, se obt ine:
I = 2
_

0
1 +t
2
t
4
+t
2
+ 1
dt =
2
3
.
1) I
n
=
_

0
e
x
x
n
dx. 2) I =
_

0
arctg x
(1 +x
2
)
3
2
dx. 3) I =
_

0
xln x
(1 +x
2
)
3
dx.
4) I =
_
b
a
dx
_
(x a) (b x)
, a < b. 5) I =
_
1
1
ln (2 +
3
x)
3
x
dx. 6) I =
_

1
x
(1 +x)
2
dx.
7) I =
_
b
a
xdx
_
(x a) (b x)
, a < b. 8) I =
_
e
1
dx
x
ln x
. 9) I =
_
1
0
ln (1 x) dx.
R: 1) I
n
= nI
n1
, deci I
n
= n!. 2) Deoarece
arctg x
(1+x
2
)
3
2
x
3
<

2
, x(0, ), integrala
este convergenta. Integrand prin part i, obt inem: I =

2
1. 3) I =
1
8
. 4) I = .
5) I = 6 9 ln
3. 6) I =
1
4
( + 2). 7) I =

2
(a +b). 8) I = 2. 9) I = 1.
1) I =
_

0
e
x
cos (x) dx, > 0. 2) I =
_ 1
e
0
dx
xln
2
x
. 3) I =
_
5
3
x
2
dx
_
(x 3) (5 x)
.
4) I =
_
1
0
dx
1 x
2
+ 2
1 x
2
. 5) I =
_
1
1
dx
(2 x)
1 x
2
. 6) I =
_
1
0
x
2
dx
3
_
(1 x
2
)
5
.
7) I =
_

1
dx
2x +
3
x
2
+ 1 + 5
. 8) I =
_
4
2
3 + cos x
(x 2)
2
dx. 9) I =
_
2
0
ln (cos x) dx.
R: 1) I =

2
+
2
. 2) I = 1. 3) I =
33
2
. 4) I =

3
3
. 5) I =

3
.
6) Divergenta. 7) Divergenta. 8) Divergenta.
9) Efectuam schimbarea de variabila x =

2
2t si obt inem:
I = 2 ln 2
_
4
0
dt + 2
_
4
0
ln (sin t) dt + 2
_
4
0
ln (cos t) dt.
In ultima integrala efectuam schimbarea de variabila t =

2
u. Rezulta I =
2
ln 2.
10.55 Fie f : [0, ) R o funct ie continua pe [0, ) si integrala improprie ( integrala
lui Froullani):
I =
_

0
f (ax) f (bx)
x
dx, o < a < b.
1) Sa se arate ca daca exista lim
x
f (x) = k R, atunci integrala I este convergent
si I = [f (0) k] ln
b
a
.
2) Daca exista lim
x
f (x) nu este nita, dar
_
f (x) dx este convergenta pentru

orice > 0, atunci integrala I este convergenta si I = f (0) ln
b
a
.
R: 1) Pentru orice [t
1
, t
2
] [0, ) avem:
_
t
2
t
1
f (ax) f (bx)
x
dx =
_
t
2
t
1
f (ax)
x
dx
_
t
2
t
1
f (bx)
x
dx =
=
_
at
2
at
1
f (u)
u
du
_
bt
2
bt
1
f (u)
u
du = f (c
1
)
_
bt
1
at
1
du
u
f (c
2
)
_
bt
2
at
2
du
u
= [f (c
1
) f (c
2
)] ln
b
a
,
cu c
1
[at
1
, bt
1
] si c
1
[at
2
, bt
2
]. Daca t
1
0 si t
2
, atunci c
1
0 si c
2
,
deci: f (c
1
) f (0), iar f (c
2
) k.
2) Fie F : (0, ) R o primitiva a funct iei
f(x)
x
pe (0, ). Pentru orice t (0, ),
avem:
_

t
f (ax) f (bx)
x
dx =
_

at
f (u)
u
du
_

bt
f (u)
u
du = F (bt) F (at) =
=
_
bt
at
f (u)
u
du = f (c) ln
b
a
,
cu c [at, bt]. Daca t 0, atunci c 0, deci: f (c) f (0).
10.56 Folosind integrala lui Froullani, sa se calculeze:
1) I =
_

0
e
ax
e
bx
x
dx, a, b > 0. 2) I =
_

0
1
x
ln
p +qe
ax
p +qe
bx
dx, a, b, p, q > 0.
3) I =
_

0
e
a
2
x
2
e
b
2
x
2
x
dx, ab ,= 0. 4) I =
_

0
sinax sin bx
x
dx, a, b > 0.
5) I =
_

0
cos ax cos bx
x
dx, a, b > 0. 6) I =
_

0
arctg (ax) arctg (bx)
x
dx.
R: 1) I = ln
b
a
. 2) I = ln
p+q
p
ln
b
a
. 3) I = ln
b
a
.
4) I = 0. 5) I = ln
b
a
. 6) I =

2
ln
a
b
.
10.57 Sa se calculeze integrala lui Euler-Poisson: I =
_
0
e
x
2
dx.
R: Pe intervalul (1, ) avem:
_
1
e
x
2
dx <
_
1
e
x
dx =
1
e
, iar pe intervalul [0, 1]
avem o integrala denita. Deci integrala data este convergenta. Observam ca pentru
x > 0 are loc egalitatea:
_
0
xe
x
2
y
2
dy =
_
0
e
y
2
dy = I. Putem scrie succesiv:
I
2
= I
_

0
e
x
2
dx =
_

0
Ie
x
2
dx =
_

0
__

0
xe
x
2
y
2
dy
_
e
x
2
dx =
=
_

0
__

0
xe
x
2
(y
2
+1)
dx
_
dy.
Efectuand schimbarea de variabila t = x
2
_
y
2
+ 1
_
, obt inem:
I
2
=
1
2
_

0
_
1
y
2
+ 1
_

0
e
t
dt
_
dy =
1
2
_

0
dy
y
2
+ 1
=

2
.
Rezulta ca I =
2
.
10.58 Sa se calculeze integralele lui Fresnel:
I
c
=
_

0
cos x
2
dx, I
s
=
_

0
sin x
2
dx.
R: Efectuand schimbarea de variabila t = x
2
, obt inem:
I
c
=
_

0
cos t
t
dt, I
s
=
_

0
sint
t
dt,
care sunt convergente. Putem nsa scrie:
I
c
iI
s
=
_

0
_
cos x
2
i sin x
2
_
dx =
_

0
e
ix
2
dx.
Cu schimbarea de variabila ix
2
= u
2
, gasim: I
c
iI
s
=
1
2
(1 i)
_
2
, de unde:
I
c
= I
s
=
1
2
_
2
.
10.4 Integrale cu parametri
1) I (y) =
_
y
0
ln (1 +xy)
1 +x
2
dx. 2) I (m, n) =
_
1
0
x
m
ln
n
xdx.
R: 1) Deoarece:
I
(y) =
ln
_
1 +y
2
_
1 +y
2
+
_
y
0
x
(1 +xy) (1 +x
2
)
dx =
ln
_
1 +y
2
_
2 (1 +y
2
)
+
y
1 +y
2
arctg y,
prin integrare, obt inem:
I (y) =
_
y
0
_
ln
_
1 +t
2
_
2 (1 +t
2
)
+
t
1 +t
2
arctg t
_
dt =
1
2
(arctg y) ln
_
1 +y
2
_
.
2) Derivand egalitatea
_
1
0
x
m
dx =
1
m+1
de n ori n raport cu m, gasim
I (m, n) = (1)!
n!
(m+ 1)
n+1
.
1) I
n
(y) =
_

0
dx
(x
2
+y)
n+1
, y > 0, n N. 2) I (k, y) =
_

0
e
kx
sin (xy)
x
dx.
R: 1) Avem succesiv:
I
0
(y) =

2
y
, I
1
(y) =
1
2
2y
y
, . . . , I
n
(y) =
1 3 5 (2n 1)
2 4 6 (2n)

2y
n
y
.
2) Pentru k ,= 0, derivand n raport cu y si integrand de doua ori prin part i, avem:
I
(k, y) =
_

0
e
kx
cos (xy) dx =
k
k
2
+y
2
.
Deci, I (k, y) = arctg
y
k
. Pentru k = 0, avem:
I (0, y) =
_

0
sin (xy)
x
dx =
_
_
_
2
, y < 0,
0, y = 0,
2
, y > 0.
1) I (y) =
_
0
e
x
2
y
2
x
2
dx, y > 0.
2) I (y) =
_
2
0
arctg (y sinx) dx.
3) I (y) =
_
1
0
arctg (xy)
x
1x
2
dx.
4) I (y) =
_
1
0
arctg (xy)
x(1+x
2
)
dx.
R: 1) Derivand n raport cu y, avem:
I
(y) = 2
_

0
e
x
2
y
2
x
2
y
x
2
dx = 2
_

0
e
y
2
z
2
z
2
dz = 2I (y) ,
n urma schimbarii de variabila x =
y
z
. De aici rezulta: I (y) = Ce
2y
. Pentru y = 0,
obt inem C = I (0) =
2
. Deci I (y) =
2
e
2y
. 2) I (y) =

2
ln
_
y +
_
1 +y
2
_
.
3) I (y) =

2
ln
_
y +
_
1 +y
2
_
. 4) I (y) =

2
ln (1 +y).
1) I (, ) =
_
2
0
ln
_
2
sin
2
x +
2
cos
2
x
_
dx, , > 0.
2) I (y) =
_
2
0
ln
1 +y cos x
1 y cos x
dx
cos x
, [y[ < 1. 3) I (y) =
_
2
0
ln
_
y
2
sin
2
x
_
dx, y > 1.
R: 1) I (, ) = ln
+
2
. 2) I (y) = arcsin y. 3) I (y) = ln
y+
y
2
1
2
.
10.63 Sa se arate ca integrala lui Euler de spet a a doua:
(p) =
_

0
x
p1
e
x
dx, p R.
este convergenta pentru p > 0 si divergenta pentru p 0. Sa se stabileasca relat iile:
(p + 1) = p(p), pentru p > 0 si (n + 1) = n!.
R: Putem scrie:
(p) =
_
1
0
x
p1
e
x
dx +
_

1
x
p1
e
x
dx.
Prima integrala este convergenta daca 1 p < 1, adica p > 0, ind improprie de spet a a
doua, cu e
1
< x
1p
_
x
p1
e
x
_
1, pe [0, 1]. A doua integrala este convergenta pentru
orice p, deoarece lim
x
x
_
x
p1
e
x
_
= 0, p R.
10.64 Sa se arate ca integrala lui Euler de prima spet a:
B(p, q) =
_
1
0
x
p1
(1 x)
q1
dx, p, q R,
este convergenta pentru p > 0 si q > 0 si divergenta pentru p 0 sau q 0. Sa se
stabileasc a relat iile:
B(p, q) =
(p) (q)
(p +q)
, p, q > 0, B(m, n) =
(m1)! (n 1)!
(m+n 1)!
, m, n N
.
R: Putem scrie:
B(p, q) =
_ 1
2
0
x
p1
(1 x)
q1
dx +
_
1
1
2
x
p1
(1 x)
q1
dx.
Fie m
1
, M
1
marginile funct iei (1 x)
q1
pe
_
0,
1
2
. Atunci:
0 < m
1
x
1p
_
x
p1
(1 x)
q1
M
1
.
Rezulta ca prima integrala este convergenta daca p > 0, q R. Fie apoi m
2
, M
2
marginile funct iei x
p1
pe
_
1
2
, 1
. Atunci:
0 < m
2

p1
(1 x)
1q
_
x
p1
(1 x)
q1
M
2
.
Rezulta ca a doua integrala este convergenta daca q > 0, p R. Deci B(p, q) este
convergenta daca p > 0 si q > 0.
Capitolul 11
Integrale curbilinii
11.1 Lungimea unui arc de curba
11.1 Sa se calculeze lungimile urmatoarelor drumuri:
1) x = ln
_
t +
1 +t
2
_
, y =
1 +t
2
, t [0, 1] .
2) x = a cos
3
t, y = a sin
3
t, t [0, 2] .
R: 1) Avem x
(t) =
1
1+t
2
, y (t) =
t
1+t
2
, deci
L =
_
1
0
_
1
1 +t
2
+
t
2
1 +t
2
dt =
_
1
0
dt = 1.
2) Avem x
(t) = 3a cos
2
t sin t si y
(t) = 3a sin
2
t cos t, deci
L = 3a
_
2
0
[sin t cos t[ dt = 6a
_
2
0
sin 2t dt = 6a.
1) x = ln tg
t
2
, y = ln
_
1 + sin t
1 sin t
, t
_
6
,

3
_
.
2) x = 5 sin t sin 5t, y = 5 cos t cos 5t, t [0, 2] .
R: 1) Avem x
(t) =
1
sin t
, y
(t) =
1
cos t
. Atunci
L =
_
3
6
_
1
sin
2
t
+
1
cos
2
t
dt = ln 3.
2) Avem x
(t) = 5 cos t 5 cos 5t, y
(t) = 5 sin t 5 sin 5t, deci

L = 5
2
_
2
0
1 cos 3t dt = 10
_
2
0
[sin 3t[ dt = 60
_
3
0
sin 3t dt = 40.
141
CAPITOLUL 11. INTEGRALE CURBILINII 142
1) x = e
at
(a sin bt b cos bt) , y = e
at
(a cos bt +b sin bt) , t [0, 1] , a, b > 0.
2) x =
t
2
[sin (ln t) cos (ln t)] , y =
t
2
[sin (ln t) + cos (ln t)] , t [1, 2] .
3) x =
_
3t
2
6
_
sin t
_
t
3
6t
_
cos t, y =
_
3t
2
6
_
cos t +
_
t
3
6t
_
sin t,
t [2, 2] .
R: 1) L =
a
2
+b
2
a
(e
a
1). 2) L = 1. 3) L = 8
4
.
1)
_
_
_
x = t,
y =
2 ln (cos t) ,
z = tg t t,
t
_
4
,

4
_
. 2)
_
_
_
x = tg t,
y = ctg t,
z =
2 ln (tg t) ,
x
_
4
,

3
_
.
R: 1) L = 2. 2) L =
2
3
3
.
11.2 Integrale curbilinii de primul tip
11.5 Sa se calculeze integralele curbilinii de primul tip, pe arcele de curba (, indicate:
1) I =
_
C
xy ds, (() x = t, y = t
2
, t [1, 1] .
2) I =
_
C
y
2
ds, (() x =
1
4
t
4
, y = t, t [0, 2] .
3) I =
_
C
_
y (2 y) ds, (() x = t sin t, y = 1 cos t, t
_
0,

2
.
4) I =
_
C
x
2
y
2
ds, (() x = a cos
3
t, y = a sin
3
t, a > 0, t [0, 2] .
R: 1) Deoarece ds =
1 + 4t
2
dt, avem
I =
_
1
1
t
3
_
1 + 4t
2
dt = 0,
integrantul ind o funct ie impara si intervalul de integrare este simetric fat a de origine.
2) Deoarece ds =
t
6
+ 1 dt, avem
I =
_
2
0
t
2
_
t
6
+ 1 dt =
1
3
_
8
0
_
u
2
+ 1 du =
4
3
65 +
1
6
ln
_
8 +
65
_
.
3) Deoarece ds =
_
(1 cos t)
2
+ sin
2
t dt = 2 sin
t
2
dt, avem
I = 2
_
2
0
sin t sin
t
2
dt = 4
_
2
0
sin
2
t
2
cos
t
2
dt =
4
3
2
.
4) Obt inem:
I =
3a
5
2
7
_
2
0
[sin 2t[
7
dt =
3a
5
2
5
_
2
0
sin
7
2t dt,
deoarece funct ia [sin 2t[
7
este periodica, de perioada

2
. Efectuam schimbarea de variabila
u = cos 2t si obt inem:
I =
3a
5
2
6
_
1
1
_
1 u
2
_
3
du =
3
70
a
5
.
11.6 Sa se calculeze integrala curbilinie I =
_
C
_
x
2
+y
2
ds, unde ( este cercul de
ecuat ie x
2
+y
2
= ax.
R: O reprezentare parametrica a cercului ( este: x =
a
2
(1 + cos t), y =
a
2
sin t,
t [0, 2]. Se obt ine I = 2a
2
.
1) I =
_
C
_
x
2
+y
2
ds, (() x = r (cos t +t sin t) , y = r (sin t t cos t) , t [0, 2] .
2) I =
_
C
_
x
2
+y
2
_
n
ds, (() x = a cos t, y = a sin t, t [0, 2] .
3) I =
_
C
[xy[ ds, (() x = a cos t, y = b sin t, a, b > 0, t [0, 4] .
R: 1) I =
r
2
3
_
_
1 + 4
2
_
3
1
_
. 2) I = 2a
2n+1
. 3) I =
8ab(a
2
+ab+b
2
)
3(a+b)
.
1) I =
_
C
_
x
2
+y
2
_
ln z ds, (() x = e
t
cos t, y = e
t
sin t, z = e
t
, t [0, 1] .
2) I =
_
C
_
x
2
+y
2
+z
2
_
1
ds, (() x = a cos t, y = a sin t, z = bt, t [0, 2] .
3) I =
_
C
xy
2
z ds, (() x = t, y =
1
3
8t
3
, z =
1
2
t
2
, t [0, 1] .
4) I =
_
C
_
x
2
+y
2
_
z ds, (() x = t cos t, y = t sin t, z = t, t [0, 1] .
R: 1) Deoarece ds =

3e
t
dt, rezulta I =
3
9
_
2e
3
+ 1
_
. 2) I =
a
2
+b
2
ab
arctg
2b
a
. 3)
I =
5
42
. 4) I =
4
3
5
+
8
2
15
.
_
C
(x +y +z) ds, unde ( = (
1
(
2
, cu:
((
1
)
_
_
_
x = r cos t,
y = r sin t,
z = 0,
t
_
0,

2
_
, ((
2
)
_
_
_
x = 0,
y = r t,
z = t,
t [0, r] .
R: I =
_
2 +
2
_
r
2
.
_
C
_
2y
2
+z
2
ds, unde ( este cercul de
ecuat ie x
2
+y
2
+z
2
= a
2
, y = x.
R: O reprezentare parametrica a curbei este: x =
a
2
cos t, y =
a
2
cos t, z = a sin t,
t [0, 2]. Se obt ine: I = 2a
2
.
11.11 Sa se calculeze masa / rului material cu densitatea liniara (x, y) = 1 + x,
care este imaginea curbei:
(() x = t, y =
1
2
t
2
, t [0, 1] .
R: Deoarece ds =
1 +t
2
dt, avem
/=
_
1
0
(1 +t)
_
1 +t
2
dt =
7
6
2 +
1
2
ln
_
1 +
2
_
1
3
.
11.12 Sa se calculeze masele relor materiale care au densitat ile liniare si reprezentarile
parametrice urmatoare:
1) (x, y, z) =
4
2y, (() x =
3
8
t
8
, y =
1
2
t
8
, z =
11
3
t
3
, t [0, 1] .
2) (x, y, z) =
2y, (() x = t, y =
1
2
t
2
, z =
1
3
t
3
, t [0, 1] .
3) (x, y, z) = x, (() x = ch t, y = sh t, z = t, t [0, ln 2] .
R: 1) /=
3
5
+
11
100
ln 11. 2) /=
1
8
_
3
3 1 +
3
2
ln
3+2
3
3
_
.
3) /=
2
2
_
15
16
+ ln 2
_
.
11.13 Sa se calculeze masa / si centrul de greutate G ale relor materiale cu den-
sitat ile liniare si reprezent arile parametrice urmatoare:
1) (x, y) = 1, (() x = Rcos t, y = Rsin t, R > 0, t [0, ] .
2) (x, y) = 1, (() x = R(t sin t) , y = R(1 cos t) , R > 0, t [0, ] .
3) (x, y) =
y, (() x = R(t sin t) , y = R(1 cos t) , R > 0, t [0, 2] .

4) (x, y) = 1, (() x = Rcos
3
t, y = Rsin
3
t, R > 0, t
_
0,

2
.
R: 1) /= R, G
_
0,
2R
_
. 2) /= 4R, G
_
4
3
R,
4
3
R
_
.
3) /= 2R
2R, G
_
R,
3
2
R
_
. 4) /=
3
2
R, G
_
2
5
R,
2
5
R
_
.
11.14 Sa se calculeze masa / si centrul de greutate G ale relor materiale cu den-
sitat ile liniare si reprezent arile parametrice urmatoare:
1) (x, y, z) = 1, (() x = a cos t, y = a sin t, z = bt, t [0, 2] .
2) (x, y, z) =
|z|
2
, (() x = 4t
5
, y =
15 t
4
, z = 2t
3
, t [1, 1] .
R: 1) /= 2
a
2
+b
2
, G(0, 0, b). 2) /= 7, G
_
0,
68
7
15
, 0
_
.
11.3 Integrale curbilinii de tipul al doilea
11.15 Sa se calculeze integralele curbilinii de tipul al doilea, pe arcele de curba (, indi-
cate:
1) I =
_
C
xy dx y
2
dy, (() x = t
2
, y = t
3
, t [0, 1] .
2) I =
_
C
1 x
2
dx +xdy, (() x = cos t, y = 2 sin t, t
_
2
,

2
.
3) I =
_
C
ye
x
dx, (() x = ln
_
1 +t
2
_
, y = 2arctg t t, t [0, 1] .
4) I =
_
C
x
2
y dy xy
2
dx, (() x =
cos t, y =
sin t, t
_
0,

2
.
R: 1) Deoarece: dx = 2t dt, dy = 3t
2
dt, avem: I =
_
1
0
_
2t
6
3t
8
_
dt =
1
21
.
2) Deoarece: dx = sint, dy = 2 cos t dt, obt inem I = . 3) I =
8
3
. 4) I =

4
.
11.16 Sa se calculeze integralele curbilinii de tipul al doilea:
1) I =
_
C
x
2
dyy
2
dx
x
3
x
2
+y
3
y
2
, (()
_
x = r cos
3
t,
y = r sin
3
t,
t
_
0,

2
.
2) I =
_
C
(arcsin y) dx +x
3
dy, (()
_
x = t,
y =
1 t
2
,
t [1, 1] .
R: 1) I =
3
16
r
3
r. 2) I =
3
8
2.
11.17 Sa se calculeze integrala curbilinie de tipul al doilea I =
_
C
(x +y) dx(x y) dy,
unde ( este curba simpla, nchis a si orientata pozitiv, care are drept imagine triunghiul
cu varfurile n punctele O(0, 0), A(1, 1), B(0, 2) si ambele capete n origine.
R: Avem: ( = (
1
(
2
(
3
, cu: ((
1
) x = t, y = t, t [0, 1], ((
2
) x = 2 t, y =
t, t [1, 2], ((
3
) x = 0, y = 2 t, t [0, 2].

Incat: I =
_
1
0
2t dt +
_
2
1
(4 + 2t) dt +
_
2
0
(2 +t) dt = 2.
_
C
2xdy 3y dx, unde
( este curba simpla, nchisa si orientata pozitiv, care are drept imagine dreptunghiul cu
varfurile n punctele A(1, 2), B(3, 1), C (2, 5) si ambele capete n punctul A.
R: I =
35
2
.
11.19 Sa se calculeze integrala curbilinie de tipul al doilea
I =
_
C
dx +dy
max [x[ , [y[
,
unde ( este curba simpla, nchis a si orientata pozitiv, care are drept imagine triunghiul
cu varfurile n punctele A(1, 1), B(2, 1), C (2, 1), D(1, 1) si ambele capete n
punctul A.
R: I = 1.
_
C
ydx(x a) dy, unde
( este curba simpla, nchisa si orientata pozitiv, care are drept imagine elipsa:
(x a)
2
a
2
+
y
2
b
2
= 1, a, b > 0
si ambele extremitat i n origine.
R: O reprezentare parametrica a curbei ( este: x = a (1 + cos t), y = b sin t, t
[, ]. Se obt ine I = 2ab.
_
C
_
x
2
y
2
_
dx, unde (
este arcul din parabola y = x
2
cuprins ntre punctele O(0, 0) si A(2, 4).
R: I =
56
15
.
_
C
_
x y
2
_
dx +2xy dy,
unde ( este curba simpla, nchis a si orientata pozitiv, care are drept imagine conturul
domeniului plan delimitat de curbele: y
2
= 8x, 9x
2
+ y
2
= 1 si y = 0, situat n primul
cadran.
R: Varfurile conturului sunt: O(0, 0), A
_
1
3
, 0
_
, B
_
1
9
,
2
2
3
_
. Se obt ine I =
80
243
.
cate:
1) I =
_
C
y dx xdy +
_
x
2
+y
2
+z
2
_
dz, (()
_
_
_
x = t cos t + sin t,
y = t sin t + cos t,
z = t + 1,
t [0, ] .
2) I =
_
C
(y z) dx + (z x) dy + (x y) dz, (()
_
_
_
x = a cos t,
y = a sin t,
z = bt,
t [0, 2] .
R: 1) Deoarece: dx = t sin t dt, dy = t cos t dt, dz = dt, x
2
+y
2
+z
2
= 2t
2
+2t +2, se
obt ine I =
3
+
2
+ 2. 2) I = 2a (a +b).
cate:
1) I =
_
C
xdx +xy dy +xyz dz, (() x = e
t
, y = e
t
, z =
2 t, t [0, 1] .
2) I =
_
C
z
a
2
x
2
dx +xz dy +
_
x
2
+y
2
_
dz, (()
_
_
_
x = a cos t,
y = a sin t,
z = bt,
t
_
0,

2
.
R: 1) I =
1
2
e
2
+
1
e

1
2
. 2) I =
a
2
b
2
( 1).
I =
_
C
_
y
2
+z
2
dx +
_
z
2
+x
2
dy +
_
x
2
+y
2
dz,
unde ( este curba simpla care are drept imagine segmentul [AB] cu: A(1, 1, 1) si
B(2, 2, 2), iar primul capat n A.
R: I =
15
2
2
.
I =
_
C
(y 2z) dx (z x) dy + (2x y) dz,
unde ( este curba simpla de ecuat ii: (()
_
x
2
+y
2
+z
2
= a
2
,
x y +z = 0,
cu a > 0 si ambele capete
n punctul A
_
a
2
, 0,
a
2
_
.
R: O reprezentare parametrica a curbei ( este:
(() x =
a
2
cos t +
a
6
sin t, y =
2a
6
sin t, z =
a
6
sint
a
2
cos t, t [0, 2] .
Se obt ine I =
4a
2
3
.
11.4 Independent a de drum a integralelor curbilinii
11.27 Constatand n prealabil ca expresia de sub semnul integrala este o diferent iala ex-
acta, sa se calculeze urmatoarele integrale curbilinii, n care s-au specicat numai capetele
curbei de integrare:
1) I =
(1,3)
_
(2,1)
y dx +xdy. 2) I =
(2,0)
_
(0,2)
y
2
e
x
dx + 2ye
x
dy.
3) I =
(2,3)
_
(1,1)
(x + 3y) dx + (3x +y) dy. 4) I =
(2,1)
_
(0,0)
2xy dx +x
2
dy.
R: 1) Cum P (x, y) = y, Q(x, y) = x si
P
x
=
Q
y
= 1, rezulta ca valoarea integralei
nu depinde de curba recticabila cu capetele n punctele (2, 1) si (1, 3). Fie A
1
(2, 1),
A
2
(1, 1) si A
3
(3, 1). Alegem pentru integrare curba simpla ( = (
1
(
2
, n care (
1
are
ca imagine segmentul A
1
A
2
paralel cu axa Ox, iar (
2
are ca imagine segmentul A
2
A
3
paralel cu axa Oy, avand reprezentarile parametrice:
((
1
)
_
x = t,
y = 1,
t [2, 1] , ((
2
)
_
x = 1,
y = t,
t [1, 3] .
Obt inem: I =
_
C
y dx+xdy =
_
C
1
y dx+xdy +
_
C
2
y dx+xdy =
_
1
2
dt +
_
3
1
dt = 1. Se
observa usor ca funct ia U (x, y) = xy este o primitiva a expresiei diferent iale y dx+xdy,
adica dU = dx +xdy si deci I = U (1, 3) U (2, 1) = 1.
2) I = 4. 3) I =
41
2
. 4) I = 4.
1) I =
(5,12)
_
(3,4)
x dx+y dy
x
2
+y
2
. 2) I =
(9,1)
_
(
1
2
,2)
1
2
_
y
x
dx +
1
2
_
x
y
dy.
3) I =
(3,2)
_
(1,2)
y
2
(xy)
2
dx
x
2
(xy)
2
dy. 4) I =
(3,0)
_
(
1
3
,2)
y
1+xy
dx +
x
1+xy
dy.
R: 1) I = ln
13
5
. 2) I = 2. 3) I = 4. 4) I = ln 3.
1) I =
(2,3,1)
_
(1,1,0)
yz dx +xz dy +xy dz. 2) I =
(2,1,3)
_
(1,1,2)
xdx y
2
dy +z dz.
3) I =
(3,4,5)
_
(0,0,0)
x dx+y dy+z dz
x
2
+y
2
+z
2
. 4) I =
(0,3,4)
_
(1,2,2)
x dx+y dy+z dz
(x
2
+y
2
+z
2
)
3
2
.
R: 1) Cum: P (x, y, z) = yz, Q(x, y, z) = xz, R(x, y, z) = xy, avem:
R
y
=
Q
z
= x,
P
z
=
R
x
= y,
Q
x
=
P
y
= z,
deci expresia de sub semnul integrala este o diferent iala exacta si integrala curbilinie nu
depinde de drum. Fie A
1
(1, 1, 0), A
2
(2, 1, 0), A
3
(2, 3, 0), A
4
(2, 3, 1). Alegem pentru
integrare curba simpla ( = (
1
(
2
(
3
, n care (
1
1
A
2
paralel
cu axa Ox, (
2
2
A
3
paralel cu axa Oy, (
3
are ca imagine
segmentul A
3
A
4
paralel cu axa Oy, avand reprezentarile parametrice:
((
1
)
_
_
_
x = t,
y = 1,
z = 0,
t [1, 2] , ((
2
)
_
_
_
x = 2,
y = t,
z = 0,
t [1, 3] , ((
3
)
_
_
_
x = 2,
y = 3,
z = t,
t [0, 1] .
Obt inem: I =
_
2
1
0 dt +
_
3
1
0 dt +
_
1
0
6 dt = 6. 2) I =
10
3
. 3) I = 5
2. 4) I =
2
15
.
1) I =
(5,3,1)
_
(7,2,3)
yz dx+zx dy+xy dz
(xyz)
2
. 2) I =
(2,2,2)
_
(1,1,1)
y
2
z
2
dx+2x
2
z dy+2x
2
y dz
(2x+yz)
2
.
3) I =
(2,6,3)
_
(1,3,1)
y
z
dx +
x
z
dy
xy
z
2
dz. 4) I =
(2,2,4)
_
(1,1,5)
z (dx+dy)(x+y)dz
x
2
+y
2
+z
2
+2xy
.
R: 1)I =
9
2
. 2) I =
2
3
. 3) I = 7. 4) I =

2
.
11.5 Calculul ariei cu ajutorul integralei curbilinii
11.31 Sa se calculeze, cu ajutorul integralei curbilinii, aria domeniului plan marginit
de:
1) Elipsa: x = a cos t, y = b sin t, t [0, 2].
2) Astroida: x = a cos
3
t, y = a sin
3
t, t [0, 2).
3) Cardioida: x = a (2 cos t cos 2t), y = a (2 sin t sin 2t), t [0, 2].
4) Foliul lui Descartes: x =
3at
1+t
3
, y =
3at
2
1+t
3
, t (0, ).
R: 1) Deoarece xdy y dx = ab dt, avem / =
1
2
_
2
0
ab dt = ab.
2) Deoarece xdy y dx =
3a
4
sin
2
2t dt, avem / =
3a
2
8
_
2
0
sin
2
2t dt =
3a
2
8
. 3)
/ = 6a
2
. 4) / =
3a
2
2
.
Capitolul 12
Integrale multiple
12.1 Integrala dubla
12.1 Sa se calculeze integralele duble:
1) I =
__
D
ln (x +y) dxdy, unde D = (x, y) , 0 x 1, 1 y 2 .
2) I =
__
D
cos y
1+sin x sin y
dxdy, unde D =
_
(x, y) , 0 x

2
, 0 y

2
_
.
3) I =
__
D
_
cos
2
x + sin
2
y
_
dxdy, unde D =
_
(x, y) , 0 x

4
, 0 y

4
_
.
4) I =
__
D
e
x+sin y
cos y dxdy, unde D = [0, ]
_
0,

2
.
5) I =
__
D
x
2
1+y
2
dxdy, unde D = [0, 1] [0, 1] .
R: 1) Funct ia de sub semnul integrala este continua. Domeniul D este un dreptunghi.
Aplicam formula de reducere la integrale iterate, n ordinea y, x. Avem:
I =
_
1
0
dx
_
2
1
ln (x +y) dy =
_
1
0
[(x + 2) ln (x + 2) (x + 1) ln (x + 1) 1] dx,
deci I =
9
2
ln 3 4 ln 2
3
2
.
2) Domeniul D este un dreptunghi. Aplicam formula de reducere la integrale iterate,
n ordinea x, y. Avem mai ntai, efectuand schimbarea de variabila t = tg
x
2
:
_
2
0
cos y
1 + sin xsin y
dx =
_
1
0
2 cos y dt
t
2
+ 2t sin y + 1
= 2arctg
1 + sin y
cos y
2y =

2
y.
Apoi,
_
2
0
dy
_
2
0
cos y
1 + sin xsin y
dx =
_
2
0
_
2
y
_
dy =
1
8
2
.
3) I =
_
4
0
dx
_
4
0
_
cos
2
x + sin
2
y
_
dy =
1
16
2
. 4) I = (e 1) (e
1). 5) I =

12
.
12.2 Sa se calculeze integralalele iterate:
1) I =
_
1
0
dx
_
1
0
_
x
3
+ 2xy
_
dy. 2) I =
_
2
1
dx
_
1
0
1
x+y
dy.
3) I =
_
1
1
dx
_
1
0
y
1+x
2
y
2
dy. 4) I =
_
1
0
dx
_
1
0
x
2
1+y
2
dy.
R: 1) I =
3
4
. 2) I = 3 ln 3 4 ln 2. 3) I =
1
2
ln 2. 4) I =
1
12
.
149
CAPITOLUL 12. INTEGRALE MULTIPLE 150
1) I =
__
D
y dxdy
(1+x
2
+y
2
)
3
2
, unde D = [0, 1] [0, 1] .
2) I =
__
D
x
2
y cos
_
xy
2
_
dxdy, unde D =
_
0,

2
[0, 2] .
3) I =
__
D
x
2
ye
xy
dxdy, unde D = [0, 1] [0, 2] .
4) I =
__
D
dxdy
(x+y+1)
2
, unde D = [0, 1] [0, 1.
R: 1) I = ln
2+
2
1+
3
. 2) I =
16
. 3) I = 2. 4) I = ln
4
3
.
12.4 Sa se transforme integrala dubla I =
__
D
f (x, y) dxdy n integrale simple iterate,
pentru urmatoarele domenii:
1) D =
_
(x, y) , x
2
+y
2
2x
_
.
2) D =
_
(x, y) , x
2
+y
2
4, x
2
+
1
4
y
2
1, x 0
_
.
R: 1) D este un domeniu simplu n raport cu axa Oy:
D = (x, y),
_
2x x
2
y
_
2x x
2
, x [0, 2],
deci I =
_
2
0
dx
_
2xx
2
2xx
2
f (x, y) dy.
2) D este un domeniu simplu n raport cu axa Ox:
D = (x, y),
_
1
1
4
y
2
x
_
4 y
2
, y [2, 2],
deci I =
_
2
2
dy
_
4y
2
1
1
4
y
2
f (x, y) dx.
12.5 Sa se calculeze urmatoarele integrale iterate:
1) I =
_
1
1
dx
_
x
x
xdy. 2) I =
_
1
0
dx
_

x
x
2
xy dy. 3) I =
_
R
R
dy
_

R
2
y
2
R
2
y
2
3x
2
y
2
dx.
R: 1) I =
4
3
. 2) I =
4
27
. 3) I = 2R
6
_
2
2
sin
2
t cos
4
t dt =

8
R
6
.
12.6 Sa se calculeze integrala dubla: I =
__
D
(x y) dxdy, unde D este domeniul plan
marginit de curbele de ecuat ii: y = 2 x
2
si y = 2x 1.
R: I =
64
15
.
12.7 Sa se calculeze integralele duble pe domeniul D marginit de curbele indicate:
1) I =
__
D
(x + 2y) dxdy, y = x, y = 2x, x = 2, x = 3.
2) I =
__
D
_
x
2
+y
2
_
dxdy, y = x, x = 0, y = 1, y = 2.
3) I =
__
D
_
3x
2
2xy +y
_
dxdy, x = 0, x = y
2
, y = 2.
4) I =
__
D
y ln xdxdy, xy = 1, y =
x, x = 2.
5) I =
__
D
(cos 2x + sin y) dxdy, x = 0, y = 0, 4x + 4y = .
R: 1) I =
76
3
. 2) I = 5. 3) I =
244
21
. 4) I =
5
8
(ln 4 1). 5) I =
1
4
_
+ 1 2
2
_
.
12.8 Sa se calculeze integralele duble pe domeniul D, unde D este interiorul triunghiului
cu varfurile n punctele indicate:
1) I =
__
D
xdxdy, A(2, 3) , B(7, 2) , C (4, 5) .
2) I =
__
D
_
4x
2
y
2
dxdy, O(0, 0) , A(1, 0) , B(1, 1) .
R: 1) I = 26. 2) I =
1
3
_
3
+
3
2
_
.
1) I =
__
D
(1 y) dxdy, unde D =
_
(x, y) , x
2
+ (y 1)
2
1, y x
2
, x 0
_
.
2) I =
__
D
([x[ +[y[) dxdy, unde D = (x, y) , [x[ +[y[ 1 .
3) I =
__
D
dxdy
x
, unde D =
_
(x, y) , y
2
8x, y 2x, y + 4x 24
_
.
R: 1) I =
1
15
. 2) I =
4
3
. 3) I = 15
2.
12.10 Sa se calculeze integralele duble pe domeniul D marginit de curbele indicate:
1) I =
__
D
(x +y) dxdy, y = x
2
, y = x.
2) I =
__
D
x
2
dxdy
x
2
+y
2
, x = 0, y = 1, y =
3
2, y = x.
3) I =
__
D
arcsin
x +y dxdy, x +y = 0, x +y = 1, y = 1, y = 1.
4) I =
__
D
x
3
y
dxdy, y = 4, y = x
2
, y =
1
4
x
2
.
R: 1) I =
3
20
. 2) I =
1
6
_
2 ln
_
1 +
2
_
. 3) I =

4
. 4) I = 30.
I =
_ _
D
dxdy
1 +y cos x
, unde D =
_
0,

2
_
[0, ]
si apoi sa se deduc a valoarea integralei:
J () =
_

0
ln (1 +cos x)
cos x
dx, (0, 1) .
R: Integrand n ordinea y, x, avem:
I =
_
2
0
dx
_

0
dy
1 +y cos x
=
_

0
ln (1 +cos x)
cos x
dx = J () .
Schimband ordinea de integrare si punand tg
x
2
= t, y = cos 2, obt inem:
I =
_

0
dy
_
2
0
dx
1 +y cos x
= 2
_ 1
2
arccos
4
sin 2 d
_
1
0
2
sin 2
d (ttg )
1 +t
2
tg
2
,
de unde, I = J () =

2
8

1
2
(arccos )
2
.
12.12 Sa se calculeze aria domeniului plan marginit de parabolele: y
2
= 10x + 26 si
y
2
= 10 6x.
R: Parabolele se intersecteazan punctele: (1, 4) si (1, 4). Considerand domeniul
simplu n raport cu aza Ox, putem scrie:
D =
_
(x, y) ,
y
2
26
10
x
10 y
2
6
, y [4, 4]
_
,
deci / =
__
D
dxdy =
_
4
4
dy
_
10y
2
6
y
2
26
10
dx =
1024
45
.
12.13 Sa se calculeze aria domeniului plan marginit de elipsa
x
2
a
2
+
y
2
b
2
= 1.
R: Considerand domeniul simplu n raport cu axa Oy, avem
D =
_
(x, y) ,
b
a
_
a
2
x
2
y
b
a
_
a
2
x
2
, x [a, a]
_
,
deci
/ =
_ _
D
dxdy =
_
a
a
dx
_ b
a
a
2
x
2
b
a
a
2
x
2
dy = 2
b
a
_
a
a
_
a
2
x
2
dx = ab.
12.14 Sa se calculeze aria domeniului plan marginit de curbele de ecuat ii x = y
2
2y,
x +y = 0.
R: / =
1
6
.
12.15 Sa se calculeze volumul corpului marginit de planele de coordonate, planul x+y =
1 si paraboloidul eliptic z = 2x
2
+y
2
+ 1.
R: D = (x, y) , 0 y 1 x, x [0, 1] si deci:
1 =
_ _
D
(2x
2
+y
2
+ 1) dxdy =
_
1
0
dx
_
1x
0
(2x
2
+y
2
+ 1) dy =
3
4
.
12.16 Sa se calculeze volumul corpului marginit de planele x = 1, z = 0 si paraboloidul
hiperbolic z = x
2
y
2
.
R: D = (x, y) , x y x, x [0, 1] si deci
1 =
_ _
D
(x
2
y
2
) dxdy =
_
1
0
dx
_
x
x
(x
2
y
2
)dy =
1
3
.
12.17 Sa se calculeze volumul corpului marginit de planele y = x, y = 0, z = 0 si
cilindrul x
2
+z
2
= a
2
, situat n primul octant.
R: 1 =
_
a
0
dx
_
x
0
a
2
x
2
dy =
1
3
a
3
.
12.18 Sa se calculeze volumul corpului marginit de elipsoidul
x
2
a
2
+
y
2
b
2
+
z
2
c
2
= 1.
R: 1 = 8
_
a
0
dx
_ b
1
x
2
a
2
0
c
_
1
x
2
a
2

y
2
b
2
dy =
4
3
abc.
12.19 Sa se calculeze, trecand la coordonate polare, urmatoarele integrale duble:
1) I =
__
D
_
x
2
+y
2
dxdy, unde D =
_
(x, y) , x
2
+y
2
4
_
.
2) I =
__
D
sin
_
x
2
+y
2
_
dxdy, unde D =
_
(x, y) , x
2
+y
2
a
2
, x 0
_
.
3) I =
__
D
_
a
2
x
2
y
2
dxdy, unde D =
_
(x, y) , x
2
+y
2
ax
_
.
4) I =
__
D
_
x
2
+y
2
dxdy, unde D =
_
(x, y) , ax x
2
+y
2
2ax
_
.
R: 1) Trecand la coordonate polare x = r cos , y = r sin , cum J (r, ) = r, avem:
I =
_ _
D
r
2
drd, unde D
= (r, ) , 0 r 2, [0, 2]
si deci: I =
_
2
0
dr
_
2
0
r
2
d =
16
3
. 2) I =
_
a
0
dr
_ 3
2
2
r sin r
2
d =
1
2
_
1 cos a
2
_
.
3) Trecand la coordonate polare avem:
I =
_ _
D
r
_
a
2
r
2
drd, unde D
=
_
(r, ) , 0 r a cos ,
_
2
,

2
__
si deci:
I = 2
_
2
0
d
_
a cos
0
r
_
a
2
r
2
dr =
2
3
a
3
_
2
0
_
1 sin
3
_
d =
1
9
a
3
(3 4) .
4) Trecand la coordonate polare avem:
I =
_
2
0
d
_
2a cos
a cos
r
2
dr =
7
3
a
3
_
2
0
cos
3
d =
14
9
a
3
.
12.20 Sa se calculeze integrala I pe domeniul D marginit de curbele de ecuat ii indicate:
1) I =
__
D
sin
x
2
+y
2
x
2
+y
2
dxdy, x
2
+y
2
=

2
9
, x
2
+y
2
=
2
.
2) I =
__
D
dxdy, xy = 1, xy = 2, y = x, y = 3x.
R: 1) Trecand la coordonate polare avem: D
=
_
3
,
[0, 2] si deci:
I =
_ _
D
sinr drd =
_
2
0
d
_

3
sin r dr = 3.
2) Efectuam schimbarea de variabile: x =
_
u
v
, y =

uv, avem: J (u, v) =
1
2v
.
Rezulta I = ln
3.
12.21 Sa se calculeze aria domeniului plan marginit de curbele de ecuat ii: xy = a,
xy = b (0 < a < b), y = x, y = x (0 < < ) si situat n primul cadran.
R: Efectuam schimbarea de variabile: u = xy, v =
y
x
, D
= [a, b] [, ]. Deoarece
J (u, v) =
1
2v
, avem:
/ =
_ _
D
dxdy =
_ _
D
1
v
dudv =
b a
2
ln

.
12.22 Sa se calculeze aria domeniului plan marginit de curbele de ecuat ii: xy = a,
xy = b (0 < a < b), x
2
= y, x
2
= y (0 < < ).
R: / =
ba
3
ln

.
12.23 Sa se calculeze integralele duble urmatoare, efectuand schimbari de variabile co-
respunz atoare:
1) I =
__
D
_
1
x
2
a
2

y
2
b
2
dxdy, unde D =
_
(x, y) ,
x
2
a
2
+
y
2
b
2
1
_
.
2) I =
__
D
_
(x
2
+y
2
)
3
dxdy, unde D =
_
(x, y) , x
2
+y
2
a
2
, y 0
_
.
3) I =
__
D
_
x
2
+y
2
dxdy, unde D =
_
(x, y) ,
2
x
2
+y
2
4
2
_
.
4) I =
__
D
_
x
2
+y
2
dxdy, unde D =
_
(x, y) , ax x
2
+y
2
a
2
, x 0, y 0
_
.
5) I =
__
D
_
x
2
+y
2
dxdy, unde D =
_
(x, y) , ax x
2
+y
2
2ax, y 0
_
.
R: 1) I =
2
3
ab. 2) I =
1
5
a
5
. 3) I =
14
3

4
. 4) I =
a
3
3
_
2

2
3
_
. 5) I =
14
9
a
3
.
12.24 Sa se calculeze integralele duble urmatoare, efectuand schimbari de variabile co-
respunz atoare:
1) I =
__
D
ln(x
2
+y
2
)
x
2
+y
2
dxdy, unde D =
_
(x, y) , 1 x
2
+y
2
e
2
_
.
2) I =
__
D
e
(x
2
+y
2
)
dxdy, unde D =
_
(x, y) , x
2
+y
2
4
_
.
3) I =
__
D
_
4 x
2
y
2
dxdy, unde D =
_
(x, y) , 1 x
2
+y
2
4
_
.
4) I =
__
D
ln
_
x
2
+y
2
_
dxdy, unde D =
_
(x, y) , e
2
x
2
+y
2
e
4
_
.
R: 1) I = 2. 2) I =
_
1
1
e
4
_
. 3) I = 2
3. 4) I = e
2
_
3e
2
1
_
.
12.25 Sa se calculeze urmatoarele integrale duble:
1) I =
__
D
arcsin
x
2
+y
2
2
dxdy, unde D =
_
(x, y) ,
2
x
2
+y
2
4
2
_
.
2) I =
__
D
(x
2
+y
2
)dxdy
4(x
2
+y
2
)
2
, unde D =
_
(x, y) ,
1
2
x
2
+y
2
1
_
.
R: 1) I =
3
_
7
3

1
2
3
_
. 2) Trecand la coordonate polare, avem:
D
=
_
(r, ) , 0 r
_
2
1 + sin
2
, 0 2
_
si deci I =
__
D
r
3
4r
4
drd = 4arctg
2 ln 3.
12.26 Sa se calculeze volumul corpului limitat de suprafet ele de ecuat ii z
2
= xy,

x +
y = 1, z = 0.
R: Daca D =
_
(x, y) ,

x +
y 1
_
, atunci 1 =
__
D
xy dxdy. Efectuand schim-

barea de variabile: x = u
2
, y = v
2
, (u, v) , cu
= (u, v) , 0 u 1 v, 0 v 1 ,
cum J (u, v) = 4uv, gasim: 1 =
4
3
_
1
0
v
2
(1 v)
3
dv =
1
45
.
12.27 Sa se determine masa si coordonatele centrului de greutate ale placii plane omo-
gene ( (x, y) = const.), care ocup a domeniul:
1) D =
_
(x, y) ,
x
2
a
2
+
y
2
b
2
1, x 0, y 0
_
.
2) D =
_
(x, y) , x
2
+y
2
a
2
, x
2
+y
2
ax, y 0
_
, a > 0.
R: 1) /=
1
3
a
2
b, G
_
4a
3
,
4b
3
_
. 2) /=
3
8
a
2
, G
_
a
6
,
14a
9
_
.
12.28 Sa se determine coordonatele centrelor de greutate ale placilor plane omogene
marginite de urmatoarele curbe:
1) y
2
= 4x + 4, y
2
= 2x + 4.
2) 9x
2
+ 25y
2
225 = 0, 3x + 5y = 15, x 0, y 0.
R: 1) G
_
2
5
, 0
_
. 2) G
_
10
3(2)
,
2
2
_
.
12.29 Sa se determine coordonatele centrului de greutate ale placii plane de densitate
supercial a (x, y) = y, marginita de curbele: y = x
2
si y = 1.
R: G
_
0,
5
7
_
.
12.30 Sa se calculeze momentele de inert ie n raport cu axele de coordonate si n raport
cu originea ale placii plane de densitate superciala (x, y) = xy, care ocupa domeniul
D = (x, y) , x +y 1, x 0, y 0 .
R: I
x
= I
y
=
1
120
, I
0
=
1
60
.
12.31 Sa se calculeze momentele de inert ie n raport cu axele de coordonate si n ra-
port cu originea ale placilor plane omogene, care ocupa domeniile plane marginite de
urmatoarele curbe:
1) y = x
2
, x = y
2
.
2) x
2
+y
2
= ay, a > 0.
3)
x +
y =
a, x = 0, y = 0, a > 0.
R: 1) I
x
= I
y
=
3
35
, I
0
=
6
35
. 2) I
x
=
5
64
a
4
, I
y
=
1
64
a
4
, I
0
=
3
32
a
4
. 3)
I
x
= I
y
=
1
84
a
4
, I
0
=
1
42
a
4
.
12.32 Sa se calculeze momentul de inert ie n raport cu axa Oy a placii plane de densi-
tate superciala (x, y) =
1
x
4
, care ocupa domeniul marginit de curbele de ecuat ii:
x +
y = a,
x +
y = b, x =
2
y, x =
2
y, 0 < a < b, 0 < < .
R: Efectuam schimbarea de variabile:

x+
y = u,
x
y
= v, D
= [a, b]
_
2
,
2
. Se
obt ine I
y
= 2
2
ln
b
a
.
12.33 Utilizand formula lui Green, sa se calculeze urmatoarele integrale curbilinii, pe
curbele nchise (, parcurse n sens direct:
1) I =
_
C
_
x
2
+y
2
dx + y
_
xy + ln
_
x +
_
x
2
+y
2
__
dy, unde ( este conturul drep-
tunghiului D = [1, 4] [0, 2].
2) I =
_
C
e
x
2
+y
2
(y dx +xdy), unde ( este cercul x
2
+y
2
= 1.
3) I =
_
C
(xy y) dx + (xy +x) dy, unde ( este frontiera domeniului plan
D =
_
(x, y) ,
x
2
a
2
+
y
2
b
2
1
_
, a > 0, b > 0.
4) I =
_
C
(x y) dx +dy, unde ( este frontiera domeniului plan
D =
_
(x, y) , x
2
+y
2
2x, y 0
_
.
5) I =
_
C
y
2
dx +x
2
dy, unde ( este frontiera domeniului plan
D =
_
(x, y) , x
2
+y
2
1, y 0
_
.
6) I =
_
C
_
x
2
+y
2
dx +y
_
xy + ln
_
x +
_
x
2
+y
2
__
dy, unde
(() x = 1 + cos t, y = 1 + sin t, t [0, 2].
7) I =
_
C
2
_
x
2
+y
2
_
dx + (x +y)
2
dy, unde ( este conturul triunghiului cu varfurile
n punctele A(1, 1), B(2, 2), C (1, 3).
8) I =
_
C
y
3
dx + x
3
dy, unde ( este conturul cercului cu centrul n origine si raza
egal a cu 1.
9) I =
_
C
e
x
2
+y
2
[cos (2xy) dx + sin (2xy) dy], unde (()
x
2
a
2
+
y
2
b
2
1 = 0.
R: 1) Deoarece: P (x, y) =
_
x
2
+y
2
si Q(x, y) = y
_
xy + ln
_
x +
_
x
2
+y
2
__
,
obt inem: I =
__
D
y
2
dxdy = 8. 2) I = 2e. 3) I = 2ab. 4) I =
1
2
. 5) I =
4
3
.
6) I =
5
4
. 7) I =
4
3
. 8) I =
3
2
. 9) I = 0.
12.2 Aria suprafet elor
12.34 Sa se determine aria port iunii din sfera (o) x
2
+y
2
+z
2
= a
2
, a > 0, situata n
interiorul cilindrului x
2
+y
2
= ay.
R: Datorita simetriei, aria ceruta este de patru ori aria port iunii situata n primul
octant, pentru care avem:
f (x, y) =
_
a
2
x
2
y
2
, p =
f
x
=
x
_
a
2
x
2
y
2
, q =
f
y
=
y
_
a
2
x
2
y
2
,
denita pe D
_
(x, y) , x
2
+y
2
a
2
, x 0, y 0
_
. Deci S = 4a
__
D
dxdy
a
2
x
2
y
2
. Tre-
cand la coordonate polare, avem: D
=
_
(r, ) , 0 r a sin , 0

2
_
. Se obt ine
S = 2a
2
( 2).
12.35 Sa se determine aria port iunii din conul (o) z =
_
x
2
+y
2
, situata n interiorul
cilindrului de ecuat ie: x
2
+y
2
= 2x.
R: S =
__
S
dS =
__
D
_
1 +p
2
+q
2
dxdy =
2
__
D
dxdy =
2.
12.36 Sa se calculeze aria suprafet ei:
(o) x = tg ucos v, y = tg usin v, z =
sin u
2 cos
2
u
+
1
2
ln
1 + sin u
cos u
+v,
(u, v) =
_
0,

4
[0, 2].
R: S =
__
A
2
+B
2
+C
2
dudv =
8
3
.
12.37 Sa se calculeze aria port iunii din paraboloidul de rotat ie (o) z = x
2
+y
2
, situata
n interiorul cilindrului: x
2
+y
2
= r
2
.
R: S =
__
D
_
1 + 4x
2
+ 4y
2
dxdy =

6
_
_
(4r
2
+ 1)
3
1
_
.
12.38 Sa se gaseasca aria port iunii din paraboloidul eliptic (o) z =
x
2
2a
+
y
2
2b
, a > 0,
b > 0, situata n interiorul cilindrului eliptic:
x
2
a
2
+
y
2
b
2
= c
2
.
R: S =
2
3
ab
__
1 +c
2
_
1 +c
2
1
.
12.39 Sa se calculeze aria port iunii din cilindrul parabolic (o) x
2
= 2z, marginita de
planele de ecuat ii: x = 2y, y = 2x, x = 2
2.
R: S = 13.
12.40 Sa se gaseasca aria port iunii din paraboloidul hiperbolic (o) x = 1 y
2
z
2
,
situata n interiorul cilindrului de ecuat ie: y
2
+z
2
= 1.
R: Proiectam suprafat a n planul Oyz:
S =
_ _
D
_
1 + 4y
2
+ 4z
2
dydz =
1
6
_
5
5 1
_
.
12.41 Sa se calculeze aria port iunii din cilindrul parabolic (o) z = x
2
, marginita de
planele de ecuat ii: x +y =
2, x = 0, y = 0.
R: S =
5
6
+
2
4
ln
_
3 + 2
2
_
.
12.42 Sa se calculeze aria port iunii din cilindrul (o) x
2
+z
2
= a
2
, situata n interiorul
cilindrului de ecuat ie: x
2
+y
2
= a
2
.
R: Datorita simetriei, aria cautata este de opt ori aria port iunii din primul octant, de
ecuat ie: z =
a
2
x
2
, denita pe domeniul D =
_
(x, y) , x
2
+y
2
a
2
, x 0, y 0
_
,
S = 8a
_ _
D
dxdy
a
2
x
2
= 8a
2
_
2
0
1 cos
sin
2
d = 16a
2
.
12.3 Integrala de suprafat a de primul tip
12.43 Sa se calculeze integralele de suprafat a de primul tip:
1) I =
__
S
(x +y +z) dS, unde o este suprafat a cubului ale carui fet e apart in
planelor de coordonate si planelor x = 1, y = 1, z = 1.
2) I =
__
S
_
x
2
+y
2
_
dS, unde o este sfera x
2
+y
2
+z
2
= a
2
.
3) I =
__
S
_
x
2
+y
2
dS, unde o este suprafat a laterala a conului
x
2
a
2
+
y
2
a
2

z
2
b
2
= 0,
0 z b.
R: 1) Scriem integrala ca suma integralelor pe cele sase fet e ale cubului. I = 9.
2) O reprezentare parametrica a sferei este: x = a cos ucos v, y = a sin ucos v, z =
a sinv, cu (u, v) = [0, 2]
_
2
,

2
, iar |r
u
r
v
| = a
2
cos v. Deci:
I = a
4
_ _
cos
3
ududv =
8
3
a
4
.
3) O reprezentare parametrica a conului este: x = av cos u, y = av sin u, z = bv, cu
(u, v) = [0, 2] [0, 1], iar |r
u
r
v
| = av
a
2
+b
2
. Deci:
I = a
2
_
a
2
+b
2
_ _
v
2
dudv =
2
3
a
2
_
a
2
+b
2
.
12.44 Sa se calculeze integralele de suprafat a de primul tip:
1) I =
__
S
_
y
2
z
2
+z
2
x
2
+x
2
y
2
_
dS, unde o este port iunea din conul z =
_
x
2
+y
2
,
situata n interiorul cilindrului x
2
+y
2
2x = 0.
2) I =
__
S
z dS
x
2
+y
2
+a
2
, unde o este port iunea din paraboloidul 2az = x
2
+y
2
, situata
ntre planele z = 0 si z = h (a > 0, h > 0).
3) I =
__
S
dS
x
2
+y
2
+4z
2
, unde: o =
_
(x, y, z) , x
2
+y
2
+z
2
= a
2
, z 0
_
.
4) I =
__
S
z dS, unde: o = (x, y, z) , x = ucos v, y = usin v, z = v, (u, v) , cu
= [0, a] [0, 2].
5) I =
__
S
_
x
2
+y
2
_
dS, unde o este suprafat a conica z
2
= x
2
+ y
2
, cuprinsa ntre
planele z = 0 si z = 1.
R: 1) I =
29
8

2. 2) I = h
2
. 3) I =
2
3
a
3 ln
_
2 +
3
_
.
4) I =
2
_
a
a
2
+ 1 + ln
_
a +
a
2
+ 1
_
. 5) I =
1
2
2.
12.45 Sa se determine masa suprafet ei omogene ( =
0
): (o) z =
1
h
_
x
2
+y
2
_
, 0
z h, h > 0.
R: /=
0
__
S
dS =
0
__
D
_
1 +
4
h
2
(x
2
+y
2
) dxdy =
1
6
0
h
2
_
5
5 1
_
, unde D =
_
(x, y) , x
2
+y
2
h
2
_
.
12.46 Sa se determine masa suprafet ei (o) z =
1
2
_
x
2
+y
2
_
, 0 z 1, avand densi-
tatea superciala (x, y, z) = z.
R: / =
__
S
zdS =
1
2
__
D
_
x
2
+y
2
_ _
1 +x
2
+y
2
dxdy =
2
15
_
6
3 + 1
_
, unde D =
_
(x, y) , x
2
+y
2
2
_
.
12.47 Sa se determine masa suprafet ei cubului 0 x 1, 0 y 1, 0 z 1, avand
densitatea superciala (x, y, z) = xyz.
R: /=
3
4
.
12.48 Sa se gaseasca coordonatele centrului de greutate al suprafet ei omogene z = x
2
+
y
2
, situata n interiorul cilindrului x
2
+y
2
x = 0.
R: G
_
0, 0,
16
19
_
.
12.49 Sa se determine masa si coordonatele centrului de greutate ale suprafet ei omogene
( = 1): (o) z =
_
1 x
2
y
2
, x 0, y 0, x +y 1.
R: /=
1
2
_
2 1
_
si G
_
1
4
2,
1
4
2,
1
_
2 + 1
__
.
12.50 Sa se calculeze momentul de inert ie n raport cu axa Oz al suprafet ei omogene
( =
0
): (o) x
2
+y
2
+z
2
= a
2
, z 0.
R: I
z
=
4
3
a
4
0
.
12.51 Sa se calculeze momentul de inert ie n raport cu axa Oz al suprafet ei omogene
( =
0
): (o) z =
_
x
2
+y
2
, 0 z h, h > 0.
R: I
z
=
1
2
h
4
2.
12.4 Integrale de suprafat a de tipul al doilea
12.52 Sa se calculeze integralele de suprafat a de tipul al doilea:
1) I =
__
S
yz dydz + zxdzdx + xy dxdy, unde o este fat a exterioara a tetraedrului
marginit de planele de coordonate si de planul x +y +z = a (a > 0).
2) I =
__
S
z dxdy, unde o este fat a exterioara a elipsoidului
x
2
a
2
+
y
2
b
2
+
z
2
c
2
= 1.
3) I =
__
S
x
2
dydz + y
2
dzdx + z
2
dxdy, unde o este fat a exterioara a emisferei x
2
+
y
2
+z
2
= a
2
, z 0.
R: 1) Scriem integrala ca suma integralelor pe cele patru fet e ale tetraedrului:
(o
z
) z = 0, D
z
= (x, y) , x 0, y 0, x +y a ,
(o
x
) x = 0, D
x
= (y, z) , y 0, z 0, y +z a ,
(o
y
) y = 0, D
y
= (z, x) , z 0, x 0, z +x a ,
n care perechile o
z
si D
z
, o
x
si D
x
, o
y
si D
y
au orientari diferite, iar o
0
, fat a cont inuta
n planul x +y +z = a, a carei proiect ii pe planele de coordonate consta n D
z
, D
x
, D
y
,
avand aceeasi orientare cu o
0
. Astfel
_ _
S
xy dxdy =
_ _
S
z
xy dxdy +
_ _
S
0
xy dxdy =
_ _
D
xy dxdy +
_ _
D
xy dxdy = 0.
Rezultate identice avem pentru ceilalt i doi termeni. Deci I = 0.
2) Integrala sa reduce la
I =
_ _
D
_
1
x
2
a
2

y
2
b
2
dxdy,
unde D
z
=
_
(x, y) ,
x
2
a
2
+
y
2
b
2
1
_
. Se obt ine I =
4
3
abc. 3) I =
1
2
a
4
.
12.53 Sa se calculeze integralele de suprafat a de tipul al doilea:
1) I =
__
S
y dydz+z dzdx+3xdxdy, unde o este fat a interioara a sferei x
2
+y
2
+z
2
=
a
2
, situata n primul octant.
2) I =
__
S
x
2
y
2
z dxdy, unde o este fat a exterioara a emisferei x
2
+ y
2
+ z
2
= R
2
,
z 0.
3) I =
__
S
xz dydz+yz dzdx+
_
x
2
+y
2
_
dxdy, unde o este fat a superioara a suprafet ei
(o) z = x
2
+y
2
, care se proiecteaza ortogonal pe planul Oxy n domeniul
D =
_
(x, y) , x
2
+y
2
1
_
.
4) I =
__
S
dxdy
4x
2
+y
2
+1
, unde o este fat a exterioara a paraboloidului (o) z = 4x
2
+y
2
,
0 z 1.
5) I =
__
S
x
2
dydz + y
2
dzdx + z
2
dxdy, unde o este fat a exterioara a tetraedrului cu
varfurile n punctele O(0, 0, 0), A(1, 0, 0), B(0, 1, 0), C (0, 0, 1).
6) I =
__
S
_
x
2
+y
2
_
z dxdy, unde o este fat a exterioara a paraboloidului (o) z =
x
2
+y
2
, situata n interiorul cilindrului x
2
+y
2
= 1.
7) I =
__
S
dydz
x
+
dzdx
y
+
dxdy
z
, unde o este fat a exterioara a elipsoidului (o)
x
2
a
2
+
y
2
b
2
+
z
2
c
2
= 1.
R: 1) Deoarece cos =
x
a
, cos =
y
a
, cos =
z
a
, avem
I =
1
a
_ _
S
(xy +yz + 3zx) dS,
cu (o) x = a cos usin v, y = a sin usin v, z = a cos v, (u, v)
_
0,

2
_
0,

2
. Deoarece
dS = a
2
sin v dudv, se obt ine I = 2a
3
. 2) I =
2
105
R
7
. 3) Versorul normalei la suprafat a
n punctul M (x, y, z) este n =
1
1+4x
2
+4y
2
(2xi 2yj +k), a..
I =
_ _
S
_
x
2
+y
2
_
(1 2z)
_
1 + 4x
2
+ 4y
2
dS =
6
.
4) Deoarece cos =
1
1+64x
2
+4y
2
, urmeaza ca I =
__
D
dxdy
4x
2
+y
2
+1
=
_
1
2
_
,
unde D =
_
(x, y) , 4x
2
+y
2
1
_
. 5) I =
1
12
. 6) I =
25
84
. 7) O reprezentare parametrica
a elipsoidului este (o) x = a cos usin v, y = b sin usin v, z = c cos v, (u, v) , cu
= [0, 2] [0, ]. Rezulta
I =
_
bc
a
+
ca
b
+
ab
c
__ _
sin v dudv =
4
abc
_
b
2
c
2
+c
2
a
2
+a
2
b
2
_
.
12.54 Utilizand formula lui Stokes, sa se calculeze urmatoarele integrale curbilinii, pe
curbele nchise (, parcurse n sens direct:
1) I =
_
C
(x + 3y + 2z) dx+(2x +z) dy+(x y) dz, unde ( este conturul triunghiului
cu varfurile n punctele A(2, 0, 0), B(0, 3, 0), C (0, 0, 1).
2) I =
_
C
x
2
y
3
dx +dy +z dz, unde (() x
2
+y
2
= r
2
, z = 0.
3) I =
_
C
(y +z) dx+(z +x) dy+(x +y) dz, unde (() x
2
+y
2
+z
2
= a
2
, x+y+z = 0.
4) I =
_
C
_
y
2
+z
2
_
dx +
_
z
2
+x
2
_
dy +
_
x
2
+y
2
_
dz, unde (() x
2
+ y
2
+ z
2
= 4x
2
,
x
2
+y
2
= 2x, z 0.
5) I =
_
C
(z y) dx + (x z) dy + (y x) dz, unde ( este conturul triunghiului cu
varfurile n punctele A(a, 0, 0), B(0, b, 0), C (0, 0, c).
6) I =
_
C
y
2
dx + z
2
dy + x
2
dz, unde (() x
2
+ y
2
+ z
2
= a
2
, x
2
+ y
2
= ax (curba lui
Viviani).
7) I =
_
C
(y z) dx + (z x) dy + (x y) dz, unde (() x
2
+y
2
= 1, x +z = 1.
8) I =
_
C
xdx + (x +y) dy + (x +y +z) dz, unde (() x = a sin t, y = a cos t, z =
a (sin t + cos t), t [0, 2].
9) I =
_
C
dx
1+x
2
+
y dy
x
+xdz, unde (() x
2
+y
2
= 2x, x +y +z = 0.
R: 1) Deoarece F(x, y, z) = (x + 3y + 2z) i+(2x +z) j+(x y) k si rot F = 2i+j
k, o ind suprafat a triunghiului cu varfurile n punctele A(2, 0, 0), B(0, 3, 0), C (0, 0, 1)
din planul
x
2
+
y
3
+
z
1
1 = 0 si deci n =
1
7
(3i + 2j + 6k), rezulta I =
__
S
(nrot F) dS = 5.
2) I =
1
8
r
6
. 3) I = 0. 4) Deoarece cos =
x2
2
, cos =
y
2
, cos =
z
2
, rezulta
I =
__
D
(z y) dS = 4. 5) I = ab +bc +ca. 6) Avem
I = 2
_ _
D
_
x +y +
xy
_
a
2
x
2
y
2
_
dxdy =
4
a
3
,
cu D =
_
(x, y) , x
2
+y
2
ax
_
. 7) I = 4. 8) I = a
2
. 9) I = .
12.5 Integrala tripla
12.55 Sa se calculeze integralele triple:
1) I =
___
V
x
3
y
2
z dxdydz, unde V = (x, y, z) , 0 x 1, 0 y x, 0 z xy.
2) I =
___
V
x
2
dxdydz, unde V =
_
(x, y, z) ,
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1
_
.
3) I =
___
V
z dxdydz, unde V =
_
(x, y, z) ,
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1, z 0
_
.
R: 1) I =
_
1
0
dx
_
x
0
dy
_
xy
0
x
3
y
2
z dz =
1
110
. 2) Domeniul spat ial V este simplu n
raport cu axa Oz, deci
V =
_
(x, y, z) , c
_
1
x
2
a
2

y
2
b
2
z c
_
1
x
2
a
2

y
2
b
2
, (x, y) D,
_
unde D =
_
(x, y) ,
x
2
a
2
+
y
2
b
2
1
_
. Deci
I =
_ _
D
dxdy
_
c
1
x
2
a
2
y
2
b
2
c
1
x
2
a
2
y
2
b
2
x
2
dz = 2c
_ _
D
x
2
_
1
x
2
a
2

y
2
b
2
dxdy.
Domeniul plan D este simplu n raport cu axa Oy, deci
D =
_
(x, y) , b
_
1
x
2
a
2
y b
_
1
x
2
a
2
, x [a, a]
_
,
ncat
I = 2c
_
a
a
dx
_
b
1
x
2
a
2
b
1
x
2
a
2
x
2
_
1
x
2
a
2

y
2
b
2
dy = bc
_
a
a
x
2
_
1
x
2
a
2
_
dx =
4
15
a
3
bc.
3) I =
1
4
abc
2
.
12.56 Sa se calculeze integralele triple:
1) I =
___
V
dxdydz
(1+x+y+z)
3
, unde V este tetraedrul delimitat de planele de coordonate si
planul x +y +x = 1.
2) I =
___
V
xyz
(1+x
2
+y
2
+z
2
)
4
dxdydz, unde V = [0, 1] [0, 1] [0, 1].
3) I =
___
V
dxdydz
(1+x
2
+y
2
z)
3
, unde
V
_
(x, y, z) , x
2
+y
2
z, x
2
+y
2
1, z 0
_
.
4) I =
___
V
z dxdydz, unde
V =
_
(x, y, z) , 0 x
1
2
, x y 2x, 0 z
_
1 x
2
y
2
_
.
5) I =
___
V
x
2
dxdydz, unde V =
_
(x, y, z) , x
2
+y
2
+z
2
R
2
_
.
6) I =
___
V
x
x
2
+y
2
+z
2
+a
2
dxdydz, unde: V = (x, y, z) [ x
2
+ y
2
+ z
2
R
2
, x
0, y 0, z 0.
7) I =
___
V
z
_
x
2
+y
2
dxdydz, unde V este domeniul marginit de cilindrul x
2
+y
2
=
2x si planele y = 0, z = 0, z = a (a < 0).
R: 1) Domeniul V este simplu n raport cu axa Oz:
I =
_ _
D
dxdy
_
1xy
0
dz
(1 +x +y +z)
3
=
1
2
_ _
D
_
1
(1 +x +y)
2

1
4
_
dxdy,
unde D = (x, y) , 0 y 1 x, x [0, 1], deci
I =
1
2
_
1
0
_
1
1 +x

3 x
4
_
dx = ln
2
5
16
.
2) I =
_
1
0
dx
_
1
0
dy
_
1
0
xyz
(1+x
2
+y
2
+z
2
)
4
dz =
1
192
. 3) Domeniul V este simplu n raport cu
axa Oz:
I =
_ _
D
dxdy
_
x
2
+y
2
0
dz
(1 +x
2
+y
2
z)
3
2
= 2
_ _
D
_
1
_
1 +x
2
+y
2
_
1
2
_
dxdy,
unde D =
_
(x, y) , x
2
+y
2
1
_
. Trecand la coordonate polare, avem I = 2
_
2
2 3
_
.
4) I =
_ 1
2
0
dx
_
2x
x
_
1x
2
y
2
0
z dz =
1
2
_ 1
2
0
_
x
10
3
x
3
_
dx =
7
192
. 5) Trecem la coordo-
nate sferice:
_
_
_
x = r cos sin,
y = r sin sin ,
z = r cos ,
(r, , ) [0, R] [0, 2] [0, ] .
Deoarece J(r, , ) = r
2
sin , avem
I =
_
_
R
0
r
4
dr
_
__
2
0
cos
2
d
___

0
sin
3
d
_
=
4
15
R
5
.
6) Trecem la coordonate sferice:
_
_
_
x = r cos sin ,
y = r sin sin ,
z = r cos ,
(r, , ) [0, R]
_
0,

2
_
_
0,

2
_
.
Deoarece dxdydz = r
2
sin drdd, avem
I =
_
2
0
d
_
2
0
d
_
R
0
r
3
sin
2
cos
r
2
+a
2
dr =

8
_
R
2
+a
2
ln
a
2
a
2
+R
2
_
.
7) Trecem la coordonate cilindrice: x = r cos , y = r sin , z = z, (r, , z) V
, unde
V
=
_
(r, , z) , 0 r 2 cos , 0

2
, 0 z a
_
. Deoarece J (r, , z) = r, avem
I =
_ _ _
V
zr
2
drddz =
_ _
D
drd
_
a
0
zr
2
dz =
a
2
2
_ _
D
r
2
drd,
unde D
=
_
(r, ) , 0 r 2 cos , 0

2
_
, deci
I =
a
2
2
_
2
0
d
_
2 cos
0
r
2
dr =
4a
2
3
_
2
0
cos
3
d =
8a
2
9
.
12.57 Sa se calculeze urmatoarele integrale triple:
1) I =
___
V
xyz dxdydz, unde V este domeniul spat ial marginit de sfera x
2
+y
2
+z
2
=
1, situat n primul octant.
2) I =
___
V
xy
2
z
3
dxdydz, unde V este domeniul spat ial marginit de suprafet ele z =
xy, y = x, x = 1, z = 0.
3) I =
___
V
(2x + 3y z) dxdydz, unde V este prisma triunghiulara marginit a de
planele x = 0, y = 0, z = 0, z = a, x +y = b, cu a, b > 0.
4) I =
___
V
_
x
2
+y
2
+z
2
_
3
dxdydz, unde V este domeniul spat ial marginit de cilin-
drul x
2
+y
2
= 1 si planele y = 0, y = 1.
5) I =
___
V
_
1 + (x
2
+y
2
+z
2
)
3
2
dxdydz, unde V =
_
(x, y, z) , x
2
+y
2
+z
2
1
_
.
6) I =
___
V
_
x
2
+y
2
_
dxdydz, unde V este domeniul spat ial marginit de suprafet ele
2z = x
2
+y
2
, z = 2.
7) I =
___
V
_
x
2
+y
2
_
z dxdydz, unde V este domeniul spat ial marginit de paraboloi-
dul z = x
2
+y
2
si sfera x
2
+y
2
+z
2
= 6.
8) I =
___
V
z dxdydz, unde V este domeniul spat ial marginit de conul
z =
a
R
_
x
2
+y
2
si planul z = a, cu a, R > 0.
R: 1) I =
1
48
. 2) I =
1
364
. 3) I =
1
12
ab
2
(10b 3a). 4) I =
3
2
. 5) I =
8
9
_
2
2 1
_
.
6) I =
16
3
. 7) I =
8
3
. 8) I =
1
4
a
2
R
2
.
12.58 Sa se calculeze urmatoarele integrale triple:
1) I =
___
V
dxdydz
x
2
+y
2
+z
2
, unde V este domeniul spat ial marginit de sferele x
2
+y
2
+z
2
=
1, x
2
+y
2
+z
2
= 4, z 0.
2) I =
___
V
_
x
2
a
2
+
y
2
b
2
+
z
2
c
2
_
dxdydz, unde V =
_
(x, y, z) ,
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1
_
.
3) I =
___
V
_
x
2
+y
2
+z
2
_
dxdydz, unde
V =
_
(x, y, z) , x
2
+y
2
z
2
, x
2
+y
2
+z
2
a
2
, z > 0
_
.
4) I =
___
V
_
x
2
+y
2
+z
2
_
dxdydz, unde
V =
_
(x, y, z) , x
2
+y
2
+z
2
2az, x
2
+y
2
+z
2
3a
2
_
, cu a > 0.
5) I =
___
V
_
x
2
+y
2
+z
2
dxdydz, unde V =
_
(x, y, z) , x
2
+y
2
+z
2
x
_
.
6) I =
___
V
x
2
dxdydz, unde V este domeniul spat ial marginit de suprafet ele z = ay
2
,
z = by
2
cu y > 0 si 0 < a < b si de suprafet ele z = x, z = x, 0 < < si z = h,
h > 0.
7) I =
___
V
x dxdydz
(x
2
+y+z+1)
3
, unde
V = (x, y, z) , x +y +z 1, x 0, y 0, z 0.
8) I =
___
V
z
3
dxdydz
(y+z)(x+y+z)
, unde
V = (x, y, z) , x +y +z 1, x 0, y 0, z 0.
9) I =
___
V
_
1
_
x
2
a
2
+
y
2
b
2
+
z
2
c
2
_
dxdydz, unde
V =
_
(x, y, z) ,
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1
_
.
10) I =
___
V
z dxdydz, unde V =
_
(x, y, z) , x
2
+y
2
+z
2
8, x
2
+y
2
z
2
, z 0
_
.
11) I =
___
V
_
x
2
+y
2
+z
2
dxdydz, unde V =
_
(x, y, z) , x
2
+y
2
+z
2
z
_
.
12) I =
___
V
dxdydz
x
2
+y
2
+z
2
, unde
V =
_
(x, y, z) , x
2
+y
2
+z
2
4, x
2
+y
2
+z
2
16
_
.
13) I =
___
V
_
x
2
+y
2
+z
2
_
dxdydz, unde V este domeniul spat ial marginit de sfera
x
2
+y
2
+z
2
= 9 si conul z =
_
x
2
+y
2
.
R: 1) Se trece la coordonate sferice. Avem V
= [1, 2] [0, 2]
_
0,

2
, I = 2. 2)
Se trece la coordonate sferice generalizate:
_
_
_
x = ar cos sin ,
y = br sinsin ,
z = cr cos ,
(r, , ) [0, 1] [0, 2] [0, ] .
Deoarece J(r, , ) = abcr
2
sin , rezulta I =
4
5
abc. 3) I =
1
5
a
5
_
2
2
_
. 4) I =
1
5
a
5
_
18
3
97
6
_
. 5) I =
1
10
. 6) I =
2
27
_
1
3

1
3
__
1
a

1
b
_
h
4
h. 7) I =
1
4
ln
2+
1
7
arctg
1
7
+
1
2
3
_
arctg
3 arctg
1
3
_
. 8) I =
1
64
. 9) I =
1
4
2
abc. 10) I = 8. 11)
I =
1
10
. 12) I = 24. 13) I =
243
5

_
2
2
_
.
12.59 Sa se calculeze, cu ajutorul integralei triple, volumul domeniului spat ial
V =
_
(x, y, z) , x 0, y 0, z 0, z 1 y
2
, x +y 1
_
.
R: 1 =
___
V
dxdydz =
_
1
0
dx
_
1x
0
dy
_
1y
2
0
dz =
5
12
.
12.60 Sa se calculeze, cu ajutorul integralei triple, volumul domeniului spat ial marginit
de suprafet ele
1) y
2
= 4a
2
3ax, y
2
= ax, z = h.
2) x
2
+y
2
+z
2
= a
2
, x
2
+y
2
= ax.
3) y = x
2
, y = 1, x +y +z = 3, z = 0.
R: 1) 1 =
32
9
a
2
h. 2) 1 =
1
9
(3 4) a
3
. 3) 1 =
_
1
1
dx
_
1
x
2
dy
_
3xy
0
dz =
16
5
.
12.61 Utilizand formula lui Gauss-Ostrogradski, sa se calculeze urmatoarele integrale
de suprafat a pe suprafet ele nchise o ce marginesc domeniile spat iale V , n ind versorul
normalei la fat a exterioara:
1) I =
__
S
x
3
y
2
dydz +x
2
y
3
dzdx + 3z dxdy, unde o este frontiera domeniului spat ial
V marginit de paraboloizii z = x
2
+y
2
, z = 6 x
2
y
2
, 0 z 6.
2) I =
__
S
x
2
dydz + y
2
dzdx + z
2
dxdy, unde o este frontiera domeniului spat ial
V = [0, a] [0, a] [0, a], a > 0.
3) I =
__
S
x
3
dydz +y
3
dzdx +z
3
dxdy, unde o este sfera x
2
+y
2
+z
2
= a
2
.
4) I =
__
S
2x
2
yz dydz +z
2
dzdx+xyz
2
V =
_
(x, y, z) ,
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1, z 0
_
.
5) I =
__
S
xdydz + y dzdx + z dxdy, unde o este frontiera piramidei delimitata de
planele x = 0, y = 0, z = 0, x +y +z = a.
6) I =
__
S
_
x
2
cos +y
2
cos +z
2
cos
_
dS, unde o este frontiera domeniului spat ial
V =
_
(x, y, z) ,
x
2
a
2
+
y
2
a
2

z
2
b
2
, 0 z b
_
.
7) I =
__
S
yz dydz + zxdzdx + xy dxdy, unde o este frontiera unui domeniu spat ial
V .
8) I =
__
S
xyz (xdydz +y dzdx +z dxdy), unde o este frontiera domeniului spat ial
V =
_
(x, y, z) , x
2
+y
2
+z
2
a
2
, x 0, y 0, z 0
_
.
9) I =
__
S
x
3
dydz + x
2
y dzdx + x
2
z dxdy, unde o este frontiera domeniului spat ial
V =
_
(x, y, z) , x
2
+y
2
R
2
, 0 z a
_
, a > 0.
10) I =
__
S
x
2
dydz + y
2
dzdx + z
2
dxdy, unde o este sfera (x a)
2
+ (y b)
2
+
(z c)
2
= R
2
.
11) I =
__
S
xdydz+y dzdx+
_
x
2
+y
2
V =
_
(x, y, z) , x
2
+y
2
+z
1
4
,
_
x
2
+y
2
z 2
_
x
2
+y
2
_
.
12) I =
__
S
y
2
z dydz + xz dzdx + x
2
V marginit de paraboloidul z = x
2
+y
2
, cilindrul x
2
+y
2
= 1, situat n primul octant.
13) I =
__
S
x
2
dydz +y
2
dzdx +z
2
dxdy, nde o este frontiera tetraedrului cu varfurile
n punctele O(0, 0, 0), A(1, 0, 0), B(0, 1, 0), C (0, 0, 1).
R: 1) Deoarece F(x, y, z) = x
3
y i +x
2
y
3
j +3z k si div F = 3
_
2x
2
y
2
+ 1
_
, putem scrie
I =
_ _ _
V
(div F) d = 3
_ _ _
V
_
2x
2
y
2
+ 1
_
dxdydz =
=
_ _
D
dxdy
_
6x
2
y
2
x
2
+y
2
_
2x
2
y
2
+ 1
_
dz,
unde D =
_
(x, y) , x
2
+y
2
3
_
. Se obt ine I =
297
8
. 2) I = 3a
4
. 3) I =
12
5
a
5
. 4)
I =
3
2
abc
2
. 5) I =
1
2
a
3
. 6) I =
1
2
a
2
b
2
. 7) I = 0. 8) I =
1
8
a
6
. 9) I =
5
4
aR
4
. 10)
I =
8
3
R
3
(a +b +c). 11) I =
1
96
_
8
3+2
2

20
9+4
5
_
. 12) I =
1
8
. 13) I =
1
12
.
12.62 Sa se calculeze masa cubului de densitate (x, y, z) = x + y + z, care ocup a
domeniul spat ial V = [0, a] [0, a] [0, a], a > 0.
R: /=
3
2
a
4
.
12.63 Sa se calculeze masa corpului de densitate (x, y, z) = x, care ocupa domeniul
spat ial V marginit de suprafet ele x
2
= 2y, y +z = 1, 2y +z = 2.
R: /=
8
35
2.
12.64 Sa se calculeze coordonatele centrului de greutate ale corpului omogen care ocupa
domeniul spat ial
V =
_
(x, y, z) ,
x
2
a
2
+
y
2
b
2
+
z
2
c
2
1, x 0, y 0, z 0
_
.
R: G
_
3a
8
,
3b
8
,
3c
8
_
.
domeniul spat ial marginit de suprafet ele x
2
+y
2
= z, x +y +z = 0.
R: G
_
1
2
,
1
2
,
5
6
_
.
domeniul spat ial
V =
_
(x, y, z) , x
2
+y
2
2z, x +y z
_
.
R: G
_
1, 1,
5
3
_
.
domeniul spat ial
V =
_
(x, y, z) , x
2
+y
2
a
2
, z by, z 0
_
, b > 0.
R: G
_
0,
3
16
a,
3
32
ab
_
.
12.68 Sa se calculeze momentul de inert ie n raport cu axa Oz al corpului omogen
( = 1), care ocupa domeniul spat ial marginit de suprafet ele x
2
+y
2
+z
2
= 2, x
2
+y
2
= z
2
,
z 0.
R: I
z
=
4
15
_
4
2 5
_
.
12.69 Sa se calculeze momentul de inert ie n raport cu axele de coordonate si n raport
cu originea ale piramidei omogene ( = 1), marginita de planele de coordonate si de
planul x +y +z = 1.
R: I
x
= I
y
= I
z
=
1
30
, I
0
=
1
20
.
12.70 Sa se calculeze momentele de inert ie n raport cu planele de coordonate ale cor-
pului omogen ( = 1), care ocupa domeniul spat ial marginit de suprafet ele
x
2
a
2
+
y
2
b
2
=
z
2
c
2
,
z = c, c > 0.
R: I
yz
=
1
5
a
3
bc, I
zx
=
1
5
ab
3
c, I
xy
=
1
5
abc
3
.
12.71 Sa se calculeze momentul de inert ie n raport cu axa Oz al corpului omogen
( = 1), care ocupa domeniul spat ial
V =
_
(x, y, z) ,
x
2
a
2
+
y
2
b
2

z
2
c
2
, 0 z h
_
, h > 0.
R: I
z
=
1
5
ab
c
2
h
5
.
12.72 Sa se calculeze momentul de inert ie n raport cu planul Oxy al corpului avand
densitatea (x, y, z) =
z
(x
2
+y
2
+2z
2
+a
2
)
2
, care ocupa domeniul spat ial
V =
_
(x, y, z) , x
2
+y
2
z
2
, 0 z a
_
, a > 0.
R: I
xy
=
1
12
a
2
ln
_
16
3
27
a
4
_
.
12.73 Sa se calculeze momentul de inert ie n raport cu originea al corpului omogen
marginit de sfera de raza 2 cu centrul n origine.
R: I
0
=
128
5
.
Capitolul 13
Ecuat ii diferent iale ordinare
13.1 Ecuat ii diferent iale de ordinul ntai
13.1 Sa se integreze ecuat ia (t
2
x
2
) dt 2txdx = 0 si apoi sa se determine curba
integrala care trece prin punctul (1, 1).
R: Avem P(t, x) = t
2
x
2
, Q(t, x) = 2tx si P
x
= Q
t
= 2x, deci membrul stang al
ecuat iei date este o diferent iala exacta. Atunci integrala generala este data de
_
t
t
0
(
2
x
2
0
) d 2
_
x
x
0
t d = C, (t
0
, x
0
) D.
sau
1
3
t
3
tx
2
= C. Solut ia particulara care satisface condit ia init iala data este t
3
3tx
2
+
2 = 0.
13.2 Sa se gaseasca integrala particular a a ecuat iei
_
t +e
t
x
_
dt + e
t
x
_
1
t
x
_
dx = 0,
care verica condit ia init ial a x(0) = 2.
R:
1
2
t
2
+xe
t
x
= 2.
13.3 Sa se integreze urmatoarele ecuat ii diferent iale care provin din anularea unei di-
ferent iale exacte:
1)
_
3t
2
+ 6tx
2
_
dt +
_
6t
2
x + 4x
3
_
dx = 0.
2) (t +x) dt + (t + 2x) dx = 0.
3)
_
t
2
+ 2t +x
2
_
dt + 2txdx = 0.
4)
_
t
3
3tx
2
+ 2
_
dt
_
3t
2
x x
2
_
dx = 0.
5) (e
t
+x + sin x) dt + (e
x
+t +t cos x) dx = 0.
6) (t +x 1) dt + (e
x
+t) dx = 0.
7)
_
x
t
2
+x
2
x
_
dt +
_
e
x
t
t
t
2
+x
2
_
dx = 0.
8)
_
tg x
x
sin
2
t
_
dt +
_
ctg t +
t
cos
2
x
_
dx = 0.
R: 1) t
3
+ 3t
2
x
2
+x
4
= C. 2)
1
2
t
2
+tx +x
2
= C. 3)
1
3
t
3
+t
2
+tx
2
= C.
4)
1
4
t
4
3
2
t
2
x
2
+2t +
1
3
x
3
= C. 5) e
t
+tx+t sin x+e
x
= C. 6) e
x
+
1
2
t
2
+txt = C.
7) arctg
t
x
tx +e
x
= C. 8) t tg x +xctg t = C.
168
CAPITOLUL 13. ECUAT II DIFERENT IALE ORDINARE 169
13.4 Sa se integreze urmatoarele ecuat ii diferent iale care provin din anularea unei di-
ferent iale exacte:
1)
_
e
t+x
+ 3t
2
_
dt +
_
e
t+x
+ 4x
3
_
dx = 0, cu x(0) = 0.
2) (arcsin t + 2tx) dt +
_
t
2
+ 1 + arctg x
_
dx = 0.
3)
_
ln x 5x
2
sin 5t
_
dt +
_
t
x
+ 2xcos 5t
_
dx = 0, cu x(0) = e.
4) [sin x + (1 x) cos t] dt + [(1 +t) cos x sin t] dx = 0.
5)
_
2txe
t
2
+ ln x
_
dt +
_
e
t
2
+
t
x
_
dx = 0, cu x(0) = 1.
6) (t +x + 1) dt +
_
t x
2
+ 3
_
dx = 0.
7) (sin tx = txcos tx) dt +t
2
cos txdx = 0.
8)
_
t
3
+tx
2
_
dt +
_
t
2
x +x
3
_
dx = 0.
R: 1) e
t+x
+t
3
+x
4
= 1. 2) t arcsin t +
1 t
2
+t
2
x+xarctg xln
1 +x
2
+x = C.
3) t ln x +x
2
cos 5t = e
2
. 4) (1 +t) sin x + (1 x) sin t = C. 5) xe
t
2
+t ln x = 1.
6)
1
2
t
2
+t +tx
1
3
x
3
= 3x = C. 7) t sin tx = C. 8) t
4
+ 2t
2
x
2
+x
4
= C.
13.5 Sa se determine solut ia ecuat iei (x
2
+ 1)dt + (2t + 1)x
2
dx = 0, care trece prin
punctul (1, 0).
R: Separand variabilele, avem
1
2t+1
dt +
x
2
x
2
+1
dx = 0, cu solut ia generala
1
2
ln (2t + 1) +x arctg x = C.
Solut ia particulara care sasface condit ia data este
1
2
ln (2t + 1) +x arctg x =
1
2
ln 3.
13.6 Sa se integreze urmatoarele ecuat ii diferent iale cu variabile separabile:
1) xdt +t dx = 0. 2) tx
x = x
3
.
3) txx
= 1 t
2
. 4) tg t sin
2
xdt + ctg xcos
2
t dx = 0.
5) dx =
_
t
2
+ 1
_ _
x
2
+ 1
_
dt. 6)
_
t
2
1
_
x
tx = 0.
7) x
+ sin (t +x) = sin (t x) . 8) x
= sh (t +x) + sh (t x) .
R: 1) Ecuat ia se mai scrie, separand variabilele:
1
t
dt +
1
x
dx = 0. De unde ln[t[ +
ln [x[ = ln [C[, sau tx = C.
2) t
2
_
1 +x
2
_
= Cx
2
. 3) x
2
2 ln t +t
2
= C. 4) ctg
2
x = tg
2
t +C.
5) x = tg
_
1
3
t
3
+t +C
_
. 6) x
2
= C
_
t
2
1
_
. 7) ln
tg
x
2
+ 2 sin t = C.
8) x = ln [tg (cht +C)].
13.7 Sa se integreze urmatoarele ecuat ii diferent iale cu variabile separabile, cu condit iile
init iale precizate:
1) (1 +e
t
) xx
= e
t
, cu x(0) = 1.
2)
_
1 +e
2t
_
x
2
dx = e
t
dt, cu x(0) = 0.
3) x
+ cos (t + 2x) = cos (t 2x) , cu x(0) =

4
.
4) e
1+t
2
th xdt
1
t1
e
2t
dx = 0, cu x(1) =

2
.
5) x
= e
t+x
+e
tx
, cu x(0) = 0.
6) x(t + 2) dt +t (x 1) dx = 0, cu x(1) = 1.
7) t
_
x
6
+ 1
_
dt +x
2
_
t
4
+ 1
_
dx = 0, cu x(0) = 1.
R: 1) x
2
= 1 + 2 ln
1+e
t
2
. 2)
1
3
x
3
+

4
= arctg e
t
. 3) ln [tg x[ = 4 (1 cos t).
4) ln sin
2
x = e
(x1)
2
1. 5) x = ln
_
e
t
+

4
1
_
. 6) t +x + 2 ln t ln x = 2.
7) 3arctg t
2
+ 2arctg x
3
=

2
.
13.8 Sa se integreze urmatoarele ecuat ii diferent iale cu variabile separabile:
1) (cos t sin t + 1) x
= cos x sin x 1. 2) 2t
1 x
2
= x
_
1 +t
2
_
.
3) e
t
sin
3
x +
_
1 +e
2t
_
(cos x) x
= 0. 4) x
2
(sin t) +
_
cos
2
t
_
(ln x) x
= 0.
5) x
= sin (t x) . 6) x +tx
= a (1 +tx) .
7) (tx 1)
2
tx
+
_
t
2
x
2
+ 1
_
x = 0. 8) t
1 +x
2
+x
1 +t
2
x
= 0.
R: 1) tg
x
2
= C
_
1 + tg
x
2
_ _
1 tg
t
2
_
. 2) x = sin
_
C ln
_
1 +t
2
_
.
3) arctg e
t
=
1
2 sin
2
x
+C. 4) x = (1 + ln x +Cx) cos t. 5) t +C = ctg
_
xt
2
+

4
_
.
6) 1 +tx = Ce
at
. 7) Cu schimbarea de funct ie u = tx, obt inem x
2
= Ce
tx
1
tx
.
8)

1 +t
2
+
1 +x
2
= C.
13.9 Sa se determine un factor integrant si sa se integreze ecuat ia
(t
3
sin x 2x)dt + (t
4
cos x +t)dx = 0.
R: Avem P
x
= t
3
cos x 2, Q
t
= 4t
3
cos x + 1 si deci
1
Q
_
P
x

Q
t
_
=
3
t
este funct ie numai de t. Ca atare avem
1
d
dt
=
3
t
si o solut ie particulara este =
1
t
3
.
Inmult ind ecuat ia cu , obt inem

_
sinx
2x
t
3
_
dt +
_
t cos x +
1
t
2
_
dx = 0
a carei solut ie generala este t sin x +
x
t
2
= C.
13.10 Sa se integreze urmatoarele ecuat ii diferent iale stiind ca admit un factor integrant
de forma = (t):
1)
_
2tx +t
2
x +
1
3
x
3
_
dt +
_
t
2
+x
2
_
dx = 0.
2)
_
t +x
2
_
dt 2txdx = 0.
3) (t sin x +xcos x) dt + (t cos x xcos x) dx = 0.
4) (t + sin t + sin x) dt + cos xdx = 0.
R: 1) = e
t
, xe
t
_
t
2
+
1
3
x
2
_
= C. 2) =
1
t
2
, ln [t[
1
t
x
2
= C.
3) = e
t
, (t sinx +xcos x sin x) e
t
= C.
4) = e
t
, 2e
t
sin x + 2e
t
(t 1) +e
t
(sin t cos t) = C.
de forma = (x):
1) x(1 +tx) dt t dx = 0. 2) xdt
_
t +x
2
_
dx = 0.
3) 2tx(ln x) dt +
_
t
2
+x
2
1 +x
2
_
dx = 0. 4)
_
1 + 3t
2
sinx
_
dt tctg xdx = 0.
R: 1) =
1
x
2
,
t
x
+
1
2
t
2
= C. 2) t = x(x +C).
3) =
1
x
, t
2
ln [x[ +
1
3
_
x
2
+ 1
_3
2
= C. 4) =
1
sin x
,
t
sin x
+t
3
= C.
de forma indicata:
1) (t x) dt + (t +x) dx = 0, =
_
t
2
+x
2
_
.
2) tx
2
dt +
_
t
2
x t
_
dx = 0, = (tx)
3)
_
2t
3
+ 3t
2
x +x
2
x
3
_
dt +
_
2x
3
+ 3tx
2
+t
2
t
3
_
dx = 0, = (t +x) .
4)
_
t
2
+x
2
+ 1
_
dt 2txdx = 0, =
_
x
2
t
2
_
.
5) (t tx) dt +
_
t
2
+x
_
dx = 0, =
_
t
2
+x
2
_
.
6)
_
3t + 2x +x
2
_
dt +
_
t + 4tx + 5x
2
_
dx = 0,
_
t +x
2
_
.
R: 1) =
1
t
2
+x
2
,
1
2
ln
_
t
2
+x
2
_
arctg
t
x
= C. 2) tx ln [x[ = C.
3) t
3
+tx +x
3
= C (t +x). 4) =
_
x
2
t
2
+ 1
_
2
, x
2
t
2
+ 1 = Cx.
5) =
_
t
2
+x
2
_3
2
, x 1 = C
t
2
+x
2
. 6) = t +x
2
, (t +x)
_
t +x
2
_
2
= C.
13.13 Sa se gaseasca solut ia ecuat iei omogene t
2
+ 2x
2
= txx
, care satisface condit ia

init iala x(1) = 2.
R:Cu schimbarea de variabila x = ty, ecuat ia devine
ydy
1+y
2
=
dt
t
, cu solut ia generala
t = C
_
1 +y
2
.

Inlocuind pe y, avem t
2
= C
t
2
+x
2
. Condit ia init iala determina pe
C =
1
5
. Solut ia particulara cautata este t
2
5 =
t
2
+x
2
.
13.14 Sa se integreze urmatoarele ecuat ii diferent iale omogene:
1) tx
= x t. 2) tx
= x +te
x
t
. 3) tx
= t x.
4) t
2
x
= x(t x) . 5) tx
= x +ttg
x
t
. 6) (t x) x
= t +x.
7) tx
= x +t cos
2 x
t
. 8) 2t
2
x
= t
2
+x
2
. 9) txx
+ 2tx +t
2
= 0.
R: 1) Prin schimbarea de funct ie x = ty ecuat ia se transforma ntr-o ecuat ie cu
variabile separabile: y
=
1
t
, de unde x = t ln
C
t
.
2) Se obt ine ty
= e
y
, de unde x = t ln ln
C
t
.
3) Se obt ine ty
= 1 2y, de unde x =
C
t

t
2
. 4) t = Ce
t
x
.
5) sin
x
t
= Ct. 7) tg
x
t
= ln (Ct). 8) 2t = (t x) ln (Ct). 9) ln [t +x[ +
t
t+x
= C.
13.15 Sa se integreze urmatoarele ecuat ii diferent iale omogene, cu condit iile init iale
precizate:
1) tx
sin
x
t
+t = xsin
x
t
, cu x(1) = 0.
2) t
2
x
= x
2
+tx +t
2
, cu x(1) = 2.
3) 4tx
_
t
2
+x
2
_
x
+x
4
+ 6t
2
x
2
+t
4
, cu x(1) = 0.
4)
_
x 3t sin
3t
x
_
x
+ 3xsin
3t
x
= 0, cu x
_
3
_
= 1.
R: Avem:
1) te = e
cos
x
t
. 2) arctg
x
2t
2 ln [t[ =

4
. 3) t
5
+10t
3
x
2
+5tx
4
= 1. 4) ln [x[cos
3t
x
= 1.
13.16 Sa se integreze urmatoarele ecuat ii diferent iale reductibile la ecuat ii omogene:
1) (t +x 3) x
= t x + 1. 2) (t 2x + 3) x
= 2t 4x + 1.
3) (t x + 4) x
+t +x 2 = 0. 4) (2t + 2x 1) x
+t +x + 1 = 0.
5) (t x 2) x
+t +x = 0. 6) (3t 7x 3) x
= 3x 7t + 7.
7) (3t + 2x 5) x
+ 2t + 3x 5 8) (4t + 2x + 1) x
+ 8t + 4x + 1 = 0.
9) (t 2x + 3) x
+ 2t +x 1 = 0. 10) (6t + 2x 10) x
= 2t + 9x 20.
R: 1) t
2
2tx x
2
+ 2t + 6x = C. 2) (1 3t + 6x)
10
9
e
4t2x
3
= C.
3) t
2
+ 2tx x
2
4t + 8x = C. 4) t + 2x + 3 ln [t +x 2[ = C.
5) x
2
2tx t
2
+ 4x = C. 6) (t +x 1)
5
(t x 1)
2
= C.
7) x
2
+ 3tx +t
2
5t 5x = C. 8) (4t + 2x + 1)
2
= 4t +C.
9) t
2
+tx x
2
t + 3x = C. 10) (x 2t)
2
= C (t + 2x 5).
13.17 Sa se integreze ecuat ia liniara neomogena x
= xtg t + cos t, t R
2
+n.
R: Ecuat ia omogena corespunzatoare, x
= xtg t, are solut ia generala x(t) = C

1
cos t
,
t R
2
+ n. Cautam pentru ecuat ia neomogena o solut ie particulara de forma
x
(t) = u(t)
1
cos t
. Se obt ine pentru u ecuat ia u
= cos
2
t, de unde u(t) =
1
2
t +
1
4
sin 2t.
In consecint a, solut ia generala a ecuat iei date este

x(t) = C
1
cos t
+ (
1
2
t +
1
4
sin 2t)
1
cos t
, t R
2
+n.
13.18 Sa se integreze urmatoarele ecuat ii liniare de ordinul ntai:
1) x
xctg t + 2t sin t = 0. 2)
_
1 +t
2
_
x
+x arctg t = 0.
3) x
+ax be
pt
= 0, a, b, p R. 4) tx
1
t+1
x t + 1 = 0.
5)
_
t
2
1
_3
2
x
t
3
+ 3tx
t
2
1 = 0. 6)
1 +t
2
x
+x +t
1 +t
2
= 0.
7) t
_
t
3
+ 1
_
x
+
_
2t
3
1
_
x =
t
3
2
t
. 8) x
n
t+1
x = e
t
(t + 1)
n
, n N.
R: 1) x(t) = t
2
sin t +C sin t. 2) x(t) = arctg t 1 +Ce
arctg t
.
3) x(t) =
b
a+p
e
pt
+Ce
at
, pentru p ,= a si x(t) = (bt +C) e
at
, pentru p = a.
4) x(t) = t + 1 +
C
t+1
e
t
. 5) x(t) =
1
4
_
C t
4
_ _
t
2
1
_
3
2
.
6) x(t) =
1
t+
1+t
2
_
ln
_
t +
1 +t
2
_
+C
_
.
7) x(t) =
1
t
+
Ct
t
3
+1
. 8) x(t) = (e
t
+C) (t + 1)
n
.
13.19 Sa se integreze urmatoarele ecuat ii liniare de ordinul ntai, cu condit iile init iale
precizate:
1) x
=
x
1t
2
t 1, cu x(0) = 0. 2) tx
+x = e
t
, cu x(a) = b (a ,= 0) .
3) tx
nx = t
n+1
ln t, cu x(1) = 0. 4) x
cos
2
t +x tg t = 0 cu x(0) = 0.
5) tx
nx = t
n+1
e
t
, cu x(1) = 1. 6) tx
+
_
2t
2
1
_
x = 2t
2
1, cu x(1) = 1
1
e
.
R: 1) x(t) =
_
1
2
t
1 t
2
+
1
2
arcsin t
_
_
1+t
1t
. 2) x(t) =
1
t
(e
t
e
a
+ab).
3) x(t) =
1
4
_
t
n
t
n+2
_
+
1
2
t
n+2
ln [t[. 4) x(t) = 1 + tg t +e
tg t
.
5) x(t) = t
n
(e
t
e + 1). 6) x(t) = 1 te
t
2
.
13.20 Sa se integreze urmatoarele ecuat ii diferent iale de tip Bernoulli:
1) tx
+x +t
t
x
2
= 0. 2) 2txx
x
2
+t = 0.
3) 3tx
= x
_
1 +t sin t 3x
3
sin t
_
. 4) x
= 2tx +t
3
x.
5) x
= tx tx
3
. 6) tx
+x = x
2
ln t.
7) 3tx
2
x
2x
3
= t
3
. 8) 2x
sin t +xcos t = x
3
sin
2
t.
R: 1) x
_
t
2
+Ct
_
= 1. 2) x
2
= t ln
C
t
. 3) x
3
(3 +Ce
cos t
) = t.
4) x =
_
Ce
t
2
2

t
2
+2
2
_
2
. 5)
_
1 +Ce
t
2
_
x
2
= 1. 6) x(1 +Ct + ln t) = 1.
7) x
3
= t
3
+Ct
2
. 8) x
2
(C t) sin t = 1.
13.21 Sa se integreze urmatoarele ecuat ii diferent iale de tip Bernoulli:
1) 3t
2
dt =
_
t
3
+e
x
_
dx. 2) txdt +
_
t
2
+x
2
+ 1
_
dx.
3) tx
+x = t
3
x
4
. 4)
_
t
2
ln x t
_
dx = xdt.
5) tx
+ 2x = 3t
3
x
4
3
. 6) x
2t
1+t
2
x = 4
1+t
2
arctg t.
R: 1) t
3
e
x
= x +C. 2) x
4
+ 2t
2
x
2
+ 2x
2
= C. 3) tx
3
_
3 ln
C
t
= 1.
4) t (1 Cx + ln x) = 1. 5) x
1
3
= Ct
2
3

3
7
t
3
. 6) x(t) =
_
1 +t
2
_ _
C + arctg
2
t
_
2
.
13.22 Sa se integreze urmatoarele ecuat ii diferent iale de tip Bernoulli, cu condit iile
init iale precizate:
1) x
+x = e
t
2
x, cu x(0) =
9
4
.
2)
_
t
3
+ 1
_
x
+ 3t
2
x = x
2
_
t
3
+ 1
_
2
sin t, cu x(0) = 1.
3)
_
x
2
+ 2x +t
2
_
x
+ 2t = 0, cu x(1) = 0.
4) 2
_
t
2
1
_
xx
tx
2
= t
_
t
2
1
_
, cu x
_
2
_
=
2.
5) x
xcos t = x
n1
sin 2t, n ,= 1, n N 1, 2 , cu x() = 1.
R: 1) x(t) = e
t
_
1
2
e
t
+ 1
_
2
. 2) x(t) =
1
(t
3
+1) cos t
. 3) t
2
+x
2
= e
x
.
4) x
2
= t
2
1 +
t
2
1. 5) x
1n
= 2 sin t +
2
n1
+
n3
n1
e
(n1) sin t
.
13.23 Sa se arate ca ecuat iile diferent iale de tip Riccati de forma t
2
x
= at
2
x
2
+btx+c,
a, b, c R, admit solut ii particulare de forma x
(t) = t
1
, daca (b + 1)
2
4ac 0.
Sa se integreze apoi ecuat iile diferent iale:
1) 2t
2
x
= t
2
x
2
+ 1. 2) 4t
2
_
x
+x
2
_
+ 1 = 0.
3) t
2
x
+ (2 tx)
2
= 0. 4) t
2
x
= t
2
x
2
+tx + 1.
R:

Intr-adevar, x
(t) = t
1
este solut ie daca a
2
+ (b + 1) + c = 0, ecuat ie care
are radacini reale daca (b + 1)
2
4ac 0. 1) O solut ie particulara este x
(t) = t
1
.
Efectuand schimbarea de funct ie x =
1
t
+
1
y
, obt inem ecuat ia liniara 2t
2
y
= 2ty t
2
,
a carei solut ie generala este: y (t) =
t
2
(C ln t). Deci, x(t) =
1
t
+
2
t(Cln|t|)
.
2) x(t) =
1
2t
+
1
t(C+ln|t|)
. 3) x(t) =
1
t
+
3t
2
t
3
+C
. 4) x(t) =
1
t
+
1
t(Cln|t|)
.
13.24 Sa se integreze urmatoarele ecuat ii diferent iale de tip Riccati, stiind ca admit
solut iile particulare indicate:
1) x
x
2
+ 2e
t
x = e
t
+e
2t
, x
(t) = e
t
.
2) tx
x
2
+ (2t + 1) x = t
2
+ 2t, x
(t) = t.
3) x
+x
2
sin t = 2
sin t
cos
2
t
, x
(t) =
1
cos t
.
4)
_
t
2
1
_
x
+x
2
2tx + 1 = 0, x
(t) = t.
5) t
2
x
+t
2
x
2
+tx = 4, x
(t) =
2
t
.
6)
_
1 +t
3
_
x
x
2
t
2
x = 2t, x
(t) = t
2
.
7) x
x
2
1
t
x + 9t
2
= 0, x
(t) = 3t.
8) t
2
_
x
+x
2
_
2 (tx 1) = 0, x
(t) =
2
t
.
R: 1) x(t) = e
t
+
1
Ct
. 2) x(t) = t +
1
Ct+1
. 3) x(t) =
1
cos t
+
3 cos
2
t
3Ccos
3
t
.
4)
1
xt
=
1
2
ln
t1
t+1
+C. 5) x(t) =
2
t
+
4
Ct
5
t
. 6) x(t) = t
2
+
1+t
3
Ct
.
7) x(t) = 3t +
t
6Ce
3t
2
1
. 8) x(t) =
2
t
+
1
t(Ct1)
.
13.25 Sa se integreze urmatoarele ecuat ii diferent iale de tip Riccati, stiind ca admit
solut iile particulare de forma x
(t) = t
n
, R, n N:
1) t (2t 1) x
+x
2
+ (4t + 1) x + 4t = 0. 2)
_
t
5
1
_
x
+ 2tx
2
t
4
x 3t
2
= 0.
R: 1) n = 1, = 2, x(t) =
4Ct
3
1
Ct
4
t
. 2) n = 3, = 1, x(t) =
Ct
3
1
t
2
C
.
13.2 Alte ecuat ii integrabile prin metode elementare
13.26 Sa se integreze ecuat ia x = a
n
(x
)
n
+a
n1
(x
)
n1
+ +a
1
x
+a
0
.
R: Punem x
= p. Atunci dx = p dt, dt =
1
p
dx, de unde
t =
_
1
p
(na
n
p
n1
+ (n 1)a
n1
p
n2
+ +a
1
) dp.
Solut ia generala este data de
_
t =
n
n1
a
n
p
n1
+
n1
n2
a
n1
p
n2
+ +a
2
p +a
1
ln p +C,
x = a
n
p
n
+a
n1
p
n1
+ +a
1
p +a
0
, p > 0.
13.27 Sa se integreze ecuat ia x = (x
)
2
tg x
.
R: t = ptg p ln (cos p) +C, x = p
2
tg p.
13.28 Sa se integreze ecuat iile:
1) x
2
3
+ (x
)
2
3
= 1. 2) x
2
5
+ (x
)
2
5
= a
2
5
, a ,= 0.
R: 1) Luam x = cos
3
si x
= sin
3
. Rezulta t = 3 + 3tg + C, x = cos
3
. 2)
Luam x = a sin
5
si x
= a cos
5
. Rezulta t = 5
_
1
3
tg
3
tg +
_
+C, x = a sin
5
.
1) t = 2x
+e
x
. 2) t = x
sin x
+ cos x
.
3) t =
_
2 (x
)
2
2x
+ 1
_
e
2x
. 4) t = x
sin x
.
R: 1) Punem x
= p. Atunci t = 2p +e
p
, dx = p dt = (2p +pe
p
) dp. Solut ia generala
este data de
t = 2p +e
p
, x = p
2
+ (p 1)e
p
+C.
2) t = p sin p + cos p, x =
_
p
2
2
_
sin p + 2p cos p +C.
3) t =
_
2p
2
2p + 1
_
e
2p
, x =
_
2p
3
3p
2
+ 3p
3
2
_
e
2p
+C.
4) t = p sin p, x =
_
p
2
1
_
sin p +p cos p +C.
13.30 Sa se integreze ecuat ia Lagrange x = 2tx
+ (x
)
2
.
R: Punem x
= p. Atunci x = 2tp + p
2
si diferent iem: dx = 2p dt + 2t dp + 2p dp.
Dar dx = p dt si deci
dt
dp
=
2
p
t 1, care este o ecuat ie liniara, a carei solut ie generala,
pentru p ,= 0, este t =
C
p
2

p
3
, ncat solut ia generala a ecuat iei date se scrie
t =
C
p
2

p
3
, x =
2C
p
+
p
2
3
, p R 0.
Pentru p = 0 se obt ine x(t) 0, care este o solut ie singulara.
13.31 Sa se integreze ecuat ia Clairaut x = tx
+ (x
)
n
.
R: Punem x
= p si derivand obt inem: p = tp
+ p +np
n1
p
sau p
(t + np
n1
) = 0.
Avem: p
= 0, p = C, care da solut ia generala x(t) = Ct + C

n
. Sau t = np
n1
,
x = (1 n)p
n
, care reprezinta o integrala singulara.
13.32 Sa se integreze urmatoarele ecuat ii de tip Lagrange sau Clairaut:
1) x = 2tx
+ ln x
. 2) x = t (1 +x
) + (x
)
2
. 3) x = 2tx
+ sin x
.
4) x =
3
2
tx
+e
x
. 5) x = 2t + (x
)
2
4x
. 6) x = (x
)
3
+t (x
)
2
.
7) x = (x
)
2
+t (x
)
2
. 8) x = tx
+
_
1 + (x
)
2
. 9) x = 1 +tx
+ (x
)
2
.
10) x = 2tx
4 (x
)
3
. 11) x = tx
+x
(1 x
) . 12) t (x
)
2
xx
= 1.
R: 1) t =
C
p
2

1
p
, x + ln p +
2C
p
2, p > 0.
2) t = 2 (1 p) +Ce
p
, x = [2 (1 p) +Ce
p
] (1 +p) +p
2
.
3) t =
C
p
2

cos p
p
2

sin p
p
, x =
2C
p

2 cos p
p
sin p, p ,= 0 si x = 0, solut ie singulara.
4) t =
C
p
3
2e
p
_
1
p

2
p
2
+
2
p
3
_
, x =
3C
2p
2
2e
p
_
1
3
p
+
3
p
2
_
, p ,= 0.
5) t = 2p +C, x = p
2
+ 2C si x = 2t 4, solut ie singulara.
6) t =
1
(p1)
2
_
C p
3
+
3
2
p
2
_
, x =
p
2
(p1)
2
_
C +p
p
2
2
_
si x = 0, x = t + 1, solut ii
singulare.
7) t =
1
(p1)
2
1, x =
Cp
2
(p1)
2
si x = 0, x = t + 1, solut ii singulare.
8) x = Ct +
1 +C
2
si t
2
+x
2
= 1, solut ie singulara.
9) x = Ct + 1 +C
2
si t = 2p, x = 1 p
2
, solut ie singulara.
10) t = 3p
2
+Cp
2
, x = 2p
3
2Cp
1
, p ,= 0 si x = 0, solut ie singulara.
11) x = Ct +C (1 C) si t = 2p 1, x = p
2
, solut ie singulara.
12) t = Cx +C
2
si x
2
+ 4t = 0, solut ie singulara.
1) xx
+ (t x) x
t = 0. 2) (x
)
2
(2x +t) x
+ 2tx = 0.
R: 1) Ecuat ia se mai scrie: t (x
1) +xx
(x
1) = 0, deci x
= 1 sau t = xx
. De
unde: x = t +C
1
sau x
2
+t
2
= C
2
.
2) Ecuat ia se mai scrie: t (x
2x) = x
(x
2x), deci x
= 2x sau x
= t. De unde
x = C
1
e
2t
sau x =
1
2
t
2
+C
2
.
13.34 Sa se integreze ecuat ia (x
)
2
+tx
+ 3x +t
2
= 0.
R: Punem x
= p, avem p
2
+ tp + 3x + t
2
= 0. Derivam n raport cu t: 2pp
+ p +
tp
+ 3p + 2t = 0 sau (2p + 1)(p
+ 2) = 0. Din p
= 2 urmeaza p = 2t + C, de unde
solut ia generala
x(t) =
1
3
[t
2
+t(C 2t) + (C 2t)
2
], t R.
Apoi t = 2p si x = p
2
13.35 Sa se integreze ecuat ia t =
1
x
x + (x
)
n
.
R: Punem x
= p, avem t =
1
p
x+p
n
. Derivamn raport cu x. Obt inem
dp
dx
(np
n1
1
p
2
) = 0. Deci
dp
dx
= 0, p = C, de unde solut ia generala t(x) =
1
C
x +C
n
, sau x = np
n+1
,
t = (n + 1)p
n
13.3 Ecuat ii diferent iale de ordin superior
13.36 Sa se gaseasc a solut ia ecuat iei x
(5)
= 0, care satisface condit iile init iale:
x(0) = 1, x
(0) = 0, x
(0) = 1, x
(3)
(0) = 0, x
(4)
(0) = 1.
R: Solut ia generala este x(t) =
C
1
4!
t
4
+
C
2
3!
t
3
+
C
3
2!
t
2
+
C
4
1!
t + C
5
. Condit iile init iale
precizate conduc la solut ia particulara x(t) =
1
24
t
4
1
2
t
2
+ 1, t R.
13.37 Sa se gaseasc a solut ia generala a ecuat iei x
=
1
t
.
R: x(t) = t ln [t[ +C
1
t +C
2
.
13.38 Sa se determine solut ia ecuat iei x
= sin t, care satisface condit iile init iale

x(0) = 1, x
(0) = 1, x
(0) = 0.
R: Prin trei integrari succesive obt inem solut ia generala x(t) = cos t+
1
2
C
1
t
2
+C
2
t+C
3
.
Solut ia problemei lui Cauchy este x(t) = cos t +t
2
t.
13.39 Sa se gaseasc a solut ia generala a ecuat iei t = x
+ ln x
.
R: Punem x
= . Atunci t = + ln . Avem dx
= dt = (1 +
1
) . Se obt ine
solut ia generala t = + ln , x =
1
6
3
+
3
4
2
+C
1
( + ln ) +C
2
.
13.40 Sa se gaseasc a solut ia generala a ecuat iei t = e
x
(x
)
2
.
R: Punem x
= . Atunci t = e

2
. Avem dx
= dt = (e
2) d. De unde
x
= e
2
3
3
+ C
1
. Apoi dx = x
dt =
_
e
2
3
3
+C
1
_
(e
2) d. De
unde
x =
_
1
2

3
4
_
e
2
+
_
2 2
2
3
3
+C
1
_
e
+
4
15
5
C
1
2
+C
2
.
13.41 Sa se integreze ecuat iile: 1) x
= 1 (x
)
2
. 2) (x
)
2
+ (x
)
2
= 1. 3) (x
)
2
=
2x
.
R: 1) O reprezentare parametrica a ecuat iei este: x
= , x
= 1
2
. Din dx
= d
si dx
=
_
1
2
_
dt, obt inem dt =
1
1
2
d. Deci t =
1
2
ln
1+
1
+ C
1
. Din dx = dt =
1
2
d, de unde x =
1
2
ln
1
2
+C
2
.
2) O reprezentare parametrica a ecuat iei este: x
= cos , x
= sin . Din dx
=
sin d si dx
= sin dt, rezulta dt = d, deci t = + C

1
. Din dx
= cos dt =
cos d, urmeaza x
= sin + C
2
, iar din dx = (sin +C
2
) dt = (sin C
2
) d,
deducem x = cos C
2
+C
3
.
3) Luam x
= 2. Atunci x
= 2
2
. Din dx
= 4 d si dx
= 2 dt, rezulta
dt = 2 d, deci t = 2 + C
1
. Din dx
= 2
2
dt = 4
2
d, urmeaza x
=
4
3
3
+ C
2
, iar din
dx =
_
4
3
3
+C
2
_
dt = 2
_
4
3
3
+C
2
_
d, deducem x =
2
3
4
+ 2C
2
+C
3
.
13.42 Sa se integreze ecuat ia x
(3)
x
(4)
= 1.
R: O reprezentare parametrica este x
(3)
= , x
(4)
=
1
, ,= 0. Obt inem dx
(3)
= d,
dx
(3)
=
1
dt, deci dt = d. Se obt ine solut ia generala

t =
1
2
2
+C
1
, x =
1
105
7
+
1
8
C
1
1
2
C
2
2
+C
3
.
13.4 Ecuat ii carora li se poate micsora ordinul
(n)
sin t x
(n1)
cos t + 1 = 0.
R: Punem x
(n1)
= u si ecuat ia se transforma ntr-o ecuat ie liniara n u: u
sint
ucos t +1 = 0. Cu solut ia u(t) = cos t +C
1
sin t. Deci x
(n1)
= cos t +C
1
sin t, cu solut ia
generala:
x(t) = cos
_
t
n 1
2

_
+C
1
sin
_
t
n 1
2

_
+
C
2
(n 2)!
t
n2
+ +
C
n1
1!
t +C
n
.
13.44 Sa se integreze ecuat ia xx
(x
)
2
= x
2
.
R: Ecuat ia nu cont ine pe t explicit. Punem x
= u, x
= u
du
dx
si obt inem ecuat ia
xu
du
dx
= u
2
+ x
2
, care este o ecuat ie omogena. Luand u = xy, obt inem y dy =
1
x
dx, de
unde y
2
= 2 ln [x[ +C
1
, deci x
= x
2 ln x +C
1
, cu solut ia x = e
1
2
((tC
2
)
2
C
1)
.
13.45 Sa se integreze ecuat iile: 1) txx
+t (x
)
2
xx
= 0. 2) t
2
xx
= (x tx
)
2
.
R: Ecuat iile sunt omogene n x, x
, x
. 1) Cu schimbarea de funct ie
x
x
= u, obt inem
x
= xu, x
= x(u
2
+u
) si deci ecuat ia devine tu
u+2tu
2
= 0. Rezulta x = C
2
t
2
+C
1
.
2) x = C
2
te
C
1
t
.
13.46 Sa se integreze ecuat ia t
2
xx
+t
2
(x
)
2
5txx
+ 4x
2
= 0.
R: Ecuat ia este omogena de ordinul patru n t, x, dt, dx, d
2
x.

Impart ind prin t
2
se
poate pune sub forma
x
t
tx
+ (x
)
2
5
x
t
x
+ 4
_
x
t
_
2
= 0. Punem t = e
, x = tu
si ecuat ia devine uu
+ (u
)
2
2uu
= 0. Luand acum u
= p obt inem ecuat ia liniara

dp
du
+
1
u
p 2 = 0, cu solut ia p (u) =
1
u
_
u
2
+C
1
_
. Deci u
=
1
u
_
u
2
+C
1
_
. De unde
u
2
() = C
2
e
2
C
1
. Rezulta x
2
= t
2
_
C
2
t
2
C
1
_
.
Capitolul 14
Ecuat ii si sisteme diferent iale
liniare
14.1 Sisteme diferent iale liniare de ordinul ntai
14.1 Se da sistemul:
x
=
3
t
x
1
t
y, y
=
1
t
x
1
t
y, t > 0.
Sa se verice ca:
x
1
=
1
t
2
, y
1
=
1
t
2
, x
2
=
1
t
2
ln t, y
2
=
1
t
2
(1 + ln t),
formeaz a un sistem fundamental de solut ii si sa se scrie solut ia generala a sistemului.
R: Solut ia generala este:
x(t) =
1
t
2
(C
1
+C
2
ln t) , y(t) =
1
t
2
(C
1
ln t +C
2
(1 + ln t)) .
x
=
1
t
x +
1
t
y, y
=
4
t
x +
3
t
y + 2, t > 0.
Sa se verice ca:
x
1
= t, y
1
= 2t, x
2
= t ln t, y
2
= t(1 + 2 ln t),
R: O solut ie particulara a sistemului este: x
(t) = t ln
2
t, y
(t) = 2t(ln
2
t + ln t).
179
CAPITOLUL 14. ECUAT II SI SISTEME DIFERENT IALE LINIARE 180
tx
= x +y, ty
= y +
t
(t + 1)
2
ln(t + 1), t > 0.
Sa se verice ca:
x
1
= t, y
1
= 0, x
2
=
1
t
, y
2
=
2
t
,
R: O solut ie particulara a sistemului este: x
= ln(t + 1), y
=
t
t+1
ln(t + 1).
x
=
4
t
x
4
t
2
y +
1
t
, y
= 2 x
1
t
y +t, t (0, ).
Sa se verice ca: x
1
(t) = 1, y
1
(t) = t si x
2
(t) = 2t
2
, y
2
(t) = t
3
, t (0, ), formeaza un
sistem fundamental de solut ii si sa se scrie solut ia generala a sistemului.
R: Deoarece W(t) = t
3
,= 0, cele doua solut ii formeaza un sistem fundametal de
solut ii pentru sistemul dat si deci solut ia generala a sistemului omogen corespunzator
este
x(t) = C
1
+ 2C
2
t
2
, y(t) = C
1
t +C
2
t
3
.
Cautam pentru sistemul neomogen o solut ie particulara de forma
x
(t) = u(t) + 2t
2
v(t), y(t) = t u(t) +t
3
v(t).
Derivand si nlocuind n sistem, obt inem
u
+ 2t
2
v
=
1
t
, u
+t
3
v
= t,
sau, rezolvand n privint a lui u
si v
:
u
= 2
1
t
, v
=
1
t
2
+
1
t
3
,
de unde, prin integrare u(t) = 2t ln t, v(t) =
1
t

1
2t
2
.

Inlocuind n x
(t) si y
(t),
obt inem solut ia particulara a sistemului neomogen
x
(t) = 4t 1 ln t, y
(t) = 3t
2
1
2
t t ln t
si deci solut ia generala a sistemului neomogen este
x(t) = C
1
+ 2C
2
t
2
+ 4t 1 ln t, y(t) = C
1
t +C
2
t
3
+ 3t
2
1
2
t t ln t, t > 0.
14.2 Sisteme diferent iale liniare cu coecient i con-
stant i
14.5 Sa se determine solut ia generala a sistemului diferent ial liniar omogen cu coeci-
ent i constant i:
x
= 3y 4z, y
= z, z
= 2x +y.
R: Matricea transformarii liniare asociate este
A =
_
_
0 3 4
0 0 1
2 1 0
_
_
.
Ecuat ia caracteristica a transformarii liniare T este
3
76 = 0, cu radacinile
1
= 1,
2
= 2,
3
= 3, simple. Deci transformarea T poate adusa la expresia canonica.
Vectorii proprii corespunzatori sunt
u
1
= (1, 1, 1), u
2
= (5, 2, 4), u
3
= (5, 1, 3).
Deci funct iile
x
1
(t) = e
t
(1, 1, 1), x
2
(t) = e
2t
(5, 2, 4), x
3
(t) = e
3t
(5, 1, 3)
formeaza un sistem fundamental de solut ii. Solut ia generala a sistemului se scrie atunci
_
_
_
x(t) = C
1
e
t
+ 5C
2
e
2t
+ 5C
3
e
3t
,
y(t) = C
1
e
t
+ 2C
2
e
2t
+ C
3
e
3t
, t R.
z(t) = C
1
e
t
+ 4C
2
e
2t
3C
3
e
3t
,
14.6 Sa se determine solut ia general a a sistemului
x
= y, y
= x.
R: Ecuat ia caracteristica este
2
+ 1 = 0 si deci
1
= i,
2
= i, iar vectorii proprii
corespunzatori u
1
= (1, i), u
2
= (1, i). Un sistem fundamental de solut ii (complexe) va
x
1
(t) = (e
it
, ie
it
), x
2
(t) = (e
it
, ie
it
).
Prin schimbarea precedenta, obt inem sistemul fundamental de solut ii (reale)
y
1
(t) = (cos t, sint), y
2
(t) = (sin t, cos t),
ncat, solut ia generala a sistemului diferent ial dat se va scrie
x(t) = C
1
cos t +C
2
sin t, y(t) = C
1
sint +C
2
cos t.
14.7 Sa se determine solut iile generale ale sistemelor:
1)
_
x
= x +y,
y
= x y.
2)
_
x
= 3x + 8y,
y
= x 3y.
R: Avem:
1) x(t) = C
1
e
t
2
+C
2
e
t
2
, y (t) = C
1
_
2 1
_
e
t
2
C
2
_
2 + 1
_
e
t
2
.
2) x(t) = 4C
1
e
t
2C
2
e
t
, y (t) = C
1
e
t
+C
2
e
t
.
14.8 Sa se determine solut ia sistemului: x
= 2x + y, y
= x + 2y, care satisface

condit iile init iale: x(0) = 1, y (0) = 3.
R: x(t) =
1
e
3t
e
t
, y (t) = 2e
3t
+e
t
.
14.9 Sa se determine solut ia general a a sistemului x
= y, y
= x + 2y.
R: Ecuat ia caracteristica este ( 1)
2
= 0 si deci
1
= 1, cu m
1
= 2, iar vectorul
propriu corespunzator u
1
= (1, 1). Transformarea liniara T nu poate adusa la expresia
canonica. Cautam atunci solut ia generala sub forma x(t) = (a +bt)e
t
, y(t) = (c +dt)e
t
.
Derivand si nlocuind n sistem, obt inem pentru a, b, c, d sistemul: a + b = c, b = d,
a c + d = 0, b 2c + d = 0, care este compatibil dublu nedeterminat. Luand a = C
1
,
b = C
2
, gasim c = C
1
+C
2
, d = C
2
a.. solut ia generala va
x(t) = (C
1
+C
2
t)e
t
, y(t) = (C
1
+C
2
+C
2
t)e
t
.
14.10 Sa se rezolve sistemul liniar: x
= Ax, n care:
A =
_
_
2 1 0
1 0 2
0 1 2
_
_
.
R: Valorile proprii ale matricei A sunt:
1
= 2, m
1
= 1, u
1
= (2, 0, 1),
2
= 1, m
2
= 2,
u
2
= (1, 1, 1). O solut ie a sistemului este x
1
(t) = (2, 0, 1)e
2t
. Corespunzator valorii
proprii
2
= 1, m
2
= 2, cautam o solut ie de forma: x(t) = (a
1
+b
1
t, a
2
+b
2
t, a
3
+b
3
t)e
t
.
Se obt ine prin identicare: x(t) = (C
2
+C
3
t, C
2
C
3
+C
3
t, C
2
+C
3
t)e
t
. Solut ia generala
este:
_
_
_
x(t) = 2C
1
e
2t
+ (C
2
+C
3
t)e
t
,
y(t) = (C
2
C
3
+C
3
t)e
t
,
z(t) = C
1
e
t
+ (C
2
+C
3
t)e
t
.
14.11 Sa se rezolve sistemele de ecuat ii diferent iale omogene:
1)
_
x
= 2x +y,
y
= x + 4y.
2)
_
x
= x 5y,
y
= 2x y.
3)
_
x
= 5x y,
y
= x + 3y.
R: 1)
2
6 + 9 = 0,
1
= 3, m
1
= 2. Cautam solut ia sub forma:
x(t) = (a
1
+b
1
t, a
2
+b
2
t)e
3t
. Se obt ine:
x(t) = (C
1
+C
2
t)e
3t
, y(t) = (C
1
+C
2
+C
2
t)e
3t
.
2)
2
+ 9 = 0,
1
= 3i,
2
= 3i. Se obt in solut iile complexe:
x
1
(t) =
_
1
2
+
3
2
i, 1
_
e
3it
, x
2
(t) =
_
1
2

3
2
i, 1
_
e
3it
.
Dar:
_
1
2
(x
1
(t) +x
2
(t)) =
_
1
2
cos 3t
3
2
sin 3t, cos 3t
_
,
1
2i
(x
1
(t) x
2
(t)) =
_
1
2
cos 3t +
3
2
sin 3t, sin 3t
_
,
sunt solut ii liniar independente
reale.
Deci:
_
x(t) = C
1
_
1
2
cos 3t
3
2
sin 3t
_
+C
2
_
3
2
cos 3t +
1
2
sin 3t
_
,
y(t) = C
1
cos 3t +C
2
sin 3t.
3) x(t) = (C
1
+C
2
+C
2
t) e
4t
, y (t) = (C
1
+C
2
t) e
4t
.
1)
_
x
= 4x 3y,
y
= 3x + 4y.
2)
_
x
= 12x 5y,
y
= 5x + 12y.
3
_
x
= x 5y,
y
= 2x y.
R: Avem:
1) x(t) = (C
1
cos 3t C
2
sin 3t) e
4t
, y (t) = (C
1
sin 3t +C
2
cos 3t) e
4t
.
2) x(t) = (C
1
cos 5t C
2
sin 5t) e
12t
, y (t) = (C
1
sin 5t +C
2
cos 5t) e
12t
.
3) x(t) = C
1
cos 3t + (5C
2
3C
1
) sin 3t, y (t) = C
2
sin 3t + (2C
1
3C
2
) cos 3t.
1)
_
_
_
x
= 3x y +z,
y
= x + 5y z,
z
= x y + 3z.
2)
_
_
_
x
= 2x +y,
y
= x + 3y z,
z
= x + 2y + 3z.
3)
_
_
_
x
= x +y +z,
y
= x y +z,
z
= x +y +z.
R: 1)
3
11
2
+ 36 36 = 0,
1
= 2,
2
= 3,
3
= 6. Se obt ine:
_
_
_
x(t) = C
1
e
2t
+C
2
e
3t
+C
3
= C
1
e
2t
+C
2
e
3t
+C
3
e
6t
,
y(t) = C
2
e
3t
2C
3
e
6t
,
z(t) = C
1
e
2t
+C
2
e
3t
+C
3
e
6t
.
2)
3
8
2
+ 22 20 = 0, valorile proprii: 2, 3 +i, 3 i si deci:
_
_
_
x
1
(t) = (1, 0, 1) = (1, 0, 1) e
2t
,
x
2
(t) = (1, 1 +i, 2 i)e
(3+i)t
,
x
3
(t) = (1, 1 i, 2 +i)e
(3i)t
.
Solut ia reala este:
_
_
_
x(t) = C
1
e
2t
+ (C
2
cos t +C
3
sin t)e
3t
,
y(t) = (C
2
(cos t sin t) +C
3
(cos t + sin t)) e
3t
,
z(t) = C
1
e
2t
+ (C
2
(2 cos t + sin t) C
3
(cos t 2 sin t)) e
3t
.
3)
_
_
_
x(t) = C
1
e
2t
C
2
e
2t
+C
3
e
t
,
y (t) = C
1
e
2t
+C
2
e
2t
+C
3
e
t
,
z (t) = 2C
1
e
2t
C
3
e
t
.
1)
_
_
_
x
= 2y,
y
= 2z,
z
= 2x.
2)
_
_
_
x
= y +z,
y
= z +x,
x
= x +y.
3)
_
_
_
x
= 6x 12y z,
y
= x 3y z,
z
= 4x + 12y + 3z.
R: Avem:
1)
_
_
_
x(t) = C
1
e
t
sin t
3 +C
2
e
t
cos t
3 +C
3
e
2t
,
y (t) =
1
2
_
C
1
+C
2
3
_
e
t
sint
3 +
1
2
_
C
1
3 C
2
_
e
t
cos t
3 +C
3
e
2t
,
z (t) =
1
2
_
C
1
C
2
3
_
e
t
sin t
3
1
2
_
C
1
3 +C
2
_
e
t
cos t
3 +C
3
e
2t
.
2) x(t) = C
1
e
t
+C
2
e
2t
, y (t) = (C
1
+C
3
) e
t
+C
2
e
2t
, z (t) = C
2
e
2t
+C
3
e
t
.
3)
_
_
_
x(t) = 2C
1
e
t
+
7
3
C
2
e
2t
+ 3C
3
e
3t
,
y (t) = C
1
e
t
+C
2
e
2t
+C
3
e
3t
,
z (t) = 2C
1
e
t
8
3
C
2
e
2t
3C
3
e
3t
.
14.15 Sa se rezolve sistemul omogen, cu condit iile init iale precizate:
_
_
_
x
= 8y,
y
= 2z,
z
= 2x + 8y 2z,
_
_
_
x(0) = 4,
y (0) = 0,
z (0) = 1.
R: x(t) = 4e
2t
2 sin 4t, y (t) = e
2t
cos 4t, z (t) = e
2t
2 sin 4t.
14.16 Sa se determine solut ia generala a sistemelor de ecuat ii diferent iale liniare neo-
mogene:
1)
_
x
= 2x +y + 2e
t
,
y
= x + 2y + 3e
4t
.
2)
_
x
= 2x + 4y + cos t,
y
= x 2y + sin t.
R: Avem:
1) x(t) = C
1
e
t
+C
2
e
3t
+te
t
e
4t
, y(t) = C
1
e
t
+C
2
e
3t
(t + 1)e
t
2e
4t
.
2) x(t) = C
1
t +C
2
+ 2 sin t, y(t) = 2C
1
t C
1
2C
2
3 sin t 2 cos t.
14.17 Sa se determine solut ia problemei lui Cauchy pentru sistemul:
x
= x +y, y
= 2x + 4y,
cu condit iile init iale: x(0) = 0, y(0) = 1.
R: x(t) = (1 t) cos t sin t, y(t) = (t 2) cos t +t sin t.
14.18 Sa se determine solut ia generala a sistemelor diferent iale liniare cu coecient i
constant i:
1)
_
x
= y + 1,
y
= x + 1.
2)
_
x
= 2x 4y + 1 + 4t,
y
= x +y +
3
2
t
2
.
3)
_
x
= 3x
1
2
y 3t
2
1
2
t +
3
2
,
y
= 2y 2t 1.
R: Avem:
1) x(t) = C
1
e
t
+C
2
e
t
1, y(t) = C
1
e
t
C
2
e
t
1.
2) x(t) = C
1
e
2t
+ 4C
2
e
3t
+t +t
2
, y(t) = C
1
e
2t
+C
2
e
3t
1
2
t
2
.
3) x(t) = C
1
e
2t
+C
2
e
3t
+t +t
2
, y(t) = 2C
1
e
2t
+ 1 +t.
constant i:
1)
_
x
= 4x + 6y,
y
= 2x + 3y +t.
2)
_
x
= y +e
3t
,
y
= x + 2e
3t
.
R: Avem:
1) x(t) =
3
2
C
1
+ 2C
2
e
7t
3
7
t
2
6
49
t
6
343
, y (t) = C
1
+C
2
e
7t
3
49
t +
2
7
t
2
3
343
.
2) x(t) = C
1
e
t
+C
2
e
t
+
1
8
e
3t
, y (t) = C
1
e
t
+C
2
e
t
+
5
8
e
3t
.
14.20 Sa se rezolve urmatoarele sisteme, cu condit iile init iale precizate:
1)
_
x
= 2x +y,
y
= x + 2y,
_
x(0) = 1,
y (0) = 3.
2)
_
x
= 3x + 8y,
y
= x 3y,
_
x(0) = 6,
y (0) = 2.
R: Avem:
1) x(t) = 2e
3t
e
t
, y (t) = 2e
3t
+e
t
.
2) x(t) = 4e
t
+ 2e
t
, y (t) = e
t
e
t
.
14.21 Sa se rezolve urmatoarele sisteme, cu condit iile init iale precizate:
1)
_
x
= y +t,
y
= x +e
t
,
_
x(0) = 1,
y (0) = 0.
2)
_
x
= 3x y + sin t,
y
= 4x + 3y + cos t,
_
x(0) = 1,
y (0) = 1.
R: Avem:
1) x(t) =
3
4
e
t
+
5
4
e
t
1 +
1
2
e
t
t, y (t) =
5
4
e
t
5
4
e
t
+
1
2
e
t
t t.
2) x(t) =
9
26
cos t
3
13
sin t +
75
104
e
5t
+
5
8
e
t
, y (t) =
21
26
cos t
1
26
sin t
75
52
e
5t
+
5
4
e
t
.
constant i:
1)
_
_
_
x
= 2x +y 2z t + 2,
y
= x + 1,
z
= x +y z + 1 t.
2)
_
_
_
x
= 4x + 2y + 5z + 4t 2e
t
4,
y
= 6x y 6z 6t 6,
z
= 8x + 3y + 9z 3e
t
+ 8t 9.
R: Avem:
1)
_
_
_
x(t) = C
1
e
t
+C
2
sin t +C
3
cos t,
y(t) = C
1
e
t
+C
2
cos t C
3
sin t +t,
z(t) = C
2
sin t +C
3
cos t + 1.
2)
_
_
_
x(t) = C
1
e
2t
+ (C
2
t +C
2
+C
3
)e
t
+t,
y(t) = 2C
1
e
2t
+ 3C
2
e
t
+e
t
,
z(t) = 2C
1
e
2t
+ (C
2
t +C
3
) e
t
+ 1.
14.3 Ecuat ii diferent iale liniare de ordinul n
14.23 Se da ecuat ia diferent iala liniara omogen a de ordinul al doilea:
x
+a
1
(t)x
+a
2
(t)x = 0, t I.
Sa se arate ca daca
_
x
1
(t), x
2
(t)
_
formeaz a un sistem fundamental de solut ii al carui
wronskian este W(t), atunci W este solut ie a ecuat iei diferent iale: W
+ a
1
(t)W = 0 si
sa se deduca formula lui Abel - Ostrogradski - Liouville:
W(t) = W(t
0
) exp
_
_
t
t
0
a
1
(t)dt
_
, t
0
I.
Generalizare.
R: Avem:
_
x
i
_
+a
1
(t)
_
x
i
_
+a
2
(t)x
i
= 0, pentru i = 1, 2. Dar,
W
(t) =
d
dt
x
1
x
2
_
x
1
_
_
x
2
_
x
1
x
2
a
1
_
x
1
_
a
1
_
x
2
_
= a
1
(t)W(t).
14.24 Se da sistemul de funct ii liniar independente
_
x
1
(t), x
2
(t)
_
. Sa se arate ca ecuat ia
diferent ial a liniara omogena a carei solut ie generala este:
x(t) = C
1
x
1
(t) +C
2
x
2
(t),
cu C
1
si C
2
constante arbitrare, este:
x
1
(t) x
2
(t) x
_
x
1
(t)
_
_
x
2
(t)
_
_
x
1
(t)
_
_
x
2
(t)
_
= 0.
Generalizare.
R: Derivand x(t) de doua ori, prin eliminarea lui C
1
si C
2
ntre cele trei relat ii se
obt ine ecuat ia din enunt .
14.25 Sa se formeze ecuat ia diferent iala omogena al carui sistem fundamental de solut ii
este:
1) x
1
= sin t, x
2
= cos t.
2) x
1
= e
t
, x
2
= te
t
.
3) x
1
= t, x
2
= t
2
.
4) x
1
= e
t
, x
2
= e
t
sin t, x
3
= e
t
cos t.
R: 1) x
+x
= 0. 2) x
2x
+x = 0. 4) x
2tx
+2x = 0. 4) x
3x
4x
2x = 0.
14.26 Sa se arate ca ecuat ia diferent iala x
+ a
2
x = 0, a R 0 admite solut iile
x
1
(t) = cos at, x
2
(t) = sin at si sa se scrie solut ia generala.
R: Wronskianul sistemului
_
x
1
(t), x
2
(t)
_
este
W(t) =
cos at sin at
a sin at a cos at
= a ,= 0.
Deci
_
x
1
(t), x
2
(t)
_
formeaza un sistem fundamental de solut ii pentru ecuat ia data, iar
solut ia ei generala este
x(t) = C
1
cos at +C
2
sin at, t R.
cu C
1
, C
2
constante arbitrare.
+ a
2
x = cos at, a R 0. Sa se gaseasca solut ia
problemei lui Cauchy cu condit iile init iale x
_
a
_
= 0, x
a
_
=
2a
.
R: Solut ia generala a ecuat iei omogene asociate este
x(t) = C
1
cos at +C
2
sin at, t R.
Cautam o solut ie particulara pentru ecuat ia neomogena sub forma
x
(t) = u
1
(t) cos at +u
2
(t) sin at, t R.
n care u
1
(t) si u
2
(t) verica sistemul
u
1
cos at +u
2
sin at = 0, au
1
sin at +au
2
cos at = cos at.
Rezulta
u
1
=
1
2a
sin 2at, u
2
=
1
2a
(1 + cos 2at).
De unde, pana la constante aditive arbitrare, obt inem
u
1
(t) =
1
4a
2
cos 2at, u
2
(t) =
1
2a
t +
1
4a
2
sin 2at.
Avem deci solut ia particulara
x
(t) =
1
4a
2
cos at +
1
2a
t sin at, t R.
Solut ia generala a ecuat iei date se scrie atunci
x(t) = C
1
cos at +C
2
sin at +
1
4a
2
cos at +
1
2a
t sin at, t R.
cu C
1
, C
2
constante arbitrare. Solut ia problemei lui Cauchy cu condit iile init iale x
_
a
_
=
0, x
a
_
=
2a
, cum C
1
=
1
4a
2
, C
2
= 0, este x(t) =
t
2a
sin at.
14.28 Sa se integreze urmatoarele ecuat ii stiind ca ecuat iile omogene corespunzatoare
admit solut iile indicate:
1) (2t + 1)x
+ 4tx
4x = (2t + 1)
2
, x
1
= t, x
2
= e
2t
.
2) (t
2
+ 1)x
2tx
+ 2x = 2(t
2
+ 1)e
t
, x
1
= t, x
2
= t
2
1.
3) tx
= x
tx
+x = t
2
, x
1
= t, x
2
= e
t
, x
3
= e
t
.
R: Avem:
1) x(t) = C
1
t +C
2
e
2t
+t
2
1
2
t +
1
4
.
2) x(t) = C
1
t +C
2
_
t
2
1
_
+ (t 1)
2
e
t
.
3) x(t) = C
1
t +C
2
e
t
+C
3
e
t
+t
2
+ 2.
+
2
t
x
+x = 0, daca x
1
(t) =
sin t
t
este o solut ie partic-
ulara.
R: Se face schimbarea de variabila dependenta x = x
1
y. Se obt ine:
x(t) =
1
t
(C
1
sin t +C
2
cos t).
14.30 Sa se integreze ecuat ia t
2
(ln t 1)x
tx
+x = 0, daca x
1
(t) = t este o solut ie
particular a.
R: x(t) = C
1
t C
2
ln t.
14.4 Ecuat ii de ordinul n cu coecient i constant i
14.31 Sa se gaseasc a solut iile generale ale ecuat iilor diferent iale liniare de ordinul al
doilea cu coecient i constant i:
1) x
5x
+ 6x = 0. 2) x
9x = 0. 3) x
= 0.
4) x
+x = 0. 5) x
2x
+ 2x = 0. 6) x
+ 4x
+ 13x = 0.
R: 1) Ecuat ia caracteristica r
2
5r + 6 = 0, are radacinile r
1
= 2, r
2
= 3. Solut ia
generala este x(t) = C
1
e
2t
+C
2
e
3t
. 2) x(t) = C
1
e
3t
+C
2
e
2t
. 3) x(t) = C
1
+C
2
e
t
.
4) x(t) = C
1
cos t+C
2
sin t. 5) x(t) = e
t
(C
1
cos t +C
2
sint). 6) x(t) = e
2t
(C
1
cos 3t+
C
2
sin 3t).
+x =
1
cos t
, t R k +

2
.
R: Ecuat ia omogena x
+ x = 0 are ecuat ia caracteristica r

2
+ 1 = 0, cu radacinile
r
1
= i, r
2
= i. Solut ia generala a ecuat iei omogene este deci
x(t) = C
1
cos t +C
2
sin t.
Cautam o solut ie particulara pentru ecuat ia neomogena sub forma
x
(t) = u
1
(t) cos t +u
2
(t) sin t,
cu u
1
cos t +u
2
sint = 0, u
1
sin t +u
2
cos t =
1
cos t
, de unde u
1
= tg t, u
2
= 1 si deci
u
1
(t) = ln [ cos t[, u
2
(t) = t,
ncat, solut ia generala a ecuat iei neomogene va
x(t) = C
1
cos t +C
2
sin t + cos t ln [ cos t[ +t sint.
14.33 Sa se gaseasca solut iile generale ale ecuat iilor diferent iale liniare cu coecient i
constant i de ordinul al doilea, neomogene:
1) 2x
x = 4te
2t
. 2) x
2x
+x = te
t
. 3) x
+x = t sin t.
4) x
+x = t
2
+t. 5) x
+x
= t 2. 6) x
x = te
2t
.
7) x
7x
+ 6x = sin t. 8) x
+ 4x = t sin 2t. 9) x
+ 3x
+ 2x = t sin t.
R: 1) Se cauta o solut ie particulara de forma: x
(t) = e
2t
(At +B). Se obt ine
x(t) = C
1
e
t
+C
2
e
t
2
+e
2t
_
4
5
t
28
25
_
.
2) Se cauta o solut ie particulara de forma: x
(t) = t
2
e
t
(At +B). Se obt ine
x(t) = (C
1
+C
2
t) e
t
+
1
6
t
3
e
t
.
3) Se cauta o solut ie particulara de forma: x
(t) = t[(At +B) cos t + (Ct +D) sin t].

Se obt ine
x(t) = C
1
cos t +C
2
sin t
t
2
4
cos t +
t
4
sin t.
4) x(t) = 2 +t +t
2
+C
1
cos t +C
2
sin t.
5) x(t) = C
1
+C
2
e
t
3t +
1
2
t
2
.
6) x(t) = C
1
e
t
+C
2
e
t
+
1
3
_
t
4
3
_
e
2t
.
7) x(t) = C
1
e
t
+C
2
e
6t
+
7
74
cos t +
5
74
sin t.
8) x(t) = C
1
cos 2t +C
2
sin 2t
1
8
t
2
cos 2t +
1
16
t sin 2t +
1
64
cos 2t.
9) x(t) = C
1
e
2t
+C
2
e
t
+
_
3
10
t +
17
50
_
cos t +
_
1
10
t +
3
25
_
sin t.
constant i de ordinul al doilea, neomogene:
1) x
+x
= 4t
2
e
t
. 2) x
+ 10x
+ 25x = 4e
5t
.
3) x
6x
+ 9x = 25e
t
sin t. 4) x
+ 2x
+ 5x = e
t
cos 2t.
R: Avem:
1) x(t) = C
1
+C
2
e
t
+
_
2t
2
6t + 7
_
e
t
.
2) x(t) = (C
1
+C
2
t) e
5t
+ 2t
2
e
5t
.
3) x(t) = C
1
e
3t
+C
2
e
3t
t + (4 cos t + 3 sin t) e
t
.
4) x(t) = C
1
e
t
cos 2t +C
2
e
t
sin 2t +
1
4
te
t
sin 2t.
constant i de ordin mai mare decat doi:
1) x
13x
+ 12x
= 0 2) x
+x = 0. 3) x
(4)
2x
= 0.
4) x
3x
+ 3x
x = 0. 5) x
(4)
+ 8x
+ 16x = 0. 6) x
(4)
2x
+x = 0.
7) x
2x
3x
= 0. 8) x
+ 2x
+x
= 0. 9) x
+ 4x
+ 13x
= 0.
R: Avem:
1) x(t) = C
1
+C
2
e
t
+C
3
e
12t
.
2) x(t) = C
1
e
t
+e
t
2
_
C
2
cos
3
2
t +C
3
sin
3
2
t
_
.
3) x(t) = C
1
+C
2
t +C
3
e
t
2
+C
4
e
t
2
.
4) x(t) = e
t
_
C
1
+C
2
t +C
3
t
2
_
.
5) x(t) = (C
1
+C
2
t) cos 2t + (C
3
+C
4
t) sin 2t.
6) x(t) = (C
1
+C
2
t) e
t
+ (C
3
+C
4
t) e
t
.
7) x(t) = C
1
+C
2
e
t
+C
3
e
3t
.
8) x(t) = C
1
+ (C
2
+C
3
t) e
t
.
9) x(t) = C
1
+ (C
2
cos 3t +C
3
sin 3t) e
2t
.
constant i:
1) x
+ 4x
+ 5x = 0. 2) x
(5)
2x
(4)
+ 2x
4x
+x
2x = 0.
3) x
(4)
+ 4x
+ 8x
+ 8x
+ 4x = 0. 4) x
(4)
4x
+ 5x
4x
+ 4x = 0.
R: Avem:
1) x(t) = (C
1
cos t +C
2
sin t) e
2t
.
2) x(t) = (C
1
+C
2
t) cos t + (C
3
+C
4
t) sin t +C
5
e
2t
.
3) x(t) = [(C
1
+C
2
t) cos t + (C
3
+C
4
t) sin t] e
t
.
4) x(t) = C
1
cos t +C
2
sin t + (C
3
+C
4
t) e
2t
.
14.37 Sa se gaseasc a solut ia generala a ecuat iei
x
(4)
+ 2x
+ 5x
+ 8x
+ 4x = 40e
t
+ cos t.
R: Ecuat ia caracteristica r
4
+ 2r
3
+ 5r
2
+ 8r + 4 = 0 are radacinile r
1
= r
2
= 1 si
r
3
= 2i, r
4
= 2i. Solut ia generala a ecuat iei omogene se scrie
x(t) = (C
1
+C
2
t)e
t
+C
3
cos 2t +C
4
sin 2t, t R.
Deoarece r = 1 este radacina dubla pentru ecuat ia caracteristica, vom cauta o solut ie
particulara de forma
x
(t) = At
2
e
t
+Bcos t +C sin t.
Introducand n ecuat ie si identicand coecient ii, se gaseste A = 4, B = 0, C =
1
6
si deci
solut ia generala a ecuat iei neomogene va
x(t) = (C
1
+C
2
t)e
t
+C
3
cos 2t +C
4
sin 2t + 4t
2
e
t
+
1
6
sin t, t R.
constant i de ordin mai mare decat doi, neomogene:
1) x
(4)
2x
+x
= e
t
. 2) x
(4)
2x
+x
= t
3
.
3) x
+x
x = t
2
+t. 4) x
= 12t
2
+ 6t.
R: 1) Se cauta x
(t) = At
2
e
t
. Rezulta x(t) = C
1
+C
2
t +
_
C
3
+C
4
t +
t
2
2
_
e
t
.
2) Se cauta x
(t) = t
2
_
A+Bt +Ct
2
+Dt
3
_
. Rezulta
x(t) = (C
1
+C
2
t) + (C
3
+C
4
t) e
t
+ 12t
2
+ 3t
3
+
1
2
t
4
+
1
20
t
5
.
3) x(t) = C
1
cos t +C
2
sin t +C
3
e
t
1 3t t
2
.
4) x(t) = C
1
+C
2
t +C
3
e
t
15t
2
5t
3
t
4
.
14.39 Sa se gaseasc a solut ia particulara a ecuat iei:
x
+ 2x
+ 2x
+x = t,
care verica condit iile init iale: x(0) = 0, x
(0) = 0, x
(0) = 0.
R: x(t) = e
t
+e
t
2
_
cos
3
2
t +
1
3
sin
3
2
t
_
+t 2.
14.5 Ecuat ia lui Euler
14.40 Sa se integreze ecuat iile Euler:
1) t
2
x
+tx
+x = 1. 2) t
2
x
+ 3tx
+x = 0.
3) t
2
x
4tx
+ 6x = t. 4) t
2
x
+ 2tx
6x = 0.
5) t
2
x
2tx
+ 2x = t
2
2t + 2. 6) t
2
x
tx
3x = t.
R: Avem:
1) x(t) = C
1
cos (ln t) +C
2
sin (ln t) + 1.
2) x(t) = (C
1
+C
2
ln t)
1
t
.
3) x(t) = C
1
t
3
+C
2
t
2
+
1
2
t.
4) x(t) = C
1
t
2
+C
2
1
t
3
.
5) x(t) = C
1
t +C
2
t
2
t
2
+ 2t ln t + 1 +t
2
ln t + 2t.
6) x(t) = C
1
1
t
+C
2
t
3
1
4
t.
14.41 Sa se integreze ecuat iile Euler:
1) (t 2)
2
x
3 (t 2) x
+ 4x = t 2.
2) t
3
x
t
2
x
+ 2tx
2x = t
3
+ 2t.
3) (4t 1)
2
x
2 (4t 1) x
+ 8x = 0.
4) (t + 1)
3
x
+ 3 (t + 1)
2
x
+ (t + 1) x = 6 ln (t + 1) .
R: Avem:
1) x(t) = t 2 + [C
1
+C
2
ln (t 2)] (t 2)
2
.
2) x(t) = C
1
t +C
2
t
2
+C
3
t ln t +
1
4
t
3
t
_
ln
2
t + 2 ln t + 2
_
.
3) x(t) = C
1
_
(4t 1) +C
2
(4t 1).
4) x(t) =
C
1
t+1
+
C
2
t+1
ln (t + 1) +
1
t+1
ln
3
(t + 1).
14.42 Sa se gaseasc a solut ia particulara a ecuat iei:
t
2
x
= tx
+x = 2t,
care verica condit iile init iale: x(1) = 0, x
(1) = 1.
R: x(t) = t
_
ln t + ln
2
t
_
.
Bibliograe
[1] Lia Aram a, T. Morozanu, Culegere de probleme de calcul diferent ial si integral,
Vol. I, Editura Tehnica, Bucuresti, 1967.
[2] V. Barbu, Ecuat ii diferent iale, Editura Junimea, Iasi, 1985.
[3] G. N. Berman, A Problem Book in Mathematical Analysis, Mir Publishers,
Moscow,1980.
[4] Gh. Bucur, E. C ampu, S. G ain a, Culegere de probleme de calcul diferent ial si
integral, Vol. II si III, Editura Tehnica, Bucuresti, 1967.
[5] I. Burdujan, Elemente de algebra liniara si geometrie analitica, Rotaprint IPI,
1982.
[6] N. Calistru, Gh. Ciobanu, Curs de analiza matematica, Rotaprint IPI, 1988.
[7] G. Chilov, Analyse mathematique,

Editions Mir, Moscou, 1984.
[8] S. Chirit a, Probleme de matematici superioare, Editura Didactica si pedagogica,
Bucuresti, 1989.
[9] A. Corduneanu, Ecuat ii diferent iale cu aplicat ii n electrotehnica, Editura FA-
CLA, Timisoara, 1981.
[10] A. Corduneanu, A. L. Pletea, Not iuni de teoria ecuat iilor diferent iale, Editura
MATRIX ROM, Bucuresti, 1999.
[11] B. Demidovich, Problems in mathematical analysis, Mir Publishers, Moscow, 1981.
[12] N. Donciu, D. Flondor, Analiza matematica. Culegere de probleme, Editura
ALL, Bucuresti, 1993.
[13] N. Gheorghiu, T. Precupanu, Analiza matematica, Editura Didactica si peda-
gogica, Bucuresti, 1979.
[14] M. Krasnov, A. Kiselev, G. Makarenko, E. Shihin, Mathematical Analysis
for Engineers, Vol. I and II, Mir Publishers, Mosvow, 1990.
[15] V. A. Kudryavtsev and B. P. Demidovich, A Brief Course of Higher Mathe-
matics, Mir Publishers, Moscow, 1978.
192
BIBLIOGRAFIE 193
[16] Gh. Moros anu, Ecuat ii diferent iale. Aplicat ii, Editura Academiei, Bucuresti, 1989.
[17] C. P. Nicolescu, Teste de analiza matematica, Editura Albatros, Bucuresti, 1984.
[18] M. Nicolescu, N. Dinculeanu, S. Marcus, Analiza matematica, Vol. I, Editura
Didactica si pedagogica, Bucuresti, 1966
[19] Gh. Procopiuc, Matematica, Univ. Tehnica Gh. Asachi Iasi, 1999.
[20] Gh. Procopiuc, Gh. Slabu, M. Ispas, Matematica, teorie si aplicat ii, Editura
Gh. Asachi Iasi, 2001.
[21] M. Ros culet, Analiz a matematica, Editura Didactica si pedagogica, Bucuresti,
1984.
[22] Ioan A. Rus, Paraschiva Pavel, Gh. Micula, B. B. Ionescu, Probleme de
ecuat ii diferent iale si cu derivate part iale, Editura Didactica si pedagogica, Bu-
curesti, 1982.
[23] A. A. Shestakov, A Course of Higher Mathematics, Mir Publishers, Moskow,
1990.
[24] Gh. Siretchi, Calcul diferent ial si integral, Vol. 1, Not iuni fundamentale, Ed. st.
si Encicl., Bucuresti, 1985.
[25] Gh. Siretchi, Calcul diferent ial si integral, Vol. 2, Exercit ii, Ed. St. si Encicl.,
Bucuresti, 1985.
[26] Rodica Tudorache, Culegere de probleme de analiza matematica, Vol. I, Calculul
diferent ial, Univ. Tehnica Gh. Asachi Iasi, 2000.
[27] Rodica Tudorache, Culegere de probleme de analiza matematica, Vol. II, Calculul
integral, Univ. Tehnica. Gh. Asachi Iasi, 2001.

Probleme de Analiza Matematica Si Ecuatii Diferentiale

Încărcat de

Informații document

Drepturi de autor

Formate disponibile

Partajați acest document

Partajați sau inserați document

Opțiuni de partajare

Vi se pare util acest document?

Este necorespunzător acest conținut?

Drepturi de autor:

Formate disponibile

Probleme de Analiza Matematica Si Ecuatii Diferentiale

Încărcat de

Drepturi de autor:

Formate disponibile

GHEORGHE PROCOPIUC

2, ) este o reuniune de mult imi din ,

. Daca b < 1 rezulta 1 b > 0 si atunci n N

, mult imea majorant ilor este

5, sup A = , 6) inf A = , max A = sup A = 1,

un sir descendent de segmente reale. Sa se

, atunci exista un numar x

. Asadar mult imea

este marginita superior (orice b

este marginita inferior (orice a

x 1, observand ca aceasta are un minim egal cu 0 n x = 0.

x, (0, 1). Deoarece f are n

are loc inegalitatea:

. Putem lua N() =

este un subsir al sirului (sin n)

Intr-adevar, din [x[

()[ d(x, y) si pentru

(x) se ajunge la metoda lui Newton.

()[ d(x, y), condit ia [

, R, numita seria lui Riemann sau seria armonica generalizata

este descrescator si deci seria lui

este convergenta pentru > 0.

este monoton descrescator la zero, iar

n care 0 < 1 este simplu convergenta.

) cu > 0 este monoton descrescator la zero. Dupa criteriul lui Leibniz

z. 2) f (x, y, z) = arcsin x + arcsin y + arcsin z.

[1, 3] pentru care [x x

Insa, pentru (x, y) (0, 0) avem lim

(x) = cos x xsin x. 4) f

(x) = 2 cos 2x.

R, denita prin f (x) = a

(x) = 0 are cel put in o solut ie n

(b) = 0. Sa se arate ca exista cel put in un punct c (a, b) a.. f

(d) = 0. Exista apoi c

Hospital. Se obt ine

1 +x, pe intervalul [0, 1], sa nu difere de f (x) cu mai

x este continua si f (4) = 2.

sin cos r cos cos r sin sin

sin cos cos sin

cos sin r sin sin r cos cos

+y = 4 cos [ln (1 +x)] , t = ln (1 +x) .

In punctul (2, 1),

Insa dx +dy = 0 si deci d

, x R cu > 0, este uniform

< 1 rezulta x (, 1) (1, +). Pentru x = 1 seria este

< 1 rezulta ca seria este convergenta pentru orice R pentru:

(x) = ln (1 +x), t inand seama de dezvoltarea funct iei ln (1 +x),

OA[[ = 2a si tangenta n A. O coarda variabila care

PQ (cissoida lui Diocles).

PQ (trisectoarea lui Mac Laurin).

OA, avem P(a cos 2, a sin 2),

(t) = a(1 cos t), y

(t) = a sint, ecuat ia tangentei: xsin t y(1 cos t) a(t

are ecuat ia:

(x, y) = 0. Se obt ine: y = a.

(t) = 0 pentru t = 1, x(1) = 2, y(1) = 3,

(t) = 0 pentru t = 0, x(0) = 0, y(0) = 0. 6. Ecuat ia implicita a curbei este:

(t) = 2r sin t(1 + 2 cos t), x

(t) = 2r(1 cos t)(1 + 2 cos t), y

. Ecuat iile proiect iilor pe planele de coordonate sunt: pe

cos , gasim reprezentarea parametrica: x = acos ,

(0) = a(i+j)bk, ecuat iile tangentei n M

(0) = 3, ecuat iile tangentei n M

= 3 sin t i = 3 cos t j +4k, ds = [[r